“微专题”教学在高三复习中的应用研究

钱春艳

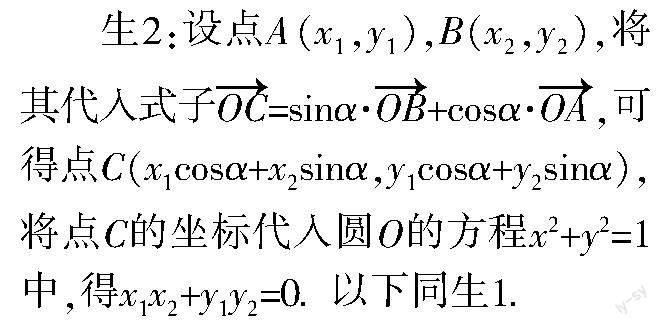
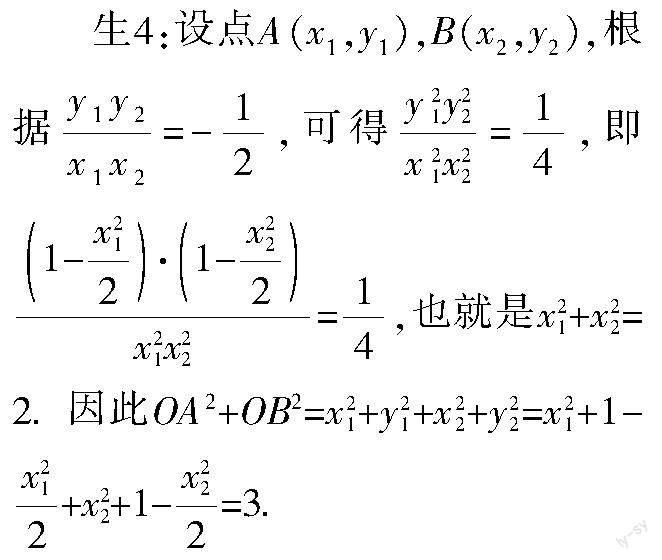
［摘  要］ “微专题”的特点是“小身材，大能量”，它能将一个知识点讲透彻、说明白. 文章从“微专题”教学的特征、“微专题”教学的必要性、“微专题”教学资源的开发措施以及“微专题”教学实践等方面展开分析，具体以“平面向量与解析几何的交汇题”的教学为例，引导学生逐个突破三个实际问题，由此获得相应的结论与推论，达到知识的融会贯通.

［关键词］ 微专题；交汇题；教学；思维

高考复习需经历知识梳理、专题突破与综合提升几个阶段，不论哪一轮复习都要在巩固“双基”的基础上，培养“真能力”［1］. 为了让学生更好地掌握各个专题知识，教师可以将学生接触过的各个知识点“集零为整”，通过若干个“微专题”引导学生逐一突破知识障碍，帮助学生建立系统化的知识结构.

机缘巧合，笔者有幸参加了一堂“微专题”研讨课，颇受启发，之后便对“微专题”教学展开了一系列研究，收效颇丰.

“微专题”教学的特征

1. “微”在教学内容上

所谓的“微专题”教学是指教师在既定的主题下组织的一种教学活动，这种教学活动主要将“火力”集中在解决一类问题或一个知识点上，属于“小切口”的教学模式. 因此，“微专题”教学的内容少，但挖得深，易暴露知识本质.

“微专题”教学强调“以生为本”的理念，要求教学必须结合学生的实际认知水平，从学生的真正需求出发，结合学生的实际情况对一个个小问题加以提炼总结，最后串珠成链形成学生真正需要的教学内容［2］. 从教学策略来看，教学内容的多少并不重要，重要的是采取怎样的教学方法，如何将一个个零散的知识点组成有法可依、有据可循的整体.

2. “微”在教学形式上

“微专题”教学中的“微”是形式，其本质是“专”. “微专题”设计的关键在于确定有价值的教学主题，这可以从知识点的诞生、考点的细化、易错点的辨析以及思维的拐角处和重难点的突破口出发，根据学生的实际内在需求选择或建构有价值的“微专题”主题.

“小切口、高针对性”是“微专题”教学的主要特征，该特征是促使深度学习真实发生的基础，学生在这种独特的教学活动中往往能建构清晰的知识网络，形成系统研究问题的方法，从而深化对各个知识点的理解，提升数学综合素养.

“微专题”教学的必要性

在高三复习阶段，学生面临着升学压力，很容易对旧知产生“疲劳感”，在一轮又一轮的测试中，不少学生的学习热情与学习效果都大打折扣. 调查发现，一些认知水平处于中等的学生，在复习过程中会产生一种力不从心之感，尤其遇到综合程度较高的问题，常常会因为其中一个知识点的遗忘，而出现解题错误的现象，这些都严重消减了学生的复习热情，让复习教学难上加难.

研究发现，“微专题”教学能有效激发学生的复习热情，让学生积极主动地参与到复习中来，为建构完整的认知结构做铺垫；能有效消减学生心理上的负担，让学生在课堂中获得学习成就感. 久而久之，学生会再次建立学习信心.

结合高考考纲要求与学生的实际情况，适当地为学生量身定制一些“微专题”课程，可以催生学生的探索思维及新鲜感. 随着一个个小问题的解决，不仅能提升学生的复习效率以及应试的精准度，还能促进学生创新意识的发展. 因此，在新课标的引领下，“微专题”教学的实施值得推广.

“微专题”教学资源的开发措施

作为一线的高三数学教师，应拥有敏锐的观察力，要善于捕捉教学过程中的一些优质素材. 尤其是对待课堂中动态生成的问题，应做个有心人，保持高度敏感的状态，因为灵感常源于动态的生成、思考与钻研［3］. 从某种意义上来说，“微专题”就是某个独立问题或一类问题的强化与突破，抑或是某类新问题的深入探索.

笔者参与的“微專题”研讨活动在高三二模考试后，结合学生在二模考试中的实际情况，笔者做了一定的统计，发现不少学生对“设而不求”“整体代入”的应用意识不强，尤其在“平面向量与解析几何交汇题”的求解中. 交流发现，即使做对的学生，对“平面向量与解析几何交汇题”的思考也不够深入，一些学生认为这个内容与之前接触过的“平面向量与椭圆交汇问题”似乎有些联系，但又无法表达清楚.

基于这种背景，笔者决定围绕“平面向量与解析几何交汇题”这个主题，设计一堂“微专题”复习课.

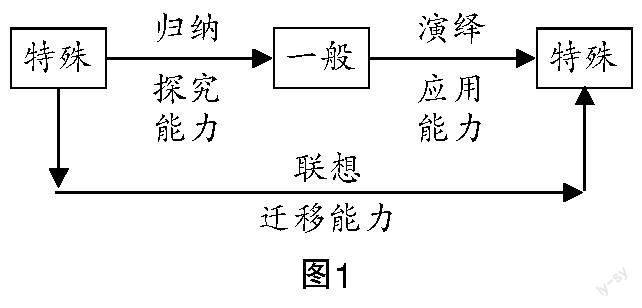
研究发现，将此类问题迁移到基本圆中，更符合学生的一般认知规律. 为此，本节课教学可以“圆中的平面向量问题”作为切入口. 为了让本节课取得预期的教学效果，笔者设计了教学初稿，并与两位同事交流，尽可能完善教学预设，以期获得较好的教学效果. 图1为本节课的立意及构思.

“微专题”教学实践

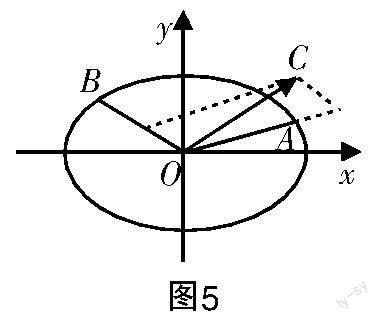
问题1 如图2所示，在平面直角坐标系xOy中，如果圆O：x2+y2=1和直

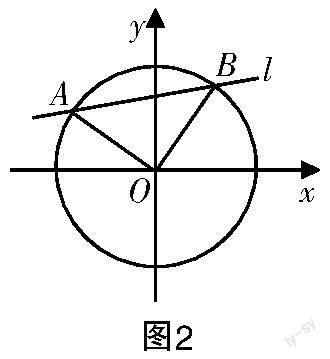
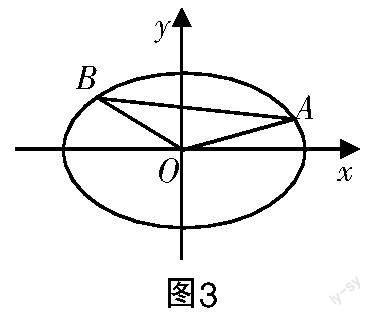
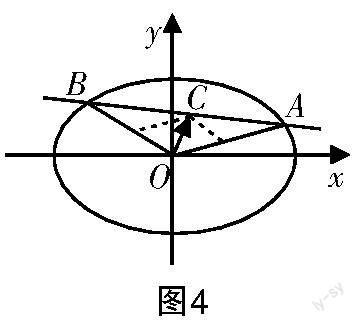
问题2 如图3所示，在平面直角坐标系xOy中，若点A，B位于椭圆+y2=1上，但非顶点，已知OA的斜率与OB的斜率之积为-.

证明：（1）OA2+OB2恒为定值；

（2）线段AB的中点C必然位于某定椭圆上.

1. 问题1的教学过程

笔者给予学生充足的时间，鼓励学生独立思考问题1，并邀请学生到讲台上投影结论，讲解求解过程，与大家分享求解思路.

师：非常好！当我们在处理问题的过程中，遇到直线和圆的问题时，可借助数形结合思想，通过一定的方法简化运算. 接下来，我们再看另外一位同学的解题过程（投影），请该生跟大家分享一下解题思路.

这两位学生的解题方法比较典型，他们从不同的角度展示了“将向量式转化成数量式”的不同途径：①构造向量数量积进行运算；②结合坐标相等进行运算. 这种主攻单个问题的教学方式，让原本解题思路处于模糊状态的学生，在同伴的解说与两种解题方法的类比下，对此类问题有了直观印象以及更加深刻的认识.

2. 问题2（1）的教学过程

笔者同样给予充足的时间供学生自主思考、解题，要求学生写清楚解题过程. 学生解题时，笔者加强巡视，及时发现学生思维的卡壳点，为接下来的教学提供方向. 学生解题完成后，笔者和学生开始如下互动.

师：大家基本都解完了本题，现在哪位同学来说说你的解题过程？

师：听起来不错，在此过程中你用了“同理”二字，这个词用得妙，能跟我们说说用“同理”二字基于什么目的吗？

生3：就是为了减少没必要的重复运算.

师：不错！若想最大程度减少运算量，“同理”在什么时候用比较合理呢？

师：很棒！确实，这里想要简化运算过程，那么“同理”用在最后一步比用在中间一步更合适. 还有不同的解题方法吗？

师：这种方法有点意思，显然回避了分别求点A，B坐标的过程——那是一个异常烦琐的过程. 这种“设而不求”的解题方法是解析几何中重要的求解技巧，值得我们关注.

一石激起千层浪，这个问题成功点燃了学生思维的火花，有学生立即回应x+x=a2，y+y=b2，OA2+OB2=a2+b2. 由此可见，以上互动为学生带来了不少启示. 学生在后续学习中，若遇到类似问题则能从不同角度去思考、分析并解题，这也是“微专题”教学的主要目的所在.

2. 问题2（2）的教学过程

依然先由学生自主探索解题，解题完成后与笔者共同探讨解题方法，以汲取或分享解题优点，不断优化解题思维.

师：哪位同学来展示一下问题2（2）的求解过程？

生5：从式子的结构特征出发，若想将五个式子都用上，同时消去x，x，y，y，则需要建立关于x，y的等量关系.

师：这种方法，从本质上来看，就是用消参法来探索轨迹方程. 除此之外，大家还有其他方法吗？

师：非常好！这位同学灵活地将待定系数法应用到此处，值得赞扬. （其他学生自发地为生6鼓掌）

为了引发学生更加深入地思考，笔者要求学生以小组合作学习的模式思考以下几个问题：①如果点C是线段AB上靠近点A的三等分点呢？②如果点C是直线AB上的任意一点呢？③如果点C是平面上的任意一点呢？

随着问题的提出，学生进入了合作交流的状態，并科学严谨地证明自己的猜想，进而获得了以下结论.

推论2：若点C位于椭圆E上，则λ2+μ2=1.

结合以上结论和推论，再回过头来求解本节课的初始问题，就异常简单了. 为了让学生彻底搞清楚这一类问题的求解技巧与知识本质，教师应着重强调以上结论和推论并非唯一的解题途径，遇到实际问题时，应根据实际情况进行分析，只有从根本上掌握了解题方法，才能“以不变应万变”.

总之，“微专题”教学能有效提高高三复习效率，是值得推广的一种复习教学方式. “微专题”课程的切入口宜小，着重凸显“微”字，以问题作为“微专题”主题不乏是一种有效的手段. 同时，“微专题”的教学方式与内容须足够精准且有内涵，教学过程中要凸显数学独有的思想方法，让学生从真正意义上掌握问题的本质，从而提升学生的解题能力.

参考文献：

［1］ 曹才翰，章建跃.数学教育心理学［M］. 北京：北京师范大学出版社，2006.

［2］ 涂荣豹. 数学教学认识论［M］. 南京：南京师范大学出版社，2003.

［3］ 史宁中.试论数学推理过程的逻辑性——兼论什么是有逻辑的推理［J］.数学教育学报，2016，25（04）：1-16+46.