基于前置 重置路径 通透本质
莫与谈
















[摘 要] “长方形和正方形的面积”是小学数学的重难点内容之一,在教学探究中,学生常常在教师的指导下按部就班地“摆”小正方形,“为了摆而摆”,导致学生“知其然而不知其所以然”,陷入重公式记忆、弃本质理解的怪圈。教师多是关注学生对面积公式的熟练运用,忽视面积意义的教学,导致部分学生不能真正理解长方形的面积计算的原理。研究者基于前置性学情诊断,深层次了解学生的认知差异,聚焦“长方形面积计算的本质”,重新设置教学路径:暴露发现与困惑,引发思考;结合探究,追寻本质;操作验证,通透本质;探析特殊,沟通关联;巩固练习,灵活运用。学生经历了知识的建构过程,认知结构得以丰盈,促进了空间思维的发展和数学思维水平的提升。
[关键词] 前置性探究作业;长方形的面积;教学思考;教学实践
一、课前思考
“长方形和正方形的面积”是“图形与几何”领域的重要内容,是学生第一次学习图形的面积。学生从学习长度到学习面积,是其空间思维发展史上的一次重大飞跃。学习好该内容,不仅有利于学生空间观念的发展,也为以后学习其他平面图形的面积奠定了基础。长方形面积的本质在于度量,即通过面积单位的计数,实现对图形大小的定量刻画[1]。然而在以往的教学中,学生常常在教师的指导下按部就班地“摆”小正方形,“為了摆而摆”,导致学生“知其然而不知其所以然”,陷入重公式记忆、弃本质理解的怪圈。教师多是关注学生面积公式的熟练运用情况,忽视面积意义的教学,导致部分学生不能真正理解长方形的面积计算的原理。教师在教学“长方形和正方形的面积”时,不能只关注公式的记忆和面积的计算,更要重视引导学生充分经历学习过程,让学生在过程中加深理解、提升能力、发展深度思维[2]。
事实上,学生在学习这一内容时需要经历“数面积单位的个数”到“面积单位的总数=每行的面积单位个数×行数”,在此基础上提炼出“长方宽的面积=长×宽”,即“计数—模型—公式”这三个层次。人教版小学数学教材提供的学习路径是:
①两名学生以不同的方式用面积单位去测量长方形的面积,呈现了两种方法:一是一个一个地数的方法,这是学生最本能的方法;二是用乘法计算出面积单位的个数,这一方法为面积公式的形成奠定了基础,并以“聪聪”的提问引出后面的学习。
②用面积单位拼摆多个长方形,并用表格记录长、宽和面积,探索它们之间的关系,从而概括出长方形的面积公式。
③先测量两个图形的长和宽,然后用面积公式分别计算它们的面积,将正方形看作特殊的长方形,从而通过推理概括出正方形的面积公式。
二、前置性探究学习与分析
以上是研究团队对教学现象的观察和对教材的理解,如何才能在教学中更好地关注到学生现有的认知水平,如何让学生通过度量的本质深层次地理解长方形的面积计算?在教学这一内容时,研究团队设计了前置性探究作业(见图1),以期了解学生现有的认知水平。
2. 前置性探究作业分析
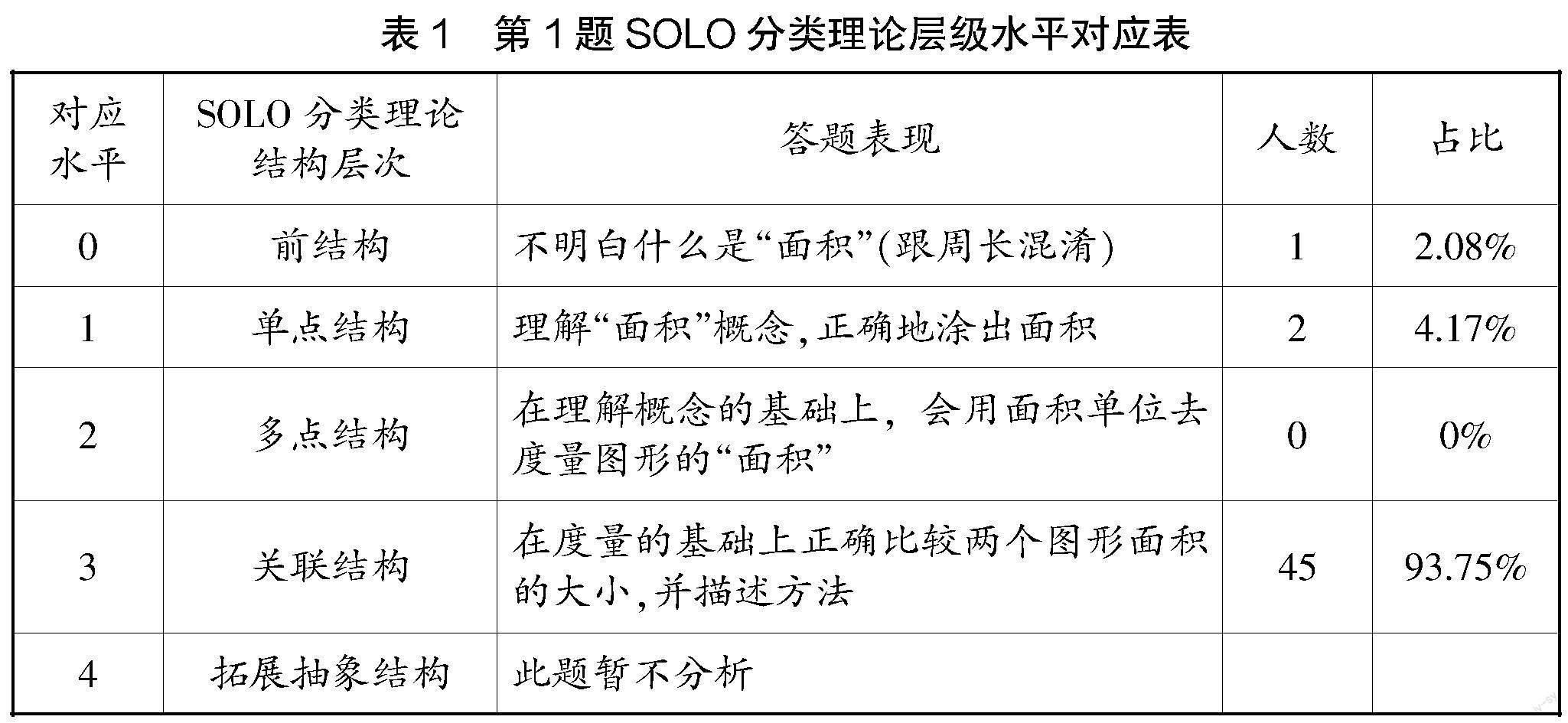
研究团队结合“SOLO分类理论”对三年级某班共48人布置了前置性探究作业,并记录他们的探究过程与探究结果。
从学生前置性作业各层级水平结果来看(见表1),该班学生基本都能正确地用彩笔或阴影涂出A、B两个图形的面积,并且都能想到利用教师提供的学具(1平方厘米的小正方形)。学生通过摆小正方形来度量两个图形的面积,根据面积单位的个数来判断两个图形面积的大小。从前置性作业来看,该班学生对“面积”概念的掌握较好,会用面积单位去度量图形的大小,这些知识储备为后面的探究打下了良好的基础。
从前置性作业探究结果来看(见表2),该班约90%的学生在教师提供学具及给出提示的情况下,能用多种方式探究长方形的面积,约50%的学生能通过多种途径得出长方形面积的计算公式。当然学生可能并不知道该公式的具体意义,只是通过数小正方形个数的方式得到。仅5名同学能基本弄清长方形面积公式的由来,因此本节课的落脚点是让学生真正明白长方形计算公式的由来。
三、教学实践
研究团队基于对教材的分析和前置性学情诊断,深层次了解了学生的认知差异,聚焦“长方形面积计算的本质”,课堂实践中借助学生前置性探究作业作品,进行了合理设计,重新设置教学路径。
1. 暴露发现与困惑,引发思考
师:前面我们已经通过摆一摆对长方形的面积进行了探究,我们来看看大家有哪些收获与困惑(课件出示图2、图3、图4、图5)。
设计意图:开门见山,紧密联系前置性探究学习,将学生的发现与困惑暴露出来,引发学生的思考,为学习新知做好准备。
今天我们将在此基础上继续进行探究(板书课题)。
2. 结合探究,追寻本质
(1)结合前置性探究1,感悟度量本质
(课件出示图6和图7)
师:这两幅作品中,哪幅图是表示图形的面积?说说你的想法。
生1:因为第一个图是描了图形一周的长度,这是它的周长。面积指的是图形表面的大小,所以第二个图才是表示它的面积。
师:这两个图形的面积谁大?说说你们是怎样比较的?
生2:第一个图的面积大,第一个图是7平方厘米,第二个图是6平方厘米,第一个图比第二个图的面积大。
师:你是怎么知道第一个图的面积是7平方厘米的?
生2:因为第一个图一共可以摆7个小正方形,每个小正方形的面积是1平方厘米,所以是7平方厘米(课件出示图8)。
师:也就是说,这个图包括了7个1平方厘米的小正方形,它的面积就是7平方厘米。
设计意图:通过学生的辨析与讲解,厘清面积与周长的区别,让学生进一步明确什么是面积。比较两个图形的大小,让学生用面积单位去度量,并在铺摆图形的过程中理解:一个图形的面积的大小,就看它能铺摆多少个这样的面积单位。这样的度量活动能为学生接下来深入探究长方形的面积及理解面积的本质做好铺垫。
(2)结合前置性探究2,追寻面积本质
①“计数”面积单位
(课件出示前置性探究2)
师:同学们在昨天的探究中,找到了很多求长方形面积的方法,我们一起来看看他们是怎么思考的吧(图9)。
师:一共摆了几个面积单位?说说你们是怎么想的?
生3:一个个数出来的,一个图形里有几个1平方厘米,它的面积就是几平方厘米。
生4:可以列乘法算式,第一个长方形摆了2行,每行有3个,列式3×2=6,有6个1平方厘米,也就是6平方厘米。
师:说得很好,我们只需要知道每行的个数和行数就能计算出面积单位的个数,也就是长方形的面积。
②建立模型,感知本质
师:这位同学后面3个长方形并没有摆完,怎么可以知道它们的面积?(课件出示图10)
生5:想象这些图形中间是摆满了的,第2个长方形每行摆4个,摆3行,4×3=12,面积是12平方厘米。
生6:第3个长方形每行摆6个,摆4行,6×4=24,面积是24平方厘米。
生7:第4个长方形每行摆9个,摆6行,9×6=54,面积是54平方厘米。
师:看来,用“每行的个数×行数”可以算出长方形面积单位的个数,也就是长方形的面积。(板书:长方形中面积单位的个数=每行的个数×行数)
师:你能读懂这位同学的想法吗?(课件出示图11)
生8:我用“每行的个数×行数”,直接列乘法算式算出長方形的面积。
师:这位同学没有再摆小正方形了,他是怎么计算面积的 ?(出示图12)
生9:用尺子量出长方形的长和宽,直接用长×宽算出它的面积。
生10:相当于想象摆满了小正方形,用“每行的个数×行数”直接可以算出来。
③沟通联系,直逼本质
师:我们前面探究这些长方形的面积,无论是摆满了小正方形或只摆了其中的一部分,还是没有摆小正方形,只要尺子量出长方形的长和宽,都能列式算出它们的面积,我们解决的过程有什么相同的地方?
生11:都是用“每行的个数×行数”直接算出来的。
生12:用长方形的长和宽直接相乘就能得到它的面积。
师:为什么长乘宽就是长方形的面积呢?
生13:长就相当于每行摆几个小正方形,宽相当于摆几列,所以长乘宽就是长方形的面积。
师:说得很清楚!是这样吗?长9厘米,对应每行摆了9个,宽6厘米对应着能摆这样的6行。现在,同学们来看看,这个长方形的面积可以怎样计算呢?
生14:9×6=54(平方厘米)。
生15:长×宽=面积。
(板书:长×宽=面积?)
设计意图:展示回顾学生不同思维层级的多种探究方法,从铺满到没有铺满,再到空白(测量长和宽),层层递进,学生经历了“计数面积单位”和建立“每行个数×行数”的面积模型的过程,引导学生发现长、宽与每行个数、行数及长方形内面积单位的个数和与长方形面积之间的关系,追根溯源寻求长方形面积公式的本质,长方形面积公式的推导有理有据。
3. 操作验证,通透本质
师:那是不是所有长方形的面积都可以用长×宽来计算呢?我们一起来验证。(出示小组合作探究要求,如表3)拼完之后,看看有什么发现?
学生进行操作验证和汇报交流。
学生在汇报交流中进一步明确:长就相当于每行摆几个小正方形,宽相当于摆几行,长方形中小正方形的个数就是长方形的面积,所以长乘宽就是长方形的面积。学生在操作验证与汇报交流中进一步掌握了长方形面积公式的本质。
设计意图:通过让学生自己动手摆出长方形,并通过大量的例子丰富学生的感性认知,实现从直观操作向表象操作、最后到模型操作的过渡[3],让学生深层次领悟长方形面积公式;同时在其中渗透数学严谨性的特点,让学生在操作验证中深刻理解长方形面积公式的本质。
4. 探析特殊,沟通关联
师:通过大家的研究,我们知道长乘宽可以计算长方形的面积(擦掉公式后面的问号)。现在我们学习了长方形的面积计算方法,那要求这两个长方形的面积还需要像刚才那样一个一个摆吗?那要知道什么条件?
生16:要量出它们的长和宽。
师:(课件出示图形的长和宽,如图13)第一个图形的面积是多少?
生17:8×6=48(平方厘米)。
师:为什么只要量出长方形的长和宽,就可以求出它的面积?
生18:长表示“每行的个数”,宽表示“摆的行数”,长乘宽能算出“摆的正方形个数”,也就是它的面积。
师:第2个图形的长和宽分别是多少?你们有什么想说的?
生19:长是6cm,宽是6cm,这是一个正方形,它的边长是6cm。
师:大家想想正方形的面积应该怎么计算?
生20:正方形的面积=边长×边长。
设计意图:当学生知道要求出长方形的面积,要先知道它的长和宽,在学生求出面积后,教师及时追问“为什么只要量出长方形的长和宽,就可以求出它的面积”,再次直击长方形面积的本质。教师在对比中引导学生进行知识迁移,让学生自主发现正方形的面积计算公式。
5. 巩固练习,灵活运用
师:刚才,大家通过自己的动手动脑,找到了长方形、正方形的面积计算方法。
师:我们再来回顾一下刚才的过程,我们是怎样找到长方形和正方形的面积计算方法。现在我们要挑战一个有难度的题,大家有信心吗?老师家里有一块长方形的地毯,如图14,其中每块彩色正方形的面积是1平方分米,你能算出这块地毯的面积吗?
设计意图:在学生获得知识后要及时运用,举一反三,加深理解,有助于学生对面积本质理解的进一步深化,培养学生推理、归纳和灵活运用的能力。
本节课结合学生的前置性探究作品,在理解教材编写意图的基础上,通过对学生前置性探究的诊断,重新设计教学路径,把握教学的本质;同时把学生的前置性探究作品融入课堂教学环境,使得课堂更具有亲和力,重难点教学更加突出,将量感、空间思维能力等数学核心素养培养落到了实处。学生经历知识的建构过程,深度理解“长方形面积计算的本质”,认知结构得以丰盈,促进了空间思维的发展和数学思维水平的提升,凸显了前置性探究教学的价值。
参考文献:
[1] 牛献礼. 把握度量本质,促成深度理解——《长方形的面积》教学与思考[J]. 教育视界,2022(05):43-45.
[2] 孙鸿雁. “长方形和正方形面积的计算”课例解读[J]. 中小学数学(小学版),2022(Z1):61-63.
[3] 褚明月. 突出比较,促进学生深度学习——以“长方形和正方形的面积”教学为例[J]. 小学数学教育,2020(22):12-13.

