五轴联动数控刀具切削加工误差非线性插补方法研究

王 颖

(陕西工业职业技术学院,陕西 咸阳 712000)

五轴联动数控刀具是制造业领域中一种高精度、高效率的加工刀具,在众多应用领域得到广泛应用。在高精度切削加工过程中,五轴联动数控机床摆心与刀具之间的运动轨迹误差会影响加工精度,此外机床还会受到多种因素的影响,如变形、振动等,这些因素都可能对机床刀具的切削加工精度产生影响。为此学者纷纷对如何实现机床刀具的误差插补进行研究,以提高机床切削加工的精度。

赵恒等[1]构建了刀轴偏差角模型,将加工坐标系与球面坐标系结合,获取两个坐标系的刀轴经纬度差异以及偏差角,通过优化相邻刀轴矢量的平均纬度,并改变工件装夹姿态,减少曲面侧铣加工误差,从而达到误差非线性插补的目的。该方法能够很好地实现误差插补,但插补后刀具轨迹与理想轨迹相差较大,整体插补效果较差。王圣斌等[2]利用插补器采集的信号构建前馈控制模型,基于最小二乘法设计对称滤波器,利用该对称滤波器抵消相应误差,并消除噪声干扰,实现误差插补。该方法具有较好的插补性能,但插补后误差仍然较大。何春茂等[3]基于最小二乘法构建误差插补数学模型,基于该模型结合激光干涉仪器获取设备的误差数据,最后通过周期插补坐标值的方式实现误差插补。该方法具有较高的补偿精度,但整体插补效果较差。

为了解决上述问题,本文提出五轴联动数控刀具切削加工误差非线性插补方法。非线性插补技术是一种高效且具有强实时性的误差插补方法。通过计算刀轴控制点的距离偏移值和角度变化,对刀位、刀闸位置进行调整和线性补偿,以确保刀具轨迹与理想轨迹保持一致,实现精确的切削加工。

1 五轴联动数控刀具切削加工误差非线性插补

1.1 误差产生原因分析

在制造业发达的现代,数控机床的进给系统已经较为完善,本文利用传递函数模型分析五轴联动数控刀具。

在五轴联动数控机床中,其单一轴在稳态下运行时,实际位置与指令位置会出现一个差值f,通常可将该差值视作系统跟随误差[4],f的大小与传动轴的运行速度w有关,计算公式为:

(1)

式中:Lqq为各轴位置环增益,其是系统速度变化的直接反映。

通过式(1)可知:在五轴联动数控刀具切削加工时,刀具旋转轴在两刀位点之间不断运动[5],由于刀具旋转轴的运行速度和实际刀轴矢量之间存在不对称差异,这种不对称差异会导致刀具轨迹形成误差,进而影响切削加工的精度。

1.1.1理想刀轴矢量计算

为了精准获取刀具处于最优位置时的理想刀轴矢量[6],通过计算两个刀位点之间的刀位偏移量来确定其夹角。理想刀轴矢量计算原理如图1所示。

图1 理想刀轴矢量计算原理图

将刀轴的初始矢量状态Ut在V轴上显示,矢量积(Ut×Uf)在W轴上显示,通过右手定则构建P′-VWA坐标系。利用刀轴的初始及末端位置组成的平面对刀轴偏向角β展开计算,以求取理想刀轴矢量。具体过程如下:

将初始矢量状态Ut到运行矢量状态Uf消耗的时间记作1个时间单位,两状态下的夹角记作β,β=arccos(Ut×Uf)。由此可以获取u时刻偏转角度βu:

βu=βgu0≤u≤1

(2)

式中:g为角变化率。在该时刻,位于P′-VWA坐标系中的刀轴矢量DP′可以表示为:

DP′(XP′,YP′,QP′)=(cosβu,0,sinβu)

(3)

式中:(XP′、YP′、QP′)为刀具的末端位置。

由此获得P-XYZ坐标系上刀轴矢量DP的计算式:

DP=DP′·U(V,W,A)=(V·cosβu,0,A·sinβu)

(4)

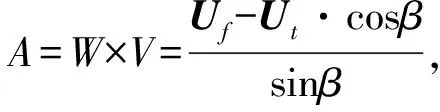
0≤u≤1

(5)

1.1.2实际刀轴矢量误差计算

通过计算两个旋转轴的运动角度(θ,γ),可以得到刀轴矢量的实际角度,具体计算方法如下:

(6)

式中:(Xf,Yf,Zf)为P-XYZ坐标系下刀具对应的偏移矢量。

假定Ut记作(0,0,1),当理想刀轴矢量由Ut变为Uf时,便表示该刀具的运动角度由(θt,γt)转变至(θf,γf),由此可以计算得到其运动角度:

(7)

获取u时刻刀具经过旋转轴的角度值[7]:

(8)

刀具在旋转轴u时刻,其运动角度(θu,γu)计算结果如下:

(9)

根据获取的运动角度(θu,γu),计算刀具在u时刻的实际刀轴矢量D(u):

(10)

式中:(Xu,Yu,Zu)为刀具在u时刻的末端位置。

1.1.3误差计算

五轴联动数控刀具的切削轨迹真实结果与理想结果的误差由机床摆心的运动轨迹决定。机床摆心g(u)的计算结果如下:

g(u)=M·D(u)+[Qf+Qt·(1-u)]

(11)

式中:M为机床摆心与刀位点的距离,Qt与Qf分别为运动初始及末端的刀位点。将理想刀轴矢量Dp(u)、实际刀轴矢量D(u)与公式(11)相结合,获取机床摆心g(u)在u时刻的理想位置gp(u)与实际位置g(u)的误差φ(u)[8]:

(12)

由此可以获取五轴联动数控刀具切削加工时产生的偏移误差,根据偏移误差开展非线性插补操作。

1.2 非线性插补方法设计

通过1.1节可以看出,五轴联动数控刀具切削加工时刀具运行轨迹与预期轨迹有一定偏差,从而影响加工精度。采用非线性插补方法对这些误差进行补偿,以保证后期加工精度。

刀具运动示意图如图2所示。图中,s(u)代表待加工零件的表面曲线。在加工该零件时,刀位与刀闸矢量坐标分别为sq(qx,qy,qz)和v(vx,vy,vz),刀轴控制点与刀尖的距离记作ζ。刀轴控制点对应的位置矢量sn(nx,ny,nz)用下式表述:

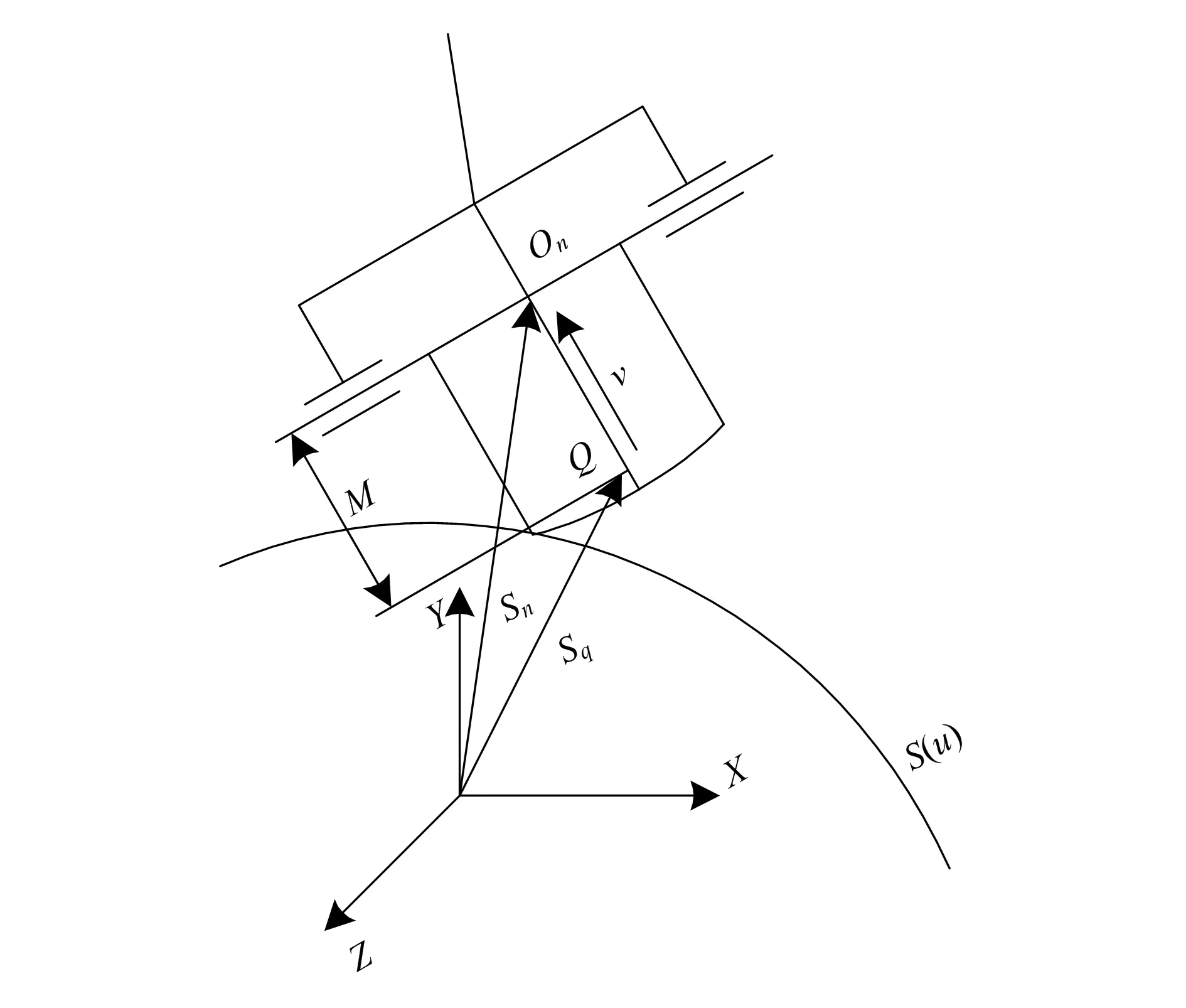
图2 刀具运动示意图

sn=φ(u)ζ·v/sq

(13)

当刀轴控制点从当前位置sn0(nx0,ny0,nz0)移动到sn1(nx1,ny1,nz1)时,距离偏移值Δs为:

Δs=Δsq+ζ·Δv(sn1-sn0)

(14)

式中:Δsq为刀位距离偏移值,Δv为刀闸距离偏移值。

在五轴联动数控刀具切削加工过程中,刀具每运动一次,便需要对其位移偏差作出补偿,以达到使刀尖轨迹始终保持与理想轨迹吻合的目的。

将刀轴控制点在X、Y、Z方向上的线性补偿位移记作[9-10]:Δn=Δsζ[(nx1-nx0)2+(ny1-ny0)2+(nz1-nz0)2]1/2。

在五轴联动数控刀具线性补偿位移的基础上,3个轴误差插补量为:

(15)

式中:θB0与θB1分别代表刀具沿X轴转动前后的角度变化,θC0与θC1分别代表刀具绕Y轴摆动前后的角度变化。通过上述计算可以完成对五轴联动数控刀具运行轨迹的位移补偿,实现五轴联动数控刀具切削加工误差的插补。

2 实验与分析

为了验证五轴联动数控刀具切削加工误差非线性插补方法的有效性,进行实验测试。实验现场如图3所示。

图3 实验现场

实验环境:使用五轴联动数控刀具加工机床,采用刀头半径为1 mm的球头铣刀。工件材料为6061-T6铝合金板,尺寸为200 mm×200 mm×30 mm。实验参数:切削速度为1 000 m/min,进给速度为100 mm/min,刀具转速为10 000 r/min。X、Y、Z轴切削距离传感器采样频率为100 Hz。A、B两轴切削距离传感器采样频率为50 Hz。切削液采用水溶性铣削冷却液。

通过比较插补前后机床刀具运行轨迹以及轨迹误差,来评估误差插补效果。通过式(9)、(12)获取刀具的运行轨迹,以及相应的刀具轨迹误差。

2.1 插补前后刀具运行轨迹对比

在实验环境相同的情况下,分别利用本文方法和文献[1]、文献[2]和文献[3]方法对同一五轴联动数控刀具实施误差控制,记录其插补前后的刀具运动轨迹,并与理想轨迹对比,结果如图4所示。

由图4可知,经过各方法的误差插补处理后,刀具整体运行轨迹较插补前均有适当优化,但与理想轨迹相比,仍存在一定的偏差。其中文献[3]方法的刀具轨迹与理想轨迹差别最大,文献[1]和文献[2]方法虽优于文献[3]方法,但明显差于本文方法。本文方法的刀具运行轨迹与理想轨迹贴合度最高,表明利用本文方法开展的五轴联动数控刀具轨迹误差插补效果好。

2.2 插补周期误差对比

在五轴联动数控刀具加工过程中,为实现高精度加工,需要将刀具误差控制在0～25 μm内。本实验中机床误差插补前,五轴联动数控刀具的误差最高可达38 μm。在实验环境相同的情况下,分别利用本文方法和文献[1]、文献[2]和文献[3]方法对该刀具展开误差控制操作,记录10个周期内的误差情况,得到的结果如图5所示。

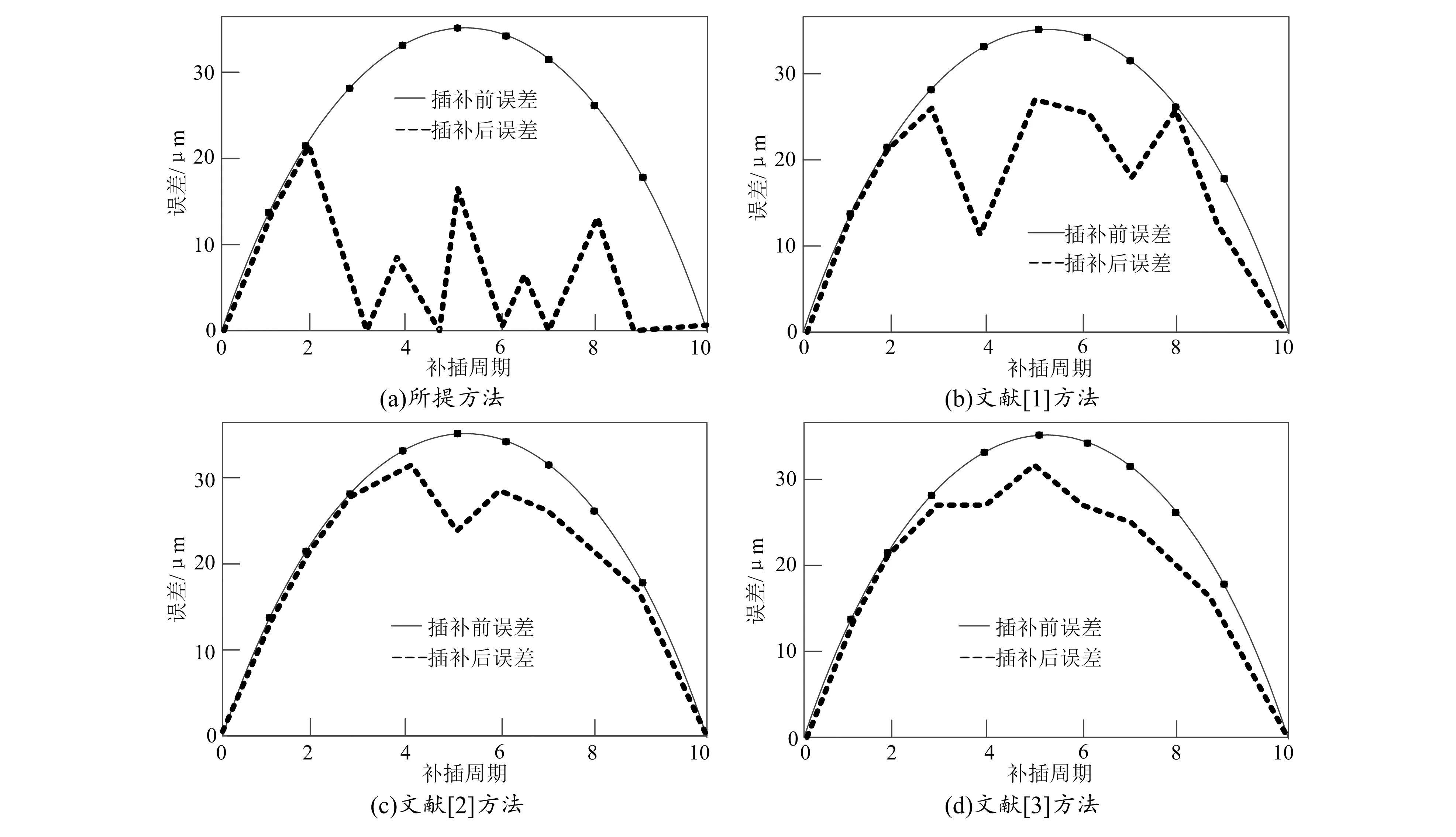
图5 各方法插补前后误差对比

由图5可知,在开展误差插补前,五轴联动数控刀具切削加工的误差呈现先增加后下降的趋势;在利用不同方法开展误差插补后,文献[2]和文献[3]方法下的误差随着插补周期的增加,呈先增加后下降的趋势,最大误差为30 μm,整体误差与插补前相差不大;文献[1]方法下的误差波动较大,最大误差为28 μm,其整体误差插补效果优于文献[2]和文献[3]方法;本文方法所得误差波动较小,且最大误差为20 μm,为4种方法中最小,满足机床加工的精度要求。因此,利用本文方法开展五轴联动数控刀具切削加工误差插补后,可提高加工精度并获得较好的插补效果。

3 结束语

为了提高五轴联动数控机床的刀具加工精度,本文提出了五轴联动数控刀具切削加工误差非线性插补方法。根据五轴联动数控刀具工作原理,分析误差产生原因,利用误差非线性插补方法,实现误差插补。实验结果表明:利用该方法进行误差插补后,机床刀具运行轨迹与理想插补轨迹贴合度高,且插补后误差明显减小,可为五轴联动数控刀具的进一步设计优化提供理论支撑。