基于中微尺度嵌套技术的风资源利用率评估方法

刘子瑞,马俊鹏,路晓丽,肖成刚,胡江涛,郭海斌

(宁夏回族自治区电力设计院有限公司,宁夏 银川 750016)

随着城市经济快速发展,传统的化石能源已经难以满足城市供电需求,需要不断寻找可代替传统化石能源的可再生能源。目前我国风能发展前景最为广阔[1-2],然而风能属于间歇式能源,具有较强的随机性和波动性,导致电力企业规划的风电项目在实际应用过程中,风资源利用率评估准确率低,直接造成发电性能稳定性差、发电指标偏离、风资源利用率低等问题[3-4]。

基于此，国内外相关学者十分重视风资源利用率评估方法研究，从风资源分布、气候和地理位置、风速等方面，研究风资源的不确定性和变化规律，提出了粒子群优化算法、改进粒子群算法、高斯回归法、四象限分析法、曲面拟合法等风资源利用率评估方法[5]。文献[6]将山西主要粮食作物气候资源作为研究对象，依据山西主要粮食作物发育资料，选择适宜指数、效能指数、利用指数作为资源利用率评估指标,评估气候资源利用率。文献[7]将光热资源作为研究对象,通过分析光温、光能、热量等资源利用率,评估光热资源利用率。文献[8]根据风资源实际功率特性和分布特征,预测风资源利用率,通过计算风资源利用率误差,考虑风力的不确定性,评估风资源利用率。上述学者研究的风资源利用率评估方法,存在风资源利用率评估值与风资源实际利用率拟合度低的问题。为此,本文提出基于中微尺度嵌套技术的风资源利用率评估方法。

1 基于中微尺度嵌套技术的风资源利用率评估方法

1.1 基于中微尺度嵌套技术获取风资源参数

1.1.1建立中微尺度嵌套模型

本文采用中微尺度嵌套技术获取风资源参数,通过中尺度获取风资源利用率评估区域测风塔位置[9-10],以及不同位置测风塔获取的风资源实时数据;微尺度获取风资源参数。根据中微尺度获取的风资源利用率评估数据,设计中微尺度嵌套方案,获取风资源参数。

采用天气研究和预测(weather research and forecasting,WRF)模式获取中尺度3TIER数据源,模拟风电场测风塔位置,生成如图1所示的中尺度模型。

图1 中尺度模型

从图1中可以看出,中尺度模型主要获取区域地形、风资源风速、风向等宏观上的风资源参数,并根据地层起伏、气压、气温等地质、环境参数的变化,模拟风电场测风塔位置。这些参数变化可以通过欧拉坐标进行描述,即:

(1)

式中:K1为环境气压值;K2为测风塔区域顶层气压,即测风塔所在位置的垂直方向上的气压变化情况;K0为近地面气压;γ为大气密度随高度的变化值,即欧拉坐标的变化值。γ∈[0,1],当γ=1时,表示地面数据;当γ=0时,表示大气密度的中尺度数值随着中尺度模型边界风向、风速矢量数据u、v的变化而变化,影响空气密度的数值,进一步影响风速变化值O。

按照上述内容构建的中尺度模型,仅能得到3 km分辨率风资源参数,无法准确模拟20～200 m范围内的地表地貌变化,不能满足风资源利用率评估需求。为此,在WINDSIM及WT软件中采用高分辨率网格,生成分辨率为10 m、水平分辨率为35 m的微尺度模型,获取等流速度、空气密度等数据。

然而,单凭中尺度或微尺度模型都不能获取完整的风资源利用率评估数据。为此,根据中尺度和微尺度模型特征,将中尺度模型作为根,即基础框架,在此基础上嵌套微尺度模型,从而得到如图2所示的中微尺度嵌套模型。

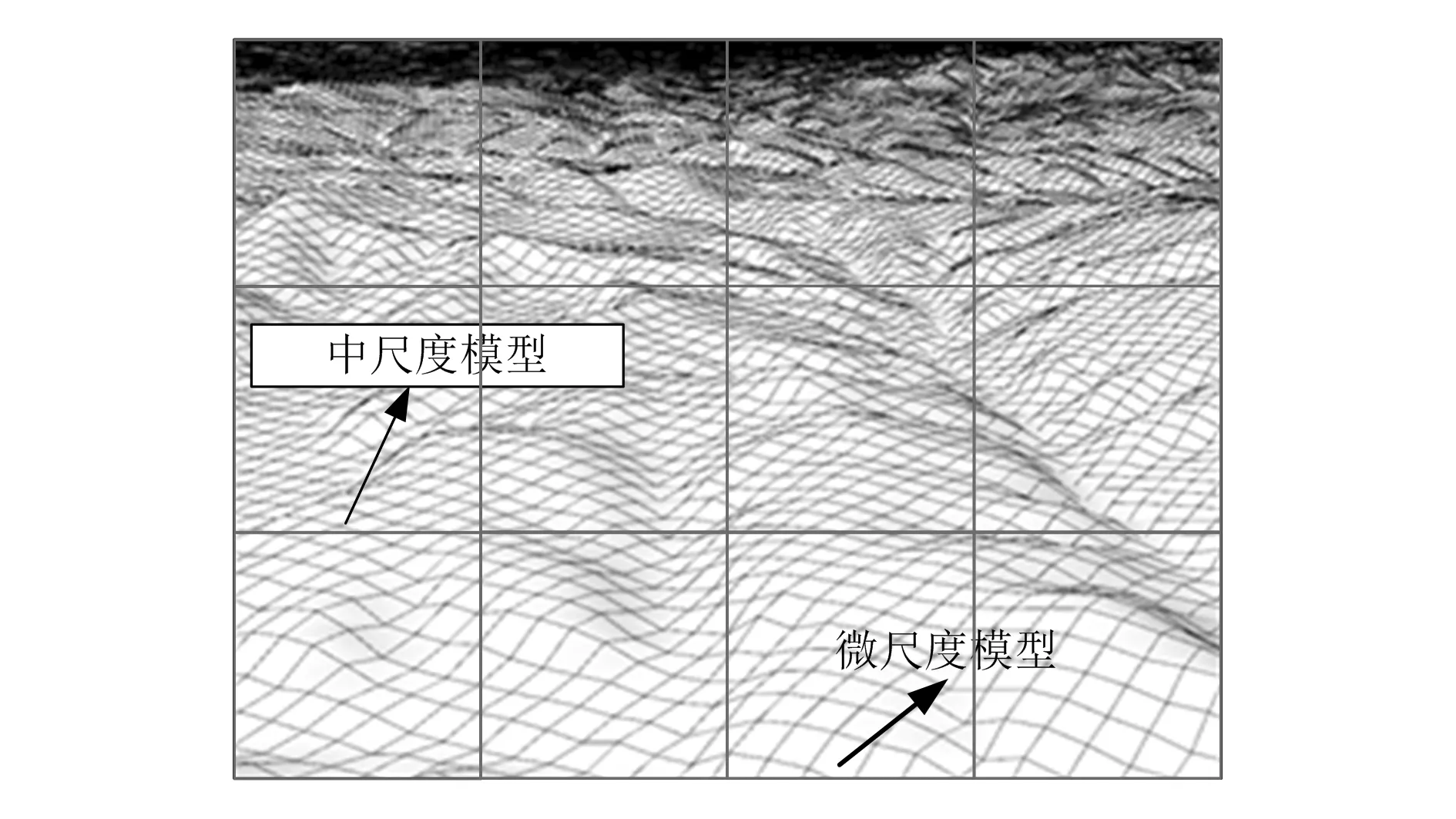
图2 中微尺度嵌套模型

由图2可知,每一个小正方格均为一个微尺度模型,所有大正方格则组成了一个中尺度模型。由中微尺度嵌套模型可得到完整的风资源利用率评估数据。

1.1.2获取风资源利用率评估指标数据

根据中微尺度嵌套模型得到风向数据,按顺时针旋转的度数表示方位,将360°的方位均匀划分为16个方位,风速为v,时间间隔为0.5～1.0 s。

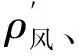
(2)

(3)

(4)

式中:G表示风速等级,v′为中微尺度嵌套模型区域内风力机启动时的风速,v″为中微尺度嵌套模型区域内风力机停机时的风速,t为时间,A为中微尺度嵌套模型划分区域界面,M为中微尺度嵌套模型区域内的测风塔测风次数,v0为测风塔每进行一次测风得到的值,Nt,G为t时间内G等级的风速出现次数,f(v)为风速分布密度函数,f′(v)为风速分布密度函数的理想值,H1、H2为测风塔测量高度,v1、v2分别为H1、H2处的风速值。

1.2 构建风资源利用率评估指标

为了充分反映区域风能资源,分析可以利用的风能潜力,判断不同的风力涡轮机类型和风电场运营方式对风资源利用率的影响,将风资源利用率评估指标划分为开发效率U1、能质效率U2、技术效率U3、接纳效率U4、消纳效率U55个指标,分别对应给定区域的风资源。应用这些指标,对电网调度(平滑)中风电波动和不确定性做出合理响应,以确保电力系统中风电的高效、稳定和可靠消耗。评估指标计算公式如下:

(5)

式中:C1为风电装机容量,C2为实际可开发风能资源总量,C3为全口径累计装机容量,T1为风电场实际年风电利用小时数,T2为风电场实际年风电实际利用小时数,Q1为风电上网电量,Q2为弃风电量,Q3为年发电量,p为年平均弃风率。

1.3 评估风资源利用率

根据式(3)计算得到的风资源利用率评估指标值,构成灰靶理论模式序列δ,即:

δ={δ(1),δ(2),…,δ(i),…,δ(n)}

(6)

式中:δ(i)为第i个状态参数序列,n为风资源状态参数数量。根据式(4)所示的灰靶理论模式序列,假设5个评估指标都具有极大值Umax,且Umax→1,将理想状态下的评估指标均值记为1,得到的理想模式序列δ′(i)为:

δ′(i)={δ′(1),δ′(2),…,δ′(n)}={1,1,…,1}

(7)

依据灰靶理论中的灰靶变换公式,变换灰靶理论模式序列和理想模式序列,则有:

(8)

式中:η表示灰靶变换;δi(n)表示变换后的理想模式序列。经过式(6)变换后,判断δ是否满足式(9)所示的条件:

(9)

若δ满足式(9),则可以将δ0记为灰靶理论的靶心。此时,可根据δ0计算靶心度λ(δ0,δi),评估风资源利用率,则有:

(10)

P=λ(δ0,δi)

(11)

式中:Δ0i(n)为δ0(n)与δi(n)的差值,Δ0i(max)、Δ0i(min)分别为Δ0i(n)的最大值、最小值,P为风资源利用率评估值。

通过计算风资源利用率评估指标值,即可逐一匹配该指标值,从而实现对风资源利用率的评估。

2 实例与结果分析

将某区域的风电场作为研究对象,选择复杂地形风场的评估方法和面向风电机组功率模型的评估方法作为对比方法,以对比实验的方式验证基于中微尺度嵌套技术的风资源利用率评估方法(本文方法)。

2.1 风电场背景介绍

在某区域的平坦草原上,历时 1年零1个月,建立了12 km2、49.5 MW容量的风电场,该风电场共安装了35台金风GW82-1.5MW风机。据该风电场规划,其每年采用风资源的发电量预计为1.24 GW·h。

从风电场中,选取1号和2号测风塔近一年(366天)测得的数据,将测风塔高度为20 m、45 m、60 m、70 m的相关数据作为评估样本。1号和2号测风塔每间隔10 min采集一次风资源数据,共采集了52 704个风资源数据。

2.2 实验结果

2.2.1风资源指标数据获取

根据测风塔采集到的不同轮毂高度数据,使用3种评估方法,分别获取风资源平均风速a(m/s)、平均风能密度b(W/m2)、有效风能密度c(W/m2)、功率d(W)4项指标数据,得到的风资源指标数据见表1。

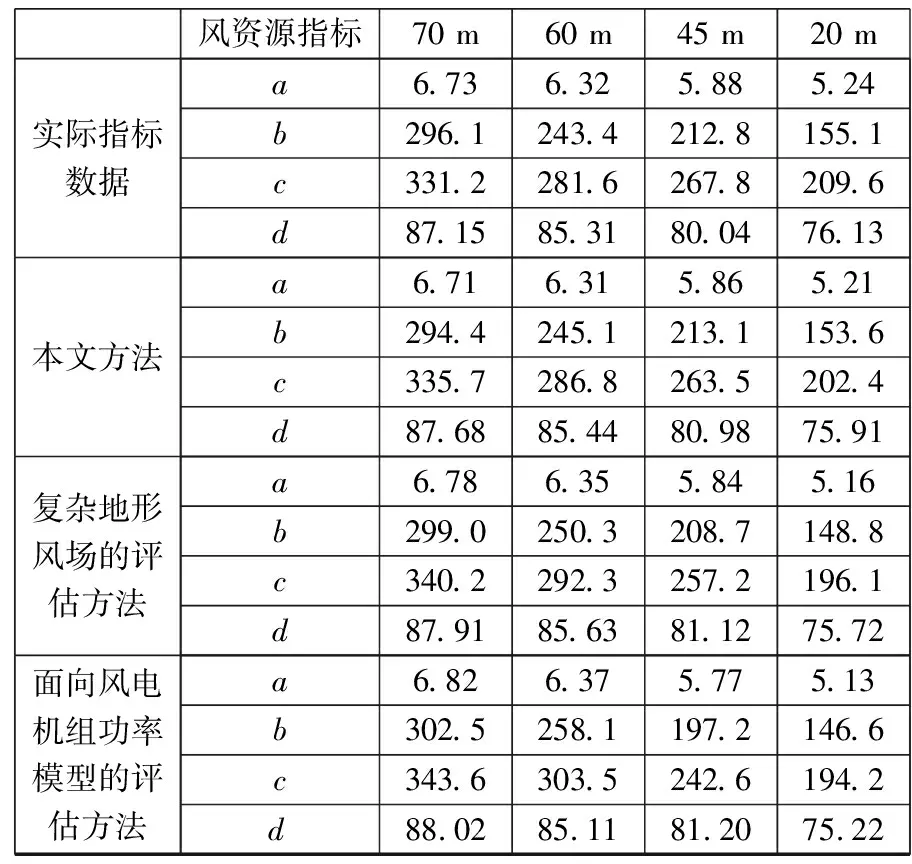
表1 风资源指标数据

2.2.2风资源利用率评估结果拟合度

根据3种方法获取的风资源指标数据,分别评估风电场对不同轮毂高度风资源利用率,并将3种方法评估风资源利用率结果与实际利用率进行拟合,得到如图3所示的风资源利用率评估拟合效果图。

从图3可以看出,复杂地形风场评估方法得到的风资源利用率较实际值偏低,面向风电机组功率模型的评估方法得到的风资源利用率较实际值偏高,而本文方法评估的风资源利用率与实际值完全吻合,具有很高的拟合度。由此说明,利用本文方法对风电场的风资源利用率进行评估时,其评估结果与实际值非常接近,表明本文方法在风资源利用率评估方面具有较高的准确性和可靠性。

3 结束语

本文充分利用中微尺度嵌套技术,通过采集完整的风资源指标数据,并计算得到准确的风资源利用率评估指标值。通过对比风资源实际利用率,确认了评估值与实际利用率之间的拟合度,可为获取风电工程投资收益率及申报电价,提供更为准确的数据依据。