突风响应在时域及频域中的分析方法研究

刘滢滢

(1.哈尔滨工业大学航天学院,黑龙江 哈尔滨 150001)(2.中国商用飞机有限责任公司上海飞机设计研究院,上海 201210)

不同于军用飞机,民用飞机较少进行机动动作,因此突风和紊流载荷成为民用航空规章[1]中明确规定要考虑的设计载荷。按CCAR-25-R4$25.341(a)(1)规定,必须通过动态分析,给出结构各部分的限制突风载荷。随着现代民用飞机向大型化发展,飞机的结构弹性增加,突风动态响应载荷已成为民用飞机最重要的设计载荷情况之一,自初步设计阶段至取证阶段都需要给出突风载荷在全机的分布情况,用于评估飞机结构强度情况。突风载荷已成为机翼、平尾等部件的设计载荷,也是全机静力试验的重要输入,其量值对机翼及平尾结构强度设计至关重要,突风载荷增大不利于结构减重,同时突风振动响应会影响飞机上乘员的舒适性和飞机结构疲劳寿命。

民用飞机设计使用的突风激励已在适航规章(CCAR-25-R4$25.341)中明确规定,突风激励包括离散及连续两种激励形式。离散突风速度与突风梯度、飞行高度、飞行速度、飞机载重情况等有关,其相位及幅值明确。连续突风速度与飞行高度、飞行速度、飞机载重情况等有关,其输入为突风速度的功率谱密度形式,无明确的相位及幅值信息。

在激励明确的情况下,突风分析方法以及突风分析模型的修正方法发展比较充分[2-3]。针对电传飞机的控制律,早期飞机设计过程中,通常开展不考虑电传控制律的开环突风载荷计算及强度校核过程,后期飞机设计过程则是利用主动控制技术[4-5]来减缓闭环突风载荷。

根据是否考虑控制律,可将突风分析分为开环突风载荷分析及闭环突风载荷分析两种,闭环突风载荷分析使用的控制律应根据飞机运行场景进行选择,通常包括增稳控制律、自动飞行控制律、突风载荷减缓控制律等。

在气弹分析过程中,突风载荷分析可在时域及频域开展。工程中每一轮次的突风计算工况数以万计,通常采用频域分析,计算速度快,优势明显,缺点是在频域中开展闭环分析时,需对控制律进行线性化处理,难以考虑闭环分析时的非线性限制,如舵偏角度、舵面偏转速率限制等。时域突风载荷分析可避免上述问题,这是因为气动力影响系数矩阵与频率相关,实施过程需对气动力影响系数矩阵进行有理化拟合[6],通常在Simulink中开展状态空间的时域突风载荷计算[7]。由于连续突风缺乏相位及幅值信息,因此可使用等效方法转换为离散突风激励[8]。针对舵偏限制等非线性约束时,可直接在Simulink中开展状态空间的时域非线性闭环突风载荷计算,亦可使用卷积方法,将该非线性约束通过时域处理加入到频域计算过程中[9]。

在工程中,有多种方法可用于突风载荷分析过程,但缺乏优缺点的对比。为此本文构建大展弦比单机翼突风计算模型,针对开环及闭环响应,采用5种分析方法,通过对比,分析结果的差异及造成差异的原因。从气动力影响系统矩阵的插值精度及气动力系数矩阵的有理化处理过程精度等方面,给出造成不同突风响应计算结果的原因及改善方法,提高工程中突风载荷分析的效率和精度。

1 突风分析方法

1.1 弹性飞机突风响应频域分析方程

在模态坐标系,不考虑控制面偏转时,建立开环弹性飞机的气动弹性频域分析方程如下:

[-Mhhω2+iChhω+(1+ig)Khh-

(1)

式中:Mhh为广义质量矩阵;ω为圆频率;i为虚数单位;Chh为广义阻尼矩阵;g为结构阻尼;Khh为广义刚度矩阵;ρ为大气密度;V为飞行速度;m为马赫数;k为减缩频率,k=ωb/V,其中b=c/2,即气动力参考弦长c的一半;q为模态幅值向量;{P(ω)}为转换至模态坐标系的外激励;h为模态坐标;Qhh(m,k)为广义气动力系数矩阵。

考虑控制面偏转时,建立闭环分析方程如下:

[-Mhhω2+iChhω+(1+ig)Khh-

k))δ+{P(ω)}]

(2)

式中:Mhc为广义舵面耦合惯性质量矩阵,Qhc(m,k)为广义舵面气动力影响系数矩阵,δ为对应于舵面刚体偏转的广义坐标。

1.2 弹性飞机突风响应时域分析方程

为建立突风时域状态空间分析方程,以开环分析为例。

1)对式(1)中的频域非定常气动力系数Qhh,通过最小状态法进行有理函数拟合,如下:

(3)

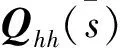
将式(1)变换至拉氏域,以式(3)替换式(1)中的Qhh,经过整理可得:

(4)

(5)

式中:xa为气动力增广状态向量。

2)对时域突风激励进行离散处理。因突风气动力影响系数矩阵已考虑突风参考点与气动面元之间的距离,并已考虑该距离对受激励的当地气动面元攻角变化的时滞影响,采用傅里叶变换及逆变换结合的方法得到突风激励的广义力,不对突风频域激励进行有理化。

对参考点处的任意离散突风速度wg进行傅里叶变换,得到离散突风速度的频域形式f(wg(t)),将突风气动力影响系数Ag(ω)与其相乘,得到突风激励气动力的频域形式fg(ω),如式(6)所示。

(6)

对式(6)进行傅里叶逆变换,得到时域上各模态的广义力,如式(7)所示。

(7)

式中:fg(t)为突风激励气动力的时域形式,f(·)代表傅里叶变换,f-1(·)代表傅里叶逆变换。

完成非定常气动力影响系数矩阵有理化处理以及离散突风激励的傅里叶逆变换后,可建立弹性飞机在状态空间中的开环气动弹性响应方程。

(8)

(9)

其中:

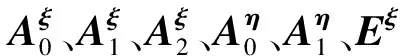
建立弹性飞机在状态空间中的突风载荷开环分析方程和突风载荷闭环分析方程,对Qhc的有理化处理过程与对Qhh的有理化过程一致,与式(8)及式(9)类似,闭环状态空间方程如式(10)及式(11)所示。

(10)

(11)

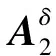
2 弹性飞机突风响应结果对比

建立用于突风计算的民用飞机单机翼模型,对比突风响应结果。

2.1 突风分析模型

图1所示为民用飞机的单机翼结构模型示意图,单机翼长16.24 m,展弦比为9。结构简化为位于部件刚轴坐标系中上的弹性梁,由梁元组成,结构质量及燃油质量离散化为集中质量单元,加载在梁元相应结构节点位置。图2所示为单机翼气动模型,将单机翼的气动面简化为气动面元,采用偶极子格网法计算非定常气动力,气动力通过样条函数插值后产生的插值气动力施加在结构节点处。副翼部位的气动模型仅用于与副翼结构模型耦合计算。单机翼刚体模态部分包括沉浮及俯仰自由度,弹性模态计算至30 Hz,翼梢模态已充分包含在动态响应中。表1给出单机翼模型的前5阶固有频率。图3所示为副翼偏转模态。单机翼的一弯模态频率为2.38 Hz,模态如图4所示。

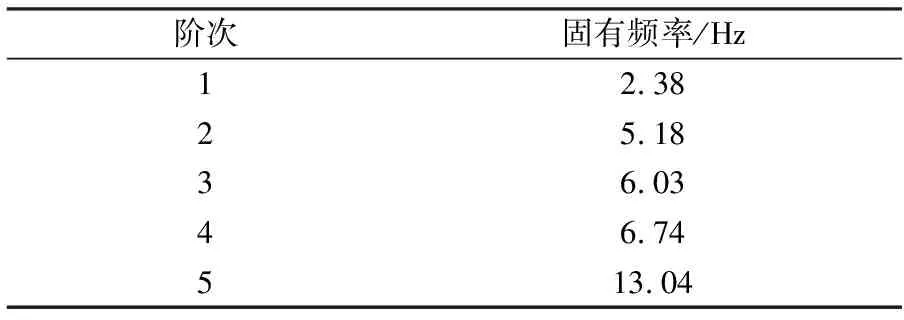
表1 固有频率

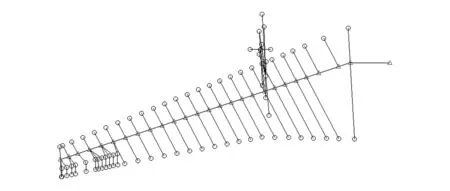
图1 单机翼结构模型示意图

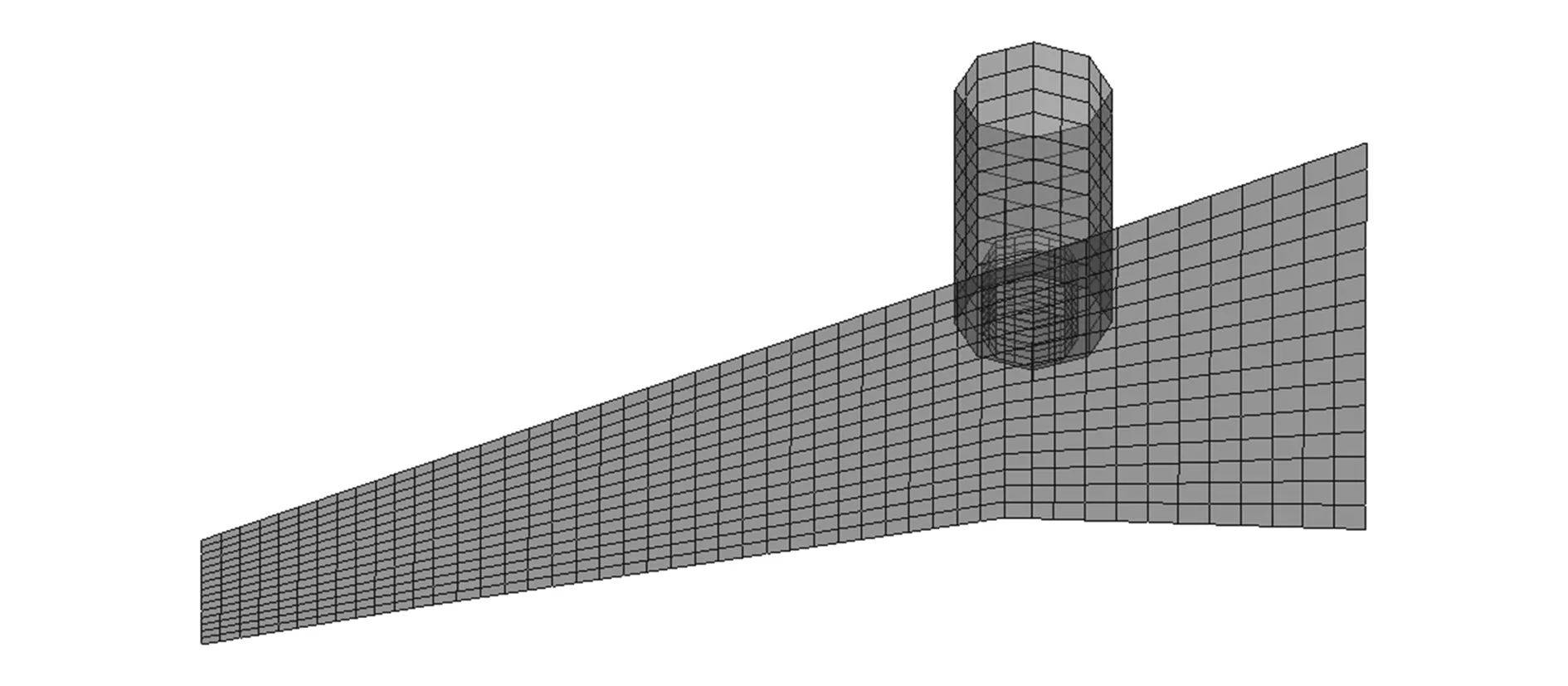
图2 单机翼气动模型示意图

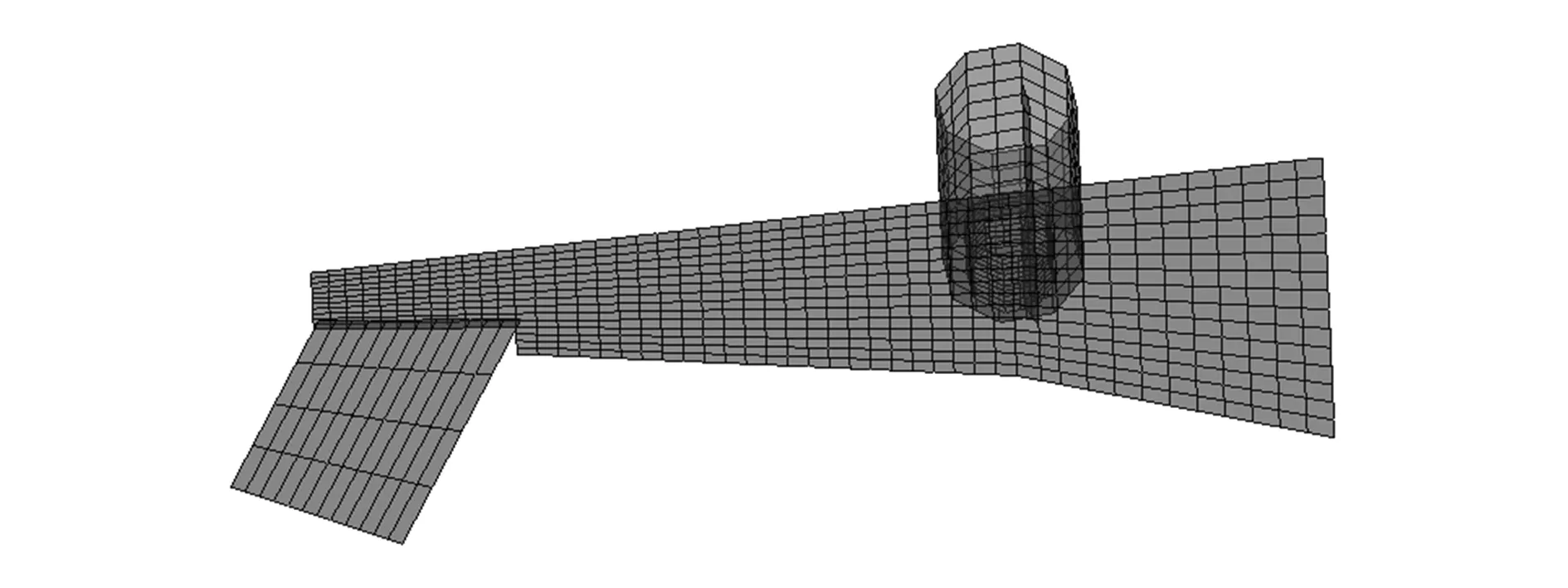
图3 单机翼副翼偏转模态示意图

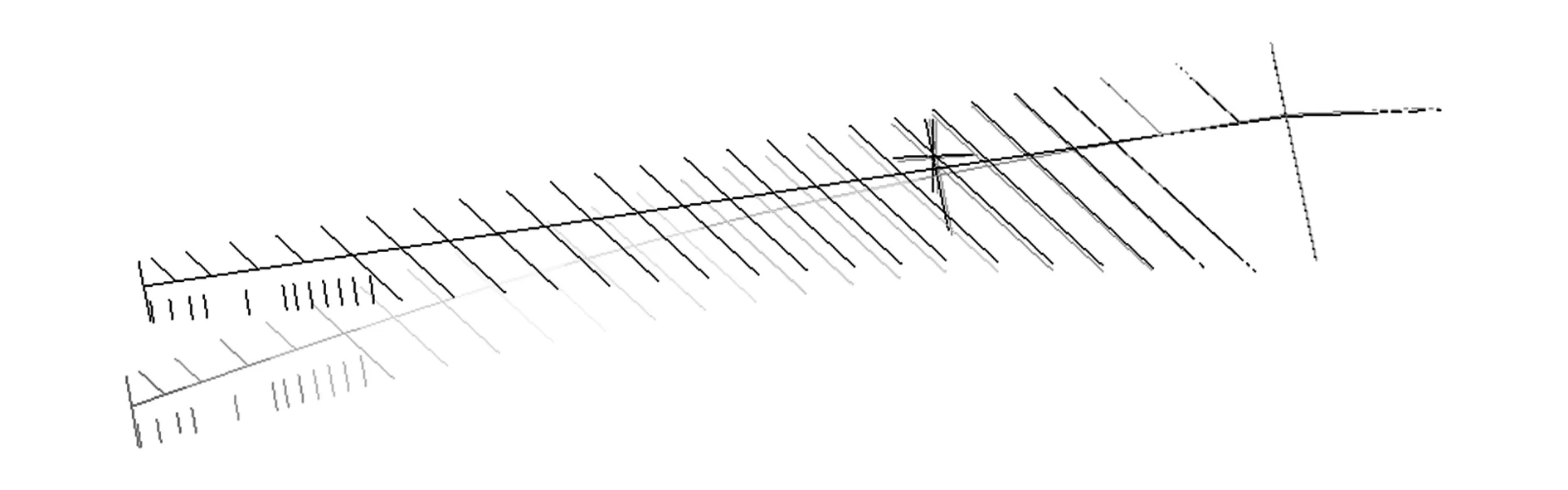
图4 单机翼一弯模态示意图

2.2 突风开环分析结果对比

针对单机翼模型的开环时域响应,输入如图5所示“1-COS”型幅值为1的离散突风激励,突风速度为1 mm/s,激励频率为2.44 Hz,分别采用以下4种分析方法进行分析:基于MSC.Nastran的频域分析;基于Zaero的频域分析;基于Zaero的时域分析(采用最小状态法);对气动力影响系数矩阵有理化处理,对突风激励进行傅里叶逆变换,在Simulink中实现状态空间内的时域响应分析。对比翼梢处的加速度响应,如图6所示。

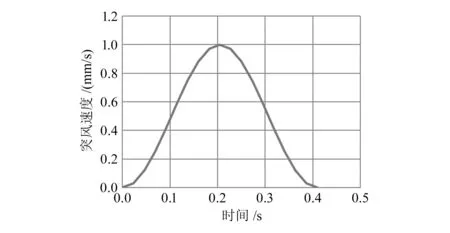
图5 离散突风速度的输入

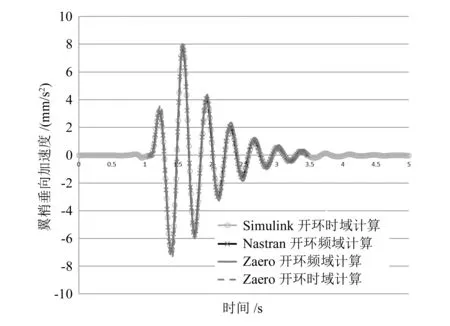
图6 翼梢加速度开环时域分析结果对比

图6显示,使用上述4种方法,翼梢加速度时域响应基本一致,抽取其最大值及最小值,见表2。

由表2可知,以基于MSC.Nastran的开环频域分析结果为参考值,用基于Zaero的频域分析结果,及在Simulink中实现状态空间内的时域响应分析结果与参考值相比,翼梢加速度最大值及最小值与参考值相差的绝对值小于2.5%;而基于Zaero的时域分析,翼梢加速度最小值相差为6.4%,最大值偏差为-0.1%。造成6.4%差异的原因是有理化过程迭代次数不同,生成的状态空间矩阵与Simulink生成的矩阵不同,通过在突风激励频率附近增加迭代次数,同时在基于MSC.Nastran及基于Zaero的突风频域分析过程中,增加用于气动力影响系数矩阵的插值的减缩频率k的数量,可降低上述差异。

针对单机翼模型的开环突风频域分析,输入幅值为1 mm/s的连续突风激励,采用基于MSC.Nastran的频域分析、基于Zaero的频域分析以及通过式(9)编程求解传递函数的方式,以0.1 Hz的间隔,检查翼梢处的开环加速度响应,如图7所示,在2.8 Hz,加速度达到第一个极大值。

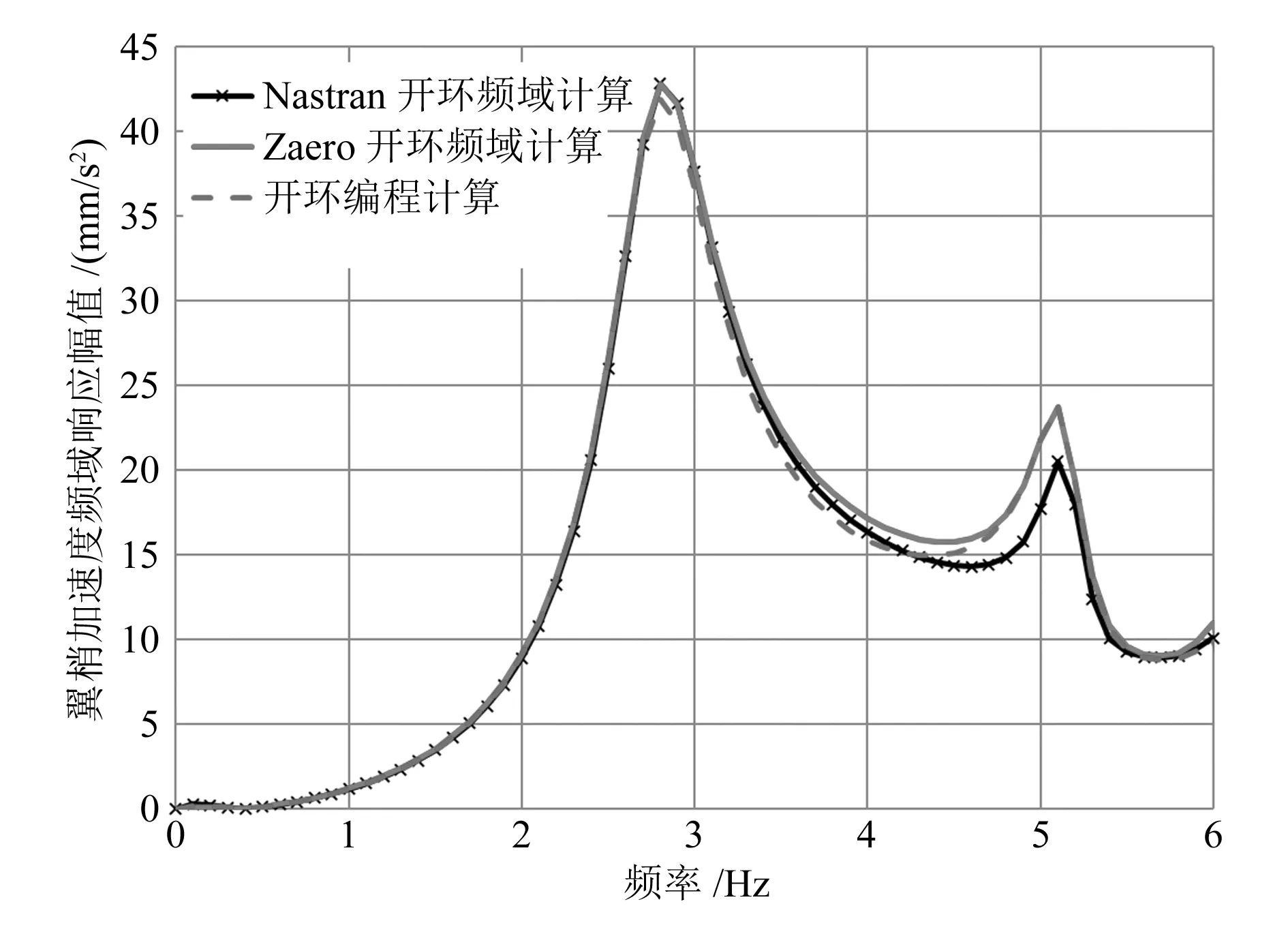
图7 翼梢加速度开环频域分析结果对比

图7显示,使用上述3种方法,翼梢加速度频域响应基本一致。分别抽取2.8 Hz处3种方法的极大值,见表3。

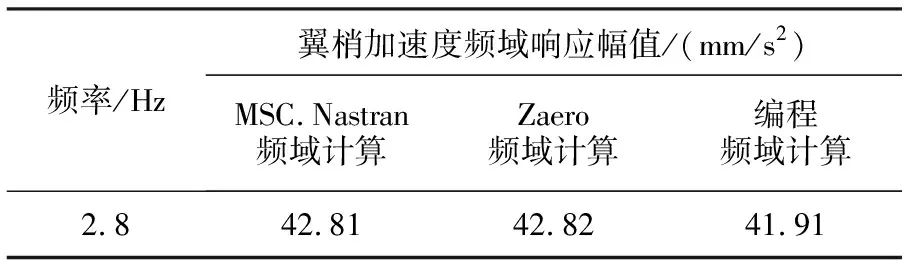
表3 单机翼翼梢开环频域加速度最大值结果对比

由表3可知,以基于MSC.Nastran的开环频域分析结果为参考值,用基于Zaero的频域分析结果及式(9)编程求解传递函数的分析结果,对比翼梢加速度频域响应幅值,差异绝对值小于2.1%,原因在于Qhh使用多个减缩频率k插值给出所求频率点的Qhh的拟合值,编程计算时的插值方式为直接内插的方法,与MSC.Nastran及Zaero使用的special插值方式不同,通过不断增加用于气动力影响系数矩阵的插值的减缩频率k的数量,可降低上述差异。

2.3 突风闭环分析结果对比

针对单机翼模型的闭环时域响应,输入如图5所示的离散突风激励,并添加控制律,以翼梢垂向加速度(单位为mm/s2)作为输入量,输出量为副翼偏转角度(单位为rad),增益为2.5E-06,使用相同作动器传递函数,分别采用以下4种方法对比翼梢处的时域加速度响应:基于MSC.Nastran的频域分析,基于Zaero的频域分析,基于Zaero的时域分析(采用最小状态法),在Simulink中采用最小状态法实现状态空间内的时域响应分析(图8给出其连接图),如图9所示。

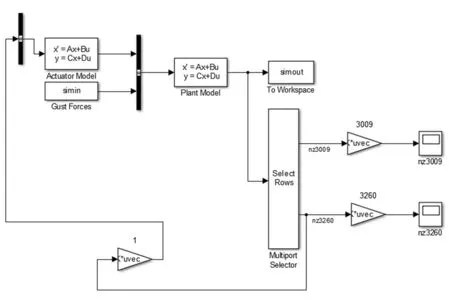
图8 Simulink闭环分析连接示意图

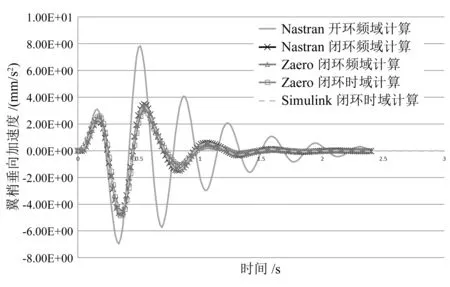
图9 翼梢加速度闭环时域分析结果对比

图9显示,上述4种方法的翼梢加速度时域响应基本一致,加入控制律后,副翼偏转后,使气动力破升,翼梢加速度明显降低,抽取其最小值,见表4。

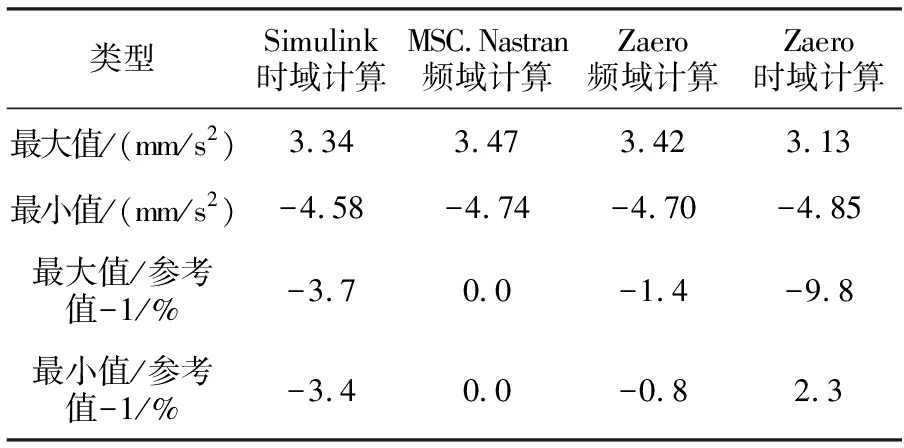
表4 单机翼翼梢闭环时域加速度最值对比

由表4可知,以基于MSC.Nastran的闭环频域分析结果为参考值,对比基于Zaero的频域分析结果以及基于Simulink的状态空间内的时域响应分析结果,与参考值相比,翼梢加速度最值相差百分比的绝对值小于3.7%;而基于Zaero的实现状态空间的时域分析,翼梢加速度最小值相差百分比的绝对值为2.3%,最大值偏差的绝对值为9.8%。造成9.8%差异的原因是有理化过程迭代次数不同,生成的状态空间矩阵与Simulink生成的矩阵不同,通过在突风激励频率附近增加迭代次数,同时在基于MSC.Nastran及基于Zaero的突风频域分析过程中,增加用于气动力影响系数矩阵的插值的减缩频率k的数量,可降低上述差异。

针对单机翼模型的闭环频域响应,输入幅值为1 mm/s的连续突风激励,分别采用基于MSC.Nastran的频域分析、基于Zaero的频域分析,以0.1 Hz的频率间隔,检查翼梢处的闭环加速度响应,如图10所示。

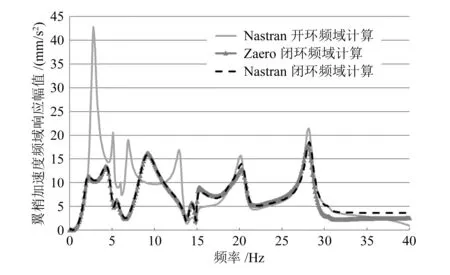
图10 翼梢加速度闭环频域分析结果对比

图10显示,基于MSC.Nastran闭环频域分析及基于Zaero闭环频域分析的结果一致,加入控制律后,副翼偏转后,使气动力破升,翼梢加速度明显降低,垂向加速度均方根值由4.83 mm/s2降至2.67 mm/s2,减小44.66%,起到了降低翼梢加速度的作用。

3 结论

1)针对开环及闭环突风响应,对基于MSC.Nastran的频域分析;基于Zaero的频域分析;基于Zaero的时域分析;有理化处理气动力影响系数矩阵,傅里叶逆变换突风激励,在Simulink中实现状态空间内的时域响应分析;传递函数编程分析等5种分析方法进行比较,可知不同的突风分析方法无本质差别,在时域及频域分析的突风分析结果基本一致。

2)受制于气动力影响系统矩阵的插值精度及气动力系数矩阵的有理化处理过程精度,不同计算方法的突风响应计算结果略有不同,通过增加气动力插值及有理化拟合的精度,可以降低不同突风分析方法的响应结果的差异。