基于递归最小二乘法的协作机器人柔顺性控制问题研究

吕文艳,刘会景

(乌鲁木齐职业大学应用工程学院,新疆 乌鲁木齐 830002)

目前,协作机器人主流控制方法主要包括基于PID的控制方法和线性反馈控制方法以及阻抗控制方法。如宋昌宝等[1]基于PID控制理论,提出一种基于模糊自适应PID控制机器人的方法,可实现机器人精确的点到点及任意转角的运动控制,具有较高的准确性。徐鑫等[2]结合状态估计和反馈控制设计具有状态估计的反馈控制器,同时引入线性二次调节器,提出一种基于线性二次调节器算法的两轮自平衡机器人最优控制方法,具有良好的稳定性和鲁棒性,实现了平衡机器人运动平衡控制。余晓兰等[3]提出一种控制双臂人形机器人阻抗一致性的方法,实现了双臂人形机器人的阻抗一致性控制,可向协作机器人提供良好的动态性能。通过上述研究可以发现,在对协作机器人实施控制时,无论是机器人的运动轨迹控制还是柔顺性控制,均取得了一定成果,但杨桂林等[4]在协作机器人柔顺运动控制综述中认为,协作机器人的柔顺性控制应该随刚度环境变化而变化,但传统基于阻抗控制的控制方法不能表现这种变化,导致控制效果有待进一步提高。为解决该问题,本文提出一种基于递归最小二乘法的协作机器人柔顺性控制方法。

1 协作机器人动力学模型

协作机器人的动力学模型通常包括完整动力学模型和简化动力学模型两类。其中,简化动力学模型就是在完整动力学模型的基础上忽略机器人电机和连杆的耦合关系,认为机器人电机转子的动能由转子相对上一连杆的相对运动决定。根据协作机器人关节柔性主要来自内嵌扭矩传感器和谐波齿轮形变,与电机和连杆的耦合关系较弱的特点,采用简化的动力学模型作为协作机器人的动力学模型。

简化的动力学模型可表示为:

(1)

2 基于递归最小二乘法的协作机器人柔顺性控制

2.1 动力学参数求解

动力学参数求解是实现协作机器人控制的前提,只有预先获取协作机器人的质心位置、连杆质量等动力学参数,才能实现机器人的运动控制。结合上述简化的协作机器人动力学模型以及协作机器人实际控制需求,采用递归最小二乘法[5]对协作机器人动力学参数进行求解。

根据文献[6]可知,协作机器人的动能和势能与其连杆惯性参数线性相关。因此,当外力条件为零时,可采用拉格朗日法计算机器人的动力学,得到机器人连杆动力学模型为:

(2)

(3)

式中:q为连杆角度,Y为系统状态变量集合,p为最小惯性参数集。由式(2)～(3)可知,参数识别就是求式(2)的线性方程,而要获取p,则需要获取10个以上不同位置测量的机器人角位置、角速度、关节传递力矩和角加速度,然后采用递归最小二乘法对简化的动力学模型参数进行辨识[7],具体如式(4)所示:

(4)

K(N+1)=P(N)φ(N+1)[1+φT(N+1)P(N)φ(N+1)]

(5)

P(N+1)=P(N)-K(N+1)φT(N+1)P(N)

(6)

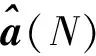
采用递归最小二乘法求解式(4)～(6),可得到协作机器人电机转子端和连杆端的简化动力学参数。

整体基于递归最小二乘法的协作机器人动力学参数识别流程可概括为图1[8]。

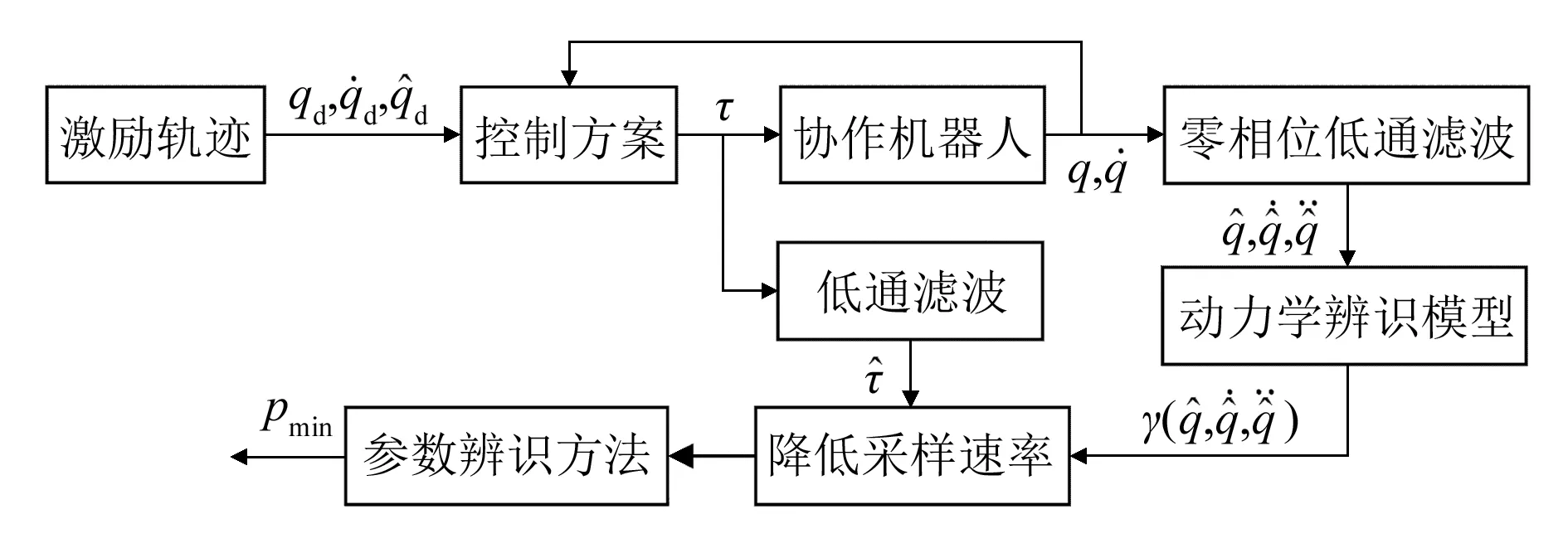
图1 基于递归最小二乘法的机器人参数识别

2.2 协作机器人的柔顺控制

协作机器人的柔顺控制,即在协作机器人与环境发生接触时,保证协作机器人与环境刚接触的柔顺性,避免机器人与环境发生碰撞。目前,协作机器人的柔顺控制,主要包括阻抗控制和导纳控制两种方法。其中,阻抗控制可在高刚度环境接触中向机器人提供良好的动态性能,具有较强的鲁棒性,但在较低刚度环境接触中,容易导致机器人系统位置跟踪误差较大;而导纳控制与之相反,在高刚度环境下接触中存在控制不稳定性,在低刚度环境接触中具有良好的控制性能。因此,笔者为实现协作机器人可在各种刚度环境中实现柔顺控制,结合阻抗控制与导纳控制,提出一种基于阻抗/导纳的混合控制方法。阻抗/导纳混合控制系统中,基于阻抗/导纳加权方式的控制器是一种直接的混合控制方法,其基本原理为对阻抗控制和导纳控制进行加权平均计算,得到混合控制系统的控制律[9]:

τH=(1-w)τ1+wτA

(7)

式中:τH为混合控制器输出力矩,w为权重,τ1为阻抗控制器输出力矩,τA为导纳控制器输出力矩。

3 仿真实验

3.1 实验环境搭建

在Simulink软件上搭建本文设计的基于递归最小二乘法的协作机器人柔顺性控制器的仿真模型,如图2所示。

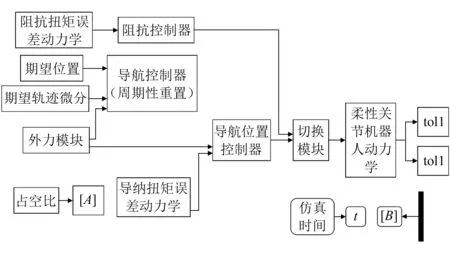
图2 控制器仿真模型图

3.2 仿真模型构建

引入摩擦力,得到协作机器人动力学模型如式(8)[10]所示:

(8)

式中:τf为机器人摩擦外力矩。

此外,考虑到协作机器人关节之间存在阻抗响应,将环境模型转换为多维度形式,得环境刚度Ke。同时,环境接触外力Fext为:

Fext=-Ke(X-Xe)

(9)

τext=JTFext

(10)

JT=

(11)

式中:X为机器人末端位置,Xe为环境初始位置,JT为力雅可比转置矩阵,l1、l2分别为大臂和小臂连杆长度,q1、q2分别为大臂和小臂连杆转角。

3.3 参数设置

设仿真步长为1 ms,关节刚度为diag(12 000 N·m/rad,12 000 N·m/rad),仿真周期为0.02 s,期望惯性为diag(1 N·s2/m,1 N·s2/m),关节阻尼为diag(0.013 N·ms2/rad,0.013 N·ms2/rad),比例增益为diag(10 000 N/m,10 000 N/m),小臂长度为0.365 m,特征速度为0.56 rad/s,微分増益为diag(50 N·s/m,50 N·s/m),微观阻尼为600 N·m/rad,重力系数为9.8 m/s2,大臂长度为0.375 m。

3.4 评价指标

为定量分析本文设计的基于递归最小二乘法的协作机器人柔顺性控制器的阻抗动态性能,选用质量-弹簧-阻尼系统的理想关节位移对其进行评估。

3.5 结果与分析

3.5.1混合控制系统加权比确定

由于基于加权方式的阻抗/导纳混合控制系统中,不同加权比具有不同的控制效果,因此为确定最佳加权比,在不同环境刚度下设置不同加权比,通过观察关节误差曲线进行确定。

将基于加权方式的阻抗/导纳混合控制系统置于1、500、3 000、10 000 N/m对应的极软、软、中、硬4种环境刚度下,并设置协作机器人初始位置(0.74 m,0 m),末端虚拟平衡点Xd和环境位置Xe均为(0.50 m,0 m)。当机器人与环境发生碰撞后,Xd位置变化为(0.60 m,0 m)。

图3所示为不同加权比下协作机器人关节误差曲线。由图可知,不同环境刚度条件下,协作机器人关节误差曲线变化趋势存在一定差异,在极软刚度环境中,关节误差曲线发生了阶跃性变化,在硬刚度环境条件下,关节误差曲线在0.1 s时发生了突变,但无论是在何种环境刚度下,当加权比n1为0.8时,混合控制系统的物抗误差均最低,混合控制系统表现出最优性能。因此,本次实验设置基于加权方式的阻抗/导纳混合控制系统的加权比为0.8。

3.5.2混合控制系统性能验证

为验证所提控制方法的动态性能,设定10 N/m(极软)、500 N/m(软)、3 000 N/m(中)、10 000 N/m(硬)4种环境刚度,并以阻抗/导纳混合控制系统为载体进行仿真,从而得到不同环境刚度下控制器的控制误差。

图4所示为阻抗控制在不同环境刚度下的协作机器人关节空间误差曲线。由图可知,在极软和软的环境刚度下,所设计的控制器前期误差振荡幅度较大,但可快速达到稳定状态;在硬环境刚度下,控制器的响应误差先快速振荡,后稳定于0。由此说明,本文所设计的控制器可在硬环境下具备良好的动态响应性能。

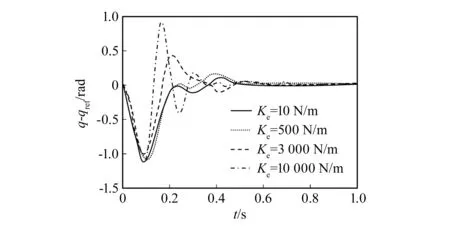
图4 阻抗控制关节空间误差曲线

图5所示为导纳控制在不同环境刚度下协作机器人的关节误差曲线。由图可知,当机器人末端在极软环境和软环境下发生接触时,控制器的导纳控制关节空间误差快速达到稳定并趋于0;当机器人末端在刚度适中的环境发生碰撞时,控制器的导纳控制关节空间误差前期出现较大幅度的振荡,后期趋于稳定,但其达到稳定所消耗的时间明显高于极软环境和软环境;当机器人末端与硬刚度的环境发生碰撞时,控制器的导纳控制关节空间误差出现较大误差且不能达到稳定状态。整体来看,本文所设计的控制器在存在外力条件下,具有一定的稳定性。

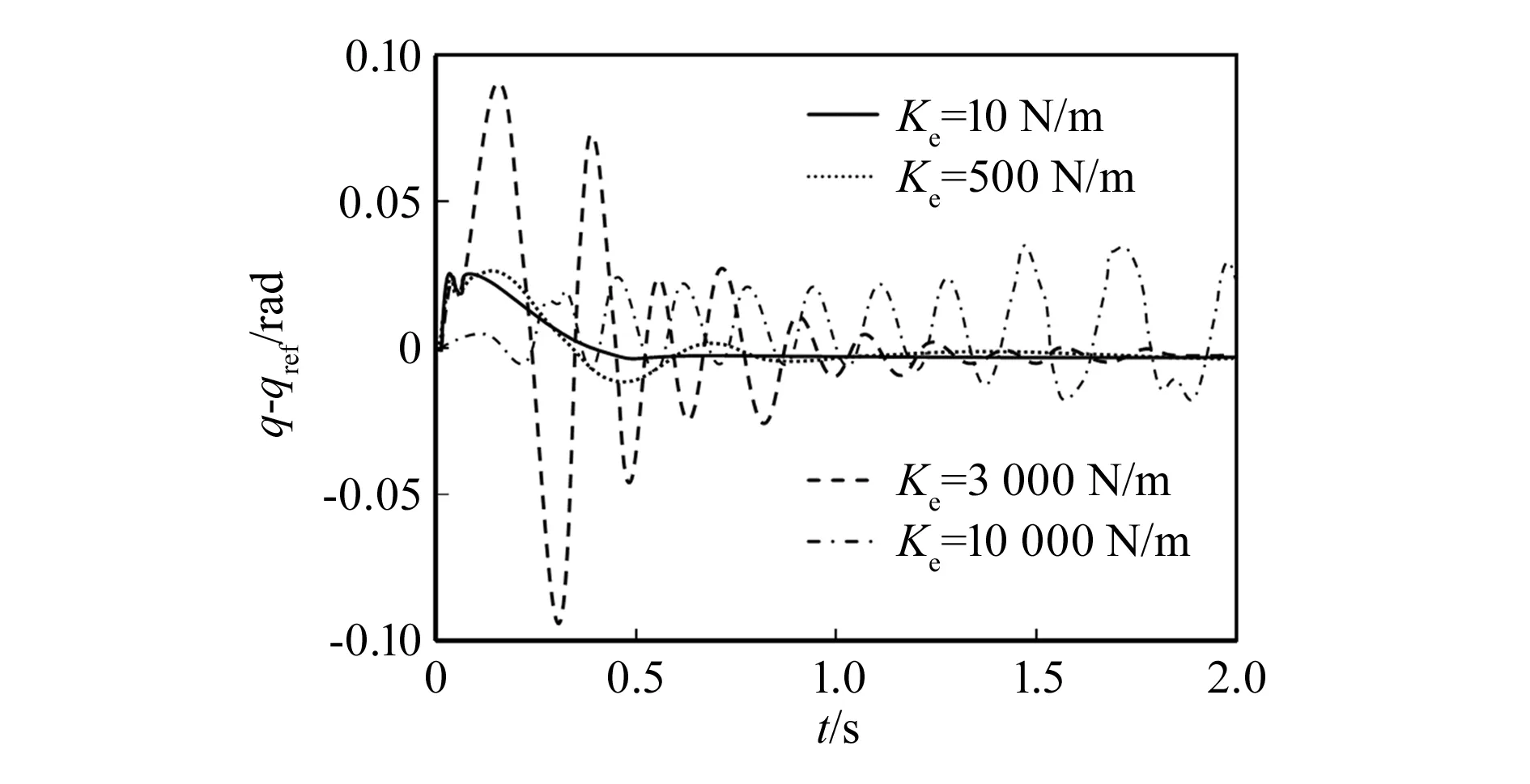
图5 导纳控制关节空间误差曲线

图6所示为不同环境刚度下基于加权方式的阻抗/导纳混合控制系统的协作机器人关节空间误差曲线。由图可知,当环境刚度较软时,混合控制系统更接近导纳控制系统,具有良好的控制效果,关节空间误差较小;当环境刚度较硬时,混合控制系统更接近阻抗控制系统,系统可快速达到稳态,具有较强的阻抗响应和鲁棒性。

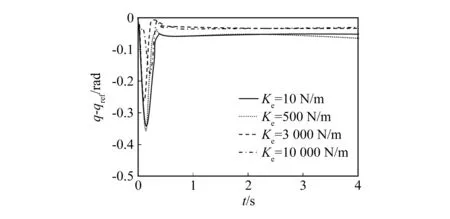
图6 阻抗/导纳混合控制系统的关节空间误差曲线

对比图4、图5、图6可知,基于加权方式的阻抗/导纳混合控制系统可根据不同环境刚度,自动调节控制方法是趋于阻抗还是趋于导纳,具有更理想的控制效果。

3.5.3实际应用效果

为验证基于加权方式的阻抗/导纳混合控制系统的实际应用效果,设计了图7所示时变环境刚度,并将本文所设计的基于加权方式的阻抗/导纳混合控制系统在该环境刚度下对协作机器人进行控制,结果如图8所示。由图8可知,本文所设计的基于加权方式的阻抗/导纳混合控制系统可应对环境刚度变化,实现良好的控制,振荡误差最大为1.5 rad,满足协作机器人柔顺控制在实际应用中的误差需求。此外,由图8可知,当加权比为0.8时,混合控制系统的控制效果最好,与上述结果一致,进一步验证了加权比为0.8时基于加权方式的阻抗/导纳混合控制系统控制效果的优越性。

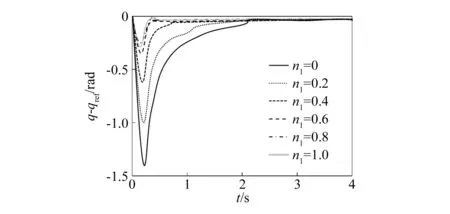
图8 混合控制系统在时变环境刚度下的误差响应曲线

4 结束语

综上所述,本文所提的基于递归最小二乘法的协作机器人柔顺控制方法,通过构建协作机器人简化模型,并采用递归最小二乘法求解协作机器人动力学参数,利用加权方式混合阻抗控制和导纳控制,可实现不同环境刚度下的协作机器人柔顺控制。当环境刚度较小时,本文所提的柔顺控制方法具有较小的响应误差,当环境刚度较大时,本文所提的柔顺控制方法可快速达到稳态,具有较强的阻抗效应和鲁棒性,可用于实际协作机器人的柔顺控制,最大振荡误差为1.5 rad,满足协作机器人柔顺控制实际应用误差需求。