基于EEMDFK和注意力CNN网络的刀具磨损状态识别

吴继春,阳广兴,许 可,周灭旨,胡 柱,范大鹏

(1.湘潭大学 机械工程学院,湖南 湘潭 411105;2.国防科技大学 智能科学学院,湖南 长沙 410073)

0 引言

作为加工制造业的重要组成部分,高速铣削加工领域的优势在于极高的加工效率与加工质量,在进行高速切削加工时,切削刀具的状态对生产效率和表面加工质量有重要影响[1]。机器加工故障是给机械加工制造业造成经济损失的主要原因,其中刀具磨损影响整体的加工效果[2]。

目前,由于切削过程的多样性、复杂性和随机性,现有的刀具检测系统不具有通用性,对刀具状态进行自动监控是迫切需要研究和探索的科研课题。现有刀具磨损检测系统的检测方法分为直接法和间接法。直接法通过直接测量刀具的体积和质量等物理属性的变化来判断刀具的磨损情况,其中有些测量和分析只能人工进行,而且使用范围受限于实际加工条件;间接测量法敏感性较低,会因材料的性质而受到影响。因此开展对刀具磨损状态的识别研究具有重要意义。

刀具状态识别中,通常需要对采集的信号进行预处理,常用的信号处理方法有小波变换(Wavelet Transform,WT)[3]、经验模态分解(Empirical Mode Decomposition,EMD)[4]和傅里叶变换[5]等。李恒等[6]采用傅里叶变换将一维信号转换为二维信号,并将获得的信号输入分类器得到诊断结果;薛小庆等[7]利用小波分析法对振动信号进行处理并进行故障分类;RIZAL等[8]提出一种采用多传感器信号和模式识别系统决策方法对铣削过程中的刀具磨损进行分类和检测的新方法;WU[9]引入一种基于随机森林(Random Forests,RFs)的刀具磨损量预测方法;张吉存等[10]提出将工作过程中刀具的振动信号通过小波包变换转变为能量频谱图,并搭建卷积神经网络自适应提取能量频谱图特征,从而对刀具磨损状态进行分类;孙伟等[11]用EMD对信号进行分解重构,然后采用支持向量机对工件进行故障诊断。传统信号处理方法虽然能够有效地从时域频域中提取故障信息特征进行诊断,但是对信号频率的处理有较高要求,缺乏自适应性;EMD虽然具有独立的自适应性,但是在使用EMD的过程中可能出现极为严重的端点效应和模式混叠现象[12],需要有更好的方法对原始信号进行预处理。

集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)能够解决EMD存在的混叠现象,但是处理信号过程中会将原始信号分解为多种内在模函数(Intrinsic Mode Function,IMF),其中部分IMF存在真实信息量少、信息特征虚假等情况,因此选择具有故障信息特征的IMF非常重要。常用的剔除虚假IMF的方法有相关系数法、灰度关联法、能量比值法、K-S(Kolmogorov-Smirnov)检验法等[13],K-S检验法与灰度关联法在复杂信号区中区分IMF分量的精度不佳,相关系数和能量比值法对信号幅值依赖较大,也不利于区分虚假IMF。因此选择合适的IMF分量是得到信号真实信息的关键。

深度学习模型是一个“端到端的模型”,常在有监督或无监督的特征学习、表示、分类和模式识别中表现良好[14]。随着深度学习的发展,深度学习方法开始逐渐应用于状态监测领域[15]。雷亚国等[16]提出基于深度学习模型对机械装备大数据进行状态监测的方法;曹大理等[17]采用深度卷积网络对刀具能量进行特征提取,并对刀具故障状态进行分类;ZHANG等[18]采用迁移学习和长短期记忆网络预测刀具寿命,并通过实验表明该方法的有效性。综上所述,深度学习能够在状态监测方面取得一定成效,但是如何高效提取特征并避免梯度弥散和过拟合,是一个亟待研究的问题。

综上所述,本文提出一种将经验模态分量选取与注意力机制卷积网络结合的识别方法,以集信号预处理、特征提取与故障分类于一体进行高效智能诊断。针对IMF选取困难的问题,本文引入快速谱峭度图的思想将选取分量转换为选取图片,以提高分量选取效率,降低选取困难,并构建快速谱峭度集合经验模态分解(Ensemble Empirical Mode Decomposition Fast Kurtogram,EEMDFK)算法;同时,引入注意力思想,构建自适应卷积神经网络(Attention Convolutional Neural Networks,ACNN)算法模型,以提高时频图特征的提取效率,并对数据集进行状态识别,实现智能故障诊断。最后通过PHM2010数据集进行实验,验证了该方法的有效性与高效性。

1 信号预处理

1.1 EEMD算法

传统信号分解中,EMD运用广泛,虽然对处理非线性、不平稳的信号具有良好表现,但是在信号分解过程中存在模态混淆现象。WU等[19]提出平均经验模态分解法,对原始信号添加不同白噪声后的信号进行分解,并对分解结果进行平均处理得到最终模态分量。具体步骤如下:

(1)对原始信号z(t)添加一组白噪声信号w(t),得到信号Z(t),

Z(t)=z(t)+w(t)。

(1)

(2)对信号Z(t)进行EMD分解,得到各阶IMF模态分量和剩余分量:

(2)

(3)重复执行(1)和(2),对信号Zj(t)添加白噪声wj(t)得到Zj(t),对Zj(t)进行EMD分解得到对应的IMF模态分量:

(3)

(4)利用白噪声均值为零的性质,将所求的IMF分量求均值得到最终的IMF模态分量mj(t),

(4)

(5)根据文献[19]提出的公式,求噪声幅值wn,

(5)

式中:N为总体平均次数;ε为重构信号与原始信号误差。

1.2 快速谱峭度算法

在实际使用EEMD的过程中,常存在生成的IMF不可控、IMF多数为白噪声等问题,但存在的故障分量信号往往只有一个,如何选取需要的IMF分量是高效识别磨损状态的关键。

针对选取IMF分量方法存在的问题,本文将快速谱峭度图的思想应用于刀具信号模态分量选取中。峭度指标作为时域分析中的一种无量纲参数指标,对信号的瞬时特征非常敏感[20],其基本思想是计算不同频域内的谱峭度值,以准确掌握瞬态信号在频域中所处的位置,因此通过计算不同频域谱峭度值,挖掘不同频域所包含的真实信息,该方法能有效提取不同时刻的刀具磨损状态信息。快速谱峭度算法步骤如下:

(1)构造频率fc=1/8+σ的低通滤波器B(n),基于B(n)分别构造准解析低通滤波器Bd(n)和准解析高通滤波器Bg(n),Bd(n)与Bg(n)设置的频率范围分别为[0,1/4],[1/4,1/2],即

Bd(n)=B(n)ejπn/4,f∈[0,1/4];

(6)

Bg(n)=B(n)ejπn/3,f∈[1/4,1/2]。

(7)

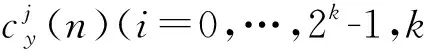
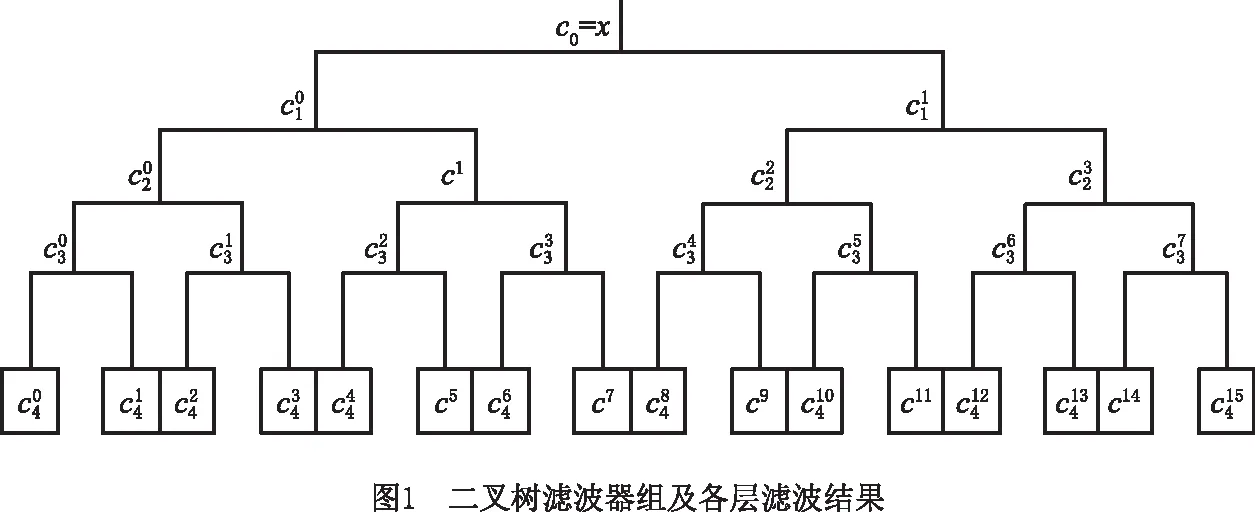
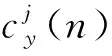
i=0,…,2k-1。

(8)

2 卷积神经网络

在深度学习领域内,卷积神经网络已经成为图像领域的研究热点[21]。传统卷积神经网络结构如图2所示,包括卷积层、激活层、池化层、全连接层。

卷积层中输入图像,每一层卷积层中卷积核与输入特征图进行卷积运算,并将生成的新特征图输入下卷积层。卷积层中,输入特征图与卷积核运算表示为[22]

Xi=Wi⊗Xi-1+B。

(9)

将池化层与卷积层连接,数据通过激活函数在卷积层内输出,激活函数能够提升模型的泛化能力,从而提高学习更加复杂的事物。卷积神经网络中,常用的激活函数有Sigmoid,ReLu,Tanh3种[23]。

池化层可以减少卷积神经网络(Convolutional Neural Networks,CNN)可训练参数的数据维度与数据数量,并能够从激活层的输出特征图中选择具有代表性的特征池化窗口,与卷积层相似,池化窗口可设置不同窗口进行移动运算。常用的池化层方法有平均池化法和最大池化层法两种。

全连接层位于卷积网络分类阶段,该阶段将卷积网络输出的数据特征和分类器连接在一起[24]。CNN通过最后一层卷积层将特征图像转换为一维数组,数组与全连接层相连接,通过分类器输出相应的分类结果。

3 注意力机制

注意力机制类似人脑视觉机制,其通过扫描图像获取特征区域,并划分不同区域的关注度,即对不同特征区域分配不同权重来突出关键信息,从而提高分类效果。图像注意力机制通常分为通道注意力机制(Channel Attention Mechanism,CAM)和空间注意力机制(Spatial Attention Mechanism,SAM)两种。CAM将通道压缩成一维进行权重分配,SAM是以像素为单位进行权重分配。注意力的计算方法为压缩(squeeze)、激活(excitation)、赋值,其中uc为经过卷积运算后的多通道矩阵,通过Fsq平均池化操作将多通道矩阵压缩后以1×1×C的矩阵形式输出,得到zc,

zc=Fsq(uc)。

(10)

通过连接两个全连接层,zc输出与uc同维度的权重矩阵s,

s=Fex(zc,W)=k(W2)·g(W1zc)。

(11)

式中:W演化为两个分别表示与zc运算的全连接层的W1和W2;k和g均表示激活函数,本文采用sigmoid函数作为激活函数。

4 EEMDFK与卷积神经网络刀具磨损状态识别方法

针对刀具磨损难以实时监测且人工经验判断磨损存在误判和漏判的情况,提出基于EEMDFK与注意力机制的CNN磨损状态识别方法,其流程如图3所示,具体步骤如下:

(1)计算总体平均次数和白噪声幅值,将获取的振动信号进行EEMD分解,得到多个分量。

(2)对得到的多个IMF分量进行快速谱峭度计算,得到相关快速谱峭度图中谱峭度所处的最大频带范围。

(3)以原始信号中最大谱峭度值所在的频带为基准,并与各IMF分量中的快速谱峭度图进行对比,若该分量的频带区间属于原始信号的频带范围,则将该分量视为敏感分量,否则视为虚假分量,然后舍弃虚假分量,选择或重构敏感分量。

(4)对选取的IMF分量进行HHT(Hilbert Huang transform)变换,并得到Hilbert-Huang谱。

(5)将得到的Hilbert-Huang谱分为训练集、验证集和测试集。

(6)将训练集批量输入ACNN模型,计算向前传播和向后传播,并保存该模型的权重。

(7)将验证集批量输入ACNN模型,修改学习率、Dropout、迭代次数等超参数,保存最优模型。

(8)将测试集输入最优模型,得到状态判别结果。

5 EEMDFK-ACNN算法的刀具磨损状态识别方法及实例分析

5.1 试验数据

本次实验采用美国纽约预测与健康管理学会(Prognosticsand Health Management,PHM)2010年高速数控机床刀具健康预测竞赛的开放数据,刀具为球头硬质合金铣刀,实验平台如图4所示。主轴运行速度为10 400 r/min,进给速度为155 mm/min。y方向的切割深度(径向)为0.125 mm,z方向的切割深度(轴向)为0.2 mm[25]。

试验台通过安装传感器直接采集刀具加工工件状态数据,以在铣刀完成一次走刀后测量其中的信号值。刀具在磨损测试期间的连续采样频率为50 kHz,每把刀具进行315次走刀测试,数据包括x,y,z三向铣削力信号、振动信号和声信号的均方根值。

5.2 信号处理

图5所示为对应刀具处于3个阶段振动信号的情形。在不同状态的振动信号中,初期磨损和正常磨损的振动信号比较平稳;剧烈磨损由于刀具表面金相组织遭到破坏,切削作业时的振动幅值明显增大,不同磨损状态信号有一定区别。EEMD能对信号进行自适应分析,因此本文采用EEMD与神经网络相结合对刀具磨损状态进行识别。

设置采样点数为2 048,包括初期磨损、正常磨损、剧烈磨损3种刀具状态信号,并对提取的信号进行EEMD处理,设置高斯白噪声与原始信号的标准差比值为0.2,根据式(5)计算得到总体平均分解次数为200,通过分解一共15个IMF,本文列出刀具各磨损状态的前3个IMF分量,如图6所示。

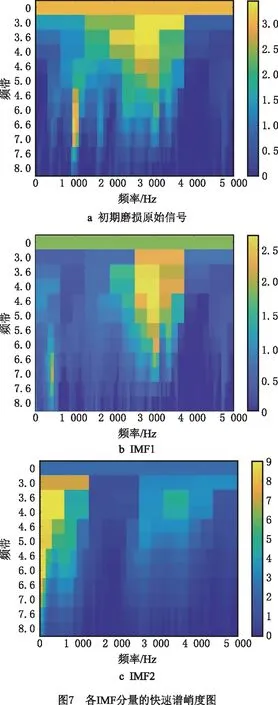
将EEMD信号分解得到3种状态IMF,采用快速谱峭度计算方法计算原始信号和IMF分量,并用快速谱峭度图表示,本文列出初期磨损原始信号与IMF1～IMF3的快速谱峭度图,通过最大谱峭度值所处的频带范围选取初期磨损信号中敏感的IMF分量,正常磨损与剧烈磨损两种磨损状态的分析方法与该方法相同。

对所提取的原始信号与IMF分量进行快速谱峭度计算并作快速谱峭度图,如图7所示。针对原始信号(如图7a),其快速谱峭度图中谱峭度最大值所在处的频带范围为箭头所指处(2 500,3 200)Hz,将该频带范围选定为信号特征频带区间;对比各IMF分量的快速谱峭度图与该原始信号快速谱峭度图的参数,由表1可知,IMF1的特征频带区间在原始信号频带区间,其余IMF的特征频带区间不在原始信号频带区间,因此选取IMF1为敏感IMF。

对所选取的IMF信号进行包络分析,以验证其是否具有真实性。如图8所示,与IMF2相比,进行包络分析后的IMF1包含了原始信号所具有的频率分量。

对筛选的IMF分量进行HHT变换得到Hilbert-Huang谱,刀具3种状态下得到的Hilbert-Huang谱如图9所示。在3种磨损状态中,正常磨损的时频分布范围集中在100 Hz～300 Hz,与初期磨损和剧烈磨损存在较大差别,初期磨损的时频范围与剧烈磨损的时频范围区别较大,且初期磨损的时频分布范围更加广泛。该方法能有效观察各磨损状态的时频分布,也为后续输入网络模型做准备。

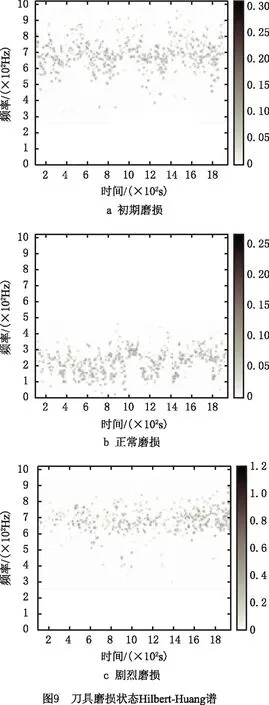
5.3 特征图片处理

生成的特征图存在图片规格不符、无用信息太多等情况,需要对得到的特征图进行预处理,如图10所示,具体包括:①去除Hilbert-Huang谱图中存在的坐标和能量条等多余信息;②对图片进行压缩,使其保持为256×256×3的图片,作为CNN神经网络的输入。

5.4 卷积神经网络的结构与超参数配置

本文在AlexNet神经网络基础上,对网络结构中的卷积核个数、卷积核大小、全连接层数与神经元个数进行修改。通过实验结果比对,最终确定的结构如表2所示。设置激活函数为Relu,优化器为Adam,损失函数为categorical_crossentropy。考虑本神经网络结构在训练过程中存在过拟合,本文在每层池化层之后添加Batchnormalization层并在全连接层添加AlphaDropout层,调整AlphaDropout为0.5。

表2 CNN模型参数

5.5 实验分析

考虑铣刀不同后刀刃存在磨损值干扰,本文将铣刀3个后刀刃的磨损平均值作为本次实验标签,如图11所示。刀具磨损状态分为3种,通过One-hot编码对3种状态进行标签转换,参数如表3所示。对每个状态的信号以2 048作为节点生成Hilbert-Huang谱图。由于获得的Hilbert-Huang谱图数量较多,本文对状态刀具随机采集600张Hilbert-Huang谱图,包括400张训练集、100张验证集和100张测试集。

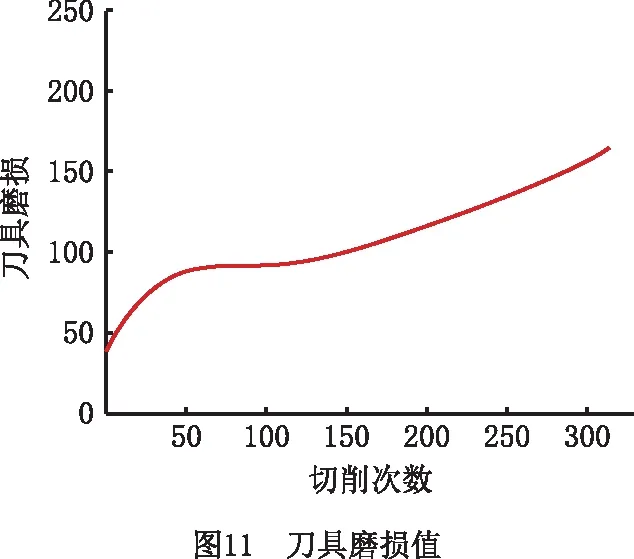
表3 刀具磨损状态参数表

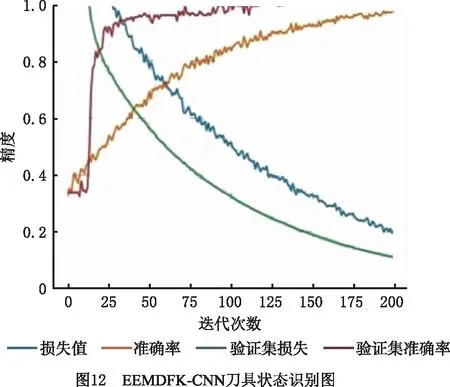
实验使用的硬件为AMD Ryzen71700X的CPU和GTX1660S的显卡,框架为Tensorflow 2.0,共进行200次迭代训练。如图12所示,训练集在第30次达到拐点,且准确率达到1,验证集准确率逐步上升最终达到98%,测试集准确率达到99.7%,损失值未出现振荡,模型未出现过拟合。利用已训练完成的网络模型在其他测试集上识别磨损状态,将模型判别结果以混淆矩阵的形式展示,如图13所示,Sort1,Sort2,Sort3分别代表3种不同的磨损状态,横坐标表示模型预测的磨损状态,纵坐标表示实际的磨损状态。本文选取50张刀具3种磨损状态特征图作为测试集来检验模型。由结果分析,该模型对识别不同刀具磨损状态的平均准确率达到99.7%,表明该方法能稳定识别刀具不同的磨损状态,具有良好的稳定性。

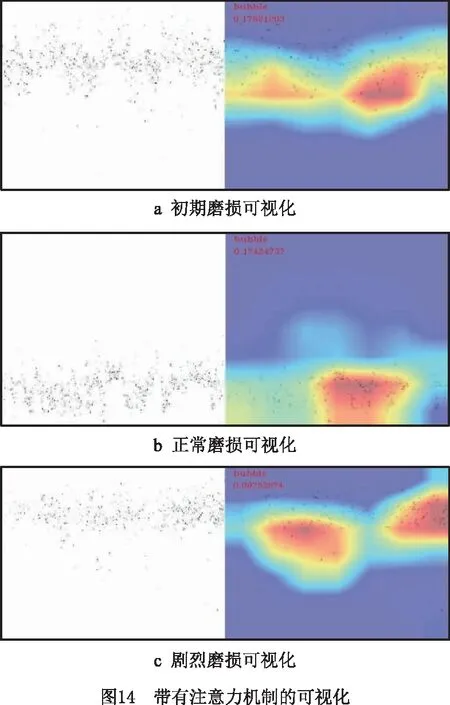
用热力图表示对图像卷积的可视化过程,以确定本文搭建的模型在图像识别中提取特征的效果。如图14和图15所示,在正常磨损中,带有注意力机制的模型与未添加注意力机制模块的模型虽然获取特征的效果相近,但是在初期磨损和剧烈磨损中,带有注意力机制的模型获取特征区域的效果明显,因此该模型效果更好。

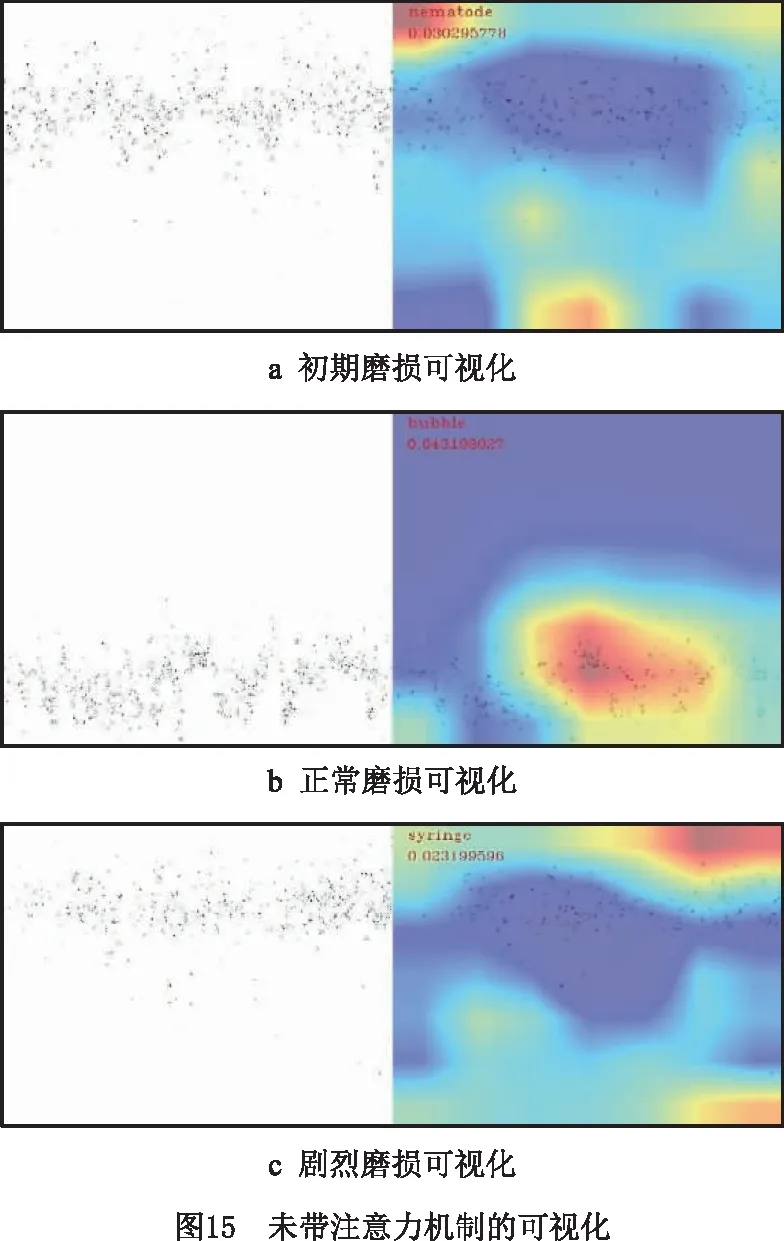
5.6 对比实验分析

本文将未经快速谱峭度(Fast Kurtogram,FK)算法筛选的EEMD-CNN方法进行对比分析,如图16所示。在正常磨损信号中,与传统筛选的IMF1相比,本文选取的IMF2包含更多真实信息;经过模型检验,EEMD-CNN方法存在明显的振荡现象,而且状态识别准确率比本文所提EEMDFK-CNN方案低6%,验证了本文方案具有一定的优越性。

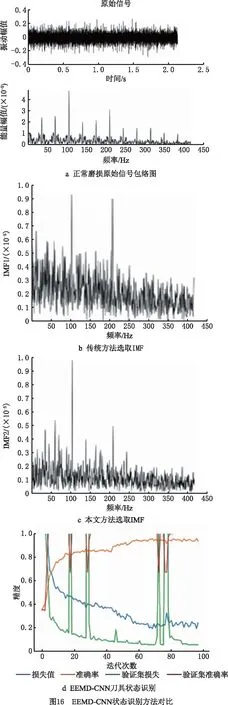
本文将EMDFK-CNN,Cmor3-CNN,EEMDFK-BP等模型与EEMDFK-CNN进行对比。在EMDFK-CNN,Cmor3-CNN中,设置CNN结构与上述EEMDFK-CNN结构相同,迭代次数为100,小波包分析选择Cmor3-CNN小波对信号生成时频图;EEMDFK-BP中,考虑图像尺寸问题,将图像缩减为28×28,设计三层BP网络结构,每层节点分别设置为128,56,32,识别结果如图17所示。

可见,EMDFK-CNN和EEMDFK-BP的迭代次数在30和15左右趋于平稳,但准确度与EMDFK-CNN相比较低,Cmor3-CNN模型振荡明显,存在过拟合现象,各方法的识别效果如表4所示。另外,本文对5种模型进行多次重复测试,每次得到的准确率如图18所示,充分说明EEMDFK-CNN方法具有更好的识别效果与稳定性。

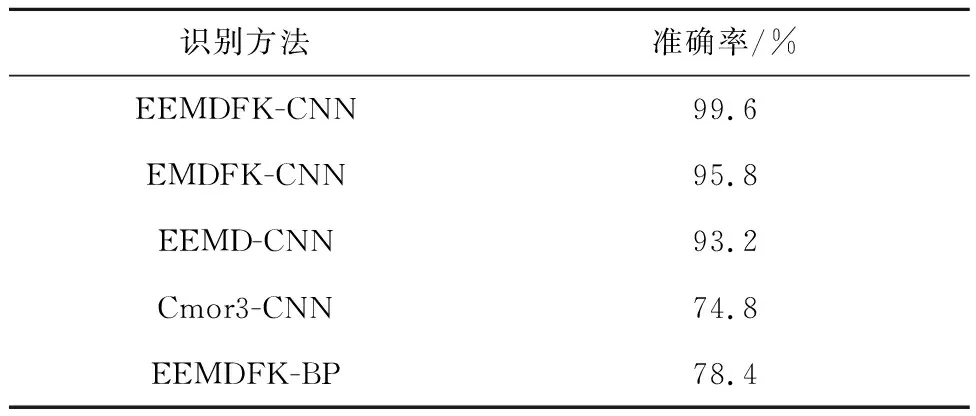
表4 各方法的识别效果

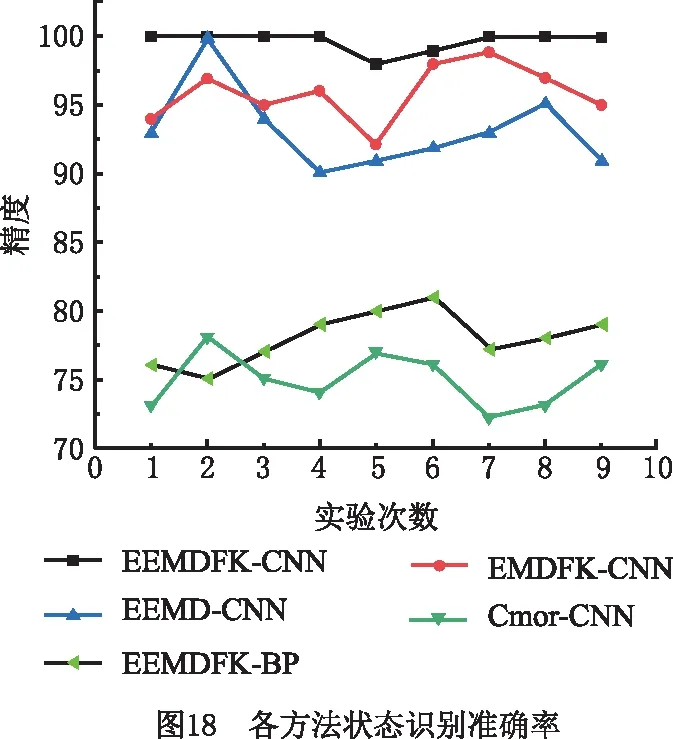
6 结束语

本文提出EEMDFK-ACNN刀具磨损状态识别方法,该方法是将刀具状态信号进行自适应时频分析,并提取相应的特征与深度学习结合的一种磨损状态识别方法。主要结论如下:

(1)与传统刀具磨损状态识别方法相比,采用EEMDFK和ACNN相结合的方法降低了依靠经验判断出现的失误,使识别效果更加智能化,而且通过实验验证,该方法更加方便高效。

(2)将EEMD-CNN,EMDFK-CNN,Cmor3-CNN,EEMDFK-BP 4种方法与EEMDFK-CNN进行对比分析,不同磨损状态下EEMDFK-CNN的识别效果均高于其他4种方法,证明了本文方法的有效性和鲁棒性。

由于EEMDFK-ACNN在迭代速度上相比其他4种方法并无优势,而且目前模型结构的建立大多依靠研究者的经验,超参数变化对磨损状态的识别效果影响较大,今后将对该方法的模型结构进行更深入地研究与优化。