面向设计众包的产品概念方案评价与选择
彭张林, 杜一甫, 程啸先, 唐孝安, 张 强
(1.合肥工业大学 管理学院,安徽 合肥 230009;2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)
0 引言
设计众包指企业在新产品开发过程中,基于互联网众包平台,利用外部广泛的社会化资源,寻求新产品设计的功能性解决方案的实践过程和创新模式[1-2]。Web 2.0和移动互联网技术加快了社交网络的发展,越来越多不同领域的用户通过众包等互联网平台与企业进行协同研发[3-5]。例如,波音通过Innocentive第三方众包平台及自身筹建的全球化协作体系吸引了约40个合作伙伴共同完成“787梦幻客机”的大部分设计工作[2];宝洁公司提出“联发”理念,通过在Yet2.com等众包网站上发布产品研发任务来提高公司的创新能力和研发生产力;Designboom作为全球设计行业中著名的众包平台,目前涵盖了工业、科技和建筑等多个领域,吸引了世界各地的优秀设计师在该平台上参与相关产品开发[6]。在此背景下,设计众包正逐渐发展为一种聚集丰富社会资源、依托社会化网络的新型商业模式,用户个性化需求及其自身设计理念不断深入到产品的开发过程中[7]。
一个完整的产品开发流程可以划分为“概念、计划、开发、验证、发布、迭代”6个阶段。一般而言,用户通过众包平台参与产品开发主要聚焦于概念阶段,如需求获取、关键技术识别、概念生成等前端工作[8],其中概念生成是将用户需求或设计理念转化为产品的功能特征与服务特征,并将这些特性映射到产品概念方案的结构化过程。产品概念方案通常采用草图和三维模型表示并附带简要的文字描述,其质量在一定程度上直接决定该产品是否满足用户需求以及商业化成功的可能性[9]。在设计众包过程中,企业将产品开发项目以众包任务的形式发布在众包平台上,用户通过自由自愿的形式进行投标并最终提交产品概念方案,发包方和平台需要基于一定规则从众多候选方案中选择符合任务需求的相对最优的方案,并给予中标用户相应的奖励。因此,产品概念方案评价与选择是设计众包整个服务流程中的关键环节,其合理性对产品开发项目的成功以及用户持续参与的意愿具有重要影响。
然而,与企业传统开发模式下由组织内部的专职研发人员依赖自身经验筛选相对有限的方案不同,设计众包环境下产品概念方案的评价与选择面临更大的复杂性,主要体现在:①设计众包环境下,大规模用户参与会涌现大量的产品概念方案,远超传统模式下企业内部研发人员设计出来的方案数量[6],这必将加大方案评价与选择的工作量和难度;②不同表达形式的产品概念方案是一种定制的知识创意型虚拟产品[1],其价值的测度和评价缺乏严谨客观的衡量标准,难以构建合理的评价指标体系;③产品概念方案中各评价指标间并非完全相互独立,彼此可能存在关联[10],在评价时应予以考虑;④设计众包环境下,用户需求与产品设计之间有了更多更深层次的直接交互[11],在方案选择过程中如何更好地考虑用户的需求偏好,对最终选出合理的方案至关重要;⑤产品概念方案评价过程中通常蕴含大量确定性和不确定性信息[12],在进行评价决策时如何集成这些不同维度、不同评价尺度和不同表达方式的信息也是一项重要的挑战。
1 评价模型
1.1 评价框架
针对设计众包环境下产品概念方案评价在初步筛选方案、构建评价指标体系、确定指标权重、考虑用户偏好以及融合集成确定性与不确定性信息等方面存在的复杂性,研究提出如图1所示的产品概念方案评价框架,该框架包括5个模块:
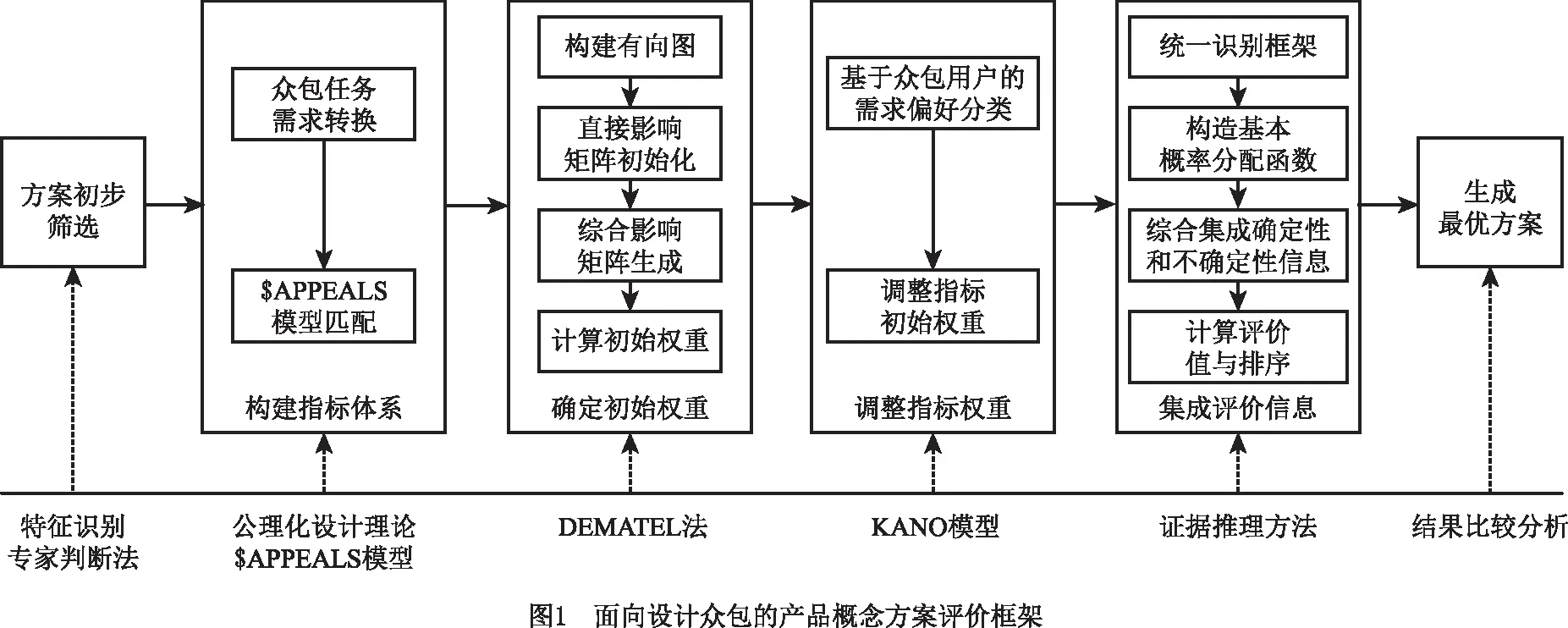
(1)初步筛选方案 在正式评估前,借助特征识别和专家判断的方法剔除某些设计明显无法满足基本要求的方案,形成候选方案列表。
(2)构建指标体系 根据公理化设计理论将设计众包任务的具体需求转换为产品的功能特征与服务特征,结合$APPEALS模型(又称成功产品的关键要素)确定概念方案评价指标。
(3)确定初始权重 考虑产品功能结构本身的紧耦合性,各评价指标之间存在一定程度的相互依赖和影响,因此采用DEMATEL法计算各指标的初始权重。
(4)调整指标权重 为了在概念方案评价和选择过程中更好地融合用户需求偏好,利用众包平台获取用户真实感知和偏好的便利性,在真实获取用户需求偏好的基础上,采用KANO模型调整各评价指标的权重,将用户需求的偏好信息直接反映在权值上。
(5)集成评价信息 发挥证据推理在融合确定性与不确定性信息上的优势,对各指标的评价信息进行综合集成,并完成候选方案排序,以生成最优方案供发包方选择。
整体上看,本文所提框架具有一定优势:①采用$APPEALS模型从众包任务需求特征、用户选择偏好两个维度综合确定评价指标,增强了选取指标的理论支撑;②各指标权重的计算更加贴合用户需求偏好,综合使用DEMATEL法与KANO模型,不但体现了各个指标间的内部关联关系,而且融入了用户的需求偏好特征;③考虑了评价过程的复杂性,评价信息存在模糊性、不确定性等,基于证据推理充分融合确定性与不确定性信息,获得被测对象的一致性解释或描述,从而有效处理不确定性多属性决策问题,更好地支撑发包方的优选决策。
下面详细介绍该评价模型的关键步骤。
1.2 基于$APPEALS模型的评价指标选取
在众包平台上,产品概念方案评价指标是对众包任务要求最直接的反映,而众包任务要求又源于产品最终要服务的用户和市场这一直接对象。对用户和市场需求的度量,一般采用经典的公理化设计理论,将用户需求转换为产品的功能性特征和服务性特征,在此基础上结合$APPEALS模型进一步解析和匹配产品设计的功能性和服务性需求。$APPEALS模型联系着市场和产品模型,可以将用户需求充分转换成产品的关键特性,从产品的价格($ Price)、可靠性(assurances)、性能(performance)、外观(packaging)、易用性(ease of use)、可获得性(availability)、生命周期成本(life cycle)和社会接受程度(social acceptance)8个维度定义了产品成功的关键要素。该模型可以用产品差异化雷达图表示,如图2所示。
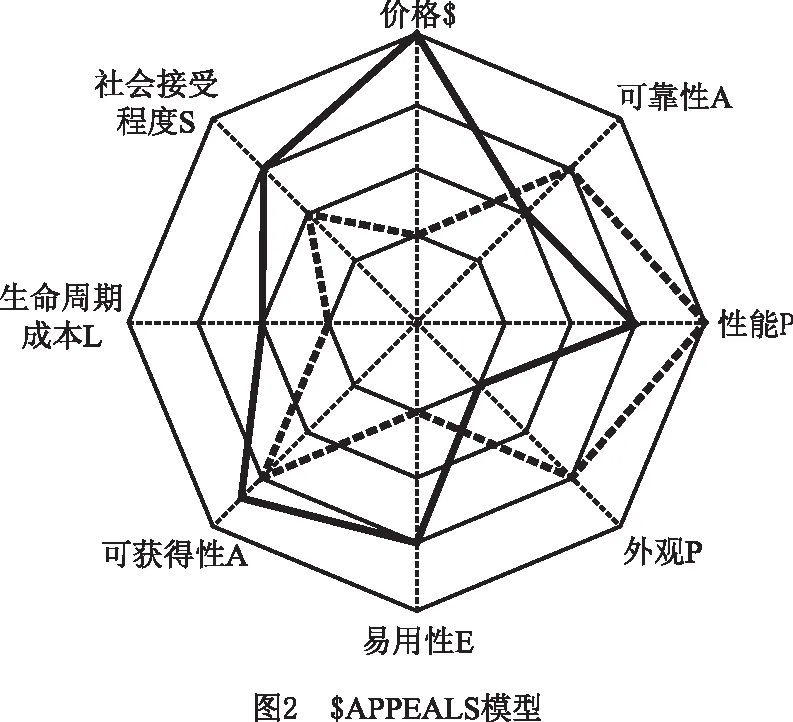
由图2可知,实线与虚线上的产品分别在价格和性能上更有优势,企业可以根据自身定位选择合适的细分市场有针对性地开发产品。假设经过对用户提交的全部方案进行初步筛选后还有M个候选方案,评价指标有n个,则方案集为A={al|l=1,2,…,M},评价指标集为G={Gi|i=1,2,…,n}。
1.3 基于DEMATEL法的指标权重的初始确定
DEMATEL法由日内瓦Battelle协会的Fontela和Gabus两位教授提出,该方法基于图论构建可视化的结构模型以认知并评估复杂因素之间的相互依赖关系[24]。利用该方法计算指标初始权重的步骤如下:
(1)构建直接影响矩阵X=[xij]n×n。邀请领域专家辨析各个指标之间的影响程度并打分,其中Gi对Gj的影响值记为xij(i≠j),本文采用五分点法,即xij的值可能取0,1,2,3,4,分别对应无影响、低影响、中影响、高影响和极高影响,当i=j时令xij=0。
(2)规范化直接影响矩阵得到Y=[yij]n×n,其中
(1)
(3)计算各个指标的中心度。将规范化后的直接影响矩阵转化为综合影响矩阵T=Y(I-Y)-1=[tij]n×n,基于矩阵T,分别计算各行元素与各列元素之和:
(2)
式中:Tr(i)为影响度,即指标Gi对其他指标的影响之和;Tc(i)为被影响度,即指标Gi受其他指标的影响之和。则指标Gi的中心度
mi=Tr(i)+Tc(i)。
(3)
(4)计算各个指标的初始权重。指标Gi的权重
(4)
1.4 基于KANO模型的指标权重调整
狩野纪昭教授于1984年提出KANO模型[25],他认为对质量的认知要从一维模型细化到二维模型,即用户的主观感受和产品/服务的客观表现。该模型根据不同的产品特性与用户满意度之间的关系,将用户需求偏好信息分为基本型需求(M)、期望型需求(O)、魅力型需求(A)、无差异型需求(I)和反向型需求(R)5类[26],如图3所示。
发挥众包平台获取用户需求的便利性,结合文献[22]的KANO模型分类评估表,确定各评价指标对应归属为A,O,M,I,R中的某个类别,从而调整权重,具体步骤如下:
(1)确定各指标权重的调整系数 借鉴文献[22]的研究,将A,O,M,I各类评价指标对应的调整系数定义为4,2,1,0。
(2)计算最终权重 根据调整系数,指标Gi的最终权重为
(5)
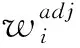
1.5 基于证据推理的评价信息综合集成
证据推理首先由Dempster提出,然后由Shafer等进一步完善。该方法利用概率的半可加性原则代替可加性原则,使证据合成后的不确定性度量仍然满足单个证据基本可信数的性质,保证证据的信念合成具有系统完整性,度量结果更贴近真实[27]。运用证据推理融合产品概念方案中的确定性信息和不确定性信息的主要步骤如下:
(1)构造统一评价集
1)指标的分布评价变换
当指标为定性指标时,其分布评价常根据决策者的经验知识确定,不同情况下分布不同。本文主要探讨定量指标的分布评价变换。
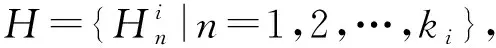
(6)
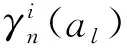

(7)
2)不同评价集的转换
统一的评价集是信息集成的前提,当不同指标的评价集有差异时,根据文献[27],将评价集Θ=(H1,…,Hi,Hi+1,…,Hu)映射到统一评价集H=(H1,H2,…,Hi,…,Hk),如图4所示。
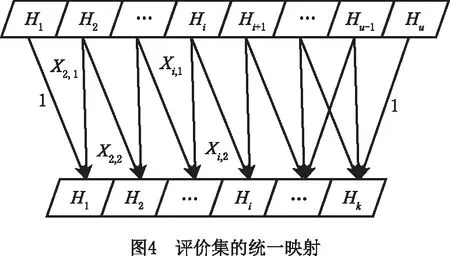
该映射方法有以下特点:①Θ中任一评价等级映射在H上评价等级为Hi的比例均在[0,1]之间,且分配到不同评价等级的比例之和为1;②Θ映射在H上评估等级为Hi的值为Θ上不同评价等级的映射之和,如H中的H1等于Θ上的H1+X2,1H2。
(2)确定概率分配函数
1)确定各指标的分布评价
假设评价指标体系有两层指标,即基本指标G={G1,…,Gn}和上层指标y,统一评价框架为H=(H1,…,Hk,…,HK),令H1H2…HK,其中表示劣于,指标的权重值为对于∀al∈A,方案al下指标Gi在统一评价框架下的分布评价为
S(Gi(al))={(Hk,βk,i(al))|k=1,2,…,K;
i=1,2,…,n;l=1,2,…,M}。
(8)
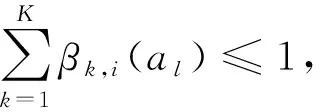
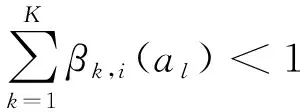
(9)
2)构造概率分配函数
令mk,i(al)为已分派的概率分配函数,表示方案al下Gi指标支持上层指标y为等级Hk的程度,
(10)
式中k=1,2,…,K。
mH,i(al)为未分派的概率分配函数,表示方案al下Gi指标未支持上层指标y为任何等级,
(11)
可将mH,i(al)进一步分解,即
(12)

(13)
(3)集成多源评价信息
对于∀al∈A,令I(i)为集成方案al前i个基本指标,mk,I(i+1)(al)为方案al前i+1个基本指标集成后支持上层指标y为等级Hk的程度,mH,I(i+1)(al)为方案al前i+1个基本指标集成后未支持上层指标y为任何等级的程度。在递归起点,令:
(14)
则有:
(15)
式中KI(i+1)(al)为规模化因子,反映不同证据之间矛盾的大小,
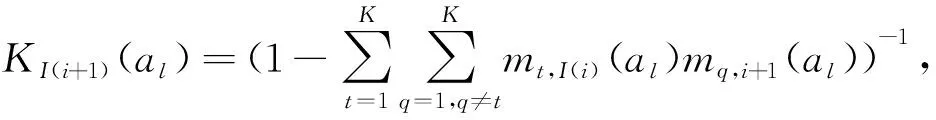
(16)
集成所有基本指标后,计算上层指标y的综合信任度,对于∀al∈A,有:
(17)
式中:βk(al)为方案al在上层指标y下被评为等级Hk的置信度;βH(al)表示方案al在上层指标y下未被评为任何等级,即信息无知度。由此可得方案al的分布评价
S(y(al))={(Hk,βk(al))|k=1,2,…,K;
l=1,2,…,M}。
(18)
实际上,对于多层指标,可以将此时的上层指标当作基本指标,通过同样的方法集成。
(4)计算综合效用并排序
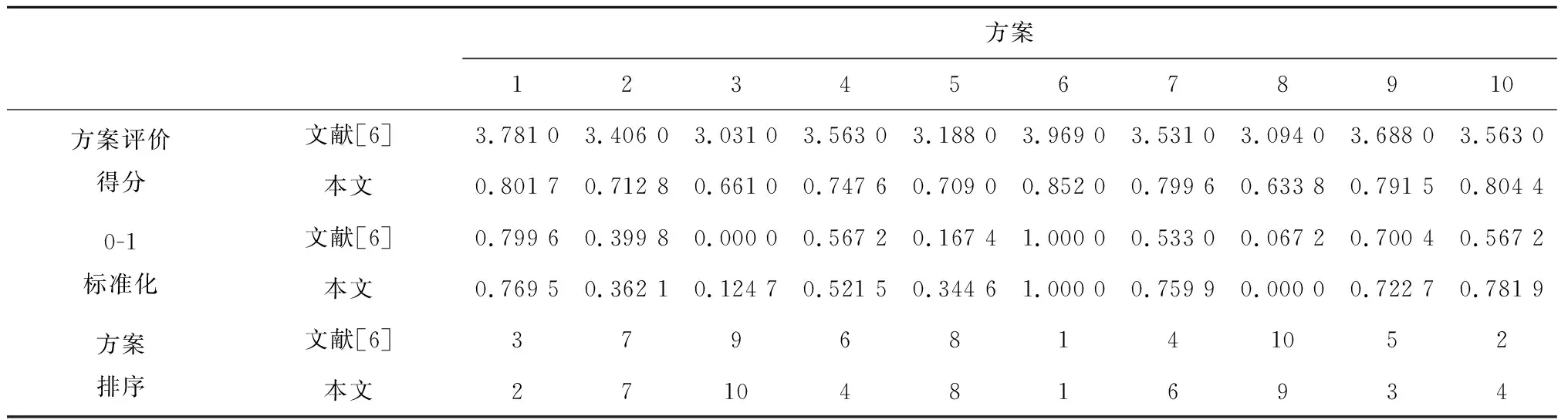
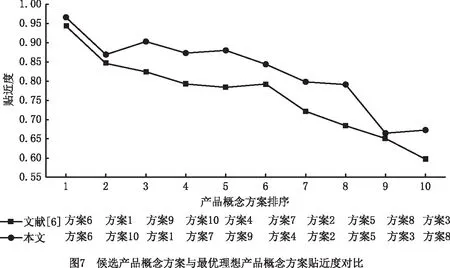
设评价框架H=(H1,…,Hk,…,HK)中不同评价等级Hk对应的效用为u(Hk),通常令u(H1) (19) 当对方案al进行完全评价,即βH(al)=0时,有umax(al)=umin(al)=uave(al)。 最后通过平均效用对备选方案排序,则对于∀al,av∈A,有: alav⟺uave(al) (20) 式中~为“无差异于”。 本文选取Design Boom众包平台上的未来个人计算机(Personal Computer,PC)方案设计任务作为案例进行研究,该任务由日本富士通公司发布,最终收集了1 000余份计算机设计方案。富士通公司成立了包括本公司的高级副总裁、设计中心总经理和外部知名工业设计大师等的专家评审团队,该团队从1 000多个设计方案中初选了108个方案。文献[6]基于108个方案进一步筛选出10个方案,如表1所示。在此基础上,本文根据上述搭建的产品概念方案评价模型进行评价,并与文献[6]的评选结果进行对比。 表1 10个候选方案的基本信息 2.2.1 建立PC产品概念方案的评价指标体系 为了提高概念方案与用户市场的匹配度,体现其商业成功的关键决定性因素,本文结合$APPEALS模型,对文献[6]选取的“人机交互性”“创新性”“灵活性”“可靠性”4个评价指标进行扩展,新增了“可制造性”和“外观时尚性”两个指标,分别对应$APPEALS模型中的可获得性和外观特征。因为对于PC产品概念方案,其设计可制造性的高低直接决定企业是否采纳,是十分重要的指标,同时PC产品最终要面向客户,当下的社会环境,客户对PC产品的外观要求可能比较高,因此也应考虑时尚性指标,各指标的评价集如下: 根据专家判断并结合文献[6]的部分数据,最终得到各个方案的指标值,如表2所示。 表2 方案评价值 2.2.2 基于DEMATEL法的初始权重确定 首先邀请专家辨析评价指标的相互影响,并根据专家意见绘制指标关联关系有向图,如图5所示;然后构建各评价指标的直接影响矩阵,如表3所示。 表3 初始直接影响矩阵 由式(1)~式(4)计算出G1~G6的权重分别为0.24,0.16,0.19,0.10,0.18,0.13。 2.2.3 基于KANO模型的权重调整 针对富士通公司发起的众包任务和10个候选方案,设计KANO问卷并发放至Design Boom平台,最终收集了173份有效问卷,根据频数最大优选法原则得到各个指标的分类结果,如表4所示。 表4 用户需求偏好分类表 根据式(5)调整指标权重,计算出G1~G6调整后的权重分别为0.14,0.10,0.23,0.12,0.11,0.30。 2.2.4 基于证据推理的评价信息集成 首先根据式(6)和式(7)得出方案al关于评价指标Gi在评价集Hi的分布评价,以方案1为例: 其次将不同的评价集映射到统一评价集下,设统一评价集H={H1,H2,H3,H4,H5},映射规则如图6所示,得出方案al下评价指标Gi在H的分布S(Gi(al))。 例如对于方案1,在H上,其分布为: S(G1(a1))={(H3,0.05),(H4,0.5),(H5,0.45)}; S(G2(a1))={(H3,0.13),(H4,0.5),(H5,0.37)}; S(G3(a1))={(H2,0.04),(H3,0.29), (H4,0.46),(H5,0.21)}; S(G4(a1))={(H4,0.47),(H5,0.53)}; S(G5(a1))={(H4,0.46),(H5,0.54)}; S(G6(a1))={(H2,0.05),(H3,0.15),(H4,0.45), (H5,0.35)}。 然后,基于式(8)~式(18)对评价信息进行融合集成,得到10个方案在H上的分布评价分别为: S(y(a1))={(H1,0),(H2,0.021 2), (H3,0.12),(H4,0.489 6),(H5,0.369 2)}; S(y(a2))={(H1,0.008 1),(H2,0.081 4), (H3,0.2),(H4,0.472 3),(H5,0.238 2)}; S(y(a3))={(H1,0),(H2,0.132 4), (H3,0.294 9),(H4,0.368 9),(H5,0.203 8)}; S(y(a4))={(H1,0),(H2,0.031 8), (H3,0.185 9),(H4,0.542 5),(H5,0.239 8)}; S(y(a5))={(H1,0.003),(H2,0.053 4), (H3,0.232 8),(H4,0.526 3),(H5,0.184 5)}; S(y(a6))={(H1,0),(H2,0.038 1), (H3,0.109 5),(H4,0.437 8),(H5,0.414 6)}; S(y(a7))={(H1,0),(H2,0),(H3,0.123 6), (H4,0.554 4),(H5,0.322)}; S(y(a8))={(H1,0),(H2,0.090 8), (H3,0.404 7),(H4,0.382 9),(H5,0.121 6)}; S(y(a9))={(H1,0),(H2,0.028 5), (H3,0.133 2),(H4,0.482 2),(H5,0.356 1)}; S(y(a10))={(H1,0),(H2,0.005 3), (H3,0.144 6),(H4,0.477 2),(H5,0.372 9)}。 设各评价等级的效用分别为u(H1)=0,u(H2)=0.25,u(H3)=0.5,u(H4)=0.75,u(H5)=1。由式(19)计算对应10个方案的效用值为:u(a1)=0.801 7,u(a2)=0.712 8,u(a3)=0.661 0,u(a4)=0.747 6,u(a5)=0.709 0,u(a6)=0.852 0,u(a7)=0.799 6,u(a8)=0.633 8,u(a9)=0.791 5,u(a10)=0.804 4。由此可知,这10个方案的排序为a6≻a10≻a1≻a7≻a9≻a4≻a2≻a5≻a3≻a8。 本文与文献[6]的评价结果对比如表5所示,其中选出的最优方案均为方案6,但是后续排序不同,主要原因在于评价指标选取不同、权重的确定方法不同以及信息融合的方法不同。 表5 本文与文献[6]评价结果的对比 为了进一步证明本文所提方法的有效性,利用候选产品概念方案与最优理想产品概念方案的贴近度AC来衡量评价结果的质量[29]:每个候选产品概念方案都可以看作是多维空间中的一个点,这个点与最优理想点距离越近,贴近度越高,该候选产品概念方案的质量越高。AC的表达式为 (21) (22) 式中:Cli为方案al下第i个指标Gi标准化处理前的初始评价值;Ci,max,Ci,min分别为所有方案中指标Gi的最大、最小初始评价值。 文献[6]中各指标的评价值均为点值,标准化处理比较方便。而本文的指标评价值均采用分布评价S(Gi(al)),标准化处理存在一定困难,为此设不同评价等级所对应的数值依次为H1=0,H2=0.25,H3=0.5,H4=0.75,H5=1,结合各评价指标在各评价等级下的概率分布将评价值转化为点值,再进行标准化处理。最后基于式(21)计算各候选产品概念方案与最优理想产品概念方案的贴近度,本文与文献[6]的对比结果如图7所示。 由图7可知,在同一排名下,采用本文评价模型得出的方案与最优理想产品概念方案的贴近度均比文献[6]高,说明本文构建的产品概念方案评价模型更具优越性,其原因如下:①评价指标选取具备理论支撑,即在文献[6]的基础上结合$APPEALS模型新增可制造性和时尚性两个指标,增加了对设计可制造性和外观视觉特征的测量;②指标权重计算更加合理,文献[6]为简化计算,直接将权重平分至各个指标,没有考虑指标的差异性,而本文利用DEMATEL法和KANO模型,不但考虑到指标间的内部影响关系,而且进一步融入了用户的需求偏好,更好地发挥了用户这一主体的话语权;③评价信息更加真实客观,文献[6]通过专家评价法以0~5分制作为评分体系对各项指标进行打分,本文较多地考虑了评价信息中存在的模糊性和不确定性,并利用证据推理在融合确定性和不确定性信息上的优势,将这些多源信息映射到同一评价集下,进而得出综合效用,使评价结果更贴近实际。 除此之外,针对该案例,引入TOPSIS方法[29-30],首先用向量规范法求得规范决策矩阵,由此确定正理想解与负理想解,再计算各方案到正理想解与负理想解的加权距离,最后基于距离测度相似度C进行排序: (23) 当权重设置与本文相同时,评价结果为a6≻a7≻a10≻a1≻a9≻a4≻a3≻a5≻a2≻a8,与本文评价结果不同,主要原因是该方法并未考虑评价过程中存在的模糊性和不确定性等因素;当不考虑指标间的权重差异时,求得评价结果为a6≻a1≻a9≻a7≻a10≻a4≻a2≻a5≻a8≻a3,对比可知该评价结果与文献[6]的评价结果基本一致,而与本文评价结果存在一定差异,这是由于TOPSIS方法并未考虑指标间的影响与用户的需求偏好,该评价模式只适用于初期没有经验的众包用户。 企业利用设计众包开展产品开发不但可以超越企业组织内部个体能力的局限,实现碎片化知识的整合和集成,而且有利于突破传统思维定势,开展突破性创造和颠覆式创新。然而,与企业传统开发模式下产品概念方案评价不同的是,设计众包环境下产品概念方案的评价与选择在评价指标体系构建、指标权重确定、用户偏好的考虑以及确定性与不确定性信息融合等方面面临更大的复杂性。因此提出一种面向设计众包的产品概念方案评价与选择模型,首先根据特征识别和专家判断法初步筛选方案,以减轻发包方审查大量产品概念方案的负担;其次通过$APPEALS模型从众包任务需求特征、用户选择偏好两个维度建立产品概念方案的评价指标体系;然后考虑到指标间的影响关系及用户需求偏好,利用DEMATEL法与KANO模型计算指标;最后基于证据推理构造统一的评价集,通过递归算法实现证据的综合集成,完成对概念方案的排序与优选。最终以Design Boom众包平台上的计算机方案设计任务为例,验证了所提模型的可靠性和有效性。未来的研究可以进一步简化该评价模型的算法,或引入人工智能算法,在保证评价结果质量的同时提高决策效率。2 案例研究
2.1 案例描述

2.2 评价计算
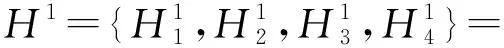
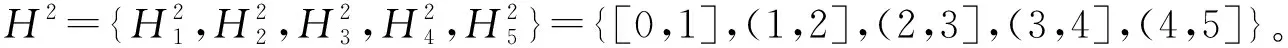
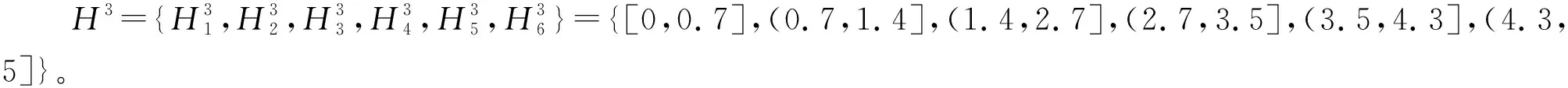
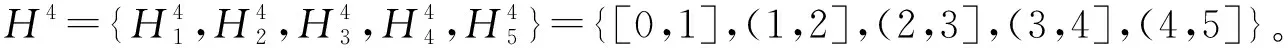
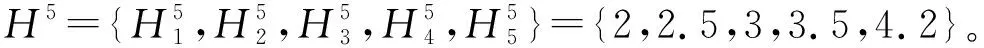
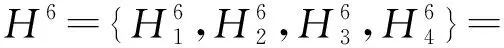
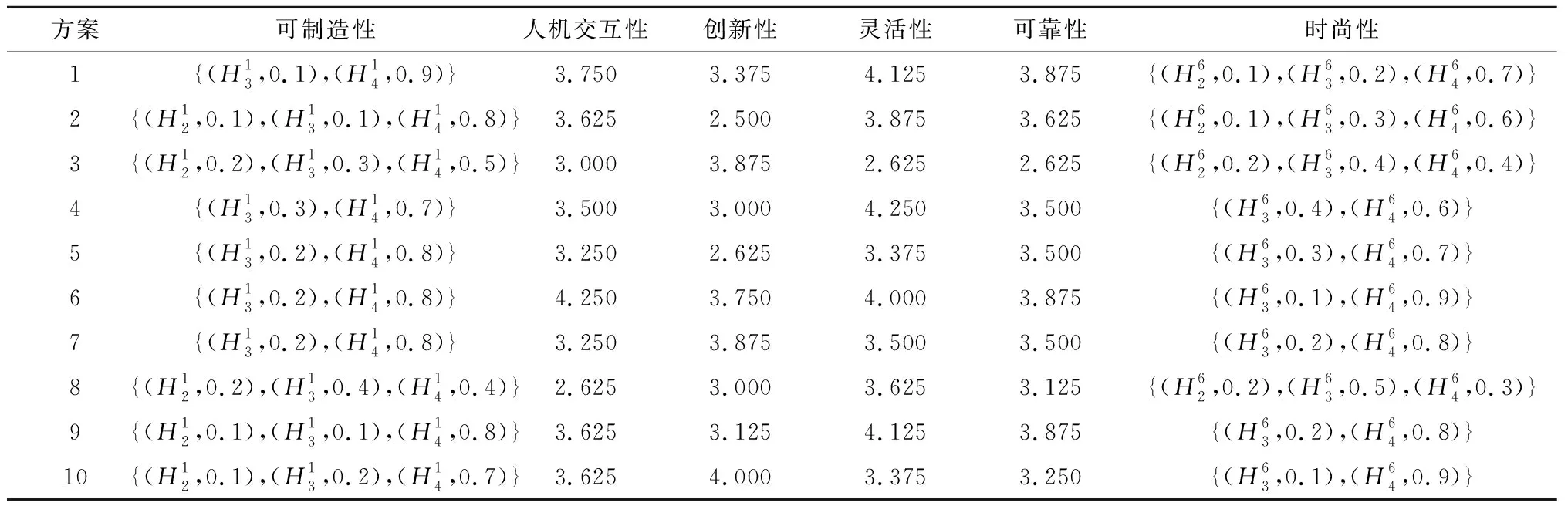
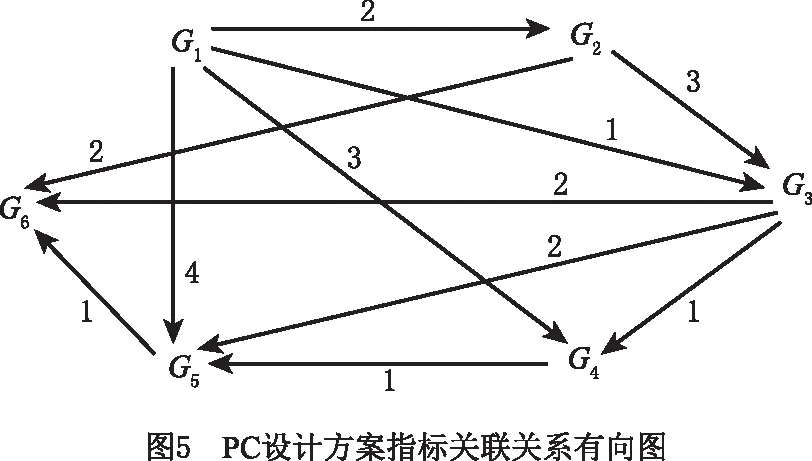
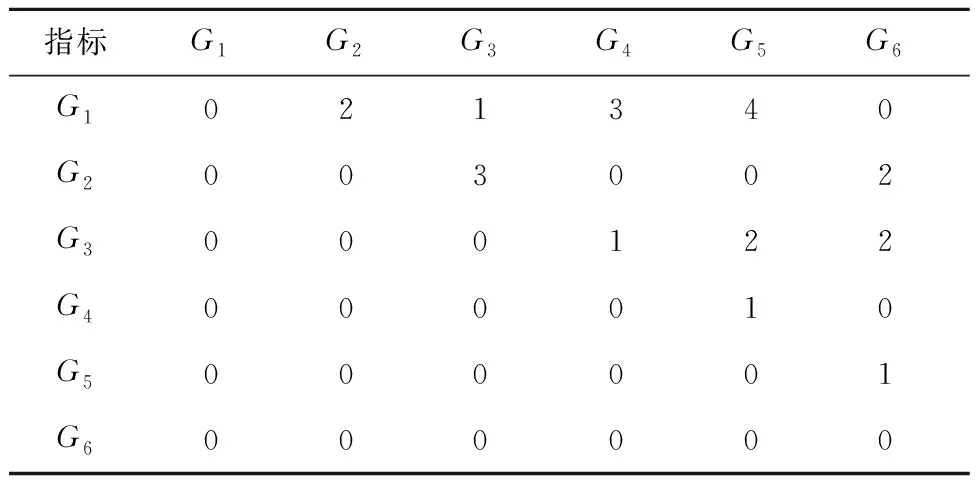
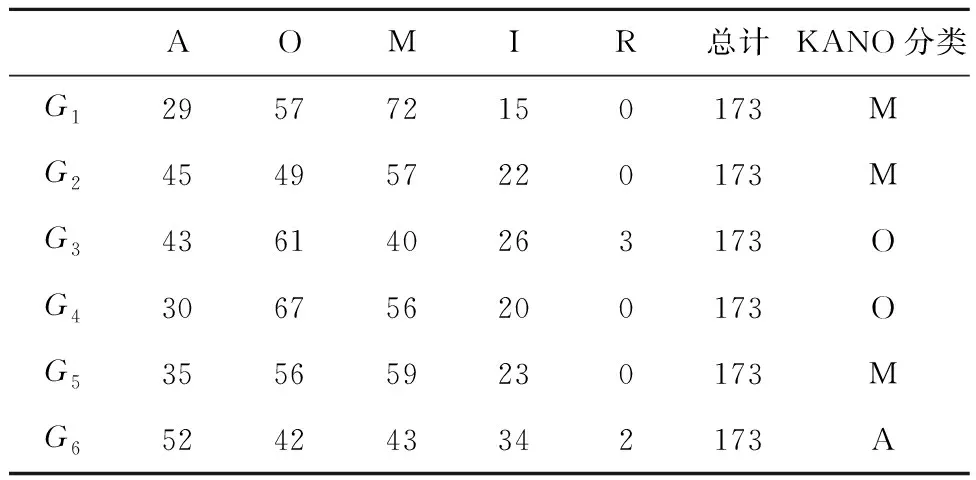
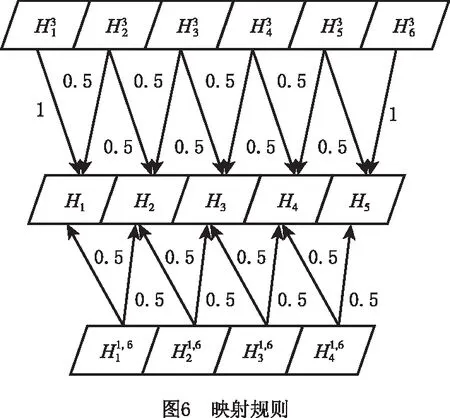
2.3 结果对比分析

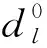
3 结束语

