改进型免疫克隆布谷鸟算法求解软后坐火炮多参数辨识

赵 伟,侯保林,鲍 丹

(1.南京理工大学 机械工程学院,南京 210094;2.南京理工大学 瞬态物理国家重点实验室,南京 210094)

火炮软后坐技术是一种减小火炮发射后坐力的专项新技术。(常规火炮在发射过程中伴随有剧烈的冲击与振动现象,与常规火炮不同,软后坐火炮是在后坐部分向前运动的过程中进行击发,这种击发模式利用火炮的前冲动能抵消了部分后坐能量,不仅减小火炮发射过程中的后坐力,而且同时减小火炮发射过程中的冲击与振动。为进一步研究软后坐火炮发射过程的运动特性,对其进行大量试验来研究发射过程的运动特性是十分不经济的,因此采用构建动力学模型进行数值仿真及试验数据修正的方法来研究软后坐火炮发射过程中的动力学特性是十分有优势的且已经成为了首要方法[1]。但是由于软后坐火炮的复杂结构,其发射过程的动力学模型中存在大量的未知参数,并且这些未知参数的选取决定了所建立动力学模型与实际系统的相似程度和准确程度,因此如何准确的确定这些未知参数成为了关键问题。传统的、单一的优化算法在多参数辨识问题上的求解存在辨识精度低的现象。近些年发展出来许多辨识算法和策略来提高辨识效果。文献[2]采用改进粒子群算法进行参数辨识,提高辨识精度;文献[3]提出自适应混沌变异粒子群优化辨识方法,提高了辨识效率,缩短计算时间;但是上述算法并不能高效求解发射过程种的多参数辨识问题。

为求解软后坐火炮发射过程的多参数辨识问题,本文提出了一种适用于求解多参数辨识问题的算法,即改进型免疫克隆布谷鸟算法(improved immune clone cuckoo algorithm,IICCA)。免疫克隆选择算法是基于免疫系统的克隆选择理论发展出来的一种智能算法[4]。基于免疫克隆选择算法的种群刷新操作和克隆操作,该算法在求解多参数寻优问题上具有明显优势[5-6]。但是传统的免疫克隆算法存在计算量大、后期收敛速度慢、存在冗余迭代等缺点。引入其他的选择策略,结合其他算法的优势,可有效进一步提高免疫克隆选择算法的优越性。

本文针对免疫克隆选择算法克隆种群多样性低的问题,在更新过程中引入随机杂交策略和高频变异[7],提高克隆种群的局部搜索能力。针对传统免疫克隆选择算法变异概率为固定值,算法不易取得最佳概率值的问题,引入了文献[8]的自适应算子,自适应算子增强了计算初期的全局搜索能力与计算后期的局部搜索能力。针对冗余计算的问题,引入精英抗体的提取算子,提高了计算效率。针对算法收敛速度慢的问题,引入疫苗接种策略[9]来提高算法的收敛速度,对疫苗接种后的抗体种群采用Lévy飞行策略和巢寄生行为[10]进行二次搜索,提高疫苗接种后种群的多样性,从而避免由于疫苗接种策略导致的抗体种群多样性下降而陷入局部最优。同时Lévy飞行相比其余随机搜索具有更优秀的全局搜索能力[11],在疫苗接种后的高质量抗体群的基础上进行全局搜索,更加有利于种群向最优解附近聚集。并且巢寄生行为本质上是一种局部搜索行为,在高质量的种群基础上进行局部搜索,更加利于算法收敛。布谷鸟算法相比粒子群优化算法与遗传算法具有更高的搜索效率[12],因此将免疫克隆选择算法与布谷鸟算法相结合比与其他算法结合将具有更高的求解效率。为验证改进后算法的有效性,选用5个多峰测试函数对其进行验证,将IICCA与免疫克隆选择算法(immune clone select algorithm,ICSA)、免疫遗传算法(immune genetic algorithm,IGA)[13]、自适应粒子群算法(adaptive particle swarm optimizer,APSO)[14]和改进型布谷鸟算法(improved cuckoo search,ICS)[15]进行寻优性能对比测试。

本文对软后坐火炮发射过程进行动力学分析,建立软后坐炮在发射过程中的动力学模型。在此基础上,对动力学模型中的多参数采用IICCA算法进行辨识,并与其他4种辨识算法进行收敛速度和精度的比较,验证IICCA算法在求解软后坐火炮发射过程多参数辨识问题的有效性和准确性。

1 软后坐火炮发射过程的动力学模型建立

1.1 后坐部分运动方程

软后坐火炮的后坐缓冲装置由两个制退机和两个前冲机组成。设定炮口方向为正方向,其后坐部分发射过程的运动方程为

mgsinθ-Fpt

(1)

式中：Fq为前冲机力;Fz为制退机力;Ff为由于密封装置,前冲活塞杆与制退杆所受到的摩擦力总和;x为后坐部分的位移;sign(·)为符号函数;m为后坐部分的质量;θ为火炮射角;μ为导轨摩擦因数;Fpt为炮膛合力。

1.2 前冲机动力学模型建立

前冲机共有两类腔室,分别为气体腔和液体腔。其中,液体腔又分为液体腔Ⅰ、液体腔Ⅱ和液体腔Ⅲ,前冲机结构如图1所示。前冲机的运动形式为杆后坐形式,即前冲活塞杆随炮身一起运动。

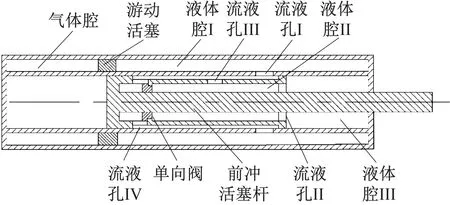
图1 前冲机结构示意图

前冲机力由液体腔Ⅲ的液体压强提供,因此前冲机力的方程如式(2)所示

Fq=2pqAq

(2)

式中：pq为液体腔Ⅲ的压强;Aq为前冲活塞的面积。

(1) 前冲过程：记图1中前冲活塞杆的活塞尾端与流液孔Ⅰ之间的距离为L。当前冲位移x小于L时,气体腔的压缩气体向右推动游动活塞,液体腔Ⅰ中液体经由流液孔Ⅰ和流液孔Ⅲ进入液体腔Ⅱ,然后经由流液孔Ⅱ进入液体腔Ⅲ,从而推动前冲活塞向前运动。分别列出前冲位移小于L时液体流经流液孔Ⅰ、流液孔Ⅱ、流液孔Ⅲ时的伯努利方程如下

(3)

式中：vq1为液体在流液孔Ⅰ的绝对速度;vq2为液体在流液孔Ⅱ的绝对速度;vq3为液体在流液孔Ⅲ的绝对速度;py为液体腔Ⅰ的液体压强;pq为液体腔Ⅲ的液体压强;p1为液流流经流液孔Ⅰ后的压强;p2为液流流经流液孔Ⅲ后的压强;ρ为液体密度;ξq1,ξq2,ξq为前冲距离小于L时液体流过流液孔Ⅰ、流液孔Ⅱ、流液孔Ⅲ的能量损失系数。

根据连续性方程计算流各液孔的流速。

(4)

将式(3)、式(4)联立即可求得前冲位移小于L时液体腔Ⅲ的压强。

(5)

式中：Kq1为前冲位移小于L时液体流过流液孔Ⅱ的液压阻力系数,且Kq1=ξq+1;Aq1～Aq3分别为流液孔Ⅰ～流液孔Ⅲ的面积;Ay为游动活塞工作面积。

由于液体腔Ⅰ的压强py仍是未知,因此需要对py进行求解。根据气体腔的状态方程、游动活塞的牛顿运动定律以及液体连续性方程推导液体腔Ⅰ的压强如式(6)所示。

(6)

式中：n为气体腔的气体非线性指数;fy为游动活塞与筒壁的摩擦力;my为游动活塞的质量;lq0为气体腔的初始长度;p0为气体腔压强。

当前冲位移x>L时,液体腔Ⅰ中的液体直接流经流液孔Ⅰ进入液体腔Ⅲ。此时液体腔Ⅲ中压强的公式推导与式(5)同理。此处推导过程省略,液体腔Ⅲ的压强为

(7)

式中,Kq2为前冲位移大于L时液体流过流液孔Ⅰ的液压阻力系数。

软后坐火炮的复进过程与前冲过程前冲机的运动一致,方程完全相同,因此不再赘述。

(2) 后坐过程：当后坐运动刚开始时,后坐部分的位移x仍大于L,所以此时在前冲活塞的推动下,液体腔Ⅲ中的液体直接流经流液孔Ⅰ进入液体腔Ⅰ。根据伯努利方程与连续性方程推导出液体腔Ⅲ的压强为

(8)

式中,Kq3为后坐位移大于L时的液压阻力系数。

当后坐一定距离,即后坐部分位移x

(9)

式中：Kq4为后坐位移小于L时,液体流过流体孔Ⅰ的液压阻力系数;ξq3,ξq4为后坐位移小于L时,液体流过流体孔Ⅱ、流体孔Ⅳ的能量损失系数;Aq4为流液孔Ⅳ的面积。

1.3 制退机动力学模型建立

制退机由液体腔Ⅰ和液体腔Ⅱ两个腔室组成,具体如图2所示。制退机的运动形式为杆后坐形式,即制退杆随炮身一起运动。

图2 制退机结构示意图

制退机方程的假设条件与前冲机一致。制退机力由液体腔Ⅰ和液体腔Ⅱ的液体压强差提供,因此制退机力的方程为

(10)

式中：Δpz为液体腔压强差;Az为制退活塞的面积。

(1) 前冲过程：液体腔Ⅰ中的液体受到挤压,单向阀处于打开状态,液体腔Ⅰ中的液体分两股液流分别流入液体腔Ⅱ。一股经单向阀的活塞口流入液体腔Ⅱ,另一股经由筒壁沟槽流入液体腔Ⅱ。由于筒壁沟槽流口与单向阀流口的面积比接近于1∶1,因此为简化计算,采用平均流速进行等效。根据伯努利方程推导制退机内部产生的压强差如下

(11)

式中：Kz1为前冲过程制退机的液压阻力系数;Az1为沟槽的流口面积;Az2为单向阀的流口面积。

(2) 后坐过程：单向阀关闭,此时液体腔Ⅱ中的液体只能经由筒壁沟槽流入液体腔Ⅰ。筒壁沟槽在后坐部分位移x>0时是等齐沟槽,但当后坐位移x<0时,筒壁沟槽是斜坡形状。后坐过程制退机内部产生的压强差如式(12)所示

(12)

式中：Kz2,Kz3为后坐过程液体流经筒壁沟槽的液压阻力系数;K为制退机斜坡沟槽的形状比例系数。

(3) 复进过程：此时制退机内部液体流动状态与前冲过程相同,但复进过程中的沟槽为斜面沟槽。

(13)

式中,Kz4为复进过程制退机的液压阻力系数。

2 软后坐火炮发射过程参数辨识问题描述

2.1 软后坐火炮待辨识参数描述

后坐部分运动方程中需要辨识的参数有导轨摩擦因数μ和前冲活塞杆与制退杆所受到的摩擦力Ff,参数μ和Ff的数值正确与否影响着火炮发射过程中能量损失项的计算准确性。

前冲机方程中的待辨识参数包括：前冲机的液压阻力系数Kq1,Kq2,Kq3,Kq4,前冲机的损失系数ξq1,ξq2,ξq3,ξq4,气体非线性指数n以及游动活塞的摩擦力fy。前冲机的液压阻力系数和能量损失系数代表着液体流动过程中的沿程损失和局部损失。液压阻力系数Kq1,Kq2,Kq3,Kq4和前冲机的损失系数ξq1,ξq2,ξq3,ξq4取值的准确与否影响着液体腔Ⅲ中压强变化规律计算的准确性。n的取值影响着气体腔压强变化规律的求解,fy取值是否准确影响着游动活塞运动规律求解结果的准确性进而影响液体腔Ⅰ中压强求解的正确性。

制退机方程中的待辨识参数包括：制退机液压阻力系数Kz1,Kz2,Kz3,Kz4,制退机的液压阻力系数取值是否准确直接决定了制退机液体腔压强差解算结果的准确性,对火炮发射过程中制退机力的计算起着至关重要的作用。

待辨识的参数有16个,分别为Kq1,Kq2,Kq3,Kq4,Kz1,Kz2,Kz3,Kz4,ξq1,ξq2,ξq3,ξq4,n,fy,Ff,μ。待辨识参数的初始范围如表1。

表1 待辨识参数的初始区间

2.2 参数辨识问题数学模型

参数辨识以寻优算法为基础,寻找一组参数使得动力学模型的计算数据与试验所获得的数据的时间序列相似度的值最大,即数值仿真数据与实测数据之间的误差最小。为了与本文算法结合,将参数辨识模型做一定转换,转化为求最小值的问题。其数学模型为

(14)

式中：xd为第d个待辨识参数;f(xi)为仿真输出的第i个曲线;Di为第i个试验数据曲线;S(fi(X),Di)为第i组数据的相似度;αi为第i组数据相似度的权重系数;F为性能函数。本文需要进行相似度拟合的数据一共有两组,分别为速度和位移,因此n=2。

式(14)中相似度S综合考虑了曲线的数值相似度与形状相似度两部分,相似度S的范围为[0,1]。S=0表示两个组数据的所有特性均不相同;S=1表示两组数据的所有特性高度一致。曲线数值相似度是计算的两点间的欧氏距离,曲线形状相似度的计算依据的是界标分界法[16]。

3 改进型免疫克隆布谷鸟算法模型及流程

3.1 改进型免疫克隆布谷鸟算法模型

3.1.1 算法描述

随机产生规模为N的初始抗体种群X(0)= {X1,X2,…,XN}在d维搜索空间中进行搜索计算,记第i个抗体为Xi={x1i,x2i,…,xdi},i=1,2,…,N。当前抗体种群的亲和度为aff={aff1,aff2,…,affN},抗体浓度den={den1,den2,…,denN},激励度为sim={sim1,sim2,…,simN}。该算法通过对抗体种群按照激励度从小到大排序,根据克隆算子对每个抗体逐一进行克隆,克隆完成后进行抗体随机交叉、高频变异、精英抗体提取、疫苗接种、免疫选择、Lévy飞行策略、巢寄生行为和种群刷新,逐次迭代直至完成计算。算法描述如图3所示。

图3 算法描述

3.1.2 激励度计算

激励度是对抗体质量的评价,需要综合考虑抗体的亲和度和浓度,通常亲和度高和浓度低的算子激励度较大。

simi=a·affi-b·deni

(15)

式中：simi为第i个抗体Xi的激励度;a为亲和度系数;b为浓度系数。对于本文参数辨识问题,亲和度即为性能函数F,如式(14)。

(16)

(17)

式中：N为抗体种群规模;f(Xi,Xj)为抗体相似度;δ为相似度阈值。

3.1.3 克隆算子

(18)

根据文献[17]定义克隆规模函数。式中：Nc为克隆后的抗体种群规模;k为克隆倍数,用来决定克隆种群的规模 ,k越大克隆种群数量越多;[·]为取整函数。定义克隆后的抗体种群为Xc。

3.1.4 随机交叉、高频变异与自适应操作

对克隆抗体种群进行随机交叉有利于增强种群的多样性,为后续的变异操作提供更多的搜索中心,增强跳出局部最优的能力。高频变异则是在交叉运算得到的更优抗体的基础上再进行一遍局部随机搜索。高频变异操作的搜索范围随着迭代次数的增加而减小,从而使后期的搜索空间更小,提高收敛精度。针对交叉、变异概率为固定值,算法不易取得最佳概率值的问题,引入了张玲等的自适应算子。

(1) 随机交叉算子

(19)

(2) 高频变异算子

(20)

(21)

(22)

式中：rd1,rd2,rd3,rd4为随机数;P一般取0.5;pc为交叉概率;pm为变异概率;t为当前迭代数;T为总迭代数;r与b1为正常数。从式(22)可以看出,随着进化,t接近于T时,η(t)≈0,从而在进化后期进行精细搜索。

(3) 自适应算子

(23)

(24)

式中：Pc_max为交叉概率最大值;Pc_min为交叉概率最小值;Pm_max为变异概率最大值;Pm_min为变异概率最小值;affavg为平均亲和度。

3.1.5 精英抗体提取算子

对变异后的抗体种群Xm进行优质抗体的提取,当前种群Xm中的抗体数目为Nc,从中提取依据抗体亲和度排序后的前N个精英抗体参与后续的计算,提取操作避免劣质的冗余计算,缩短计算时间。

(25)

3.1.6 疫苗接种与免疫选择

待接种的疫苗是根据先验知识和问题背景从克隆抗体种群中提取出来的最优抗体,将其存储在记忆细胞中备用,记为V=(V1,V2,…,Vd)。疫苗接种是将待接种疫苗依据接种概率与精英抗体上部分基因进行替换。免疫选择即对比子代与父代抗体的亲和度,若抗体亲和度提升,则保留,反之舍弃。

疫苗接种如式(26)所示

(26)

3.1.7 Lévy飞行策略和巢寄生行为

引入布谷鸟搜索算法(cuckoo search,CS)的Lévy飞行策略和巢寄生行为将有利于提高疫苗接种后种群的多样性,避免陷入局部最优,同时在高质量种群基础上的二次搜索更有利于向最优解靠近。

(1) Lévy飞行策略

XLi=Xvi+αLévy(λ)·(Xvi-Xbest)

(27)

(28)

(2) 巢寄生行为

Xi=XLi+r(XLj-XLk)⊗H(pa-r)

(29)

式中：r～U(0,1)为随机缩放因子;⊗为点乘积;H(·)为Heaviside函数;pa为发现概率,通常取0.25;XLj,XLk为随机选取的互不相同的抗体。

3.1.8 抗体种群刷新与合并

抗体种群的刷新为在全局范围内随机生成N个抗体组成一个新种群Xn,从而达到大范围全局搜索的目的,防止抗体种群陷入局部最优。新生成的新种群,按照亲和度排序,取前N/2个与巢寄生行为更新后的抗体种群X中的前N/2个进行融合。

3.2 改进型免疫克隆布谷鸟算法流程

步骤1初始化,生成初始抗体种群X。

步骤2计算初始抗体种群X的激励度。

步骤3按照激励度对X抗体中进行排序,然后进行克隆操作,生成克隆抗体种群Xc,提取疫苗V。

步骤4对克隆抗体群Xc进行随机杂交和自适应变异操作,得到新抗体种群Xm。

步骤5对抗体种群Xm进行精英抗体提取操作得到新的抗体种群Xe。

步骤6对抗体群Xe进行疫苗接种操作,获得Xv,然后对其进行免疫选择。

步骤7对Xv进行Lévy飞行全局搜索更新操作生成新的种群XL,对XL进行巢寄生行为局部搜索操作生成抗体中群X。

步骤8种群刷新生成Xn,将Xn与X抗体种群按亲和度进行排序,将各自前N/2个抗体进行融合,生成最终的混合种群X。

步骤9判断是否满足停止条件,不满足执行。

IICCA算法的流程框图,如图4所示。

图4 IICCA算法的流程框图

4 IICCA性能分析与对比

为了验证所提出的IICCA的性能,将IICCA与ICSA,IGA,APSO和ICS进行对比。5个多峰标准测试函数如表2所示。各算法的仿真参数如下：IICCAPm_max=0.7,Pm_min=0.1,Pc_max=0.7,Pc_min=0.3,a=2,b=1,δ=0.3,k=0.5,pv=0.6,b1=2,r=0.5,α=1;在ICSA中,pm=0.7,δ=0.3,k=0.5,a=2,b=1,pa=0.25,α=1;在IGA中pm=0.7,pc=0.2,pv=0.6,δ=0.3,k=0.5,a=2,b=1;在APSO中c1=c2=2,wmax=0.7,wmin=0.4;在ICS中αmax=0.5,αmax=0.01,pαmax=0.5,pαmin=0.005。各算法的最大迭代步均为300,寻优维数为15维。将5种优化算法在5个标准测试函数上进行50次寻优,测试结果如表3所示,进化曲线如图5～图9所示。上述5个测试函数形态复杂,都是较为复杂优化问题,具有很好的测试性能,可以有效的验证IICCA的收敛速度和精度、全局收敛性能和多峰寻优能力。

表2 标准测试函数

表3 算法测试结果

图5 Ackley函数的动态寻优过程

图6 Griewank函数的动态寻优过程

图7 Lévy函数的动态寻优过程

图8 Rastrigin函数的动态寻优过程

图9 Schwefel函数的动态寻优过程

由表3中数据可以分析出IICCA算法对上述5种多峰寻优函数均具有较高的计算精度,且计算时间明显低于IGA,计算精度明显高于其他4种算法。相比经典ICSA,本文提出的算法计算精度得到了明显提升。虽然对于免疫克隆选择算法引入了疫苗接种、高频变异、布谷鸟算法等,但是算法的计算时间并未明显增加,表明该算法在满足计算快速性的同时提高了收敛速度和精度。由表中的标准差分析可知,IICCA算法的稳定性很好,同比其他4种算法稳定性具有明显优势。

由图5～图9可知,IICCA的全局寻优性能优于其他4种算法,且收敛速度更快。IICCA寻优时20代之内就可收敛。在图7中,对于Levy函数,虽然IICCA前期的下降速度比IGA慢,但是150代之后,IGA的收敛速度明显趋于平缓,IICCA仍然处于快速收敛状态,最终IICCA的收敛精度明显高于IGA。在图9中,对于Schwefel函数,IICCA算法的精度明显高于其他4种算法。本文算法将ICSA进行改进后与CS算法进行融合,显著提升了算法的性能,新算法IICCA明显优于原本的ICSA与CS算法,同时也优于一些其他的改进算法。

综上所述,本文所提出的IICCA算法具有更高的收敛精度,更快的收敛速度,以及更优的全局寻优能力,完全符合工程实践的精度要求。

5 基于试验数据的参数辨识验证

5.1 软后坐火炮发射试验

本文以某大口径软后坐火炮发射试验为例,设定软后坐火炮初始位置为原点,炮口方向为速度正向,采样频率为10 000 Hz。试验采集到的数据有后坐部分的位移和后坐部分的速度。测试结果曲线如图10、图11所示。测试数据1和测试数据2为同种试验条件下测得的数据,测试数据1和测试数据3为不同前冲击发位置条件下测得的数据。

图10 后坐部分速度测试曲线

图11 后坐部分位移测试曲线

5.2 参数辨识结果

将IICCA用于软后坐火炮发射过程参数辨识时,利用测试数据1为辨识目标值,测试数据3的用于辨识验证,独立进行5次参数辨识。根据式(14),参数辨识后速度曲线与位移曲线的性能函数F的平均值为0.029 8,相似度为97.02%。经过辨识后得到上述16个参数的辨识结果如表4所示,参数辨识后的后坐部分速度曲线见图12,位移曲线如图13所示。由图12和图13可知,辨识曲线与测试曲线具有较高的相似度,辨识结果可靠。

表4 辨识参数结果

图12 测试速度与辨识速度对比曲线

图13 测试位移与辨识位移对比曲线

5.3 参数辨识算法比较

为了进一步验证本文提出算法的优越性,将ICSA,IGA,ICS,APSO与IICCA分别用于软后坐火炮试验数据的参数辨识,分别独立运行10次后取均值,进化代数300代,其余参数均与前文选取一致。获得的各算法参数辨识性能函数进化曲线如图14。由图14可知,IICCA收敛速度比其他4种算法快,收敛精度也是最高的。因此本文的IICCA较于其他算法更适用于多参数辨识的问题。

图14 性能函数收敛曲线对比

6 结 论

根据牛顿动力学方程和伯努利方程建立了软后坐火炮发射过程的动力学模型,针对火炮发射过程中,未知参数多,辨识困难的问题,对免疫克隆选择算法引入自适应算子,疫苗接种策略、高频变异、随机交叉和精英提取算子,提高了原算法的收敛速度和计算精度,再与布谷鸟算法相结合,提出了一种新算法,即改进型免疫克隆布谷鸟算法。通过对IICCA算法的研究和软后坐火炮发射过程的参数辨识,获得了以下结论：

(1) IICCA算法在求解测试函数时,计算结果表示,IICCA算法寻优能力明显优于其他4种算法和单一类型的寻优算法,IICCA算法具有收敛速度快,计算精度高、全局搜索能力强的特点。测试结果还表明该算法的计算时间并没有明显的增加,因此满足计算快速性的要求。

(2) 辨识结果表明,IICCA算法在求解软后坐火炮多参数辨识问题时,收敛速度明显快于其他4种算法,收敛精度也较高。因此该算法在求解多参数辨识问题时,具有明显的优势。