基于核磁共振的土体有效孔隙比及其渗透性研究

卢伟, 冯楚桥, 董均贵, 赵芳

(1.广东省交通运输建设工程质量检测中心, 广东广州510420;2.贵州省水利水电勘测设计研究院有限公司, 贵州贵阳550002;3.贵州大学资源与环境工程学院, 贵州贵阳550025)

0 引言

土质路基可视为多孔隙介质,其孔隙水渗流作用对路基强度、回弹、整体稳定性等都具有显著影响[1]。暴雨和排水不畅情况下路基横断面上易产生水头差而引起横向渗流,导致路基土体孔隙冲刷,细颗粒流失,黏聚力降低,严重损害路基稳定性和服务功能。孔隙是土体水分渗流的通道,建立考虑水头差和孔隙结构影响的土体渗透性评价模型,对路基稳定性分析与防渗设计具有重要价值。

土体渗流一直是学术界和工程界关注的热点话题,国内外学者提出了许多评价土体渗透性的经典模型,如Terzaghi 模型[2]、Kozeny-Carman模型[3]、Poiseuille模型[4]、Darcy模型[5]等。这些模型详细地分析了与土体渗透性相关的诸多因素,能较准确地计算粗粒土渗透系数,但用于黏性土渗透系数计算仍不够准确,其原因之一是粗粒土与黏性土中的孔隙水储存形态及其迁移特性存在显著差异[6-7]。粗粒土中黏粒含量较少,小孔隙占比较低,而黏性土则以小孔隙为主。小孔隙中储存束缚水和毛细水占比较大,而大孔隙中则多为重力水[8]。重力水在自重作用下便会发生流动,毛细水需在一定压力下才发生流动,而束缚水则紧紧地吸附在小孔隙内。Zhang等[9]研究认为,束缚水的性质接近固体,它们所占据的孔隙不参与渗流作用,这部分孔隙含量常与介质渗透率成反比。党发宁等[10]也认为,束缚水所占孔隙对渗流无贡献,在土体渗透系数计算时应扣除这部分孔隙体积,以有效孔隙比修正的渗流模型更为合理。另外,Greve等[11]、Zhang等[12]认为当压力(水头)增大时,土体中参与渗流的有效孔隙体积会增多,有效孔隙占比增大,土体渗透性增强。可见,在不同水头差影响下,土体中参与渗流作用的有效孔隙体积是动态变化的。为了正确评价黏性土的渗透性,有必要探究不同水头差下土体有效孔隙及其渗透性,而当前尚未见到类似研究报道。

本文借助低场核磁共振技术,以吸力等效模拟水头差引起的渗流面应力,测试不同吸力下(不同水头差)土样的横向弛豫时间曲线(T2曲线),参考饱和-吸力联合测定方法将土体孔隙划分为有效孔和无效孔。定义有效孔隙比参数,并构建水头差与有效孔隙比间的数学模型。将水头差和有效孔隙比引入Kozeny-Carman模型,建立基于有效孔隙比的修正Kozeny-Carman模型,研究成果可为黏性土路基稳定性分析与防渗护设计提供理论和实践基础。

1 研究材料与方法

1.1 研究用土与试样制备

研究用土取自广西来宾市某路基项目现场(见图1),取土深度为地表以下1.5～3.0 m,并去除植物根系、腐殖质、碎石等。该土为棕红色强塑性黏质土,含水率高,含少量结核、有机质等。

图2 核磁共振仪Fig.2 NMR instrument

根据《公路土工试验规程》(JTG 3430―2020)相关规定进行室内试验,测定土的主要物性参数与矿物组成,本文中采用误差小于5%的3次试验数据均值作为最终结果,土的基本物性参数见表1。

表1 研究用土的基本物性参数Tab.1 Basic physical parameters of soil sample

受限于核磁共振测试管尺寸,试验中采用非标准环刀试样,试样尺寸为直径为40 mm,高度为40 mm的圆柱形土样。环刀为聚四氟乙烯材料特制而成,从而避免对核磁共振测试系统固有磁场造成干扰。综合考虑路基压实度要求与室内击实试验结果,试样干密度设置为1.8 g/cm3。制样时,先使用过2 mm筛的土制备含水率约为10.0 %的湿土,密封保存48 h使土体含水率均匀。再使用静压法制取密度差在±0.2 g/cm3的5个试样,并进行抽真空饱和。最后,测定试样在不同吸力下的核磁共振T2曲线。某级吸力下的T2曲线进行4次平行测试,取数据最接近的2条曲线计算均值绘制成最终的T2曲线。

1.2 不同水头差下的核磁共振试验

文献[13]提出用饱和-吸力联测方法测定不同吸力下的T2曲线,进而分析孔隙水形态及土体孔隙结构特征。对于饱和土体,在吸力逐渐增加过程中,土体孔隙水将逐渐排出,即不同吸力下土体可排出水量不同,也可认为参与渗流的有效孔隙体积是动态变化的。对于自由水面下的某点,其沿各个方向的水压力是相等的。采用吸力对土体孔隙水施加竖向应力,可近似的模拟孔隙水在等效水头差下的竖向受力状态。参照文献[13],并考虑路基填筑高度以及暴雨山洪极端情况对路基两侧水头差的影响,本文最高水头差取50 m,用吸力模拟不同水头差下孔隙水受到的竖向应力。对单位长度的路基,假定水密度为1 g/cm3,吸力值分别设置为0、10、20、40、80、160、320、500 kPa,其模拟的水头差分别为0、1、2、4、8、16、32、50 m。试验详细步骤如下：①按要求制取试样并充分饱和,计算试样初始含水率和初始孔隙比;②测定饱和试样的核磁共振T2曲线,该曲线视为试样吸力值为0下的T2曲线;③将试样置于压力膜仪中,施加10 kPa吸力,此时试样开始排水。待试样排出的孔隙水量不再变化(约3～5 d),称量试样计算其实时含水率,并测定此时非饱和试样的T2曲线;④将步骤③中试样重新放置于压力膜仪中,施加20 kPa吸力,待试样排水量恒定后,计算试样含水率并测定T2曲线;⑤重复上述步骤②至④,依次对试样施加40,80,…,500 kPa吸力,并测定不同吸力下的T2曲线。⑥整理不同吸力下的T2曲线,进行数据分析。

1.3 核磁共振原理

核磁共振 (nuclear magnetic resonance,NMR)是原子核由于外加磁场作用下在能级之间的共振跃迁现象,它是一种新型的快速、无损检测技术,已在医学、石油勘探、岩土工程等领域广泛应用[14-15]。在外加磁场作用下,获取质子数和质子由平衡位置发生偏转后又重新恢复平衡位置所需自旋轴弛豫时间T2。T2的大小与质子受束缚状态相关,T2曲线的幅值分布表示恢复平衡位置质子数量。核磁共振测定介质孔隙结构的原理是,通过对1H质子核磁共振测试,反映土体孔隙水的弛豫特征,分析出孔隙水的储存形态及其占比[16]。假定土体孔隙为柱状,弛豫时间与孔隙半径间的关系可由式 (1)[17]表示。

(1)

式中：T2为流体横向弛豫时间, ms;ρ2表示土体的表面弛豫强度,通常为常数,μm/ms;r为试样孔隙半径,μm;S/V为孔隙表面积与其内部流体体积之比,cm-1;Fs为孔隙形状因子 (对柱状孔,Fs=2;对球状孔,Fs=3)。 本研究使用苏州纽迈分析仪器有限公司生产的Minimr-60型低场核磁共振仪,其共振频率为23.309 MHz,磁感应强度为0.55 T,线圈直径为60 mm,磁体温度为32.0 ℃。

2 研究结果

2.1 不同水头差下的T2曲线

图3列出了水头差逐渐增加条件下,试样核磁共振T2曲线的变化规律。图3中横坐标为横向弛豫时间T2,单位为ms;纵坐标为T2对应的幅值,单位为1。由式(1)可知,T2值与土体孔隙半径成正比,幅值大小代表某一尺寸对应的孔隙相对含量。T2曲线与横坐标轴的积分面积与土样含水率成正比(见图4),水密度为1 g/cm3条件下,T2曲线积分面积与孔隙水体积成正比。

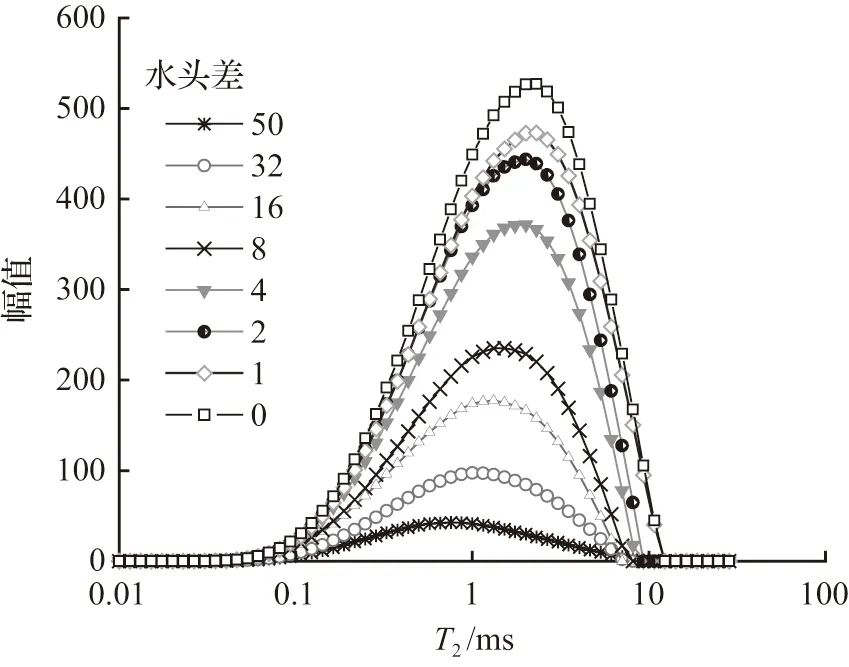
图3 不同水头差下的T2曲线Fig.3 T2 curve under various hydraulic head

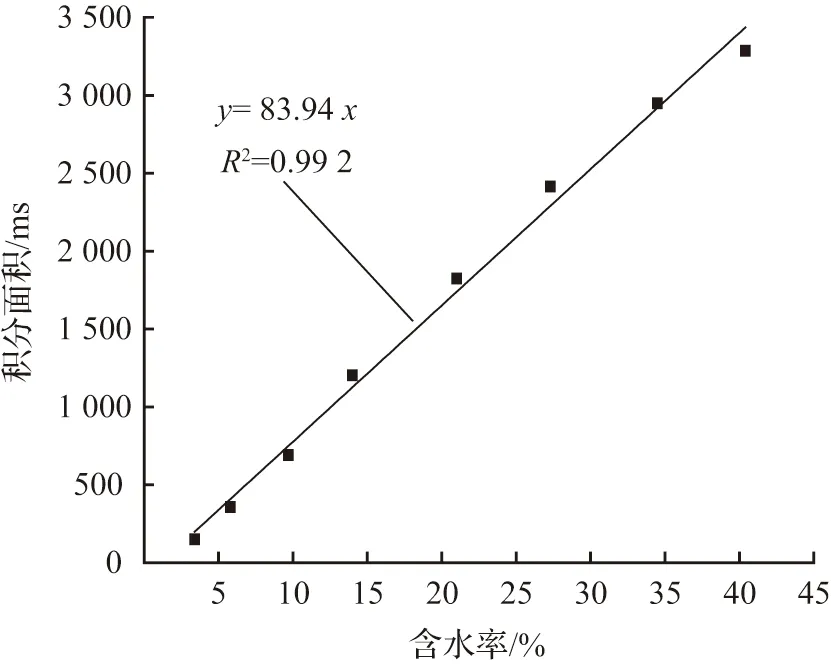
图4 T2曲线积分面积与试样含水率关系Fig.4 Relationship between T2 curve integral area and water content

不同水头差下试样的T2曲线皆为单峰形态(见图3),T2值与土体孔隙半径成正比。随着水头差增加,T2曲线峰值、曲线积分面积、曲线最大值都逐渐减小,表明当忽略孔隙收缩时,水头差越大,土体中因渗流作用排出的孔隙水量越多,且大孔隙内的水优先被排完,即水头差越大,土体中参与渗流作用的孔隙量越大。为了便于对比研究,将图3各条T2曲线的特征参数列于表2中。需要说明的是,现有研究[13,18]中关于可动水、不动水划分主要基于孔隙结构特征,即在持续增加的水头差下,孔隙水逐渐排出直至某一恒定值,将残余孔隙水定义为不动水。对于给定土体,其可动水、不动水含量为定值。而本文旨在研究渗流作用中有贡献的孔隙,不同水头差下可动水和不动水的相对含量是变化的。不动水不能作为渗流通道,其占据的孔隙对渗流而言是无效孔隙。将一定水头差下可被排出的水视为可动水,其储存的孔隙为有效孔隙。表2中,Vg表示无效孔隙体积,即在某级水头差下仍含水的孔隙(孔隙水未被排出);Vd表示有效孔隙体积,定义为水头差Δh=0时的T2曲线与某级水头差下(如Δh=1)T2曲线的积分面积之差,它表示给定水头差下被排出的部分孔隙水所占据的体积,可认为仅这部分有效孔隙参与土体渗流作用。例如,Δh=0时试样孔隙体积为3 283.78 ms,此时试样不发生渗流,有效孔隙体积为0;Δh=1时,试样无效孔隙体积为2 947.14 ms,此时参与渗流的有效孔隙体积为336.64 ms。

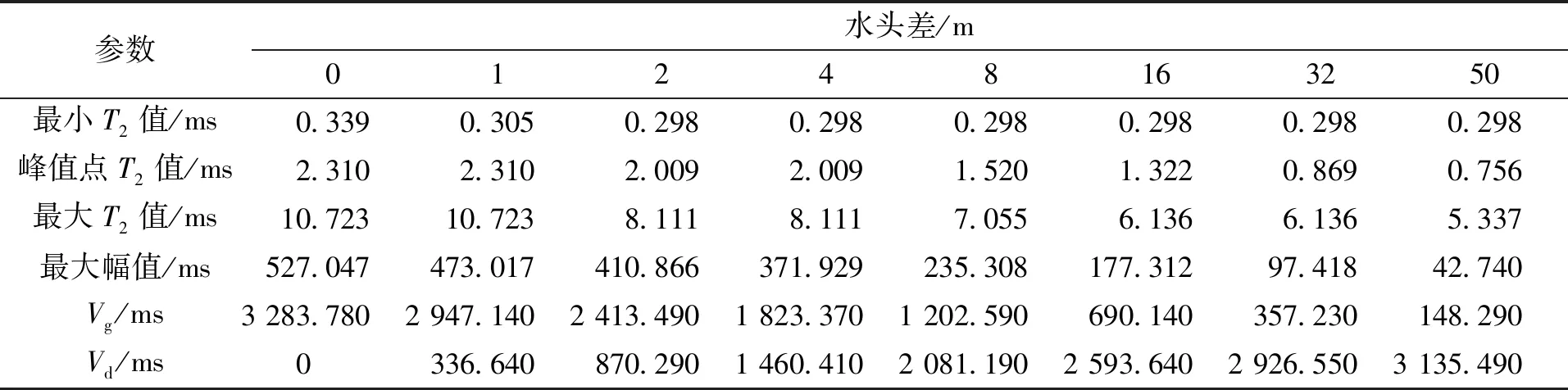
表2 不同水头差下T2曲线特征参数Tab.2 Characteristic parameters of T2 curve under different hydraulic head

据式 (1) 可知,T2与土体孔隙半径r成正比关系。表2中水头差Δh从0增加到50 m过程中,T2曲线最小值相对恒定(0.298～0.339),说明Δh增加并未明显影响试样孔径构成。最大T2值随Δh增加而逐渐减小(10.723～5.337),表明排水过程由大孔隙开始,逐渐向小孔隙发展,大孔隙中水被排出后无T2信号。T2曲线最大幅值、积分面积均与含水率相关,故Δh越大,试样含水率越小,T2曲线最大幅值和积分面积也逐渐减小。Δh从0增加到50 m,试样有效孔隙体积从0 增加到约95.5%,越来越多的孔隙参与到土体渗流作用。

2.2 有效孔隙比与水头差关系

由表2可知,并非所有孔隙都参与土体渗流过程,无效孔隙对渗流无贡献。为便于数据对比分析,定义有效孔隙比为某级水头差下有效孔隙体积与初始孔隙体积之比再乘以土体初始孔隙比,即

(2)

式中：e0为试样初始孔隙比,文中取值为0.76;ed为有效孔隙比,取值范围为[0,e0];Vdi为某水头差下的有效孔隙体积;Vd0为初始孔隙体积,即水头差为0 m时的孔隙体积。

将表1中孔隙比、表2中有效孔隙体积数据代入式(2)中,计算并绘制有效孔隙比ed与水头差Δh关系曲线(见图5)。随着Δh增加,有效孔隙比先快速增加,而后趋于稳定。在Δh从0增加到16 m时,有效孔隙比从0增加到0.6,即试样中已经有79 % 以上的孔隙参与渗流。而Δh从16 m增加到50 m阶段,ed仅从0.6增加到0.73,即约16.5%的小孔隙新参与到渗流中。可见,大孔隙在较小水头差下就可转变为有效孔隙,其储存的水受孔壁束缚作用较弱,在较小水头差下就会发生流动;而小孔隙需在较大的水头差下才转变为有效孔隙。土体的有效孔隙比存在极限值,理论上该值等于土体初始孔隙比。

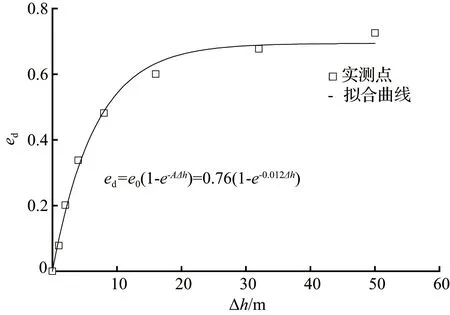
图5 水头差与有效孔隙比关系Fig.5 Relationship between hydraulic head and effective void ratio

水头差与有效孔隙比之间可用指数函数较好的拟合,即

ed=e0(1-e-AΔh),R2=0.98。

(3)

当水头差Δh=0时,ed=0;当水头差Δh=∞时,ed=e0。A为表征排水速率的参数,与土水间的固-液接触角相关,文中取0.152;Δh为水头差;R2为拟合相关系数平方。

3 讨论

3.1 水头差与T2曲线关系

在水头差作用下,孔隙水逐渐排出过程可用Young-Laplace方程[19]描述为

(4)

式中：ΔP为孔隙水气-液界面压力差;σ为孔隙水表面张力;θ为孔隙固-液接触角;r为孔隙半径。σ和θ通常为定值,ΔPi作用下试样可以排出r≥ri的孔隙内的水。

T2曲线积分面积与试样含水量相对应,水头差为0 m 时的T2曲线代表所有孔隙均充满水,水头差为1～50 m时的T2曲线表示已有部分孔隙排水(见图3)。随着水头差逐渐增加,越来越小的孔隙开始排水,T2曲线积分面积随之减小,参与到土体渗流作用中的有效孔隙体积增多(表2),土体渗透性增强。T2曲线的最大T2值随着水头差的增加而减小(见图3和表2),反映了孔隙排水是由大孔隙向小孔隙发展。当某一孔径对应的孔隙水被完全排出,其在T2曲线上的幅值即为0。需要说明的是,T2曲线幅值的大小,并不代表孔隙长短,而是孔径等于ri的大量孔隙叠加的结果,故而,曲线最大幅值对应T2值的减小(表2),说明水头差增加条件下,大孔隙中储水变少,小孔隙储水量占比增大。

T2曲线形态由土体孔隙结构决定,大多数土体T2曲线为单峰形态,部分团粒机构较发育充分的土体T2曲线呈双峰。封闭孔隙的影响导致岩石T2曲线存在多峰形态[20]。本文研究用土的T2曲线均为单峰,土体不存在明细团粒结构,孔径分布不存在断层,孔隙连通性良好。

3.2 水头差与土体渗透性

水头差增加后,土体内参与渗流的有效孔隙体积迅速增加,显著影响着土体渗透特性。Kozeny-Carman渗流模型[21]是基于孔隙结构计算土体渗透系数的经典理论,其表达式为

(5)

式中：k是渗透系数;ρw是孔隙水的密度,g/cm3;c2是与颗粒形状及水的实际流动方向有关的系数,约为0.125;s为土颗粒的比表面积,cm-1;η为自由水的动力黏滞系数,g·s·cm-2。

考虑有效孔隙比对土体渗透性影响时,将式(3)引入到式(5)中,可得到土体渗透系数与水头差的修正模型为

(6)

式中,D= (c2ρw)/(s2η)。在忽略孔隙收缩条件下,土体初始孔隙比e0可视为定值,式(6)中仅包含水头差Δh一个未知数,可为水头差影响下土体渗透系数计算提供理论参考。土体渗透系数随水头差呈指数三次方增加,可见,在高水头差下,路基土体更容易因渗流而失稳,在路基稳定性分析与防渗设计时应考虑水头差的影响。

大多数研究[10,22]认为特定土体的有效孔隙比为定值,不能体现反映土体渗透性在外荷载条件下的变化特性。本文中有效孔、无效孔的划分是基于孔隙结构与水头差共同作用的结果,兼顾土体固有特性和外荷载因素,更符合工程实际。由于土性、土水作用以及孔隙结构差异,不同土体的有效孔隙比存在差异,因此在工程运用中应结合试验数据综合评价。

3.3 算例分析

为了验证本文所得修正Kozeny-Carman模型的合理性,测定了试样在水头差分别为1、2 m时的渗透系数,并根据试样初始孔隙比和有效孔隙比分别计算渗透系数,得到渗透系数对比见表3。由表3可知,若不考虑有效孔隙比影响,直接将试样天然孔隙比代入Kozeny-Carman模型计算的渗透系数比实测值要大100倍以上,说明未经修正的Kozeny-Carman模型并不适用于黏性土。而基于有效孔隙比理论,将Kozeny-Carman模型进行修正后,修正渗透系数与实测值偏差在10倍以内,说明修正Kozeny-Carman模型更适用于黏土渗透系数计算。文献[23]的研究也得出与本文类似的结论。

表3 渗透系数对比Tab.3 Comparison of permeability coefficient

4 结论

本文借助核磁共振技术,测定水头差为0～50 m (吸力0～500 kPa)下的土体T2曲线,建立了水头差与有效孔隙比的数学关系,并讨论了水头差和有效孔隙比对土体渗透系数的影响,得到以下主要结论：

①随着水头差增加,土体T2曲线积分面积和最大T2值均逐渐减小,最小T2值几乎不变(0.298～0.339 ms)。水头差作用下,土体孔隙排水先由大孔隙开始,逐渐向小孔隙发展。

②将对土体孔隙划分为有效孔和无效孔,认为无效孔对渗流无贡献,并提出有效孔隙比定义。随着水头差增加,有效孔隙比先迅速增大,而后趋于恒定,二者可用指数函数很好的拟合。

③建立了基于有效孔隙比的修正Kozeny-Carman模型,该修正模型可为黏性土路基稳定性分析与防渗设计提供理论参考。鉴于不同土体土颗粒表面特性和孔隙结构差异,该修正模型普适性仍需进一步验证。