考虑空气对流换热的弓网电弧仿真研究

向恺, 陈建球, 荀径

(1.广西大学机械工程学院, 广西南宁530004;2.南宁学院中国-东盟综合交通国际联合重点实验室, 广西南宁530299;3.北京交通大学先进轨道交通自主运行国家重点实验室, 北京100044)

0 引言

在电气化铁路中,受电弓与接触线之间因行驶不平顺等原因易导致二者分离,出现电弧放电现象[1-2]。由于电弧放电会产生强烈高温,因此易对接触线表面产生熔池坑,也对碳滑板表面产生烧蚀[3],并且随着轨道列车运行速度的加快,弓网间接触力波动幅度增大,弓网电弧造成的故障愈发频繁。

弓网电弧是一种热-电-磁等多个物理场耦合作用的过程[4-5],目前国内外学者对弓网电弧的仿真研究较少,多集中在用磁流体模型描述电弧放电现象[6]。磁流体动力学模型是将电弧等离子体视为一种多组分流体,描述了粒子频繁碰撞下呈现麦克斯韦分布的状态,通过宏观热力学统计或化学动力学理论求取粒子组分,与N-S(Navier-Stokes)控制方程、电磁方程等联合建模,同时表征电弧宏观时空特性与微观粒子状态[7]。

王立军等[8]提出一种基于磁流体动力学的电弧开关模型,通过电流元等初值,得出真空电弧的等离子分布与电流密度分布,并且研究了开关两极间隙对电弧温度的影响,但该模型基于真空环境的假设下,未考虑空气介质对电弧的影响。郝长金等[9]在开关电弧的磁流体动力学模型基础上,考虑弓网车体振动与空气介质等因素建立了弓网电弧模型,并着重研究了电流对弓网电弧的影响。Xu等[6]在磁流体动力学模型基础上,考虑在低气压强气流下的电弧运动特性,搭建了受电弓-接触线电弧模型,得出了气流速度对弓网电弧的影响。Yang等[10]基于磁流体电弧模型,研究空气流动方向对电弧的影响,结果表明：交叉风和45°方向风对动态电弧运动形态有显著影响,对于电弧温度分布变化不大,但该模型建立在低空气流速等工况条件下,对于高速列车弓网电弧具有一定的局限性。

针对前文未考虑到高速工况下强制对流换热对弓网电弧的影响,本文中对热源项添加由空气流动引起的热源损失,并基于COMSOL的多物理场模块下,建立弓网电弧的磁流体二维仿真模型,仿真得到电弧柱区域内温度分布、接触线碳滑板表面温度分布等参数。同时,通过光谱分析法对弓网电弧温度进行测量,经过3次测量数据对比后,证实了仿真实验的可靠性,最终分析得出影响弓网电弧温度分布的因素。

1 计算方法与理论基础

1.1 磁流体动力学模型

电弧的计算基于磁流体动力学理论,将电弧等离子体视为带电流体,通过流体动力学方程得到质量、动量以及能量守恒方程,并且为描述电弧的加热效应与电场电磁力作用,对动量与能量守恒方程添加动量源项与热源项。

1.1.1 流体动力学方程

根据麦克斯韦方程组可得电弧质量守恒方程为

(1)

式中：ρ为电弧柱离子的电荷密度,C/m3;u为流场速度矢量。

动量守恒方程为

(2)

(3)

式中：u、v表示为在x、y分量方向上的运动速度,m/s;η为流体的黏性系数,kg/(m·s);p为流体压强,Pa。

Su、Sv为动量方程的动量源项,表达式分别为

(4)

(5)

式中：su、sv分别为流场内x、y分量方向上黏性动量项,N/m3;Fx、Fy分别为在分量方向上的洛伦兹力密度,N/m3;λ是热导率,W/(m·K);J为电流密度,A/m2;B为磁感应强度,T;在电弧流场中,忽略重力对电弧的影响,其外体积力等于电弧受到的洛伦兹力,其大小为JB。

能量守恒方程为

(6)

式中：T为热力学温度,K;Cp为质量热容,J/(kg·K);QW为热源项,W/m3。

其热源项QW的表达式为

(7)

式中：V为黏性耗散项;QR为电弧热辐射过程中的能量损失值;Qa为空气流动引起的能量耗散;等式右边第1项为等离子体的焓变热,第2项为黏度耗散项,第3项为焦耳热,第4项为电弧辐射热。

在能量守恒式中,热辐射损失QR项不可忽略。为了简化电弧辐射过程的计算,采用文献[11]的经验公式描述电弧热辐射模型。在该模型中将电弧柱内部分为无数个小区域,每个小区域均认为是独立的发散热单元,得到电弧的热辐射为

(8)

(9)

式中：α为玻尔兹曼常数,其值为5.670 57×10-8W/(m2·K4);k为吸收系数,与气体的压强呈线性关系;p0为标准大气压压强,其值为1.01×105Pa;T0为外界温度,K。

1.1.2 流场状态方程

为了求解以上的流体方程,还需对电磁场进行状态方程描述。

①电场方程。

根据欧姆定律以及电流守恒方程,有

div(σgardφ)=0,

(10)

J=-σgardφ,

(11)

式(10)与(11)中：σ为电导率,S/m;φ为电场电势,V。

②磁场方程。

根据安培定律以及磁感应强度与磁矢量之间的关系,有

div(gradA)=-μ0J,

(12)

B=A,

(13)

式中：μ0为真空磁导率,其标准值为4π×10-7H/m;A为磁矢量,Wb/m。

③接触线感应强度B。

前文提到接触线中的电流会在周围产生磁场,而从对电弧施加洛伦兹力,根据毕奥-萨伐定律可得[12]

(14)

式中：i为接触线中的电流,A;μ为等离子体的磁导率,H/m;h为距离接触网的垂直距离,m;eφ为单位向量。

1.2 空气对流换热修正项

与开关电弧模型的真空条件不同,弓网电弧模型的电弧柱区域处于空气介质中,因此必须考虑由气体流动引起的散热影响[13],由空气流动引起的能量耗散项Qa表达式为

Qa=Aha(T-T0),

(15)

式中：A为弓网电弧与气体接触的面积,m2;ha为空气散热系数,根据边界层理论,弓网电弧和周围气体之间的散热系数ha可以由式表示为

(16)

式中：λa为空气的热导系数,W/(m·K);δ为单元格厚度,m;Nu为努塞尔数,当空气流动较小时,可忽略其自然对流换热;当空气流动速度较大(大于5 m/s)时,此时空气将视为层流流动,其值可根据文献[14]中的强制流动散热模型计算。

Nu=CRenPr1/3,

(17)

(18)

(19)

式中：C、n均为常数,根据弓网运行工况,等离子体在电弧柱内部的流动可近似地认为是流体在管道内的流动,其常数值可以为C=0.026,n=0.8;Re为雷诺数;Pr为普朗特数。将公式(16)—(19)代入式(15)中,得到考虑强制流动散热的能量损耗项Qa为

(20)

修正后的热源项表达式为

(21)

2 仿真模型的建立

2.1 模型设置

本次仿真在COMSOL软件中建立二维对称模型,利用多物理场模块计算得出电弧柱区域内的电场与温度场参数数值。

2.1.1 形状尺寸及网格划分

接触线形状尺寸参数如图1所示。接触线横截面由2个圆相交组成,外圆半径为20 mm,内圆半径为7.55 mm。为了方便与汇流排组装,在侧面形成77°的夹角,左、右两侧最短距离为6.5 mm,最短处距离顶部3.9 mm,模型截面整体长度为13.6 mm。本次仿真为静态仿真,碳滑板截取了部分轮廓,弓网之间的初始离线距离为2 mm。图2为模型的网格分布,网格整体按照物理场控制网格划分,最小处网格精度为0.2 mm,最大处网格精度为0.6 mm。同时在电弧柱与两极接触位置添加2层0.2 mm的均匀网格,以提高接触线与弧柱之间的运算精度。

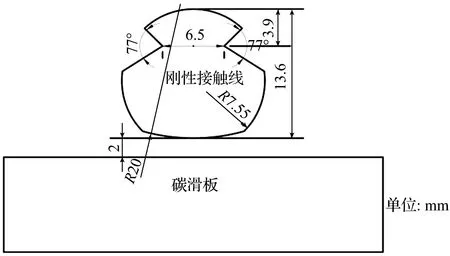
图1 接触线尺寸图Fig.1 Contact line size diagram

图2 网格分布Fig.2 Meshing diagram

2.1.2 边界条件

为了求解方程还需设立边界条件,设接触线为阳极,碳滑板接地。本模型从电流、磁场、流体传热、层流4个层面设置边界条件。

①电流边界条件。

文献[15]对电场阳极处添加高斯电流密度函数近似模拟电流密度边界源,本文中采用的电压为初始值,可将刚性接触边界视为导线,添加电压边界源,设置电压初值为750 V。

②磁场边界条件。

在求解磁场时,设置空气边界为磁绝缘体。设置磁矢位在无穷远处为0,空气边界处的磁矢位值视为0。

③流体传热边界条件。

设置流体传热边界时,默认两极与空气求解区域的初始温度为293 K,即室温条件下。为了减少计算量,将碳滑板右侧边界设置为热绝缘体。

④层流边界条件。

设置层流边界时,将外围空气边界视为强制对流,压强为一个标准大气压,流体区域考虑空气流速影响,将设空气流速恒定为0.1 m/s,方向为垂直接触线横截面方向。

2.1.3 材料物理参数

本文中选用的铜合金接触线为电弧阳极,浸铜碳滑板为电弧阴极的弓网系统作为仿真主体,其材料物理参数[16]见表1：

表1 材料物理参数Tab.1 Material physical parameters

2.2 求解过程

本次仿真的迭代步长为0.01 ms,仿真总时长为10 ms,迭代次数为1 000次;仿真初始输入为,电压750 V,弓网间隙2 mm,空气流速0.1 m/s;输出变量为电弧燃弧10 ms后的温度、电流密度以及电场强度等。弓网电弧瞬态求解过程的具体求解流程如图3所示。

图3 电弧模型的求解过程Fig.3 Process of solving the arc model

3 仿真结果与试验验证

3.1 温度场仿真结果

弓网电弧仿真结果如图4所示。图4(a)为弓网电弧在上述工况下燃弧10 ms后的整体温度分布云图。由图4(a)可知,在靠近接触线底部区域附近存在温度最大值,其值为16 439 K,但从云图上分析最大值并不在与接触线表面,其主要原因为：电弧内部温度主要来自于等离子体的焦耳热,等离子体受洛伦兹力影响压缩电弧区域,电弧产生的高温会对接触网与碳滑板造成传热,因此最高温度点不会出现与接触线直接接触位置。

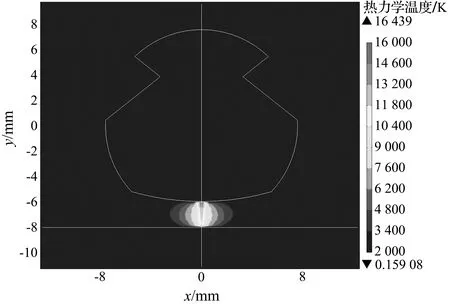
(a) 整体温度分布云图

由图4(b)可知,纵向温度分布呈现驼峰型,靠近阳极(接触线)热力学温度明显高于阴极(碳滑板),其温度最大值在靠近阳极接触线1.420 mm处取到,其值为16 439 K。取两极区域最高温度与弧柱中点处为特殊横截面,其横向温度分布如图4(c)所示。其中各截面横向温度均随横向距离的增大而降低,但8 000 K以上的高温区域分布存在差异,设各截面高温边界处的x值为高温区域半径,其值由小到大为：0.300 mm(阴极横截面)、0.478 mm(阳极横截面)、0.649 mm(中点横截面)。其中,中点截面的横向温度分布较为平缓,温差过渡平滑,可用于后续的仿真温度验证,选取距离电弧中心5.000 mm处作为待测温度点,仿真结果显示电弧热力学温度为1 963 K。

3.2 光谱测温原理

电弧的燃弧温度极高,中心区域可达到10 000 K以上,并且电弧持续时间短,因此,传统的接触式测量方法不适用于电弧温度测量[17-18]。本文中采用光谱法测量电弧温度[19]。电弧在燃弧时,弧柱中的等离子体的温度与金属粒子的辐射谱线强度有关,若能获得电弧等离子体的谱线分布,就能计算电弧等离子体的激发温度[20-21]。根据玻尔兹曼分布,谱线的发光强度可表示为

(22)

(23)

(24)

式中：ni为激发态粒子密度,mol/m3;N为总原子数;gi为上能级统计权重;Z(Te)为原子分配函数;α为玻尔兹曼常数,其值为5.670 57×10-8W/(m2·K4);εij为电子跃迁概率;h为普朗克常数,其值为6.63×10-34J·s;c为光速;Aij为从上能级跃迁到下能级的自发辐射系数;λij为跃迁发光波长;Lij为发光强度,J/s;Ω为光线立体角;V为总等离子体体积,m3;Fc为波长与系统灵敏性的修正系数。

根据式(22)-(24)可得到2条不同波长的谱线强度之比Lim为

(25)

对式(25)取对数,并代入玻尔兹曼常数,可得到

(26)

式中,D为单位换算引起的常量。

采用振子强度f代替跃迁概率Aim可进一步得到

(27)

3.3 试验结果与验证

图5为实验室自制的弓网电弧实验平台,该平台由弓网升降系统,风控系统以及测温系统组成。直流电源通过碳刷、转轮与接触线连接,同受电弓碳滑板、模拟负载一起构成电气回路,转盘另一端有电机输入转矩,可模拟弓网运行。风控系统可模拟列车行驶时的空气干扰,在本次测试中,为了防止空气流动造成的影响,将风速设置为0.1 m/s,以模拟自然对流状态。采用PG-2000型光谱仪同步采集弓网电弧的发射光谱,并通过Boltzman法测量距离弓网中心横截面5 mm处温度。

图5 弓网电弧实验平台Fig.5 Bochnet electric arc experimental platform

电源设置为直流电压750 V,负载电阻选用0.1 Ω,弓网间隙为2 mm,本次测量为静态降弓过程电弧温度测量,因此不需要开启电机。

在电弧燃弧后5 ms后拍摄到较为清晰波长范围在200～350 nm的铜原子光谱强度分布,根据光谱仪采集的光谱数据,绘制的铜原子光谱分布如图6所示。

图6 波长为200～350 nm的铜原子光谱分布Fig.6 Spectral distribution of copper atoms with wavelength 200～350 nm

选取图6中波长为222.57、282.44、296.11、306.34、333.78 nm的特征点,采用多线法计算电弧待测点温度。本实验中采用浸铜碳滑板与铜合金线作为研究主体,其中铜元素占比最大,因此还需获得铜元素的特征谱线,其完整谱线可通过查阅查阅NIST数据库获得,铜原子特征谱线参数见表2。

对表格最后两列数据用线性拟合,得到第一次电弧等离子温度拟合曲线如图7所示。由图7可计算得出拟合曲线斜率为-2.551,代入式(27)可得到距离弧柱中心5 mm处的热力学温度为1 976 K,试验所采集的特征谱线是电压在750 V工况下距电弧中心横截面5 mm处燃弧10ms时电弧外围的辐射光谱。为了防止试验的偶然性,重复上述过程,得到3次电弧测量热力学温度分别为1 976、1 966、1 983 K。

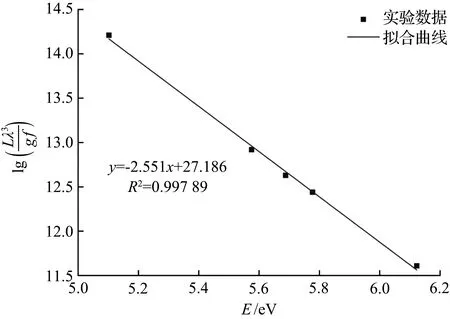
图7 第一次电弧等离子温度拟合曲线Fig.7 Temperature fitting curve of the first arc plasma

根据仿真结果,电弧柱中点截面离电弧中心线5 mm处时的热力学温度为1 963 K,对比实验所测得的3组数据,略有差异,此外还需考虑仿真中所作的假设以及试验误差,因此认为本次仿真结果基本可靠。

4 不同影响因素下仿真结果分析

4.1 电压对温度分布的影响

为了研究输入电压对弓网电弧的影响,保持其他参数不变,将电源电压从600 V增加至750 V,得到不同电压下弧柱温度分布如图8所示。通过对比分析可以得出,电弧柱内部最大温度随电压的升高而逐步上升,并且高温区域不断由阳极向阴极扩散。

(a) 600 V电弧温度分布

弧柱区域温度分布随电压变化曲线图如图9所示。由图9(a)可知,随着电压提升,阳极最高温度变化不大,在局部放大图中可看出,随着电压的增大,弧柱区域内最高温度点向弧柱中心微动,即阳极区域向电弧柱中心靠拢,但其变化趋势并不明显;与阳极区域变化相反,阴极区域向碳滑板方向微动。这样的微动增大了从阳极到阴极传热,导致碳滑板表面温度进一步升高。

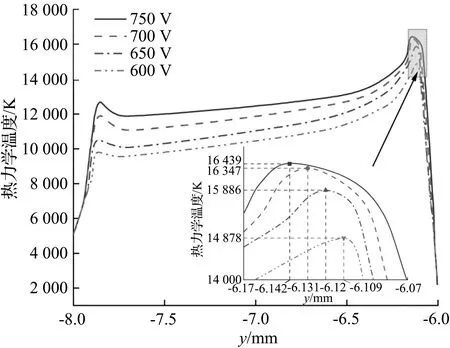
(a) 纵向温度分布

电弧柱内部温度最高点出现在阳极附近,因此还需详细研究阳极区域的横向温度分布随电压变化趋势。由图9(a)的局部放大图中可获得600～750 V电压条件下,纵向最高温度点出现的截面y坐标信息,依次取y600=-6.109 mm,y650=-6.12 mm,y700=-6.131 mm,y750=-6.142 mm。根据得到的截面坐标画出阳极最高温度点处的横向温度分布与电压变化趋势图[见图9(b)],随着电压从600 V增大至750 V,热力学温度为12 000 K以上的高温区域开始横向扩散,从0.158 mm进一步扩大至0.322 mm。

4.2 空气流动速度对温度的影响

为了研究流动速度对电弧温度的影响,将其空气流动速度分别设置为0.1、20.0、50.0 m/s,保持其他参数不变,得到电弧柱区域内温度分布云图如图10所示。由图10可知,电弧区域内最高温度随空气流动速度的提升而迅速降低,其原因主要集中在两方面：一方面,较高的空气流动速度可以将热量迅速分散至周围空气中,避免形成热量集中区域;另一方面,高速气流将一部分等离子弥散,减少电弧长度,进一步降低电弧柱区域的温度。

(a) 0.1 m/s时温度分布

4.3 导热率对材料表面温度的影响

为了研究碳滑板和接触网温度分布情况,对结果进行后处理,隐藏弧柱区域显示两极内部温度,其接触网与碳滑板温度如图11所示。其中接触网表面热力学温度最高可达713 K,温度由表面向内迅速递减,其等温线近似同心半圆分布;碳滑板的表面热力学温度最高达4 873 K,远高于接触网表面温度,其原因主要是碳滑板热导率低,热量经电弧传递到碳滑板表面,不能及时换热,累积大量热量在表面。当热力学温度上升至4 000 K时,电弧会对碳滑板表面形成熔池坑,造成熔池磨损。

图11 碳滑板与接触线表面温度分布Fig.11 Carbon slide and catenary surface temperature distribution

为了研究热导率对碳滑板表面温度的影响,控制碳滑板其他物性参数不变,分别取热导率λ为8、20、50 W/(m·K)时,其接触线内部温度分布如图12所示。由图12可知,当滑板材料热导率从8 W/(m·K)提高到50 W/(m·K)时,最高热力学温度从4 873 K下降到了2 413 K,同时8 000 K以上高温区域半径也由1.214 mm减小至0.590 mm,说明提高滑板材料的热导率可以有效地降低弓网电弧对滑板的热侵蚀程度,从而延长滑板的使用寿命,因此,在选择滑板材料时,应该优先考虑其热导率等相关性能指标,以确保其能够承受高温环境下的使用。

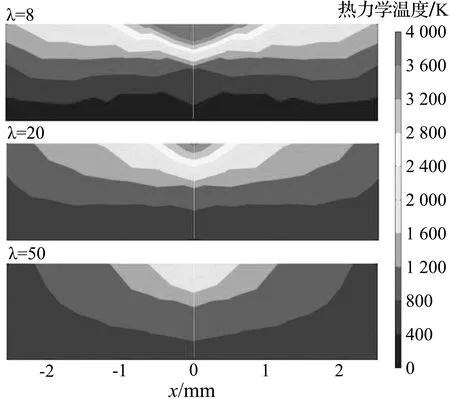
(a) 温度分布云图

5 结论

考虑强制对流换热对弓网电弧的能量耗散,对传统的磁体动力学理论进行改良,并对弓网静态离线工况进行模拟仿真,基于COMSOL软件多物理模块构建了考虑空气对流换热的磁流体仿真模型,并对仿真模型进行求解。同时通过多次电弧烧蚀实验进行验证,得出以下结论：

①电弧区域内温度纵向分布上呈现驼峰状,在两极区域均存在局部最大值,但温度最高点出现在接触线附近,并不与接触线表面直接接触;电弧区域内最大温度随着电压的增大而升高,并随电压的增大高温区域不断向阴极扩散。

②高速工况下,较高的空气流动速度可以加快电弧的散热过程,并将热量迅速分散至空气中。

③碳滑板的表面温度远高于接触线的,这是由碳滑板材料的热导率低所致,提高滑板材料的热导率可以有效降低弓网电弧对滑板的热侵蚀。