ε-动态三角采样和过渡递归回溯的RRT算法

马智焕, 胡立坤*, 陶兴华, 刘月洋, 胡正南

(1.广西大学电气工程学院, 广西南宁530004;2.南宁学院智能制造学院, 广西南宁530299)

0 引言

近年来,芯片制造技术、自动化控制技术的日臻成熟和人工智能概念的兴起,机器人的功能越来越强大,使用场景也愈加多元化,同时路径规划是机器人领域内至关重要的研究方向之一。路径规划的需求是在明确了始发地和目标位置的情况下,同时满足路径长度短、规划效率高等条件,并且搜索到与障碍物无碰撞的可行解。

常用的规划算法包括Dijkstra算法[1]、A*算法[2]、人工势场算法(artificial potential field, APF)[3]、遗传算法[4]、人工鱼群算法[5]、蚁群算法[6]、概率路线图算法[7]和快速搜索随机树(rapidly exploring random trees, RRT)算法等。其中Dijkstra算法的主要特点是由中心向四周搜索,直到扩展到终点位置为止,由于算法遍历节点多,因此容易消耗大量的时间。A*算法采用启发式的搜索,提高了全局的搜索效率,却难以满足路径最优的要求;APF算法可以获取平滑安全的路径,但是容易陷入局部最优的困境。遗传算法可以有效的搜索整个地图环境,但是实时性较差。人工鱼群算法种群数与路径质量成反比。蚁群算法虽然可以找到最优路径,但是收敛速度慢,容易发生死锁现象。概率路线图算法路径的好坏取决于空间事先设置的采样点,当采样数量不多或者分布不均匀时,很难找到路径。

文献[8]提出了基于采样的RRT算法,因为其结构简单、路径搜索效率高、拥有完整的概率完备性等特点,所以被运用在各类路径规划场景中,但是,RRT算法没有考虑路径节点的代价,导致生成的路径通常是曲折的,无法保证路径最优。RRT*算法[9]为新点在一定范围之中寻找最佳的父节点,同时将此范围内的路径点与新点重新连接,从而使得算法在采样点数量接近无穷大时可以找到最佳路径,但无法在短时间内找到最优解。Informed-RRT*[10]通过将采样点的生成范围削减到一个超椭球状态子集内来提升算法求解路径的效率,但在狭窄通道、迷宫等复杂环境中通过性较差。谭建豪等[11]将启发式思想运用到随机采样过程中,利用节点删除策略对每一个路径节点赋予相应的权重,使得算法可以保留权重更大的路径节点,提高了算法的寻路性能。文献[12]通过改变树的生长策略,利用三角不等式原理减少了路径的长度,同时在选择最佳父节点时考虑相邻节点的父节点,从而提出了收敛速度更快的Quick-RRT*算法。文献[13]提出一种基于三角不等式改变树中已存在节点连接方式,并利用转角约束增强路径的平滑度的RRT-Connect算法,在缩短寻找路径时间的同时,还通过重新选择祖节点减少路径长度。虽然RRT-Connect显示出良好的搜索环境的能力,但与RRT算法相似,其路径质量并不稳定,并且不能保证最佳。栾添添等[14]将地图划分四级采样区域,并利用概率目标偏置改变随机点的生成方向,同时设置安全距离且利用转角限制和B样条曲线拟合平滑路径。Liao等[15]提出了F-RRT*算法,通过创造一个新节点使得路径质量变得更优。陈侠等[16]利用人工势场算法削弱了RRT算法采样时的随机性,障碍物产生斥力,而终点产生引力,二者结合为随机点提供扩展方向;但是由于人工势场算法计算量较大,而且容易陷入局部陷阱,因此可能使得采样点陷入局部最优。荆泽成等[17]在RRT算法中加入目标偏置来加速算法搜索速度,但是对于复杂的环境目标偏置反而有可能限制树的生长。

基于对传统RRT采样过程的分析,研究发现随机采样效率低,ε-DT-RRT利用ε-动态三角采样区域划分采样空间,通过限制采样区域减少无效节点的数量和在无价值区域的重复采样。除此之外,通过对RRT算法结果的观察,虽然采样点是在整个地图空间随机生成的;但是很难生成最优路径上的最佳节点,因此采用创造过渡节点的方法解决了此问题。在此基础上,通过递归回溯祖节点进一步去除路径中冗余点,缩短路径长度。

1 传统RRT算法

RRT算法把已知的初始状态起点选取为随机树的源节点,在定义的地图中随机产生一个采样点,根据采样点生成一个新的子节点,不断重复此过程直至子节点到达终点时扩展终止。最后采取不断寻找节点的父节点的方式即可寻找到一条完整路径。基础RRT算法主要步骤如下：

步骤1：初始化空间信息,生成随机树T。

步骤2：在空间中均匀采样生成Xran,并搜索最近点Xnea。

步骤3：利用最近点和随机点,依据公式(1)合成Xnew。

步骤4：如果Xnew可以直接加入树中进行步骤5,反之返回步骤2。

步骤5：循环执行以上步骤,直到找到完整路径。

(1)

从以上步骤可以看出,RRT算法结构简单,但是也面临以下问题：首先,随机点是在整个地图空间上随机均匀选取的,地图环境越大,随机采样点的选择性越多,生成无用路径点的数量与概率也随之增多,消耗了大量的算法时间;其次,当Xnew与Xnea之间是直接连接,并没有经过优化,导致算法生成的路径曲折;最后,Xnew与Xnea之间存在障碍物时,算法会舍弃Xnew,而二者之间往往会有最优路径点,可能导致算法不能寻找到最优路径。

2 ε-DTSR-RRT算法设计

2.1 ε-动态三角采样区域

传统RRT算法中,因为在整个地图中随机采样生成Xran,所以会产生大量无用的采样点。针对此类问题,提出动态三角采样区域的改进措施。首先,在生成Xran前,在树中寻找距离目标点最近的节点1,根据新点1的坐标将采样区域分为已探索区域和未探索区域。已探索区域为地图中小于新点1坐标的区域,其余区域则记为未探索区域。其次,在未探索区域生成节点2,由于节点1和节点2是动态变化的,故节点1、节点2和终点构成的动态三角采样区域,如图1所示。最后,引入强化学习中ε-greedy动作选择策略,随机生成一个0～1的数记为rand,当rand小于ε(小于1的正数)时,从整个地图空间中随机生成采样点;反之,则在三角区域中随机生成采用点,如公式(2)所示。

图1 动态三角采样区域Fig.1 Dynamic triangular sampling region

(2)

2.2 创建过渡节点

针对RRT算法中,当Xnea和Xnew之间存在障碍物时,便会放弃Xnew,重新生成采样点的问题,如图2(a)所示,提出了创造过渡节点的方法。而在这种情况下,Xnew往往处于未探索区域中,为了加快对地图空间的搜索,需要联通最近点和新点,同时将新点添加到路径中。以Xnea和Xnew为对角顶点构造矩形[18]。在矩形另外两端点中任选一个处于可行区域中的点作为临时过渡节点Xt,并利用二分法优化调整Xt的位置,如图 2(b)所示。当优化完成时,进一步利用三角不等式递归回溯Xt的无碰撞祖节点Xanc,并将Xanc作为Xt的父节点、Xt作为Xnew的父节点插入树中,最终路径如图2(c)所示。由图2可知,构建的过渡节点Xt既保留了原算法中被舍弃的Xnew,又增加了算法获取最佳路径节点的机会,并联通了新的探索区域。

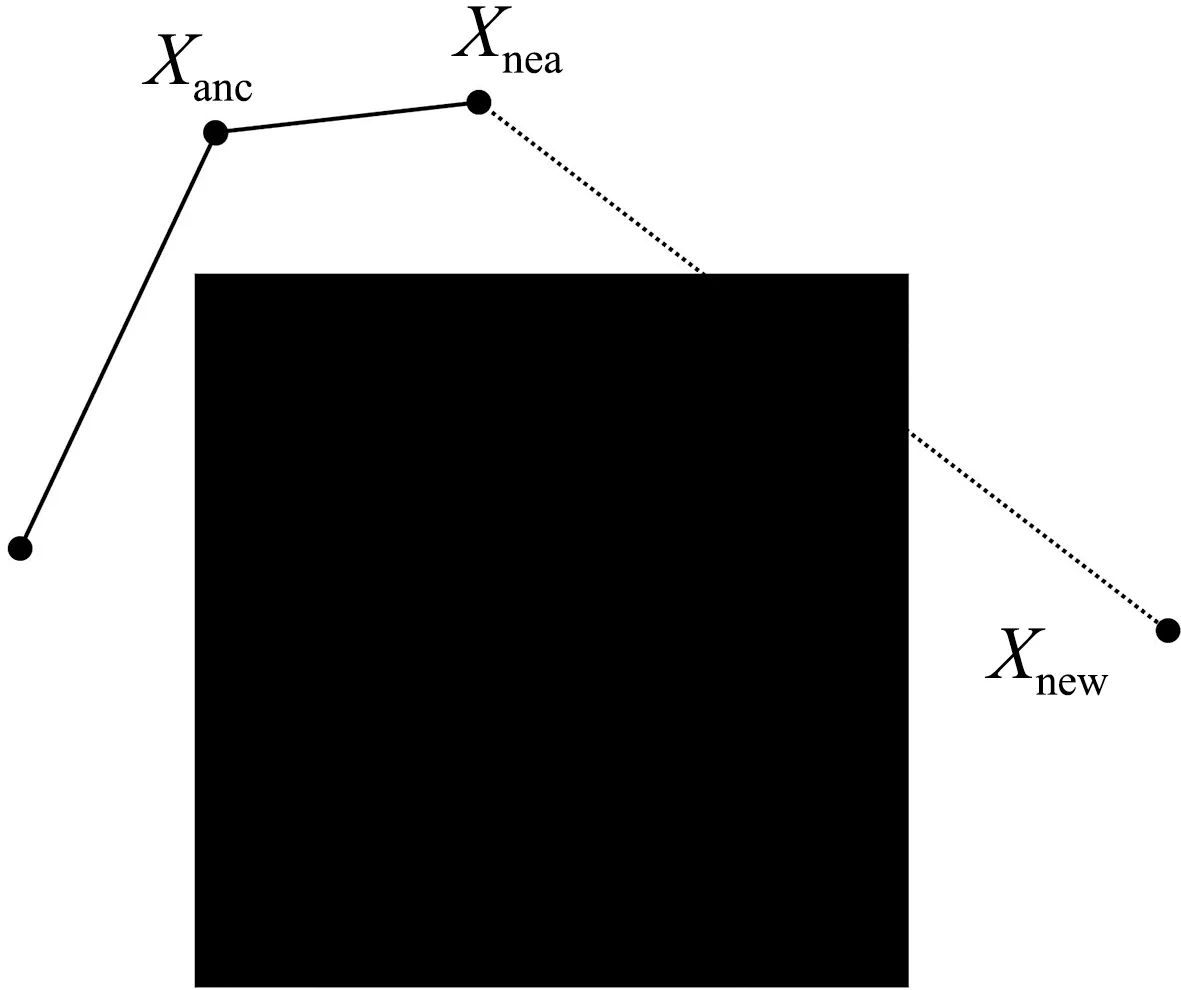
(a) 生成Xnew

2.3 递归回溯祖节点

针对RRT算法中顶点利用率低、局部最小值等情况,提出了递归回溯祖节点的方法优化路径。在Xnew作为可行路径点被添加树中之前,对最近点进行祖节点溯源。通过循环溯源操作直至择出可以与Xnew直接连接的路径点记作Xanc,将其父节点记作Xp,如图3(a)所示。由于新点和Xp之间存在障碍物,不可直接加入路径,利用Xanc,Xnew和Xp建立一个连通路径的过渡节点Xt。首先,在Xanc与新点之间搭建临时点;其次,在临时点和Xp之间生成Xt,如图3(b)所示。在此基础上,为了进一步删除拐点数量和削减路径代价,继续从树中搜集Xt可以直接连接的路径点Xtp,并加入树中。由图3(c)所示,经过递归回溯祖节点之后的路径质量明显优于初始路径。

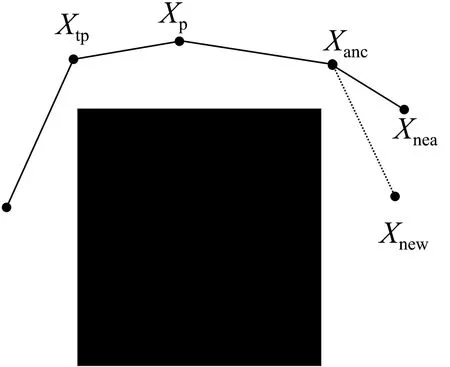
(a) 回溯祖节点

2.4 改进连接终点判别方式

传统RRT算法找到路径的标准是Xnew与终点的距离小于阈值条件即可,其局限在于不能保证新点是一直沿着终点方向拓展的,并且阈值大小也不好确定,可能会在重复的地点来回搜索,导致路径出现震荡。综合起点与终点的长度并乘以系数,记作THR。如果新点与终点的距离小于THR,启动终点直连环节,若能直接连接,说明算法已经找到路径。相对于在地图中盲目拓展的时间而言,直接连接环节消耗的时间可以忽略。

2.5 ε-DTSR-RRT算法实现

ε-DT-RRT算法具体步骤如下：

步骤1：初始化地图,设置起始点、目标点、步长等参数。

步骤2：动态三角采样区域中生成随机点Xran,在已知树中找到Xnea,并生成新点Xnew。

步骤3：判断Xnea和Xnew之间是否有障碍物。如果有跳至步骤7,否则进行步骤4。

步骤4：寻找Xnea祖节点中与Xnew没有碰撞的节点Xanc、Xanc父节点Xp。

步骤5：基于Xp和Xnew之间创造过渡节点Xt,利用二分法优化Xt。

步骤6：寻找Xp祖节点中可以直接与Xt相连的路径点Xtp,将相关节点插入树中。

步骤7：如果可以建立过渡节点Xt进行下一步,不能跳至步骤2。

步骤8：利用二分法在障碍物边缘生成Xt,并在树中寻找可以直接与Xt相连的路径点,并插入树中。

步骤9：判断Xnew与目标点之间的距离是否大于设置阈值,若大于则返回步骤2,否则,结束程序并输出路径。

3 仿真与验证

为了验证ε-DT-RRT算法路径规划效果,利用MATLAB软件仿真对比原算法和RRT类相关算法中所得路径的指标。算法的运行环境配置为笔记本电脑,操作系统版本为Windows 10 64位;CPU为i5;主频为2.5 GHz。RRT算法得到的路径都存在或多或少的差异,这是因为其具有很强的不确定性。为了减少算法的不确定性带来的实验误差,在不同的空间中运行RRT、Bias-RRT、RRT*、ε-DT-RRT算法各50次,整理实验结果对比分析。

3.1 地图1的仿真验证

地图1设定为的狭窄环境地图(180×180),用于验证算法狭窄环境下的路径指标。设置左上角为坐标原点,起始点坐标为[10,10],目标点坐标为[180,180]。选取RRT、Bias-RRT、RRT*、ε-DT-RRT算法最优路径规划结果如图4所示。虚线为迭代过程,实线段为最终路径。为了更直观地对比,将50次实验所得4种算法数据列于表1。

表1 地图1的4种算法数据对比Tab.1 Four algorithm data comparison in Map 1

(a) RRT算法

从表1可以得到,ε-DT-RRT算法在狭窄通道中的采样次数相较于RRT算法、Bias-RRT算法分别由原来的1 062.82、1 735.06缩减到225.80,分别减少了78.75%、86.99%。路径长度参数虽然与RRT*算法相差不大,但是在时间消耗和拐点数量方面各自减少了96.23%和58.00%。可以看出在地图1环境下,改进算法性能均优于对比算法。

结合表1数据和路径规划结果,改进算法在快速寻找到最优路径有一定的优势,这是因为所提算法使用了ε-动态三角采样区域一方面限制了采样点的随机性,另一方面指出了最优路径点可能存在范围,减少了生成低价值节点的时间,进而提升了算法的效率。

3.2 地图2的仿真验证

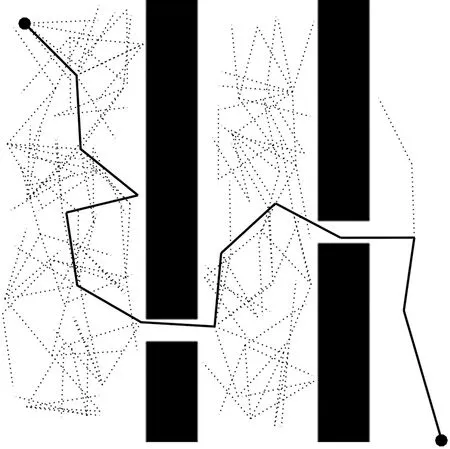
地图2设置为局部陷阱环境(500×500),用于验证算法跳出局部陷阱环境的能力。设置左上角为坐标原点,起始点坐标为[10,10],目标点坐标为[500,500]。选取RRT、Bias-RRT、RRT*、ε-DT-RRT算法最优路径规划结果如图5所示。虚线为迭代过程,实线段为最终路径。为了更直观地对比,将50次实验所得4种算法数据于表2。

表2 地图2的4种算法数据对比Tab.2 Four algorithm data comparison in Map 2

从表2可以看出,ε-DT-RRT算法采取动态三角区域采样的方式加快了算法的寻路速度,原算法需要3.14 s才能找到路径,而相对较快的Bias-RRT也需要2.09 s,但改进算法仅需要1.76 s,分别提升了43.95%和15.89%。同时从迭代次数中也可以观察到ε-DT-RRT算法的有效性,相较对比算法分别减少了51.21%、66.21%、60.46%,而迭代次数越少,也说明算法效率越高。

地图2的作用是验证算法逃离陷阱的能力,由图5可以看出,RRT算法、Bias-RRT算法、RRT*算法在面对地图左上角半包围型障碍物时均有不同程度地陷入其中,导致生成大量的冗余节点,消耗了算法的大量时间,而改进算法利用动态区域采样迅速逃离局部陷阱,提升了算法的效率。从图5(d)中,可以看出改进算法所得路径长度短,这是由于在随机树扩展的过程中和递归回溯祖节点生成了过渡节点,而过渡节点则有极大的概率是最优路径上的节点。

3.3 地图3的仿真验证

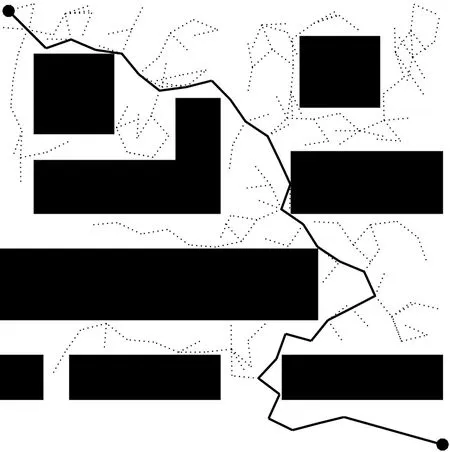
将地图3设定为复杂环境地图(500×500),除地图环境设置以外,其余设置同上,4种算法路径对比如图6所示。虚线为迭代过程,实线段为最终路径,将50次实验所得4种算法数据列于表3。

表3 地图3的4种算法数据对比Tab.3 Four algorithm data comparison in Map 3

(a) RRT算法

从表3可知,ε-DT-RRT算法有效地剔除了冗余节点,相较于RRT算法、Bias-RRT算法及RRT*算法分别减少了72.29%、71.01%、65.70%,同时迭代次数也收缩了64.91%、77.48%、70.62%。最佳路径代价和平均路径代价分别为841.96、888.84 m,比原算法减少了16.76%和26.27%。搜索时间也由原来的2.19 s缩短到1.35 s,减少了38.36%。

地图3为复杂环境,其中设计了狭窄通道,局部陷阱等复杂地形。由表3可知,改进算法在复杂地形环境平均仅用了440次迭代就达到了远低于具有最优性的RRT*算法1 500次迭代的效果。这是因为,ε-动态三角采样区域结合将地图划分为最优区域和次优区域,最优区域中的点往往是最优节点,可以快速通过狭窄通道和逃离局部陷阱。从图6中算法的路径对比可以看出,改进算法通过在障碍物附近创造过渡节点,通过连接过渡节点避开障碍物,使得路径更短;进一步利用递归回溯祖节点的方式,去除路径上的冗余节点,减少了路径上的转折点,从而得到平直的路径,进一步减少移动机器人转弯时的能耗。

通过在不同地图上测试分析,ε-DT-RRT算法在所选取的路径指标中均优于基础RRT、Bias-RRT、和RRT*。在相同的地图环境中,改进算法能够生成更为简洁的规划轨迹,路径搜索时间更短,路径迭代效率更高,路径规划效果更为显著。

3.4 算法的概率完备性

诸多学者已经论证过RRT算法是概率完备的,即在任意存在路径的地图中,只要RRT算法迭代的次数足够多,Xnew总会进入到终点目标范围内,即找到一条无碰撞的路径。所提算法在传统RRT算法上改进,提出ε-动态三角采样区域来限制采样点的区域,利用过渡节点创造无障碍路径,采用递归回溯的方式消除路径的转折点,使得算法可以更快地找到路径。改进算法以ε的概率探索未知的区域,1-ε的概率探索最优区域,在采样点足够多的情况下,采样点可以遍历整个地图,故ε-DTSR-RRT算法依旧是概率完备的。

4 结论

为了解决传统RRT在路径规划存在的问题,提出了一种ε-DT-RRT算法,通过理论分析和实验仿真,得出以下结论：

①通过ε-动态三角区域划分地图采样空间,限制随机采样点的生成位置,从而减少次优区域的搜索次数和无效节点的数量,提升了采样效率,同时兼顾了采样点的全局性和最优性,加快了算法的收敛速度。

②针对传统RRT算法在Xnea和Xnew之间存在障碍物时舍弃Xnew的问题,提出了创造过渡节点的方法。过渡节点通常是最优路径上的节点,能够靠近障碍物并保持安全的距离,提升了获取最优路径节点的概率,有效地缩短了路径长度。

③运用递归回溯祖节点的方法,通过连接新点和祖节点达到缩短路径长度和减少冗余点的效果。在此基础上,为无碰撞祖节点的父节点和新点之间创造过渡节点,能够进一步改善路径质量。

从上述的仿真实验结果来看,在3种不同的地图中,相比于RRT算法、Bias-RRT算法及RRT*算法,改进算法减少了路径中节点的数量,优化了路径的长度,得到了更短的路径;同时减少了迭代次数,缩短搜索的时间。通过上述的数据对比可以看出,ε-DT-RRT算法极大地提高了算法搜索路径的速度、质量和效率,证明了其在路径规划方面具有很强的优越性。