动态场景下结合深度学习和平移约束的SLAM算法

李桢哲, 黎展荣, 姜超

(广西大学计算机与电子信息学院, 广西南宁530004)

0 引言

同步定位与地图构建(simultaneous localization and mapping, SLAM)是移动载体,如机器人等在自身位置不确定的条件下,在完全未知环境中创建地图,同时利用地图进行自主定位和导航[1-2]。SLAM系统可以使用多种传感器,如相机、激光雷达等。其中,相机更加经济,同时提供了丰富的视觉和环境信息,具有巨大的发展潜力[3]。SLAM系统可以分为特征法[4-7]和直接法[8-10]。在特征法中,ORB-SLAM2[11]是比较鲁棒的视觉SLAM系统;但在实际应用中,含有运动物体的场景是比较常见的,因此对传统视觉SLAM系统带来了一些挑战。纯视觉的SLAM系统,需要提取图像上的特征点,并依赖于匹配好的特征点对进行位姿估计。动态环境中,系统同样会在运动物体上提取特征点并产生匹配点,由于运动物体不满足多视图几何,因此这样的匹配点反而会干扰位姿的估计,当环境中的运动物体过多时,甚至导致建图失败。为了使视觉SLAM系统在动态环境下能够正常工作,通常的做法是预先剔除运动物体,以避免系统使用其所在位置的特征点。

为了解决上述问题,许多科研人员做了大量的研究工作,得益于深度学习的快速发展,基于此的解决方案不断被提出。Yu等[12]提出了基于RGB-D的DS-SLAM系统,结合语义分割和移动一致性检测方法,以过滤动态物体,但实验过程中过滤的对象仅仅是人。Bescos等[13]提出了DynaSLAM系统,在使用RGB-D相机的情况下,结合了实例分割网络和多视图几何法检测运动对象。在单、双目相机的情况下使用实例分割网络Mask R-CNN[14]分割所有潜在运动对象(如车辆和行人),使SLAM系统不在这些物体上提取特征点,但在这种情况下,可能丢失过多的静态特征点,导致定位失败。张金凤等[15]使用YOLOv3目标检测算法提取潜在运动对象,并使用非潜在运动区域提取特征点,同样存在特征点过少的风险。徐少杰等[16]提出用目标检测网络 YOLOv4提取动态特征点,并利用语义分割网络重建三维语义地图。Zhang等[17]提出用目标检测网络YOLOv5检测动态物体,并利用光流方法剔除检测到的动态点。Xiao等[18]提出了基于单目相机的Dynamic-SLAM系统,该系统使用SSD检测潜在运动物体,针对检测召回率低的问题,提出了基于相邻帧速度不变的漏检补偿算法,大大提高了召回率。为了提取出真正运动的物体,通过计算静态点的平均位移,然后根据平均位移判断潜在动态点是否在移动。Zhang等[19]采用目标检测定位动态区域,通过深度图进行K均值聚类算法提取移动区域。

针对SLAM系统在摄像机位姿估计中平移占主要部分的环境中,提出一种在动态环境下,基于RGB单目相机的结合深度学习和前向平移约束算法SLAM系统。

1 ORB-SLAM2系统流程与框架

ORB-SLAM2系统包含跟踪线程、局部建图线程和回环检测线程。跟踪线程通过每一帧寻找特征点与局部地图匹配并通过最小化重投影误差进行相机位姿估计,实现相机定位和跟踪的线程;局部建图线程管理局部地图并优化,实现局部光束法平差(bundle adjustment, BA);回环检测线程进行检测回环并通过位姿图优化消除累积漂移误差。本文将改进的YOLOv5目标检测算法以及运动场提取算法作为动态物体剔除线程加入到ORB-SLAM2系统中。改进的ORB-SLAM2系统框架如图1所示。深色部分表示所做工作,输入RGB图像序列,然后逐帧通过YOLOv5进行目标检测,框定出有可能运动的区域。同时,相邻2帧图像通过运动场提取模块,得到运动场信息,其为0、1的二值图片,“0”代表该点为动态,“1”代表该点为静态。运动场信息结合YOLOv5的框定结果,确定真实运动区域,然后跟踪线程的特征提取模块和特征点,通过判断结果决定是否保留提取的特征点,最后经过前向平移约束进一步剔除异常匹配点,从而提升估计的精度。

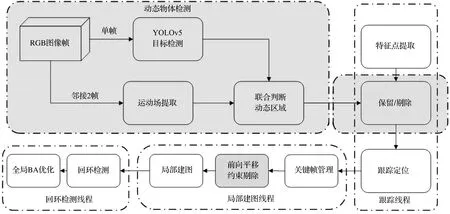
图1 改进的ORB-SLAM2系统框架Fig.1 Improved ORB-SLAM2 system framework

2 动态物体检测算法

2.1 基于深度学习的运动场提取算法

网络结构参照Depth and Motion Net[20],其网络结构如图2所示。该网络包含2个卷积神经网络,分别为Depth、Motion网络。其中Depth网络采用编码器-解码器架构,基于ResNet18网络模型,对深度使用softplus激活函数,在网络中的每个线性整流函数(rectified tinear unit, ReLU)激活之前应用随机层归一化。Depth网络主要功能是从单个图像预测深度图,为预测运动场提供信息。Motion网络基于U-Net架构,接收一对连续帧及其对应的深度图,输出一个六维向量,表示2帧之间每个像素相对背景运动的向量,分别为三维的旋转向量和三维的平移向量,同时输出像素级别的残差平移场,每个像素代表在背景运动向量的基础上还需要的平移量。训练网络使用的是重构图像损失,即第一帧图像F1通过深度图、背景运动位姿、残差平移场重构第二帧图像F2,最后采用光度一致性损失度量重构图像与第二帧图像的差异来进行训练。

图2 Depth and Motion网络结构Fig.2 Depth and Motion network structure

网络训练完成后,运动场信息可以从残差平移场中提取出来。残差平移场是一个RBG图像,因为物体不是移动的,就是静止的,所以还需转换为二值图片,其像素取值ρ为

(1)

式中：m为图像像素平均值;a为阈值系数;Ii∈R为平移场像素值。因为动态物体在整个拍摄画面中占小部分,大部分像素属于静态像素,所以当像素值偏离平均值超过阈值时,则被判定为动态像素,不同a值的比较效果如图3所示。图3(a)为原图,图3(b)为对应的残差平移场,过小的a值将导致大量像素点被误判为动态像素,图3(c)、(d)展示了合适的a值的效果;而过大的a值将导致运动区域划分残缺严重,如图3(e)、(f)。

(a) 原图

2.2 改进的YOLOv5算法

为了提高YOLOv5对小目标的检测精度,做出了如下改进：

引入Squeeze-and-Excitation(SE)模块[21]。在传统的卷积网络中,默认每个特征层的每个通道都同等重要,即它们的权重都是相等的,但在实际的问题中,不同通道的重要性可能是有差异的。SE模块可以通过对每一个特征层的信息分别建模,从而去自适应的重新定义每一个通道的重要程度。SE模块通过2步操作确定通道权重,Squeeze通过池化的方式将每个通道都提取出一个特征,Excitation通过学习的方式确定各个通道数的权重,最后将权重与对应的特征图相乘,SE结构如图4所示。

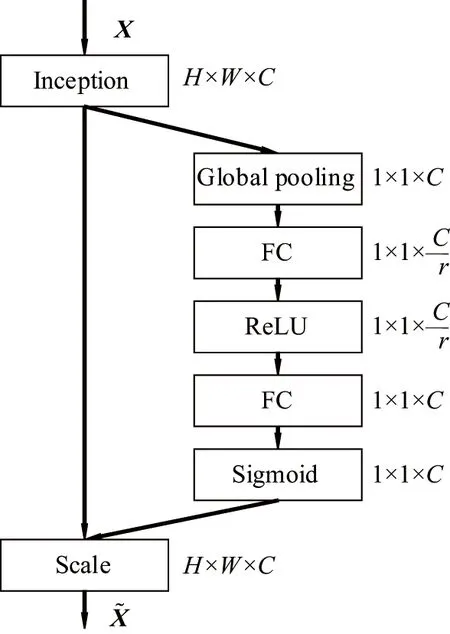
图4 SE结构Fig.4 SE structure

采用SoftPool[22]对空间金字塔池化(spatial pyramid pooling, SPP)[23]模块的MaxPool进行替换。SoftPool使用指数加权方式进行池化,相比与MaxPool直接使用最大值进行池化操作,SoftPool可以利用池化核的每个元素,只增加很少的内存占用,在提高对相似特征信息的识别能力的同时,保留了整个接受域的特征信息,可以在保持池化层功能的同时,尽可能减少池化过程中的信息损失,提高了算法的精度。SoftPool的核心思想是使用Softmax,根据非线性特征值计算区域的特征值权重为

(2)

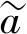
(3)

YOLOv5算法改进前后的性能比较如图5所示。从图5可见,使用KITTI公开数据集,训练经过200次迭代后,改进的YOLOv5算法的损失函数收敛值更小,同时准确率更高,说明了引入SE模块和Softpool模块能提高网络提取特征的能力,提升对小目标的检测能力。

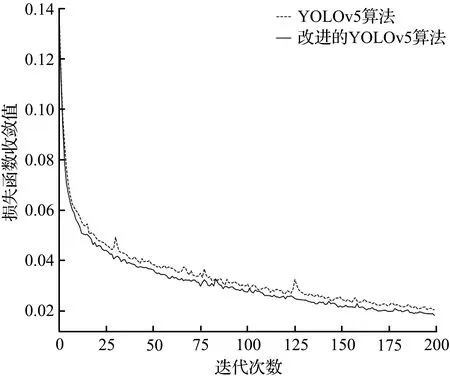
(a) 损失函数收敛值

2.3 运动场和目标检测的结合

运动场提取网络能够区分2帧图像中的动态物体和静态物体;但是这种区分不够精准,会出现不运动的物体以及零散的像素点被判断为运动对象的情况,所以单独使用该网络会造成过多的误判,影响静态特征点的提取。为了解决上述问题,在训练阶段和判断阶段结合了目标检测算法。

在训练之前,通过目标检测对潜在运动目标进行预检测,通过生成的Bounding Box获得二维边界信息,在训练过程中,利用边界信息设置残差平移场权重为

t(x,y)=t0+w(x,y)Δt(x,y),

(4)

式中：t为总平移场;t0为背景平移向量;w为权重,当像素点在Bounding Box内,则w=1,反之w=0;Δt为残差平移场。通过设置权重的方式可以提供给网络一定的先验信息,减少静态区域对训练的干扰。

在判断阶段,以目标检测生成的所有Bounding Box为候选区,记为Boxn,n为当前图像中Bounding Box的个数。当Boxi∈n中的动态像素点大于阈值,则判定该Box为动态区域,运动区域提取流程如图6所示。

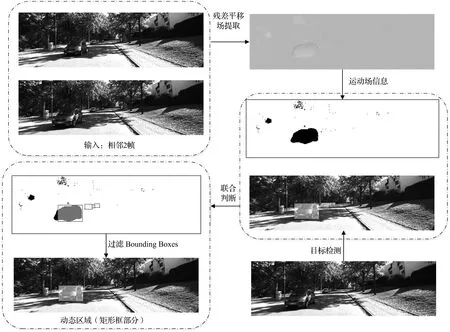
图6 动态区域提取流程Fig.6 Flow of dynamic region extraction

3 基于前向平移约束的误匹配点剔除算法

本文中的约束条件建立在摄像机位姿可以近似为只有平移环境的基础上,例如在直线道路居多的环境中。在该约束条件下,理想的一对匹配点应与极点(灭点)在同一直线上,下面对此做简要证明。假设相机从光心O1仅以平移的方式运动到光心O2,平移运动轨迹如图7所示。其中e和e′为灭点,他们在各自的像素坐标系中有相同的坐标,P和P′分别是在Pw投影下的像素坐标点。

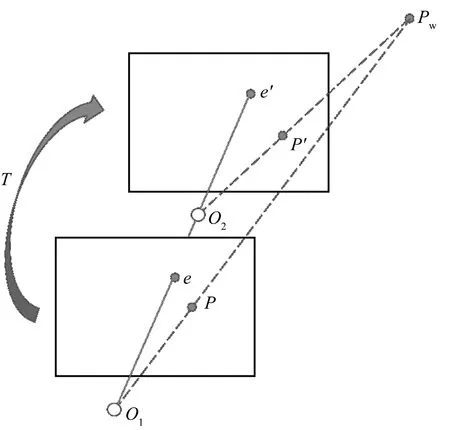
图7 平移运动轨迹Fig.7 Translational trajectory

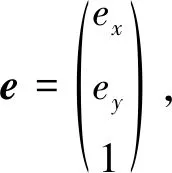
(5)

Pw以O2为世界坐标系原点的坐标为

(6)

则P′点的像素坐标为

(7)

由极几何可得

(8)

解得

(9)

由式(5)、式(7)、式(9)计算点e、P、P′三点一线：

(10)

由式(10)可知,在只有平移的情况下,匹配点对与灭点存在直线约束,但在实际情况下三点不能完全满足,因此在直线约束的基础上提出距离约束和角度约束来剔除误匹配点。在前向平移假设的情况下,相机主要沿着Z轴做平移运动,同时认为X、Y轴的位移忽略不计,则有

tz≫|tx|+|ty|≈0。

(11)

由式(5)、式(7)、式(9)可得灭点e分别与P和P′的欧氏距离,

(12)

式中z为P点世界坐标的Z轴数值,其大于在Z轴方向的位移tz,结合式(11)、(12)则有

d(e,P′)>d(e,P)。

(13)

由式(13)可得,在前向平移假设的情况下,距离约束为同名点在当前帧的像素坐标与灭点像素坐标的欧氏距离小于后一帧的欧氏距离。

对于角度约束,本文采用匹配点与灭点的夹角与阈值进行比较,并通过所有夹角的平均值得到阈值,以减少由灭点计算不准确和噪声带来的共有误差对算法准确度的影响。图8展示了某一特征点P基于前向平移约束算法剔除误匹配点的示意图,其中点e为灭点,在阴影区域之外的匹配点即为误匹配点。阴影区域是由射线eP向两侧偏移θ角形成的四边形eABC与扇形eDF的差集,其中θ和扇形eDF的半径分别为角度约束和距离约束的阈值。

对于第i(i>1)帧图像特征点P与第i-1帧匹配点P′基于前向平移约束匹配点剔除算法的具体步骤如下：

步骤1：计算图像灭点e像素坐标,若不存在则返回。

步骤2：计算第i-1到第i-N帧灭点坐标的离散程度,若大于阈值则返回。在本文中N取10。

步骤3：计算第i帧与第i-1帧所有匹配点与灭点的夹角平均值θavg,取阈值θthr=3θavg。

步骤4：取图像特征点P与第i-1帧特征点P的匹配点P′的像素坐标,若遍历完毕则返回。

步骤5：计算灭点e分别与点P和P′的欧氏距离分别为DI、Dthr,若DI

步骤6：若∠PeP′≥max(1°,θthr),则剔除该匹配点并执行步骤4。

步骤7：执行步骤4。

4 实验结果与分析

使用公共数据集KITTI、TUM对系统进行试验。KITTI数据集包含运动和静止的行人、车辆同时直线行驶部分较多,能够测试系统动静分离的能力和前向平移约束算法的效果;TUM数据集能够测试系统的深度学习算法部分在高动态环境下的性能和精度。本文与ORB-SLAM2、DynaSLAM系统进行了比较,选取了绝对轨迹误差(absolute trajectory error, ATE)和绝对位姿误差(absolute pose error, APE)指标对实验结果进行评估,采用了均方根误差(RMSE)、平均数(Mean)和标准差(STD)定量算法的精度。为了减少不确定因素的干扰,对每个序列运行10次取中值作为实验结果。试验环境配置为Ubantu18.04操作系统,Intel i7-9700处理器,NVIDIA GeForce RTX2070ti显卡的台式计算机。

4.1 SLAM系统评估

不同系统在KITTI数据集的ATE和APE比较如图9所示。从图9中可见,左列图像是ATE图,中间图像比较了真实轨迹和估计轨迹的x、y、z轴分量,右列图像定量比较了APE的平移部分,虚线表示真实轨迹,实线表示估计轨迹。SLAM系统将在动态物体上提取许多特征点,对定位和映射有影响。从图9中可见,随着运动场景逐渐变得复杂,单目SLAM的漂移误差越来越大,尤其ORB-SLAM2在02、08序列中存在着较大的尺度漂移,ORB-SLAM2在08序列最后一段序列中绝对轨迹估计失败;而在单目环境下,DynaSLAM将剔除图像中提取车辆或行人的特征点,无论它们是否在运动,导致特征点过少,造成位姿估算的精度下降。相比之下,由于减少了动态干扰和使用前向平移约束算法剔除误匹配点,本文中系统的尺度漂移相对较小,估计的轨迹相较于其他2种算法更加吻合。就APE而言,本文中系统的APE分别在0.1～14.2、2～70、0～115、1.8～13.0波动,然而,ORB-SLAM2的波动范围最大达到152以上,DynaSLAM的波动范围最大达到142以上。本文系统相较于ORB-SLAM2、DynaSLAM在波动范围上分别平均减少了21.25%、22.70%。

(a) ORB-SLAM2在KITTI数据集00序列指标

不同系统在数据集TUM的ATE比较如图10所示。从图10中可见,真实轨迹和ORB-SLAM2算法的轨迹之间的匹配精度几乎为0,其APE在序列fr3/w/xyz、fr3/w/half的波动范围分别为0.030～0.550、0～0.057,远远大于本文系统的0～0.057、0～0.220,同时本文提出的系统估计轨迹更接近真实轨迹,鲁棒性更强。

(a) ORB-SLAM2在TUM数据集fr3/w/xyz序列指标

不同系统的特征点提取比较如图11所示。从图11中可见,ORB-SLAM2不区分动静物体,在运动物体上也提取了一部分的特征点,导致算法精度降低。从特征点提取结果对比可以得出本文系统能较好地减少动态物体对定位的干扰。

(a) 本文算法

ATE由估计位姿和真实位姿的差值得到,可以比较直观地反映算法精度和轨迹的全局一致性。第i帧的ATE定义为

(14)

式中：Qi、Pi分别为第i帧的真实位姿、估计位姿;S为估计位姿到真实位姿的转换矩阵。ATE的均方根误差定义为

(15)

式中trans(Ei)为APE的平移部分。

不同系统在单目环境的RATE比较见表1(粗字体表示结果最优),不同系统在RGB-D环境的RATE、Mean、STD比较见表2(粗字体表示结果最优)。

表1 不同系统在单目环境的RATE比较Tab.1 Comparison of RATE for different system

表2 不同系统在RGB-D环境的RATE、Mean、STD比较Tab.2 Comparison of RATE、Mean、STD of different systems in RGB-D environment

均方根误差衡量估计轨迹与真实轨迹之间的偏差,能更好地反映系统的鲁棒性;平均值反映该组绝对轨迹误差总体的一般水平,或分布的集中趋势;标准差反映绝对轨迹误差自身的离散程度,能够反映系统的稳定性。表1中System(D)表示仅使用深度学习算法识别动静区域的系统,System(F)表示仅使用前向平移约束算法来剔除误匹配点的系统,System(D+F)表示深度学习和前向平移约束算法都使用的系统。在KITTI中对使用深度学习和前向平移约束算法的系统(D+F)在大多数序列中是最准确的。System(D)主要改进了对运动区域的划分,在高动态的TUM序列中表现较好。System(F)在直线场景丰富的序列中准确度尚可,同时可以剔除系统(D)中无法剔除的SLAM系统自身产生的误匹配点,但是在直线场景较少的序列如KITTI09或是车辆行驶过程抖动剧烈如序列KITTI08,都会影响算法的准确性,同时有可能退化为原始算法甚至对位姿估计产生干扰。总体上,在2种环境下本文系统要优于ORB-SLAM2和DynaSLAM,优化效果I计算式为

(16)

式中：Rour为本文系统的轨迹误差;Roth为其他系统的轨迹误差。在KITTI序列中System(D+F)的RATE较ORB-SLAM2和DynaSLAMR的分别平均降低了16.38%、6.65%;System(D)在TUM单目环境下的RMSE较ORB-SLAM2和DynaSLAM的分别平均降低了57.35%、6.47%,在表2中System(D)的RATE较ORB-SLAM2和DynaSLAM的分别平均降低了84.26%、8.32%。3种系统在TUM单目环境的跟踪定位成功率见表3(粗字体表示结果最优)。从表3可见,本文系统相较于ORB-SLAM2可以大幅提高跟踪定位成功率,因为ORB-SLAM2对“fr3/w/static”和“fr3/w/xyz”序列只有30%左右的成功率,故在表1中未给出ORB-SLAM2在该2个序列中的RMSE数据。

表3 3种系统在TUM单目环境的定位成功率Tab.3 Localization success rate of different systems in monocular environment %

4.2 算法效率评估

本文对各系统算法效率进行了比较,通过使用GPU同时采用批处理操作加快了深度神经网络输出运动场的速度,提高了整个系统的时间效率。3种系统在不同环境中的平均每帧处理时间见表4。在GPU环境下,System(D+F)相较DynaSLAM速度提升了4.6倍,整体运行速度达到帧率约为9 s-1,在CPU环境下也提升了约5.3倍。

表4 平均单帧处理时间Tab.4 Average single frame processing time s

5 结语

SLAM系统进行位姿估计的过程中,由于动态物体的干扰会影响其位姿估计的精度,因此本文提出一种SLAM结合深度学习算法,主要工作如下：

①引入无监督的深度估计网络,利用动态区域不同于静止区域的位姿,通过重构图像损失,以像素级的方式输出运动场信息,同时针对网络误判率较高的问题,使用目标检测网络对训练数据预处理,以减少误判率。

②提出了前向平移约束的误匹配特征点对筛除算法,进一步筛除误匹配特征点。

③对YOLOv5网络模型进行改进,引入注意机制模块,以提高模型的特征提取能力和检测精度。此外,在SPP模块中引入了SoftPool,以改进池化操作,并保持更详细的特性信息,使得网络增加对小目标的识别能力。

然而目前本文算法相较原系统增加了许多额外的时间开销,运动场的提取存在错检和漏检。未来的工作方向主要是简化神经网络结构以提升计算速度,强化深度学习网络提取动态物体特征的能力;提高前向平移约束算法提取灭点的准确度以及设计在道路转弯环境中的异常匹配点剔除算法,以进一步提升算法精度和适用性。