并列相邻桥梁气动干扰对车桥耦合振动的影响研究

郭向荣，肖一凡

(中南大学 土木工程学院，湖南 长沙 410075)

为同时满足公路和铁路运输需求，新建公铁两用桥梁渐渐成为了一种趋势[1]。新建公铁两用桥梁主要有公铁合建和公铁分建双梁2种形式。公铁合建形式可以提高桥梁刚度，充分利用桥位资源，节省成本资源，然而，使用此种方案时，公路和铁路的线型相互影响，两岸接线复杂[2]，同时，运营和养护期间，铁路和公路相互影响，甚至会造成较大的维护费用。而公铁分建双梁形式不受线型控制，同时，可以避免公路车辆对铁路线路的影响，减小安全隐患，运营维护更为方便[3]，因此此形式被广泛使用于工程界。然而采用公铁分离桥梁形式时，并列相邻桥梁之间的气动干扰导致其周围流场与单铁路主梁周围流场不同[4]，横风作用下列车-桥梁耦合振动也较单铁路主梁不同。目前，众多学者对并列相邻桥梁气动干扰开展了研究。IRWIN 等[5]以新建塔科马桥为研究对象，通过节段模型和全桥气弹模型风洞试验，研究了并列桥梁之间的气动干扰。陈政清等[6-7]分别对并列主梁的气动力系数和颤振性能进行了研究，结果表明并列相邻桥梁之间存在一定的气动干扰，并列相邻桥梁的相对宽度对桥梁颤振稳定性有影响。罗士瑾等[8]研究了并列桥梁气动干扰对主梁的涡振性能的影响，结果表明风向会导致并列桥梁气动干扰对主梁产生不同的影响。刘慧杰等[9]利用数值模拟得到了并列双钝体箱梁周围的流场分布，研究了并列桥梁气动力的干扰机理，得到了并列箱梁之间产生的漩涡导致了阻力系数变化的结论。严乃杰等[10]通过节段模型风洞试验，得到了考虑和不考虑既有桥梁干扰下的车桥系统的气动三分力系数，结果表明既有桥梁干扰使得部分工况下列车的三分力显著增大，既有桥梁的干扰对相邻桥梁的影响不可忽略。既有研究多针对平行双幅桥梁涡振、颤振性能和车桥系统气动力开展工作，少有学者进行并列相邻桥梁气动干扰对列车桥梁系统耦合振动影响的研究，然而对于铁路桥梁来说，满足列车运行安全性和舒适性是一项重要设计指标，因此非常有必要进行该项研究。本文利用数值模拟方法得到了考虑、不考虑并列桥梁气动干扰的车桥系统气动三分力系数，分析气动干扰对车桥系统三分力系数的影响，建立风车桥耦合振动方程，计算考虑、不考虑并列桥梁气动干扰下车桥动力响应，研究并列桥梁气动干扰对车桥耦合振动的影响。

1 工程概况

本文选取重庆市涪陵区某公铁分建斜拉桥为研究对象，该桥桥塔为双菱形联体桥塔，公路和铁路主塔在下横梁及其上下部的一段塔柱区域内连接在一起，桥跨布置为4×56+608+4×56 m，桥梁立面布置图见图1。上游为双向6车道分离式双箱公路梁，桥面宽38 m，高3.5 m，公路梁主梁断面图见图2，下游为双线铁路梁，采用钢混组合梁截面，桥面宽23.6 m，高4.5 m，铁路梁主梁断面图见图3。铁路梁与公路梁中心间距42.7 m，桥面高差1 m。

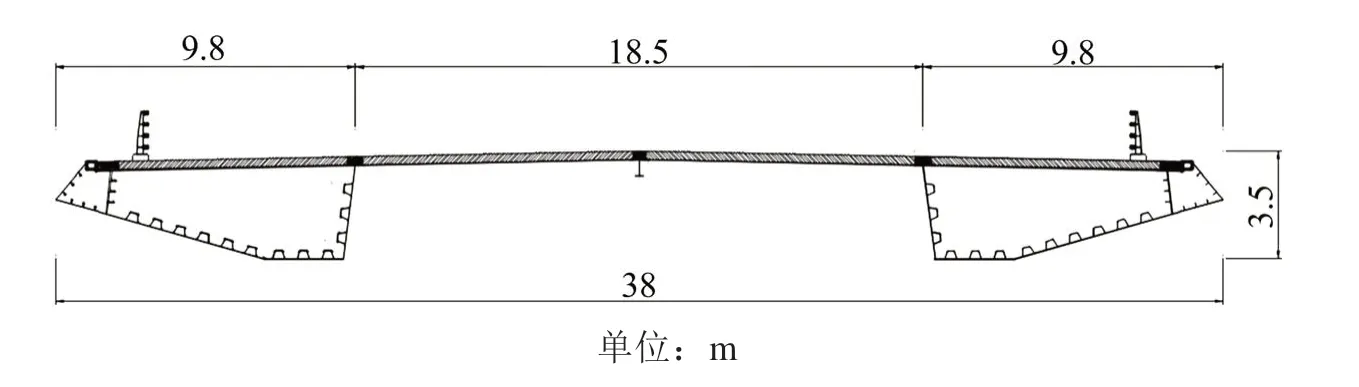
图2 公路梁截面Fig.2 Section view of highway beam

图3 铁路梁截面Fig.3 Section view of railway beam

2 三分力系数计算

本文针对不同来流方向(铁路主梁迎风、公路主梁迎风)的并列桥梁和单铁路主梁工况，考虑不同列车行车位置(迎风、背风、双线)，对列车、桥梁的气动三分力系数进行了计算。表1展示了数值模拟计算工况。

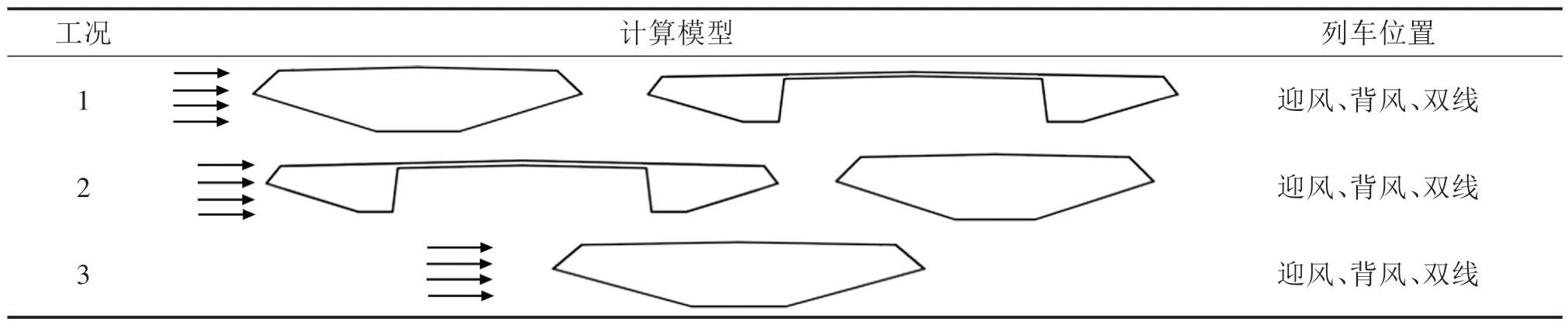
表1 数值模拟工况Table 1 Numerical simulation conditions

取主梁和CRH 3 型列车1︰50 缩尺模型在0 度风攻角下进行二维建模，湍流模型采用SSTk-ω模型[11]，利用FLUENT进行计算，计算域上下边界至模型距离取5B(B为梁宽)，计算域进口至模型距离取5B，出口至模型距离取20B。由于列车及桥梁截面的复杂性，本文采用非结构网格，为了准确模拟壁面效应，网格在车桥模型表面加密，为满足无量纲数y+=1，第1 层网格厚度定为0.02 mm。流场入口设置为速度边界，并设置来流风速20 m/s与风洞试验相同，流场上下边界均设置为对称边界，出口设置为压力边界，主梁与列车外壁定义为非滑移壁面边界。

为了验证数值模拟的准确性，在中南大学风洞高速实验段进行了单铁路主梁节段模型测力实验。试验模型比例为1︰50，模型外形据实桥严格按几何缩尺比缩小，保证几何相似。为避免端部效应，在模型两端设置了端板。桥梁与列车两端通过ATI Delta 六分量动态测力天平采集三分力数据，分辨率为0.02 N，采样频率为1 kHz。参考风速采用澳大利亚TFI公司的眼镜蛇探针测量，参考点位于模型上游1.5 m 处，高度与主梁顶面高度一致。试验模型图如图4。

图4 车桥系统节段模型Fig.4 Segment model of vehicle-bridge system

表2将单铁路主梁双线工况桥梁与列车的三分力系数数值模拟结果与风洞实验结果进行了对比，括号中数据代表数值模拟结果与风洞试验结果的差异。

表2 数值模拟结果与风洞试验结果对比Table 2 Comparison of numerical simulation results with wind tunnel test results

由表2可知，阻力系数模拟值与试验值最大相对误差为7%，升力系数模拟值与试验值最大相对误差为6.3%，二者的模拟值与试验值吻合较好，虽然扭矩系数模拟值与试验值差异百分比较大，但由于扭矩系数绝对值较小，且较小的扭矩系数对车桥耦合振动响应贡献很小[12]，因此可以忽略此差异。由于单主梁三分力系数与双主梁三分力系数从断面流场计算角度考虑本质上是一致的[13]，说明本文数值模拟方法在计算三分力系数的精度时是可靠的。

采用上述的数值模拟方法计算表1 中3 个工况得到的铁路梁和列车三分力系数结果如表3 及表4，括号中数据代表此系数与工况3 中此系数的差异。

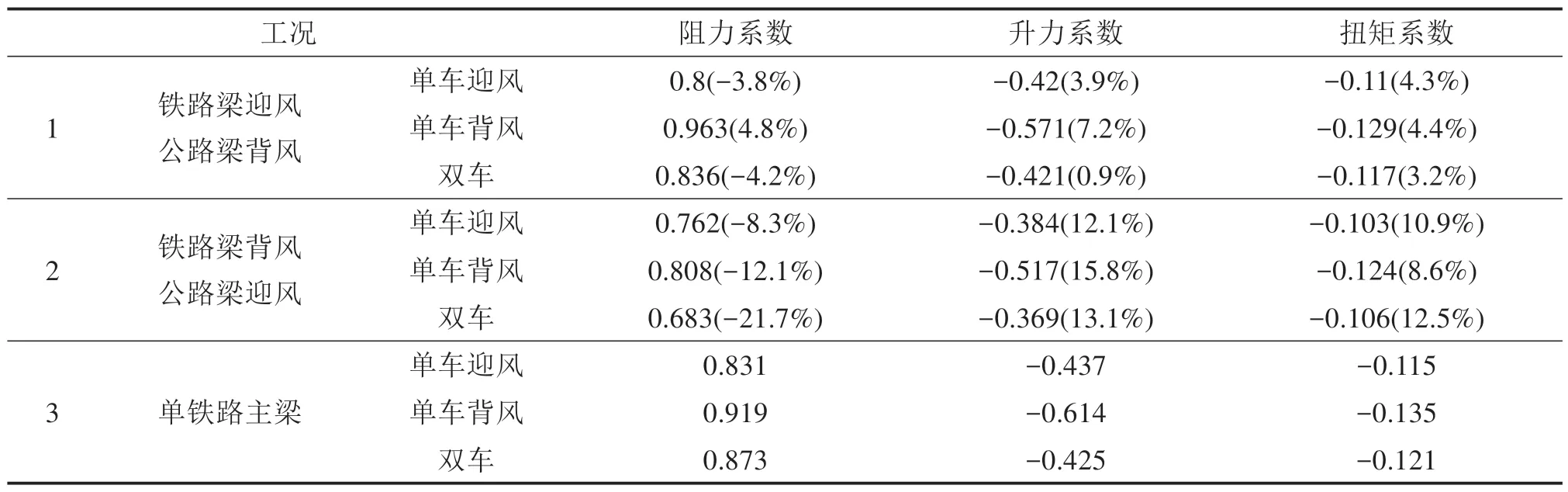
表3 铁路梁三分力系数Table 3 Three component coefficients of railway beam

表4 列车三分力系数Table 4 Three component coefficients of highway beam

由表3 可知，对比工况1 与工况3 桥梁的三分力系数，考虑并列桥梁气动干扰且铁路梁为迎风侧时，公路梁对铁路梁三分力系数的影响很小，单车背风工况桥梁阻力系数增幅最大，为4.8%，此工况下桥梁升力系数增大7.2%。对比工况2 与工况3桥梁的三分力系数，考虑并列桥梁气动干扰且铁路梁为背风侧时，铁路梁阻力系数显著减小，双车工况桥梁阻力系数减幅最大，为21.7%；铁路梁升力系数显著增大，最大增幅为15.8%；铁路梁的扭矩系数均减小，最大减幅12.5%。

由表4 可知，工况1 与工况3 列车三分力系数基本相同，考虑并列桥梁气动干扰且铁路梁为迎风侧时，公路梁作为下游桥梁对上游的列车基本无影响。对比工况2 与工况3 的列车三分力系数，考虑并列桥梁气动干扰且铁路梁为背风侧时，列车的阻力系数显著增大，单车背风工况增幅最大，为31.7%；列车的升力系数均减小，最大减幅9%；列车的扭矩系数均增大，最大增幅13.4%。

由模拟结果可知，若考虑并列桥梁的气动干扰，车桥系统三分力系数与单铁路主梁车桥系统三分力系数有一定差距，尤其对于铁路梁为背风侧的并列桥梁工况，桥梁的三分力系数减小而列车的阻力系数显著增大，不利于列车的行车安全性。

3 风-车-桥耦合振动模型

3.1 桥梁有限元模型

本文桥梁模型采用空间梁-板-索有限元分析模型，主梁、桥塔、桥墩采用2 节点12 自由度梁单元，桥面板采用4 节点8 自由度板单元，斜拉索采用2 节点6 自由度索单元[14]，桩基础采用m 法考虑桩土共同作用，桥梁的有限元模型如图5。桥梁的阻尼采用瑞利阻尼考虑，桥梁阻尼比取5‰。

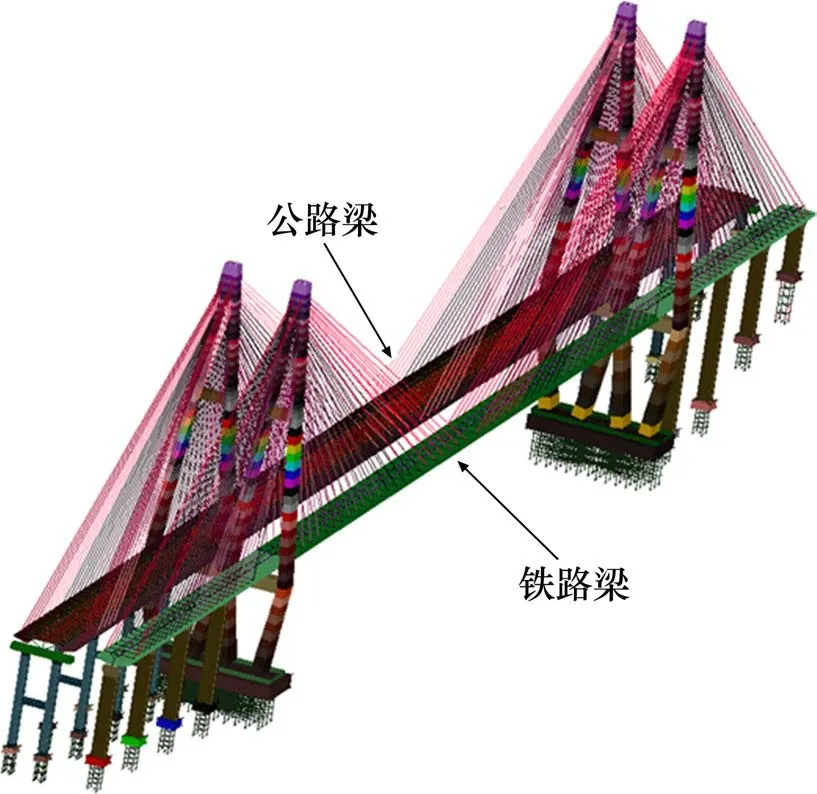
图5 桥梁有限元模型图Fig.5 Finite element model of the bridge

3.2 车辆模型

本文以CRH3型高速列车为研究对象，以多刚体动力学方法建立车辆模型。列车模型由1 车体、2 构架、4 轮对共7 个刚体及一系、二系悬挂组成。为了提高计算效率，在不失精度的前提下做如下假定[15]：1) 忽略所有刚体的纵向自由度；2) 仅考虑轮对的侧摆和摇头自由度；3) 所有弹簧均为线性弹簧，阻尼为黏滞阻尼；4) 轮轨竖向为密贴关系，轮轨蠕滑力按Kalker 线性理论计算。基于以上假定，一节4轴列车共有23个自由度。

3.3 风-车-桥耦合振动方程建立

本文将列车桥梁视为一个整体系统，以各单体结构静力平衡位置为坐标原点，桥梁的边界条件即为此系统的边界条件，计算车辆惯性力做功负值、车辆阻尼器阻尼力做功负值、车辆弹簧应变能、轮对重力刚度引起的势能和车辆重力势能并将之相加得到车辆空间振动总势能，同理计算得到桥梁空间振动总势能，将桥梁和列车在任意时刻的动力学总势能相加，利用弹性系统动力学总势能不变值原理[16]和形成矩阵的“对号入座”法则，将轨道不平顺视为内部激励、风荷载作为外部激励，建立风-车-桥耦合系统振动方程如式(1)，因以桥梁静力平衡位置为原点，荷载列阵仅由列车重力及风荷载组成。基于自编软件利用逐步积分法求解风-车-桥耦合振动方程[17]。

式(1)中：Xb，，为桥梁位移、速度、加速度；Xt，，为列车位移、速度、加速度；Mb，Mt，Cb，Ct，Kb，Kt分别为桥梁与列车的质量矩阵、阻尼矩阵、刚度矩阵；Cbtb，Ctb，Kbtb，Ktb分别为车桥耦合系统中由桥梁振动速度引起的阻尼矩阵和刚度矩阵；Cbt，Ctt，Kbt，Ktt分别为车桥耦合系统中由列车振动速度引起的阻尼矩阵和刚度矩阵；Pbw，Ptw为作用于桥梁和列车上的风荷载向量；Pbe为列车各自由度自重荷载向量；Pg为作用于公路桥上的汽车荷载，由于本桥设计方案为公铁分建双梁形式，汽车桥梁耦合振动对列车-铁路梁系统振动影响不大[18]，因此按照《JTG D60―2015》公路桥梁设计规范中均布荷载和集中荷载来模拟车道荷载进行加载。

式(1)中风荷载向量由静风荷载及抖振力荷载组成。静风荷载包括阻力、升力及升力矩。抖振力荷载由作用于桥梁上的脉动风引起，脉动风场可由顺桥向桥梁各点脉动风时程曲线叠加而成[19]，同时，已有研究表明脉动风最不利方向为垂直于列车前进方向[20]，因此，本文在考虑各模拟点的空间相关性下[21-22]，依据我国《公路桥梁抗风设计规范》中给出的脉动风功率谱密度函数，采用谐波合成法模拟了沿桥梁纵向间距为20 m 的各点的一维横向脉动风场，如图6 所示，模拟时间间隔为0.1 s，各桥梁节点受到的脉动风按相邻的2 个风速模拟点线性内插得到。因此，桥梁第i个节点由风产生的横向力如式(2)。

图6 平均风15 m/s时桥梁起点处脉动风时程曲线Fig.6 Simulated wind speed curve at starting point of bridge under 15 m/s average wind speed

式中：W为第i个节点的来流风压；H为桥梁高度；L为梁段长度；Cd为阻力系数；Ui为平均风速度；ui(t)为脉动风速；v为桥梁振动速度；ρ为空气密度，取1.225 kg/m3。

忽略与Ui无关的微量项，此式即为：

式(3)中：1/2×ρ×Ui2×H×L×Cd项即为静风荷载，1/2×ρ×2×Ui×ui(t) ×H×L×Cd项即为脉动风抖振力荷载，1/2×ρ×2×Ui×v×H×L×Cd项为空气动力阻尼项，可归入结构阻尼矩阵。同理，桥梁第i个节点由风产生的升力、扭矩如式(4)。

式(4)中：B为桥梁高度；Cl和Cm为升力系数和扭矩系数。列车受到的静风荷载与抖振风力计算原理与桥梁一致。

3.4 车桥耦合振动模型的验证

为验证本文模型的正确性，针对上述模型，选取同文献[22]同样的参数和计算条件计算了列车以374 km/h 通过简支梁桥的动力响应。图7是桥梁首跨跨中竖向加速度时程曲线，横坐标为列车运行距离与简支梁跨度之比，对比文献[22]中图10的结果，可以看到二者在趋势和幅值上基本一致，证明了本文模型是正确的。

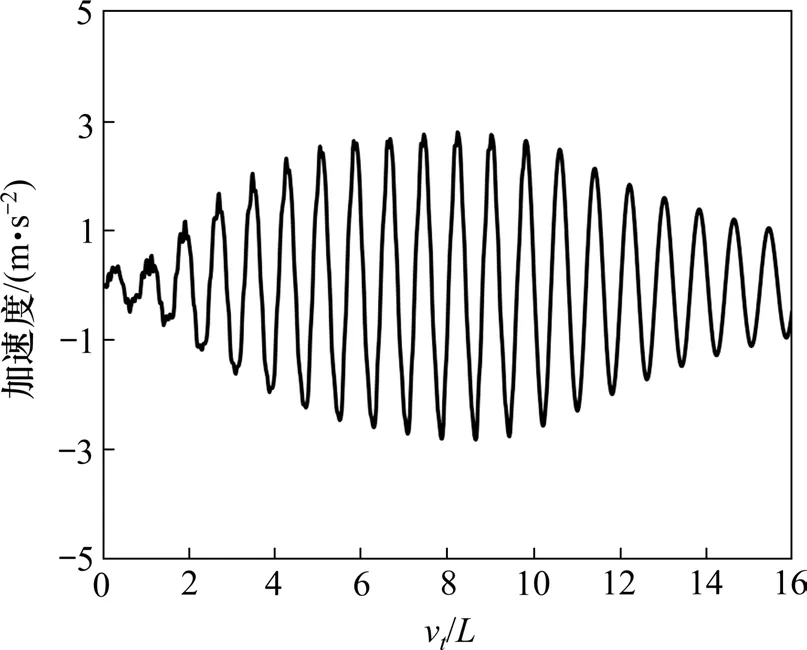
图7 简支梁首跨跨中竖向加速度Fig.7 Midpoint vertical acceleration of the first beam

4 结果分析

基于以上的风-车-桥耦合振动模型，对于考虑不同来流方向(铁路主梁迎风、铁路主梁背风)的并列桥梁和单铁路主梁3种工况，分析列车在不同风速(15，20 和25 m/s)下以不同车速(250，275，300，325 和350 km/h)通过时桥梁和列车的动力响应。计算使用的轨道不平顺包括随机轨道不平顺和附加轨道不平顺，以德国低干扰谱模拟随机轨道不平顺，叠加桥梁升温和徐变变形的附加轨道不平顺。

4.1 不同工况下桥梁响应

桥梁跨中横向位移最大值随风速、车速变化趋势如图8。由图8 可知，桥梁跨中横向位移随车速和风速的增加而增大，工况2(铁路梁为背风侧)下桥梁横向位移显著大于工况3(仅考虑单铁路主梁)，工况1(铁路梁为迎风侧)下桥梁横向位移与工况3 相差不大。工况2 较工况3 的桥梁横向位移增幅随着风速和车速的增加而增大，增幅由8%增大至13.7%，而工况1 与工况3 的桥梁横向位移差异随着风速和车速的增加而基本不变，最大变化幅值为3.6%。

图8 桥梁跨中横向位移最大值Fig.8 Maximum lateral displacement of bridge

桥梁跨中竖向位移最大值随风速、车速变化趋势如图9。由图9 可知，桥梁跨中竖向位移随车速和风速的增加而增大，工况1 和工况2 下桥梁竖向位移与工况3相差不大。工况1，工况2与工况3的桥梁竖向位移差异随着风速和车速的增加而减小，由1.92%减少到0.73%。

图9 桥梁跨中竖向位移最大值Fig.9 Maximum vertical displacement of bridge

风速为25 m/s，车速为250 km/h时，不同行车工况下桥梁跨中横向位移、竖向位移最大值如表5，括号中数据代表此系数与工况3 的差异。对比工况2 与工况3 结果，对于单线迎风行车和双线行车，工况2 的桥梁跨中横向位移显著大于工况3，最大增幅为10.9%，单线背风行车对桥梁跨中横向位移基本无影响，行车工况对桥梁竖向位移基本无影响；对比工况1 与工况3 结果，单线背风行车工况时工况1 桥梁横向位移较工况3 增大5.9%，其余行车工况对桥梁横向位移和竖向位移基本无影响。

表5 不同行车工况桥梁跨中位移最大值(风速25 m/s，车速250 km/h)Table 5 Maximum mid-span displacement of bridge under different conditions (wind speed at 25 m/s,train speed at 250 km/h)

4.2 不同工况下列车响应

3 种工况下列车的脱轨系数、横向力和横向加速度最大值随风速、车速变化趋势分别如图10～12。由图可知，列车的脱轨系数、轮轨横向力和横向加速度随车速和风速的增大而增大。工况2(铁路梁为背风侧)下列车的脱轨系数、横向力和横向加速度均较工况3(仅考虑单铁路梁)显著增大。工况2 与工况3 的列车脱轨系数和轮轨横向力增幅随风速和车速的增大基本不变，列车的脱轨系数最大增幅为14.28%，列车的轮轨横向力最大增幅为28.04%；工况2 较工况3 的列车横向加速度增幅随风速的增大而显著增大，15 m/s风速时最大增幅为2.4%，25 m/s风速时最大增幅为16.67%。工况1(铁路梁为迎风侧)下列车的脱轨系数、轮轨横向力和横向加速度均较工况3基本不变。

图10 不同工况下列车的脱轨系数最大值Fig.10 Maximum derailment coefficient of trains under different conditions

图11 不同工况下列车的轮轨横向力最大值Fig.11 Maximum wheel-rail lateral force of trains under different conditions

图12 不同工况下列车的横向加速度最大值Fig.12 Maximum lateral acceleration of trains under different conditions

风速为25 m/s，车速为250 km/h时，不同行车工况列车动力响应最大值见表6，括号中数据代表此系数与工况3 的差异。由表6 可知，工况2 下列车的动力响应较工况3 显著增大，工况1 下列车的动力响应较工况3基本不变；当列车行车工况为双线行车时，工况2 较工况3 的列车动力响应增幅最大，脱轨系数最大增幅13.6%，轮轨横向力最大增幅28%，横向加速度最大增幅16.7%。

表6 不同行车位置不同工况下列车动力响应最大值(风速25 m/s，车速250 km/h)Table 6 Maximum train dynamic response under different conditions (wind speed at 25 m/s,train speed at 250 km/h)

5 结论

1) 考虑并列桥梁的气动干扰效应，且当铁路梁为迎风侧时，车桥系统的三分力系数与单铁路主梁工况基本相同；当铁路梁为背风侧时，车桥系统的阻力系数变化最为明显，铁路梁的阻力系数与单铁路主梁工况相比减小，最大减幅为21.7%，桥梁升力系数和扭矩系数均增大，列车的阻力系数增大，最大增幅为31.7%，升力系数减小，扭矩系数增大。

2) 考虑并列桥梁的气动干扰效应，当铁路梁为迎风侧时，列车通过桥梁，桥梁的横竖向位移与单铁路主梁相比差距不大；当铁路梁为背风侧时，桥梁的横向位移与单铁路主梁工况相比显著增大，桥梁的竖向位移与单铁路主梁工况相比基本相同，双线行车工况较其他行车工况下桥梁横向位移增幅更大。

3) 考虑并列桥梁的气动干扰效应，当铁路梁为迎风侧时，列车通过桥梁，列车的动力响应与单铁路主梁工况相比基本相同；当铁路梁为背风侧时，列车的动力响应与单铁路主梁工况相比显著增大，且列车的横向加速度增幅随风速的增大而显著增大，双线行车工况较其他行车工况下列车响应增幅更大。

4) 并列桥梁的气动干扰对车桥耦合振动响应不容忽略。当铁路梁为背风侧时并列桥梁的气动干扰效应更为明显。当环境风速越大时，更应该考虑气动干扰对车桥耦合振动的影响。