基于隐式动力方法的大跨混凝土薄壳结构弹塑性全过程分析
杨成栋, 黄永强,2, 闫泽升
(1 华建集团华东建筑设计研究院有限公司,上海 200002;2 上海超高层建筑设计工程技术研究中心,上海 200002)
0 引言
混凝土壳体结构在形态上更符合力学概念,将弯矩转化为薄膜内力,能充分利用混凝土抗压强度大的特点;因其造价低、厚度小、跨度大得到广泛应用。然而随着建筑造型越来越大胆、创新,壳体结构造型及受力也就越来越复杂,因此对薄壳结构的性能分析也就越发重要。
此时,传统的力学分析方法难以发现结构设计中存在的一些问题;采用有限元法进行薄壳结构的非线性全过程分析,则是预测结构承载力及受力性能的有效手段[1-2]。
1 工程概况
第十届中国花卉博览会世纪馆为体现建筑的轻盈、灵动,屋面采用大跨混凝土薄壳结构。壳面采用250mm厚C40混凝土,跨度在24~30m范围,矢跨比约为1/16~1/10;屋面支撑在周边剪力墙与摇摆柱上,为平衡拱壳的水平反力,在剪力墙面外设置翼墙,摇摆柱顶设置预应力混凝土环梁。东西区中间为26m跨度的中央通道,由四道张弦桁架形成自平衡体系,结构体系及布置见文献[3]。
2 弹塑性分析方法
由于混凝土损伤会导致其发生强度退化和刚度软化,尤其是复杂结构中常会出现混凝土受压区和受拉区耦合的情况[4],采用隐式计算的牛顿迭代时常会出现数值不收敛的问题。此时通常采用显示时间积分算法(即中心差分法),显示积分算法无需迭代,能解决数值收敛问题;但采用显示时间积分算法时,存在累积误差和动力效应相互影响放大的问题。因此为了平衡效率与精度的矛盾,本文采用ABAQUS提供的隐式动力分析方法(implicit dynamic analysis)中的准静态方法(quasi-static),该方法采用的是向后欧拉迭代算法。相比于牛顿迭代法,隐式动力方法的惯性效应能提高数值计算的稳定性,故其收敛性较好[5]。
2.1 计算模型
采用ABAQUS6.13进行整体模型在竖向荷载下的弹塑性分析。有限元模型通过SAP2000导入,剪力墙和屋面壳体采用S4R/S3R壳单元,洞口边梁、悬挑梁采用B31梁单元,摇摆柱采用T31桁架单元来模拟两端铰接。混凝土壳内钢筋分区采用rebar的形式考虑,配筋信息及钢筋方向均与SAP2000弹性计算模型保持一致;对于型钢混凝土梁,内部型钢单独采用梁单元与混凝土单元通过共节点的形式共同作用。世纪馆整体有限元模型如图1所示。
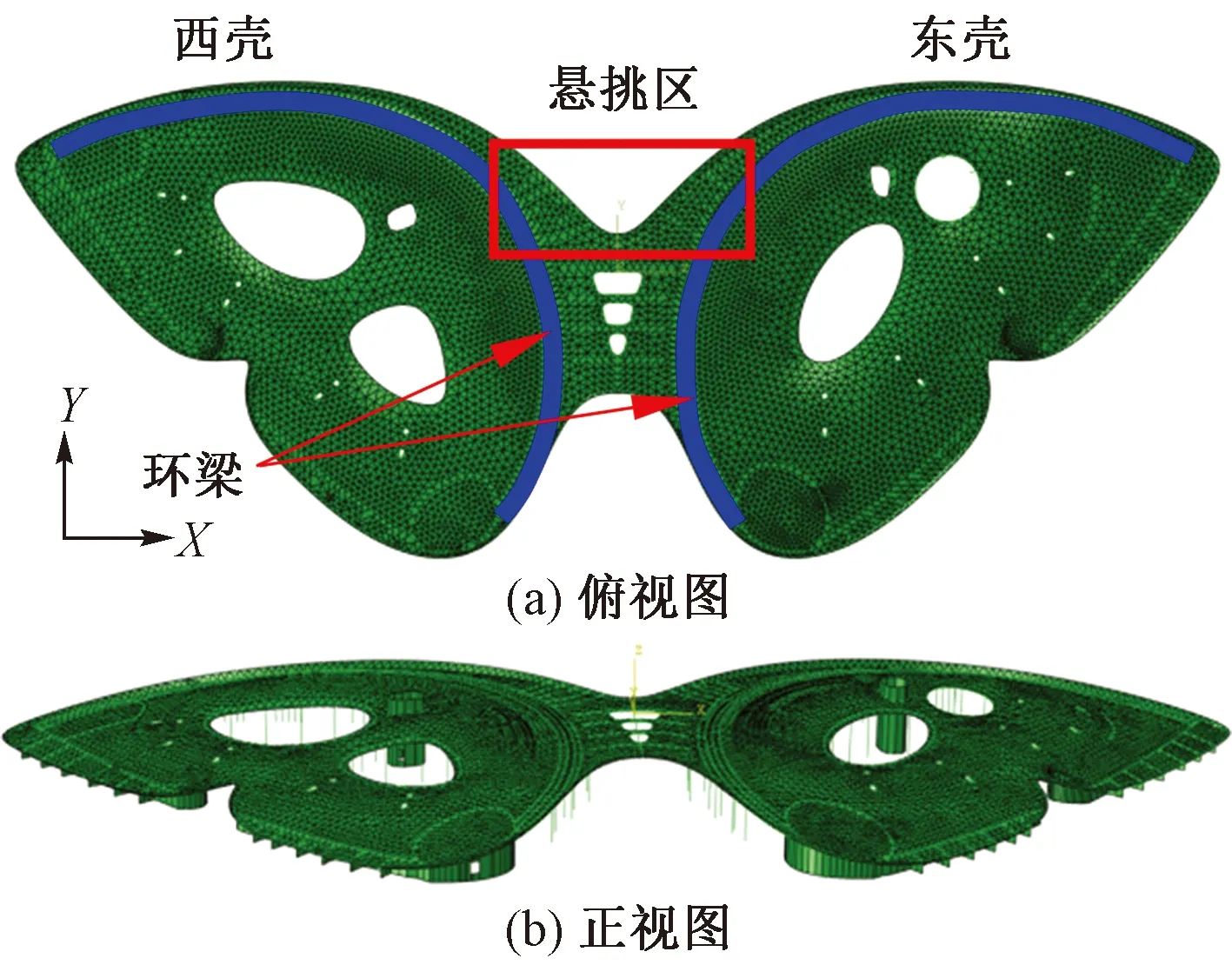
图1 世纪馆有限元计算模型
屋面附加恒载SD为7kN/m2,活载L为3kN/m2,此外还考虑-9℃的温度荷载。环梁预应力筋施加预应力774MPa,张弦桁架的弦杆施加预应力65MPa;本文采用的预应力的施加方法是初始预应力法,由于模型是从SAP2000导入,无几何信息,若采用降温法则只能施加于节点,使得预应力下混凝土损伤偏大,与实际不符。
2.2 材料本构
弹塑性分析的材料强度均采用强度标准值。混凝土材料采用ABAQUS提供的CDP本构模型,混凝土单轴受拉、受压应力-应变曲线见图2、3,其单轴应力-应变曲线表达式如下所示[6-7]:
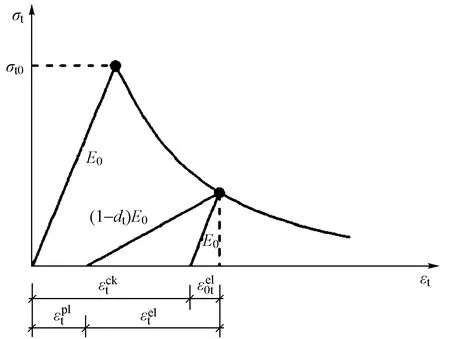
图2 混凝土单轴受拉应力-应变曲线
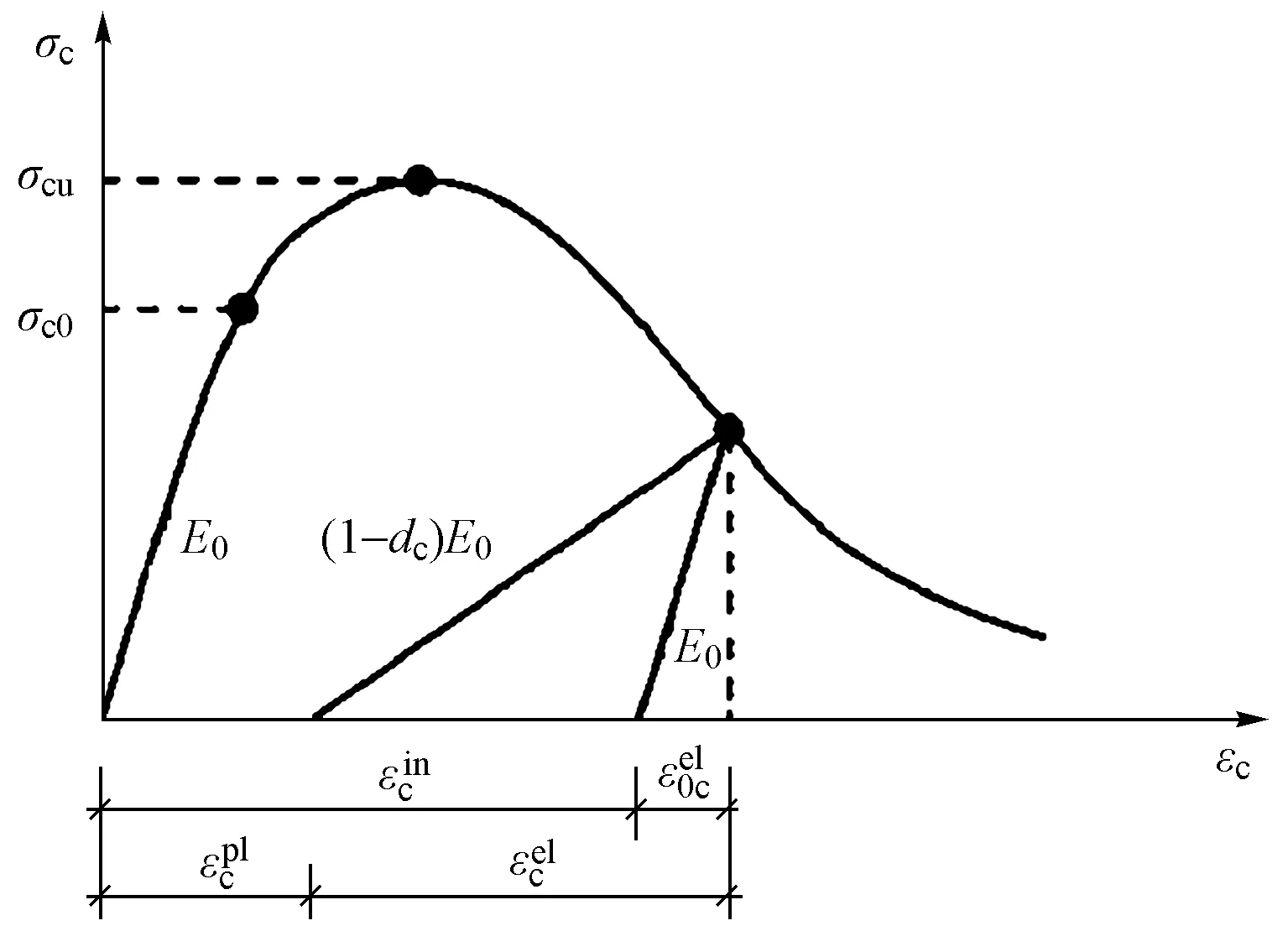
图3 混凝土单轴受压应力-应变曲线
(1)
(2)
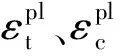
本文采用Najar损伤理论计算损伤因子(即损伤演化参数),该理论认为能量的耗散过程或者不可逆的热力学过程即为其损伤的实质[8],Najar理论损伤示意图见图4。文献[9]表明该计算模型公式简单、精度较高,能揭示实际情况中材料的损伤程度和结构破坏的宏观关系。
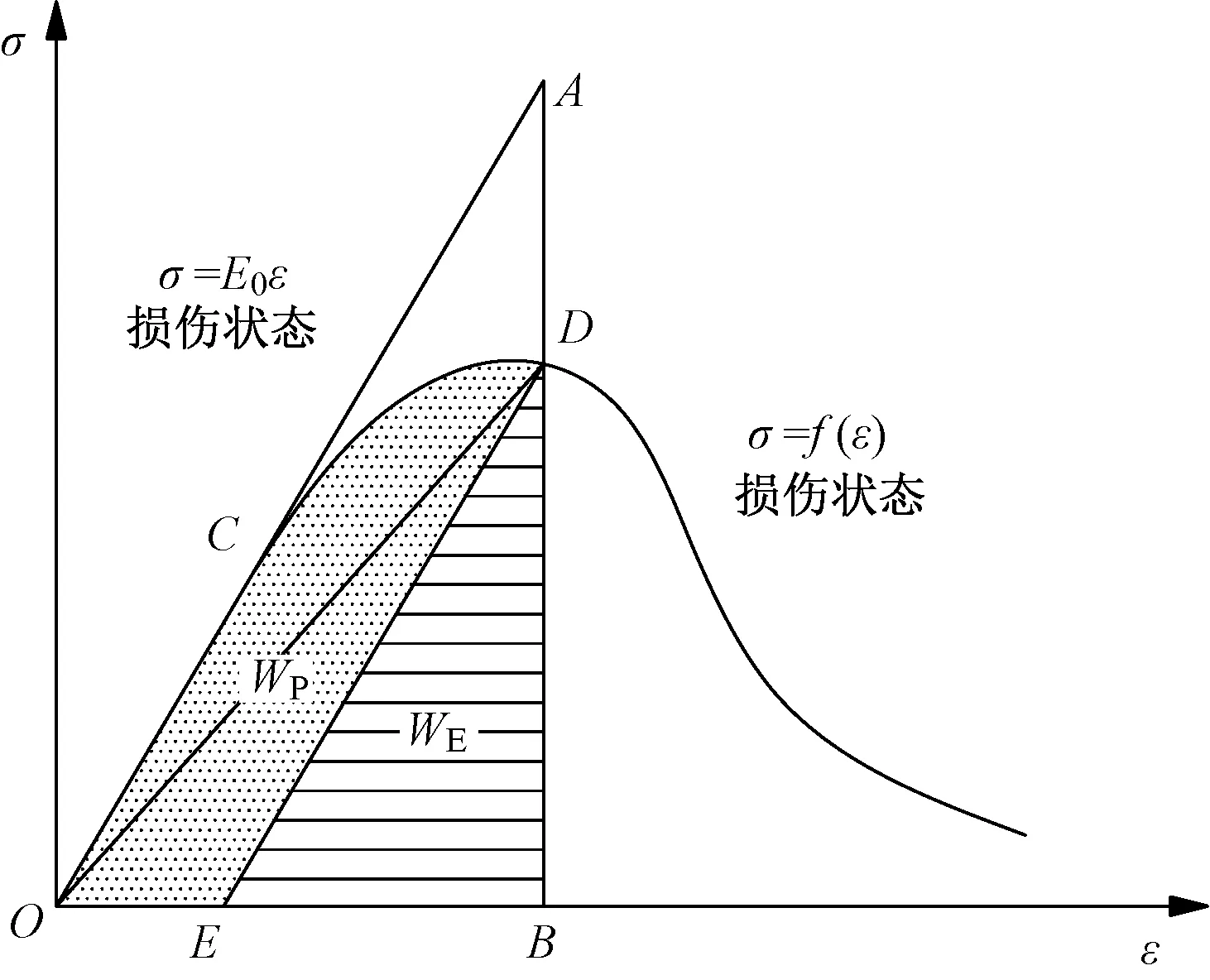
图4 Najar理论损伤示意图
基于Najar损伤理论的损伤因子定义为:
(3)
式中:D为混凝土受拉或者受压损伤因子;W0为外力在混凝土无损状态下作的功;Wpe为在应变ε时外力作的功,包含可恢复的弹性应变能WP和不可恢复的塑性应变能WE。
结合现行规范对构件破坏程度的描述,建立了各个性能水平的量化标准,具体见表1。

表1 混凝土损伤性能评价的量化标准
钢筋及预应力筋采用理想弹塑性模型。混凝土和钢材的材料参数如表2、3所示。
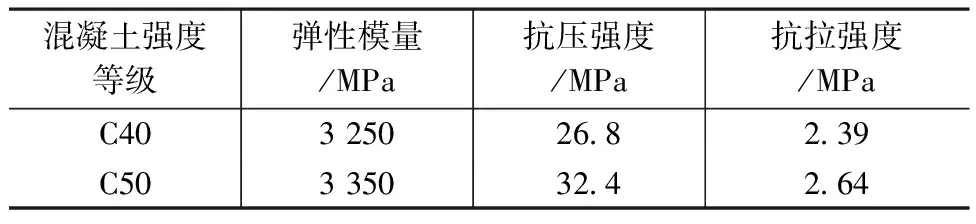
表2 混凝土材料参数
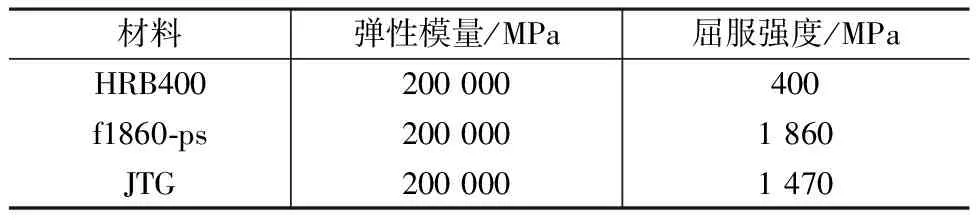
表3 钢筋材料参数
3 计算结果分析
3.1 悬挑端根部设置钢板
原设计模型悬挑端根部未设置钢板,对原模型进行弹塑性分析,其壳底混凝土受压损伤云图见图5。由图发现,在设计荷载(荷载因子为1.3)下悬挑端根部的受压损伤就已经达到0.3,发生中度损坏。针对弹塑性分析结果,对原模型悬挑端根部加强,增设20mm钢板进行弹塑性分析,增加钢板后壳底混凝土受压损伤云图见图6。由图发现,增设钢板后,设计荷载(荷载因子为1.3)下悬挑端根部局部受压损伤为0.1,基本未发生损坏。

图5 原模型壳底混凝土受压损伤云图

图6 增加钢板后壳底混凝土受压损伤云图
3.2 承载力分析
对于结构极限承载力的判断,通常当结构荷载位移曲线达到极值点并出现下降段时,取该极值点为结构的极限承载力。而对于采用荷载控制加载的情况,往往不会出现下降段,此时对于极限承载力的判断需采用迭代求解的方法:当结构维持在某一荷载水平下,结构变形不会持续增加时,认为结构的极限承载力高于这一荷载水平;而当结构维持在某一荷载水平下,结构变形持续增加,则认为该结构的极限承载力低于或等于这一荷载水平[10]。
由于混凝土壳体主要受自重及屋面恒活荷载,为直观反映混凝土壳体的极限承载力水平,定义荷载因子n为混凝土壳体承载力与壳体所承受荷载的比值。混凝土壳体的荷载-位移曲线如图7所示。
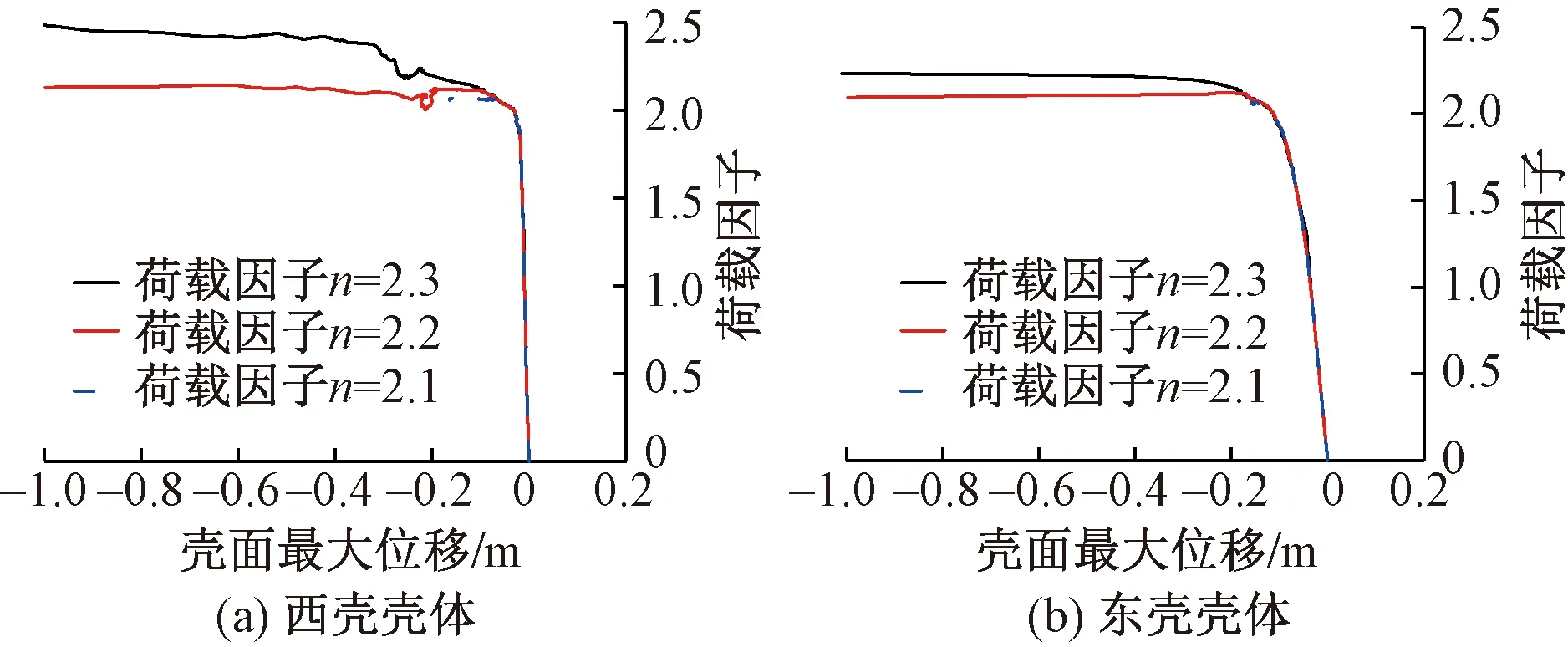
图7 混凝土壳面荷载-位移曲线
由图7可知,该壳体结构的极限承载力对应的荷载因子可偏于安全地取n=2.1。
关于混凝土壳体的极限承载力,我国规范中尚无明确规定。《钢筋混凝土薄壳结构设计规程》(JGJ 22—2012)中仅给出了双曲扁壳在法向荷载下的稳定验算公式。《空间网格结构技术规程》(JGJ 7—2010)[11]给出了网壳结构的极限承载力安全系数,网壳稳定容许承载力(荷载取标准值)应等于网壳稳定极限承载力除以安全系数K;当按弹塑性全过程分析时,安全系数K可取2.0。
当荷载因子大于2时,即混凝土壳体稳定容许承载力大于壳体所承担的荷载,结构的极限承载力满足规范要求。
3.3 混凝土壳的破坏形态及损伤发展全过程分析
极限荷载作用下,大跨混凝土壳体的混凝土受压损伤分布云图、钢筋塑性应变分布云图见图8、9。由图8、9可得,大跨混凝土壳体破坏模式为东壳发生整体失稳破坏,东壳中部区域竖向变形急剧增加,损伤发展严重。由图8可得,壳体底部混凝土受压损伤主要分布在悬挑区、壳体与环梁交界处以及核心筒周边;该区域均为负弯矩区,壳底受压。而壳体顶部混凝土受压损伤主要分布区域为悬挑区和东壳中部,悬挑区顶部混凝土受压损伤主要分布在悬挑梁之间的正弯矩区。
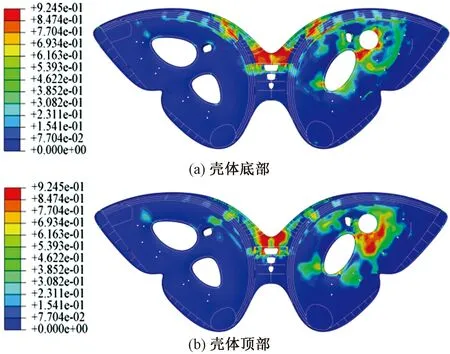
图8 混凝土受压损伤分布云图
由图9可得,东壳上部和中部区域底部钢筋出现较大塑性应变;悬挑区根部顶筋出现较大塑性应变。从中可以看出,东壳中部大片区域发生整体破坏,上部区域发生局部损坏。
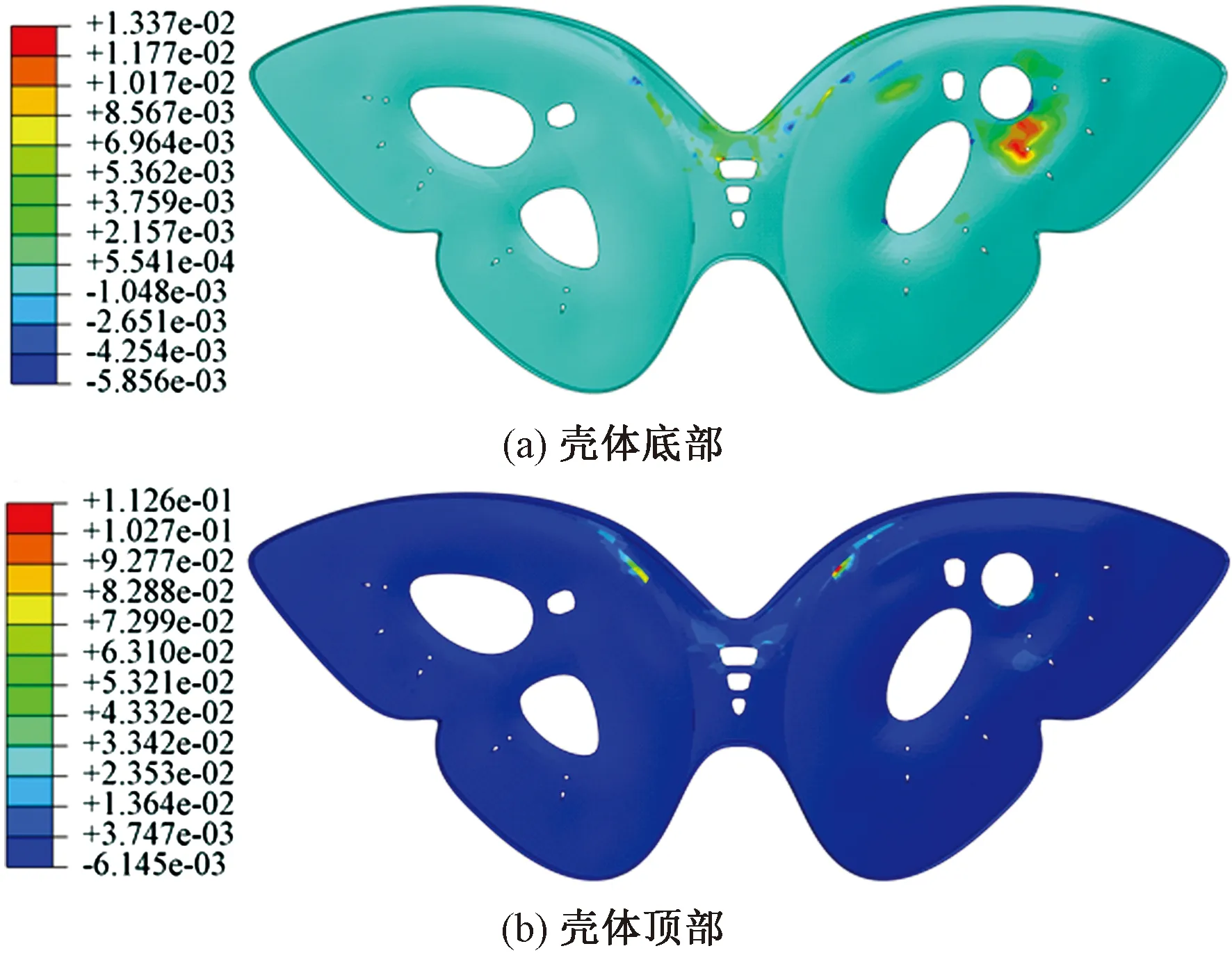
图9 钢筋塑性应变分布云图
混凝土壳面受压损伤发展的全过程分析见图10(图中灰色区域表示受压损伤大于0.5,即混凝土损坏较为严重)。由图可以发现,悬挑区混凝土最先发生破坏,悬挑区增加钢板后混凝土受压损伤未延伸至环梁底部,此时环梁仅柱间区域出现损伤。随着损伤的进一步发展,环梁柱间区域发生破坏,此时悬挑区混凝土已出现大面积损伤,壳面洞边部分出现较大损伤。最终壳面中部区域发生破坏,变形和损伤急剧发展,同时混凝土环梁也出现了多处破坏。

图10 混凝土壳面受压损伤发展全过程
4 极限承载力的影响参数分析
根据经典的线弹性屈曲理论,理想球面壳体在均匀外压作用下的临界荷载Pcr公式为:
(4)
式中:E为壳体材料的弹性模量;R为壳的曲率半径;t为壳的厚度;v为壳体材料的泊松比。
由上式可知,对于弹性理想球面,壳体材料、壳体的曲率半径和壳体厚度对其极限承载力有影响;其中壳体混凝土强度等级和极限承载力成线性关系,曲率半径和壳体厚度与极限承载力成二次幂关系。
异形壳体的弹塑性极限承载力的影响参数较多,包括矢高、材料、厚度、支承条件、预应力大小等。故参考理想球面的弹性承载力公式,选取矢跨比、混凝土强度等级、壳体厚度、预应力大小以及配筋率五个参数,以上述模型为参照模型分别将这五个参数增加20%和减少20%进行比较,分析其对结构极限承载力的影响,具体参数见表4。
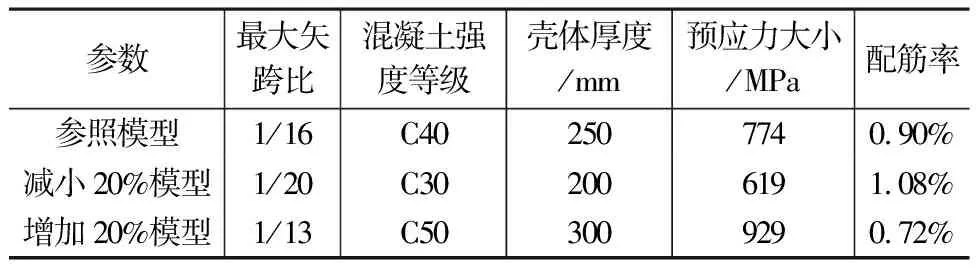
表4 壳体极限承载力影响参数
图11为参照模型矢跨比示意图,图12~16为矢跨比、混凝土强度等级、壳体厚度、预应力大小以及配筋率五个参数对壳体极限承载力的影响曲线。表5为壳体极限承载力参数分析结果。由于该结构的壳体并非理想球面壳体且其矢跨比较小,从壳体结构极限承载力的参数分析结果(图12~16及表5)可以发现,矢跨比对结构极限承载力的影响相对较大,但也远小于式(4)的二次幂关系。而混凝土强度等级、壳体厚度、预应力大小以及配筋率对极限承载力的影响均不太明显,极限承载力的变化率小于10%。其中配筋率对极限承载力的影响几乎没有,这是因为壳体发生的是屈曲失稳破坏,与配筋率的关系较小。
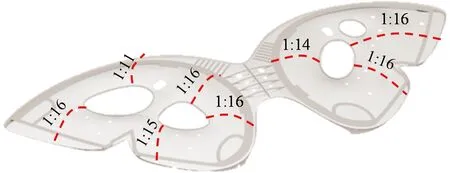
图11 参照模型矢跨比示意图[3]
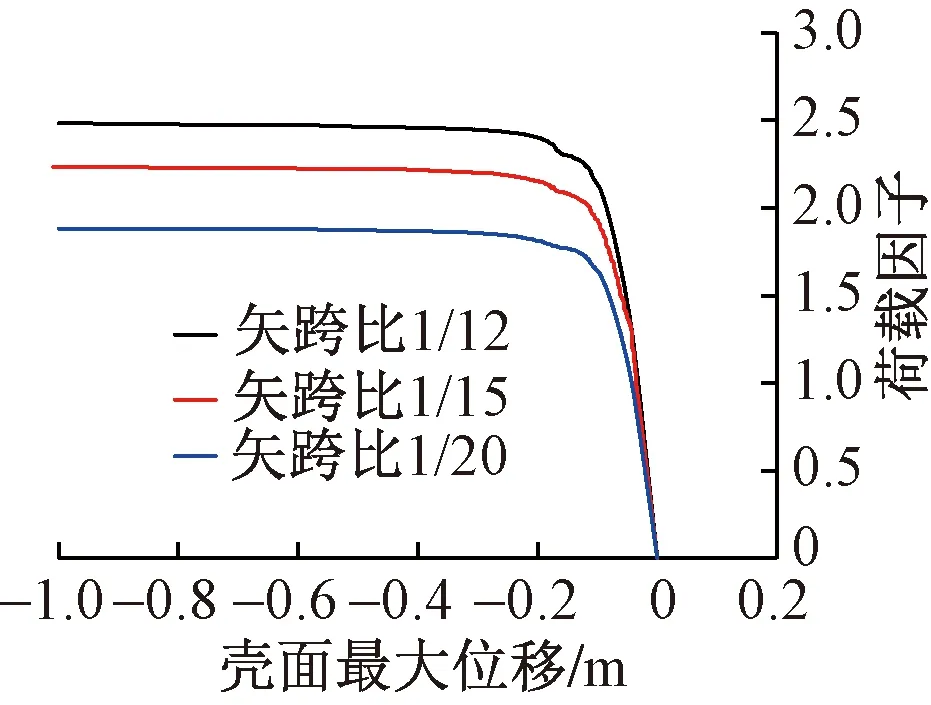
图12 矢跨比对极限承载力的影响
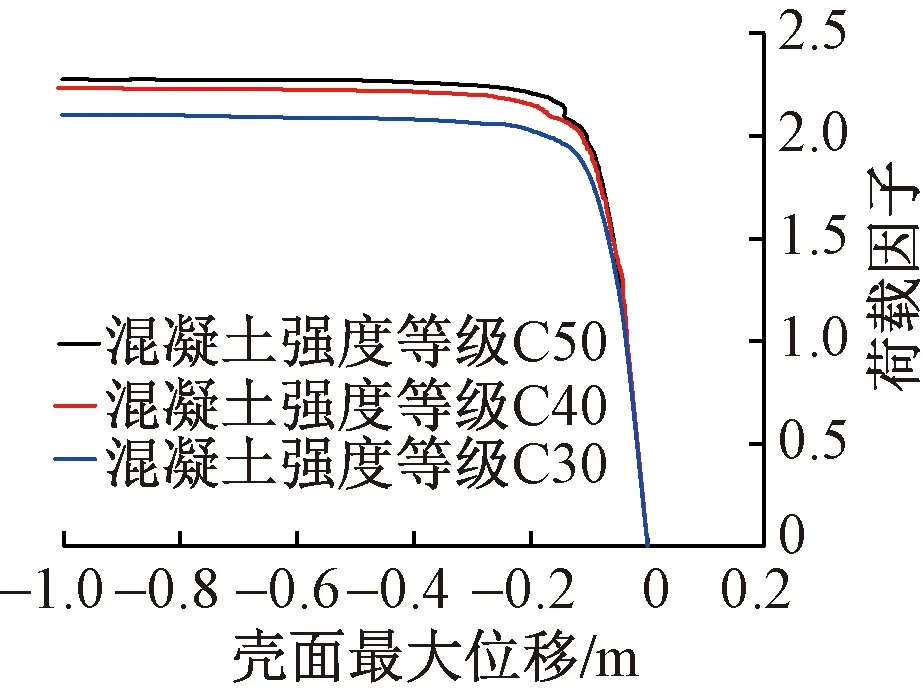
图13 混凝土强度等级对极限承载力的影响
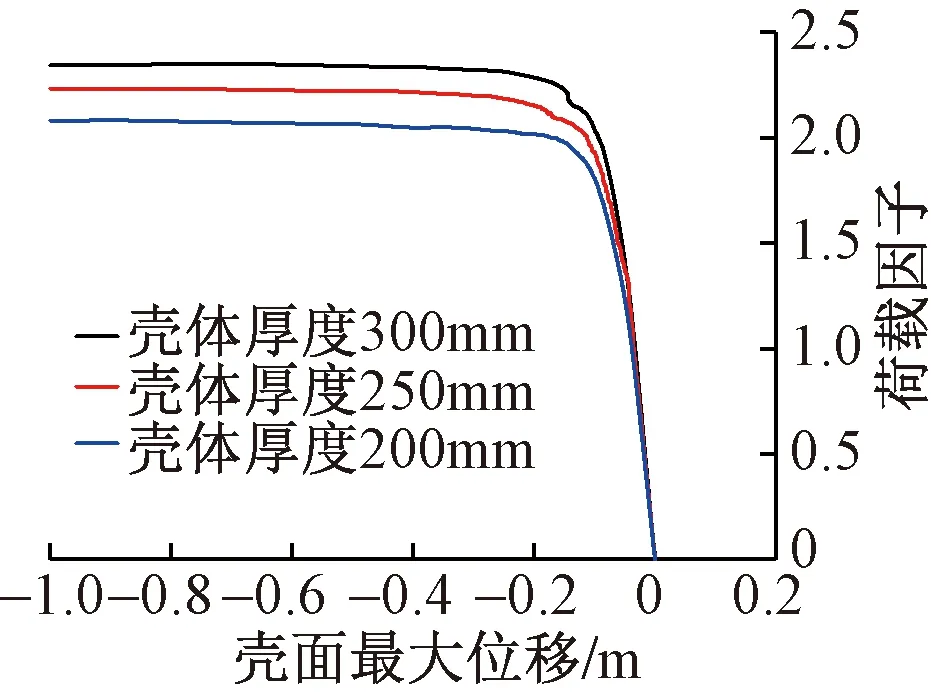
图14 壳体厚度对极限承载力的影响
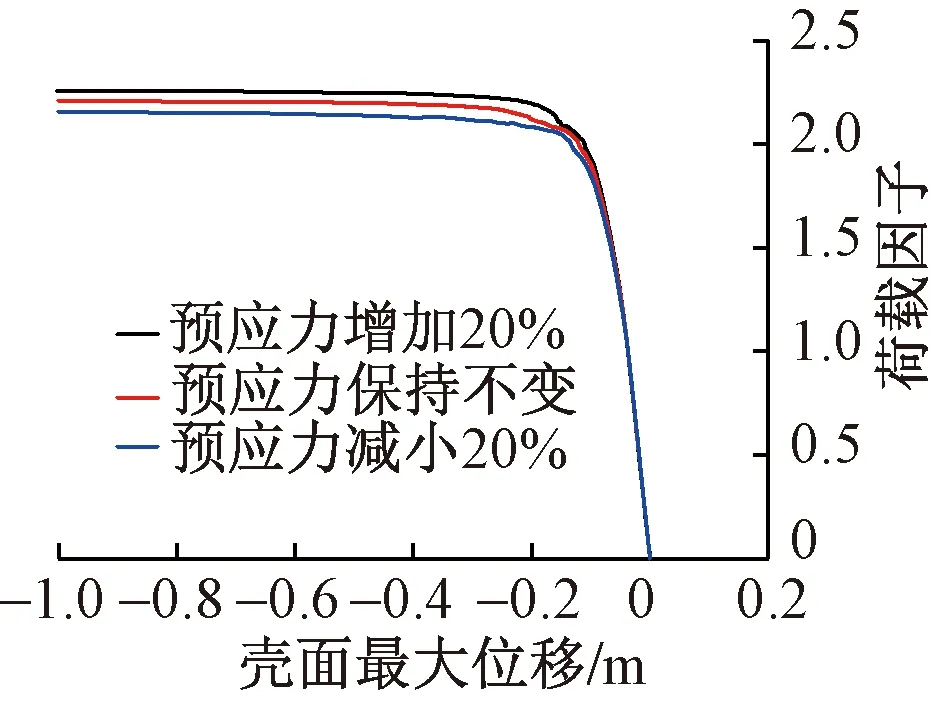
图15 预应力大小对极限承载力的影响
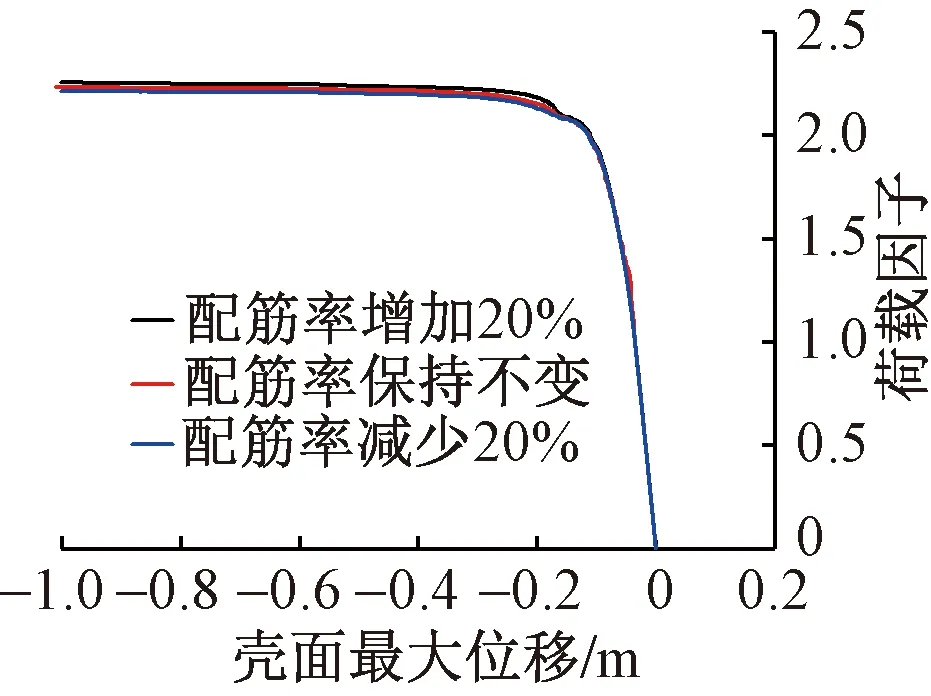
图16 配筋率对极限承载力的影响
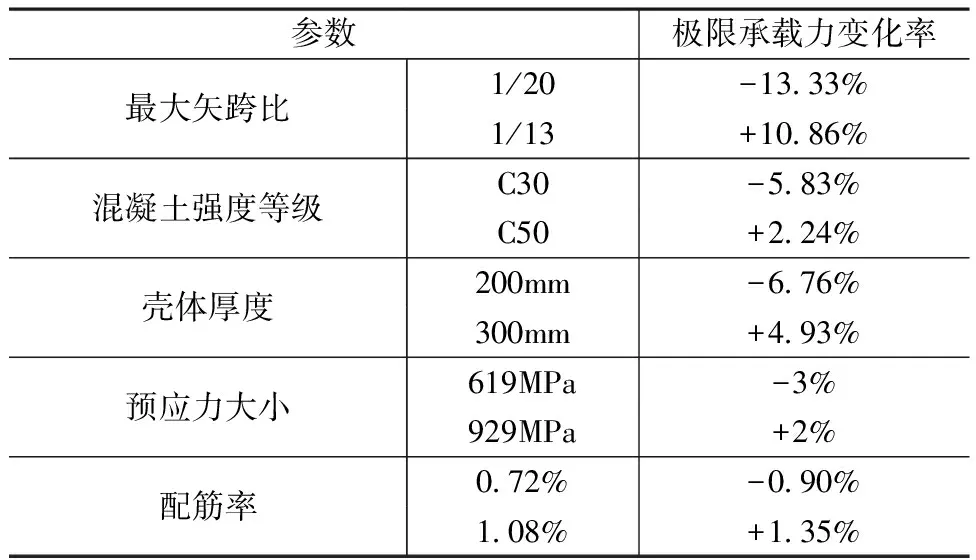
表5 壳体极限承载力参数分析结果
通过对结构极限承载力的参数分析,可以大体了解各设计参数对该壳体结构极限承载力的影响规律,从而使得设计参数的选取更加具有安全性与经济性。本工程壳体的矢跨比就是结合建筑造型与结构极限承载力确定的。
5 结论
(1)壳体结构的极限承载力能满足规范要求。破坏模式为东壳的整体失稳破坏,极限荷载下壳面混凝土受压损伤主要集中在悬挑区和东侧壳面中部区域。壳面破坏过程为悬挑区先发生破坏,进而柱间混凝土产生较大的受压损伤,最终东侧壳面中部区域发生失稳破坏。
(2)采用隐式动力算法对结构进行拟静力分析,该方法不存在显示动力算法的累积误差问题,具有较高的精度及良好的收敛性,从分析结果看也符合结构受力的概念判断。
(3)矢跨比对结构极限承载力的影响相对较大,而混凝土强度等级、壳体厚度、预应力大小以及配筋率对极限承载力的影响均不明显。其中配筋率对极限承载力的影响几乎没有。
(4)可以利用弹塑性分析结果对结构性能进行评估并指导结构设计。采用在悬挑端根部增加型钢后,设计荷载下混凝土损伤大幅降低,壳体基本完好。通过对结构极限承载力的参数分析,结合建筑外形确定矢跨比。

