第十届中国花卉博览会世纪馆大跨度旋转楼梯结构设计与分析

杨成栋, 黄永强,2, 闫泽升, 黄燕平

(1 华建集团华东建筑设计研究院有限公司，上海 200002；2 上海超高层建筑设计工程技术研究中心，上海 200002；3 隔而固(青岛)结构设计事务所有限公司，青岛 266100)

1 工程概况

第十届中国花卉博览会世纪馆[1]屋盖是高度约15m的混凝土薄壳结构,屋面为屋顶花园。在中央天井有一座3层旋转楼梯直通混凝土壳面。该楼梯总高度11.2m,累计旋转角度1 080°,建筑形式如图1所示。

由于旋转楼梯每层直径均不一致,1层直径10.75m,2层直径12.75m,3层直径8.75m。且为了建筑效果的美观和轻盈,仅在内圈一侧设立1根立柱,为旋转楼梯提供部分竖向刚度,结构最大悬挑尺寸为9.8m(从立柱中心至旋转楼梯最外侧)。为了减小外梯梁的结构高度,在楼梯断面上采用单边悬挑的结构形式。

2 旋转楼梯结构设计

本工程楼梯采用的是单边悬挑的形式,则楼梯的主要刚度由内梯梁提供。内梯梁采用钢箱梁,截面尺寸为700×300×20×20,而外梯梁则采用截面尺寸为200×200×10×10的钢箱梁,外梯梁主要起到拉结作用。内、外梯梁之间采用变截面的H型钢梁连接。

为减小旋转楼梯竖向变形,在楼梯内侧设置1根钢柱,将3层楼梯连接起来。然而由于柱顶无法支撑在壳顶边缘,会在柱底产生较大弯矩,故采用柱底铰接的形式以减小柱截面尺寸,钢柱截面为φ325×30。钢柱与内梯梁采用销轴连接。

2.1 计算模型

由于旋转楼梯是一个空间螺旋结构,本工程通过Rhino模型提取杆件轴线,再导入SAP2000进行设计和分析。钢梁、钢柱均采用杆单元进行模拟,旋转楼梯计算模型如图2所示。楼梯活荷载取3.5kN/m2,对旋转楼梯的承载能力极限状态和正常使用极限状态的荷载组合分别按《建筑结构荷载规范》(GB 50009—2012)[2]规定的基本组合和标准组合进行考虑。

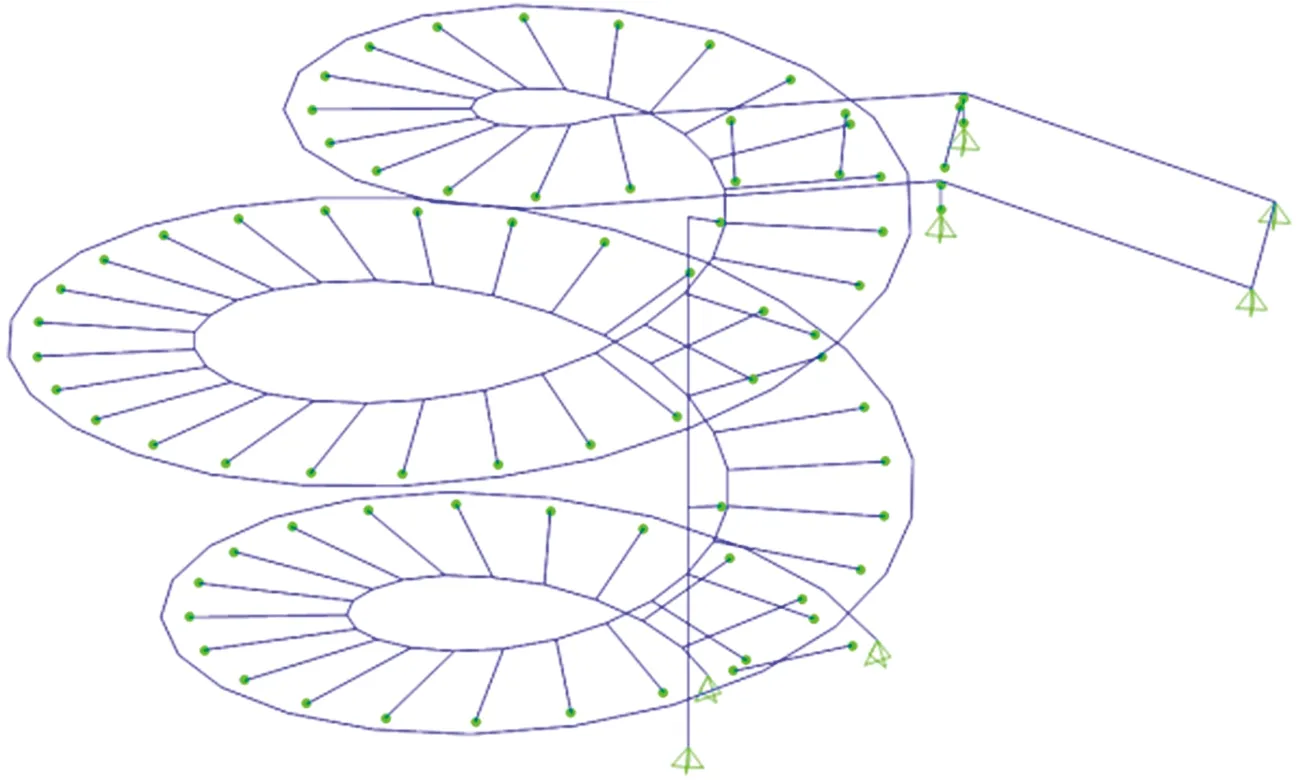
图2 SAP2000计算模型

2.2 静力计算结果

2.2.1 结构周期与振型

对旋转楼梯进行模态分析,结构前三阶振型如图3所示。旋转楼梯自振周期及质量参与系数见表1。从图3及表1中可以看出,由于结构的空间螺旋特性,X、Y、Z三个方向的质量参与系数均小于0.5,并没有明显的平动振型。

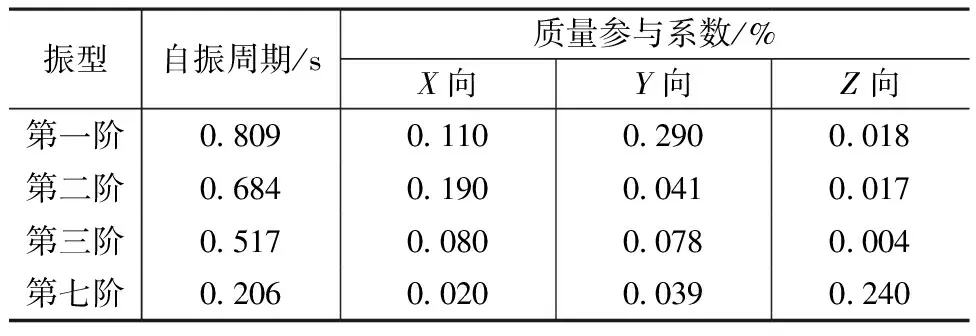
表1 旋转楼梯自振周期及质量参与系数

图3 旋转楼梯前三阶振型图

2.2.2 结构强度与变形

对旋转楼梯不同边界条件支座采用以下4种模型进行对比分析,以确定柱底、梯梁端部以及钢柱与梯梁的连接形式。模型一(铰接模型):柱底、梯梁端部以及柱与梯梁的连接均采用铰接连接,见图2。模型二(柱底刚接模型):柱底采用刚接,梯梁端部以及柱与梯梁的连接采用铰接,见图4(a)。模型三(柱与梯梁刚接模型):柱底和梯梁端部采用铰接,柱与梯梁采用刚接连接,见图4(b)。模型四(梯梁底部刚接模型):梯梁端部采用刚接,柱底以及柱与梯梁采用铰接模型,见图4(c)。

图4 不同边界条件的计算模型

不同边界条件的模型计算结果如表2所示。从表中可以看出,柱底刚接(模型二)对竖向位移改善较大,但钢梁和钢柱应力比均增大。铰接模型(模型一)的钢梁应力比最低,只有0.381;而竖向位移和钢柱应力比未显著增大,并且铰接模型传力简单明确。因此最终采用铰接模型进行旋转楼梯的分析与设计。

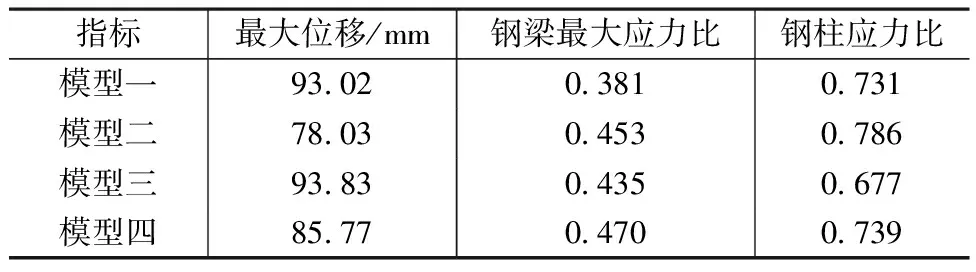
表2 不同边界条件模型计算结果对比

2.3 弧形梯梁的强度及稳定计算

2.3.1 弧形梯梁的强度校核

由于《钢结构设计标准》(GB 50017—2017)[3](简称钢标)中没有钢梁在扭矩下的相关计算规定,而螺旋楼梯梯梁受扭的问题却无法避免。故本文采用基于第四强度理论的复合应力公式进行承载能力校核,即钢标中式(6.1.5-1),见式(1)。

(1)

式中:σc为局部压应力,取为0;β1为强度增大系数,取1.1;f为钢材强度设计值;σ为正应力;τ为剪应力。

提取梯梁截面在弯矩最大、扭矩最大、剪力最大以及轴力最大工况下的梯梁内力(表3),并分别进行考虑扭矩的承载能力校核。

表3 不同工况的梯梁内力

以扭矩最大工况为例进行强度计算。

(1)扭矩作用下的剪应力计算

钢梁在扭矩作用下通常都发生约束扭转,可根据薄壁杆件的约束扭转理论进行计算。由于薄壁箱形钢梁在扭矩作用下存在翘曲、畸变和剪切滞后效应,约束扭转的理论研究多采用扇形坐标和双力矩法,求解过程相当繁琐[4-7]。并且箱形截面约束扭转下的翘曲正应力通常比较小,因此本文仅按自由扭转考虑扭矩作用下钢梁的剪应力τT为:

式中:A为截面面积;t为截面壁厚。

剪力作用下的钢梁2、3轴剪应力τ2、τ3为:

式中:S2、S3分别为2、3轴的截面静矩;I2、I3分别为2、3轴的截面惯性矩。

轴力和弯矩作用下的钢梁正应力σ为:

式中y2、y3分别为2、3轴计算点距惯性轴的距离。

按第三强度理论计算的折算应力比为:

(2)

从式(2)可以看出,构件承载力满足规范要求。

表4为不同目标工况下的梯梁应力比。从表4可以看出,扭矩最大工况为梯梁的控制工况,考虑扭矩时的钢梁应力比为0.439,要远大于不考虑扭矩时的钢梁应力比,最大相差约40%。因此对于旋转楼梯的梯梁设计,考虑扭矩的影响是必要的。

表4 不同目标工况下的梯梁应力比

2.3.2 弧形梯梁的局部稳定分析

钢标对于实腹式受弯构件和压弯构件的局部稳定是通过腹板和翼缘的宽厚比来控制。当板件宽厚比不满足要求时,需设置加劲肋或者按考虑屈曲后强度进行设计。

然而由于旋转楼梯梯梁的受力复杂,对于钢梁在扭矩下的局部稳定是否需要计算以及如何计算,钢标并无相关说明。因此本文采用钢标受弯构件的局部稳定计算方法对箱形梯梁在扭矩作用下的局部稳定进行验算。

以扭矩最大工况为例,按钢标式(6.3.3-1)计算弧形梯梁局部稳定:

(3)

式中字符含义见钢标。

从上述分析可以看出,箱形截面梯梁在考虑扭矩的情况下,梯梁局部稳定应力比小于规范限值1,满足要求。并且对比局部稳定计算式(3)和承载力计算式(2)可以发现,局部稳定的应力比计算采用的是平方项,应力水平的影响相对较小,主要由板件宽厚比控制。

2.4 极限承载力分析

采用SAP2000软件对旋转楼梯进行弹性整体屈曲分析和弹塑性极限承载力分析。

2.4.1 弹性整体屈曲分析

旋转楼梯在标准荷载组合(1.0D+1.0L)(D为恒载,L为活载)下的前三阶整体屈曲因子见表5,其中第一阶屈曲模态见图5。

表5 旋转楼梯前三阶屈曲因子

图5 旋转楼梯前三阶屈曲因子

从表5中可以看出,旋转楼梯整体屈曲分析的屈曲因子为5.77,即当荷载达到5.77(D+L)时,旋转楼梯发生失稳破坏,破坏模式为立柱失稳破坏。

2.4.2 弹塑性极限承载力分析

进一步对旋转楼梯进行考虑几何非线性和材料非线性的弹塑性时程分析。在梯梁和立柱弯矩较大处设置塑性铰,位置如图6所示。

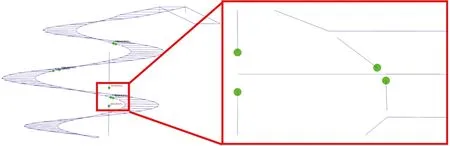
图6 塑性铰布置示意图

图7为旋转楼梯荷载因子-竖向位移曲线。由图可见,塑性铰首次出现在立柱中部与梯梁连接处,此时旋转楼梯弹塑性整体屈曲的极限荷载为3.50(D+L)。

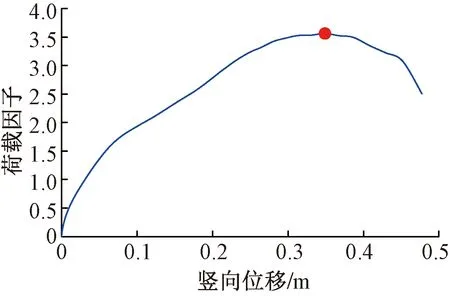
图7 杆元模型荷载因子-竖向位移曲线

对比弹性和弹塑性极限承载力分析,分析结果均为立柱的屈曲破坏。而弹性分析时立柱的应力比为0.731,对应荷载为1.3D+1.5L,换算成立柱刚屈服时的荷载因子n为:

式中:fy为钢材屈服强度;Wp为截面塑性模量;Wn为净截面模量;γm为截面塑性发展系数。

旋转楼梯的极限承载力计算可参考《空间网格结构技术规程》(JGJ 7—2010)[8]:网壳稳定容许承载力(荷载取标准值)应等于网壳稳定极限承载力除以安全系数K。当按弹塑性全过程分析时,安全系数K可取2.0;当按弹性全过程分析时,安全系数K可取4.2。

弹性计算的荷载因子为5.77>4.2,弹塑性计算的荷载因子为3.5>2。结果表明,旋转楼梯的极限承载力能满足《空间网格结构技术规程》(JGJ 7—2010)的要求。

3 旋转楼梯舒适度计算

《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441—2019)[9]4.2.4节中连廊和室内天桥的第一阶横向自振频率不宜小于1.2Hz。连廊和室内天桥的振动峰值加速度不应大于表6的限值。

表6 连廊和室内天桥的振动峰值加速度限值/(m/s2)

旋转楼梯宜采用不封闭连廊,根据表6,本项目竖向加速度限值取0.05g(0.50m/s2)。

3.1 人致荷载激励模型

《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441—2019)第5.2节规定,人行激励荷载可按下式计算:

这种基于学校整体资源的实验班设置模式具有独特的优势。首先，实验班不区分专业，只按照文理进行招生，招生规模大；其次，由于学生自主选课，可以充分发挥学科齐全、教学资源优良的优势；第三，学生不受限于某一学科强调全面发展；第四，学生自主性最大化，学生拥有独立的选择；第五，学制安排灵活，学生可以根据个人情况自主变换课程安排，完成学分要求即可毕业;第六，导师指导学习计划的指定和实施，给予学生最直接的帮助。

表7 人行荷载激励的动力因子和相位角

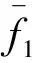
(4)

式中n为整数,可取1、2、3。

3.2 结构动力响应

分析计算过程中,将人行激励以均布荷载的形式施加于旋转楼梯,鉴于文章篇幅有限,在此仅列出敏感节点28和节点78的振动响应,位置见图8。敏感节点的竖向振动加速度响应见图9。从图9中可以看出,楼梯敏感位置节点竖向振动不满足舒适度要求,需要采取减振措施。

图8 旋转楼梯敏感节点

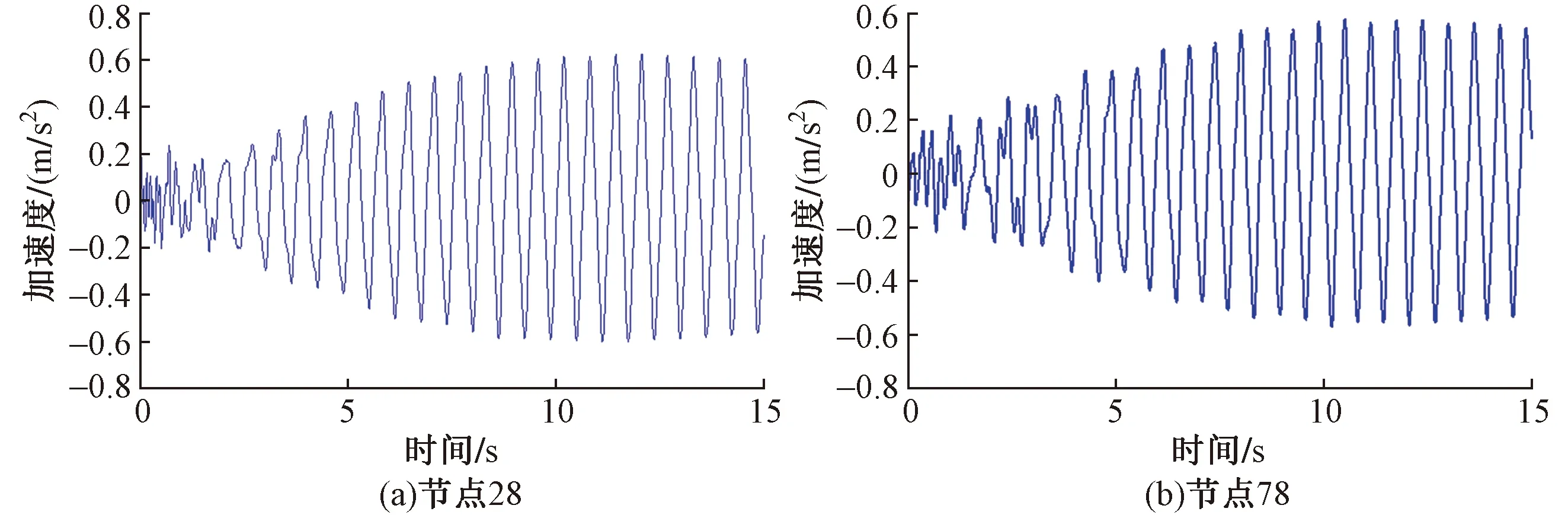
图9 敏感节点的竖向振动加速度响应

3.3 采用TMD的减振分析

根据楼梯的动力固有特性和人行激励下竖向加速度振动响应情况,沿旋转楼梯共布置了8个TMD,TMD分别布置在结构振动较大位置,见图10。

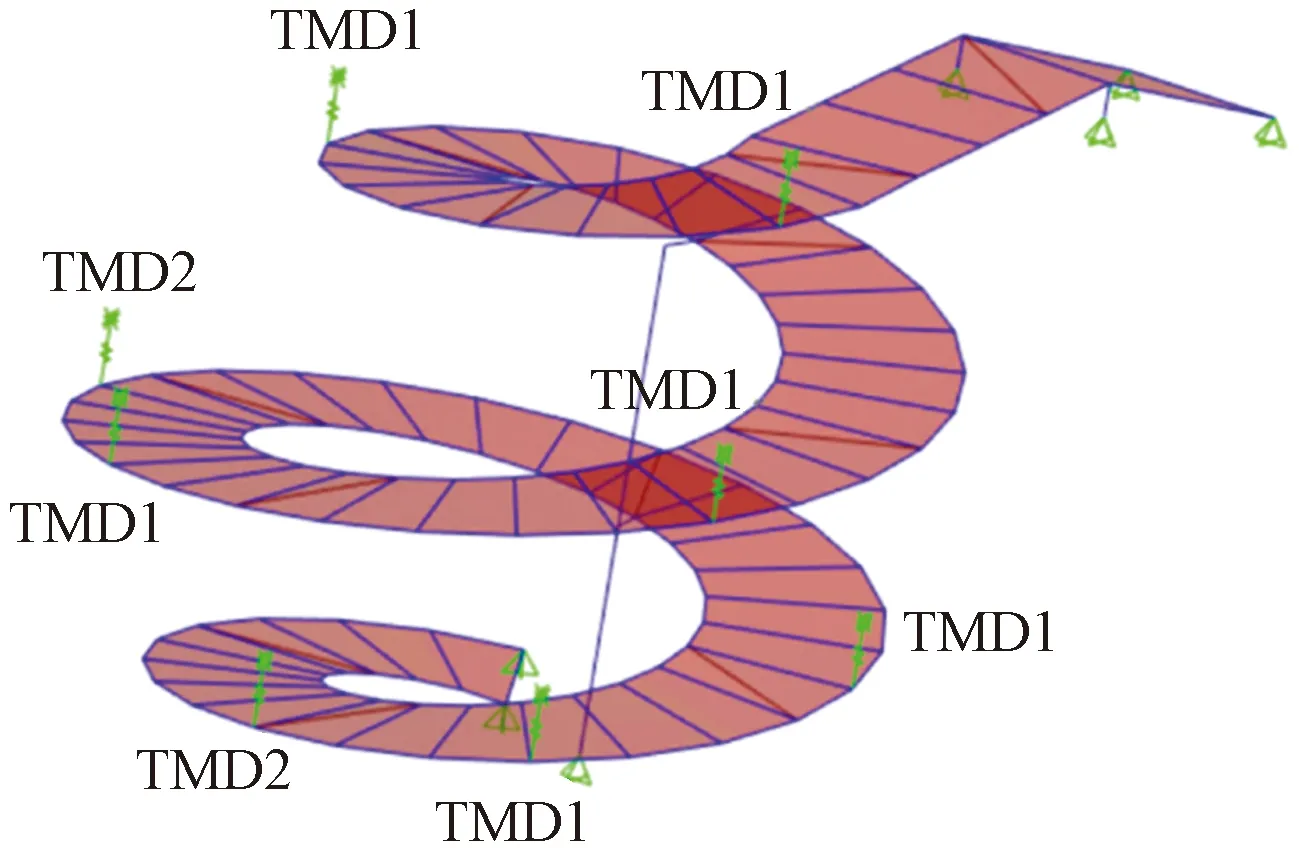
图10 TMD布置示意图

TMD的设计参数如表8所示。

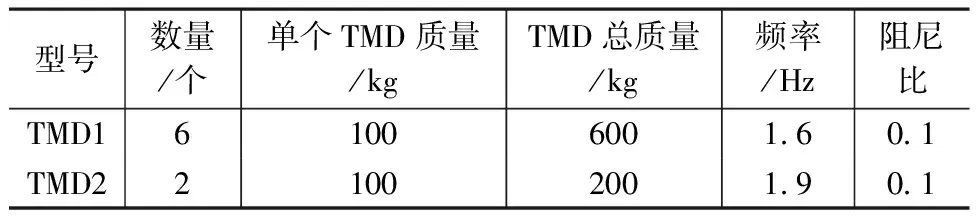
表8 TMD的设计参数

图11为旋转楼梯安装TMD前后节点28和节点78的竖向振动加速度响应。从图中可以看出,安装TMD后,结构的振动有明显减弱的趋势,减振效果见表9。

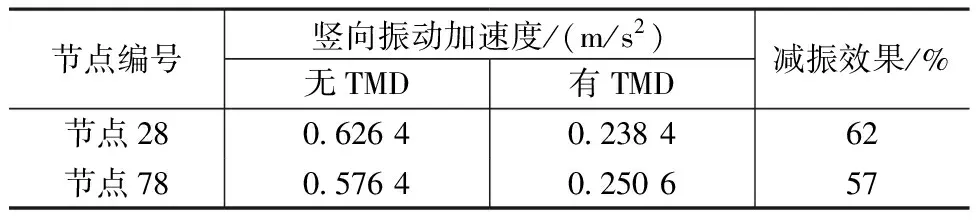
表9 旋转楼梯安装TMD前后竖向振动加速度对比

图11 安装TMD前后敏感节点的竖向加速度响应

旋转楼梯在安装0.8t的TMD后,在人行荷载激励下的振竖向动加速度峰值有很大程度的降低,满足《建筑楼盖结构振动舒适度技术标准》(JGJ/T 441—2019)的加速度限值要求。

4 有限元分析

4.1 有限元模型

采用ABAQUS对旋转楼梯进行弹塑性分析,有限元模型中梯梁和踏步板采用壳单元模拟,立柱和平台梁采用杆单元模拟,分析模型采用隐式分析[10]。对旋转楼梯采用壳元模型进行有限元分析,如图12所示。并与SAP2000杆元模型分析结果进行对比,以验证杆元简化模型的正确性。分别采用如下三种工况对比壳元模型与杆元模型在应力比、位移以及极限承载力方面的差异。工况1:基本组合1.3D+1.5L;工况2:标准组合1.0D+1.0L;工况3极限状态,N(D+L),其中,N为极限状态的荷载因子。

图12 旋转楼梯有限元模型

4.2 计算结果对比

工况1下梯梁应力分布云图见图13。由图可得,工况1下梯梁最大应力为228MPa,位于与立柱连接处,经计算,最大应力比为0.773,远大于杆元模型计算的钢梁应力比,这是因为采用壳元模型分析时会存在局部应力集中的现象。从图13中可以看出,内梯梁除应力集中处外的应力约为130～150MPa,应力比为0.440～0.508,与2.3.1节按考虑扭矩计算得到的钢梁最大应力比0.439非常接近,表明了按简化方法考虑扭矩影响的可行性。

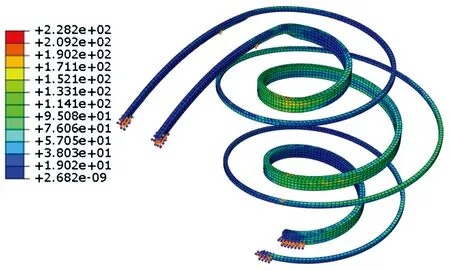
图13 工况1下梯梁应力分布云图/MPa

工况2下旋转楼梯的竖向位移分布如图14所示。由图可以看出,旋转楼梯最大位移为108mm,SAP2000杆元模型计算的标准组合下结构最大位移为93mm,两者差异不大,表明了对旋转楼梯采用杆元模型进行计算的可行性和合理性。

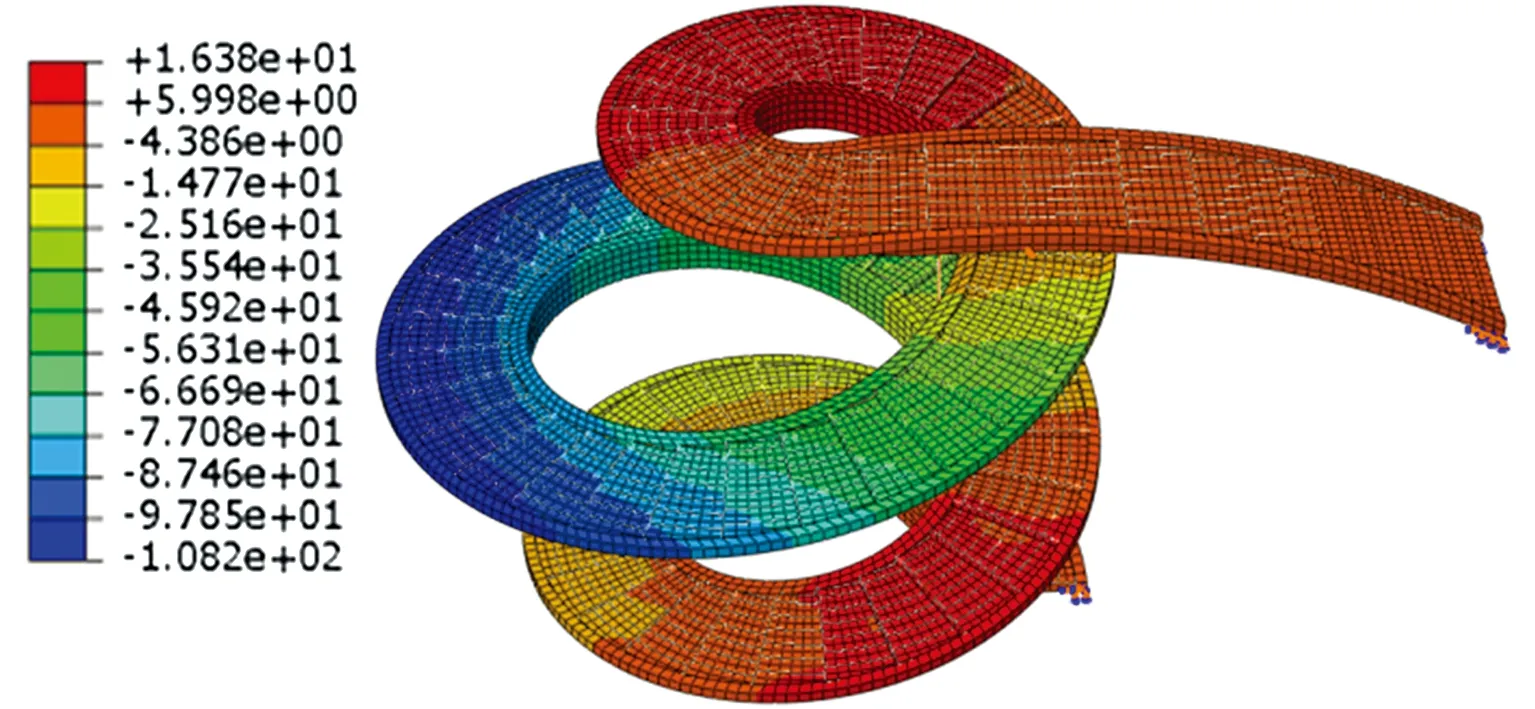
图14 工况2下旋转楼梯竖向位移分布云图/mm

工况3下旋转楼梯的荷载因子-竖向位移曲线见图15。由图可得,旋转楼梯弹塑性分析的安全系数为4.28。壳元模型因为考虑了踏步板的整体作用,其计算得到的极限承载力要大于按杆元模型计算得到的极限承载力。

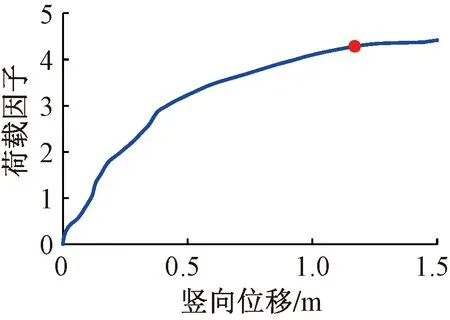
图15 壳元模型荷载因子-竖向位移曲线

5 旋转楼梯连接节点设计

旋转楼梯梯梁与钢柱的连接均采用销轴连接,如图16、17所示。采用销轴节点不仅简洁、美观,而且传力明确。

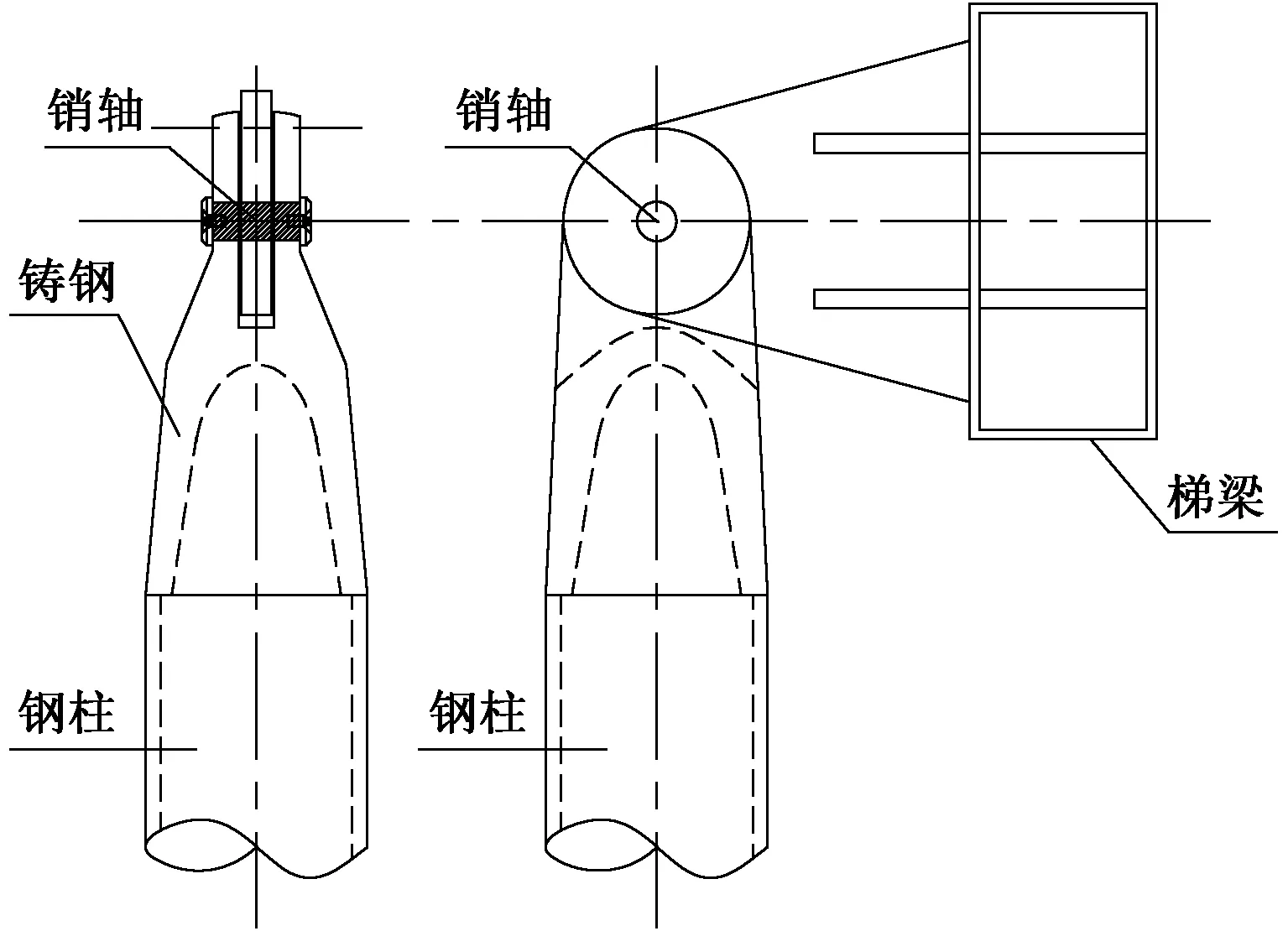
图16 梯梁与柱顶销轴连接节点

图17 梯梁与柱中销轴连接节点

柱底采用铸钢铰接节点,可以减小节点区的焊接次应力对结构设计的影响,并且柱底采用球形连接更加符合铰接节点的设计,如图18所示。

图18 柱底铰接节点

6 结论

(1)比较不同支座边界条件对旋转楼梯竖向位移和杆件应力比的影响,确定了按传力简单明确的铰接模型进行设计。与不考虑扭矩影响的旋转楼梯构件应力比相比,考虑扭矩影响的应力比增加约40%。旋转楼梯梯梁的设计不可忽视扭矩的影响,否则将存在较大的安全隐患。

(2)对旋转楼梯分别进行弹性和弹塑性屈曲分析,结果表明旋转楼梯的极限承载力均能满足规范要求。

(3)本文对旋转楼梯进行了舒适度分析,分析结果表明,楼梯的人行荷载激励下的竖向振动加速度大于规范限值0.5m/s2,需采用减振措施;旋转楼梯在安装0.8t的TMD后,结构在人行激励下的振动加速度峰值大幅降低,满足规范要求。

(4)对旋转楼梯采用壳元模型进行有限元分析,并与杆元模型进行对比。结果表明采用壳元模型计算的梯梁应力、竖向位移均与杆元模型计算结果接近,表明采用杆元简化模型进行设计分析是可行的。