第十届中国花卉博览会世纪馆变截面铸钢柱脚的设计与研究

罗 遥, 黄永强,2, 闫泽升

(1 华建集团华东建筑设计研究院有限公司，上海 200002；2 上海超高层建筑设计工程技术研究中心，上海 200002)

1 工程概况

世纪馆是第十届中国花卉博览会场馆之一,整体外形犹如展翅的蝴蝶(图1)。世纪馆东西向长度约280m,南北向长度约115m,建筑高度约15m[1]。屋顶为自由曲面预应力混凝土薄壳结构,壳体支撑在剪力墙和长细摇摆柱之上,壳体典型厚度为250mm。

图1 世纪馆现场照片

世纪馆中共设有131根,9种截面的无缝钢管柱(图2),柱子长度为6.1～13.6m,钢管钢材牌号均为Q355B。为满足建筑效果,钢管柱的顶部和底部截面局部收进,可供后期放置灯具。为满足造型及承载能力的需要,柱脚节点采用一体化铸钢节点[2-4],铸钢牌号均为ZG340-550H。典型柱脚、柱顶节点详图如图3所示。

图2 无缝钢管柱现场照片

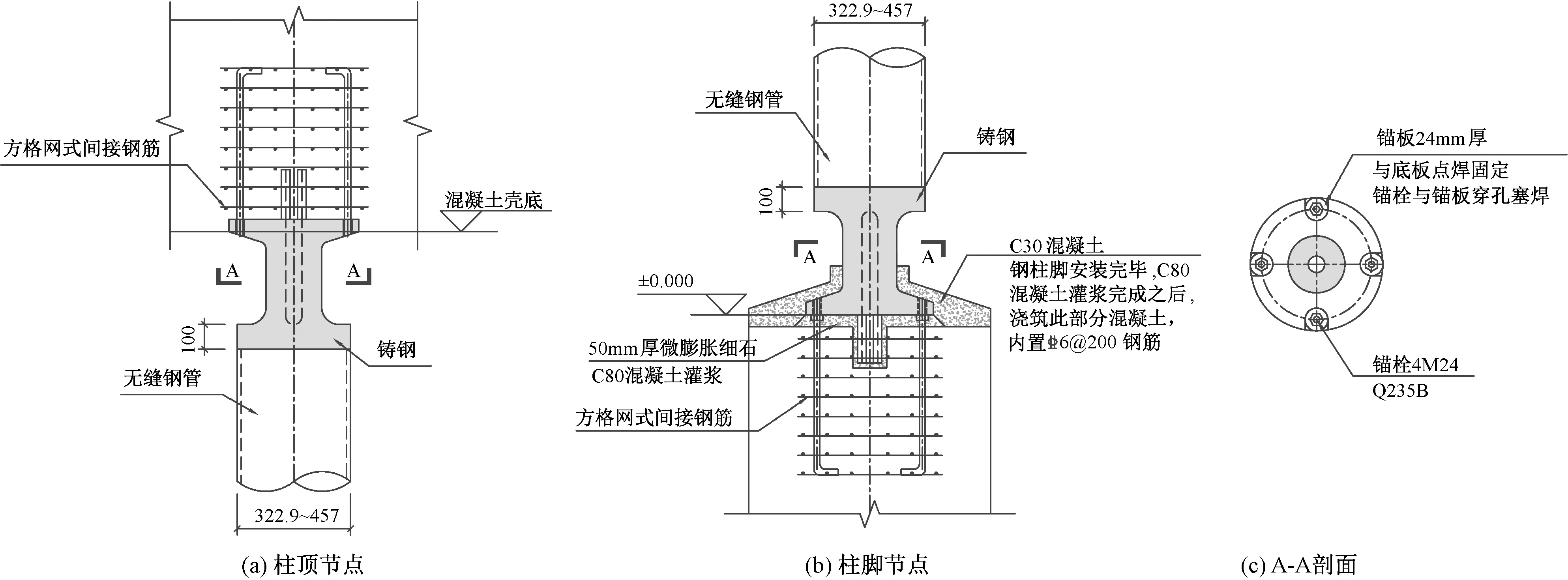
图3 典型柱顶、柱脚节点

针对铸钢柱脚节点(由于柱顶、柱脚节点对称,后文均称柱脚节点),本文首先介绍了设计的过程及难点,然后采用通用有限元软件ABAQUS对其承载能力进行验证,分析柱脚的应力状态,最后对不同截面、轴力及柱高的钢柱模型的抗侧刚度进行分析,提出钢柱的简化模型,为整体模型中钢柱的连接形式提供设计依据。

2 变截面铸钢柱脚的初步设计

根据无缝钢管尺寸,选取3种典型截面,截面参数及轴力如表1所示。设计柱脚过程中,对铸钢件颈部截面、顶部托盘、柱脚底板分别做以下考虑。

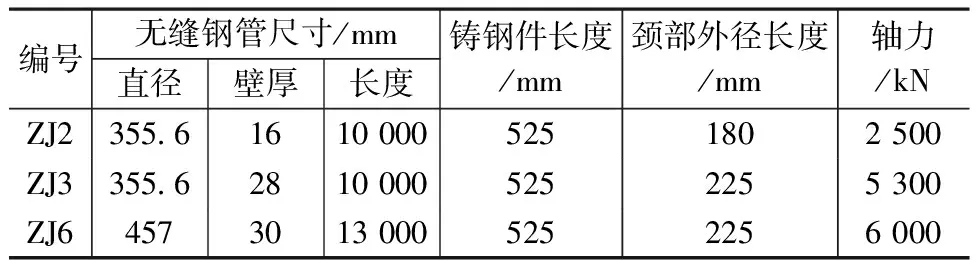
表1 无缝钢管柱尺寸及轴向荷载

2.1 颈部截面

颈部截面的外径尺寸根据建筑需求给出(表1)。根据《铸钢结构技术规程》(JGJ/T 395—2017)[5](简称《铸钢规程》)要求:铸钢壁厚不宜大于150mm,故在铸钢中部设置空腔,铸钢颈部截面为圆环状(图3(c))。颈部截面的壁厚根据其所承担的轴力和弯矩进行设计,见式(1),使其承载力满足《铸钢规程》要求:

N/A+M/γmW≤f

(1)

式中:N、M分别为柱脚轴向压力、弯矩设计值;A、W分别为柱脚颈部截面面积、截面模量;γm为圆形构件的截面塑性发展系数;f为铸钢件抗拉强度设计值。

本项目中柱子长细比较大,柱子均视为摇摆柱进行设计,抗侧承载力由剪力墙提供。但是在实际构造中,柱脚不能做到完全铰接,柱子会分担一定弯矩,故若只考虑摇摆柱受到的轴力进行截面设计,将偏于不安全。若弯矩按钢柱固接确定,在建筑需求的外径尺寸下,截面压弯承载力无法满足《铸钢规程》要求。因此初步设计中,颈部截面壁厚暂按截面在轴力作用下的应力比低于0.6确定,如表2所示。通过有限元对钢柱的抗侧刚度加以分析,明确柱脚连接形式,确定柱脚所受到的弯矩,并对颈部承载力进行校核。

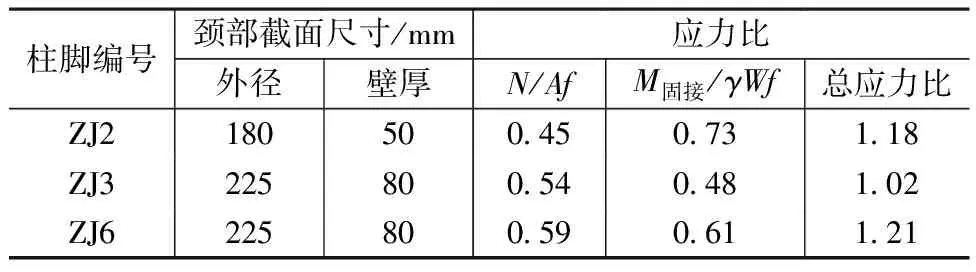
表2 各柱脚铸钢件颈部截面尺寸及应力比

2.2 顶部托盘

铸钢件顶部托盘的直径与无缝钢管相同。顶部托盘的厚度t1按悬臂板进行设计,验算根部截面正应力σ、剪应力τ及正应力和剪应力共同作用下的折算应力是否满足《钢结构设计标准》(GB 50017—2017)[6](简称《钢标》)要求,计算公式见式(2)～(4):

σ=[3N(D-d)]/πdt12≤f

(2)

τ=N/πdt1≤fv

(3)

(4)

式中:D为无缝钢管直径;d为铸钢颈部直径;fv为铸钢件抗剪强度设计值。

如表3所示,根据式(2)～(4)得到各铸钢件顶部托盘所需厚度均较大。由于壁厚的增加,铸钢件的强度、伸长率、冲击功等重要指标均会降低[5],因此在设计中,托盘厚度取100mm,并在托盘与颈部之间设置倒角(图3),以满足厚度需求。

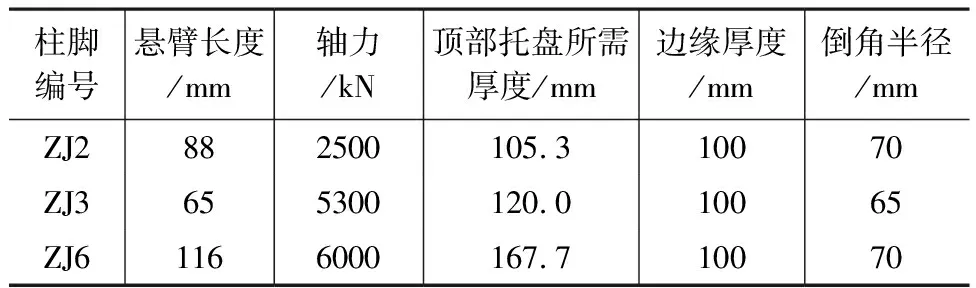
表3 各柱脚铸钢件顶部托盘所需厚度

此外,在设计顶部托盘过程中,考虑如图4的两种构造形式,分别为整体性能更佳的空腔不贯通形式与铸造工艺相对简单的空腔贯通形式。通过后续有限元分析对两者受力性能进行对比。

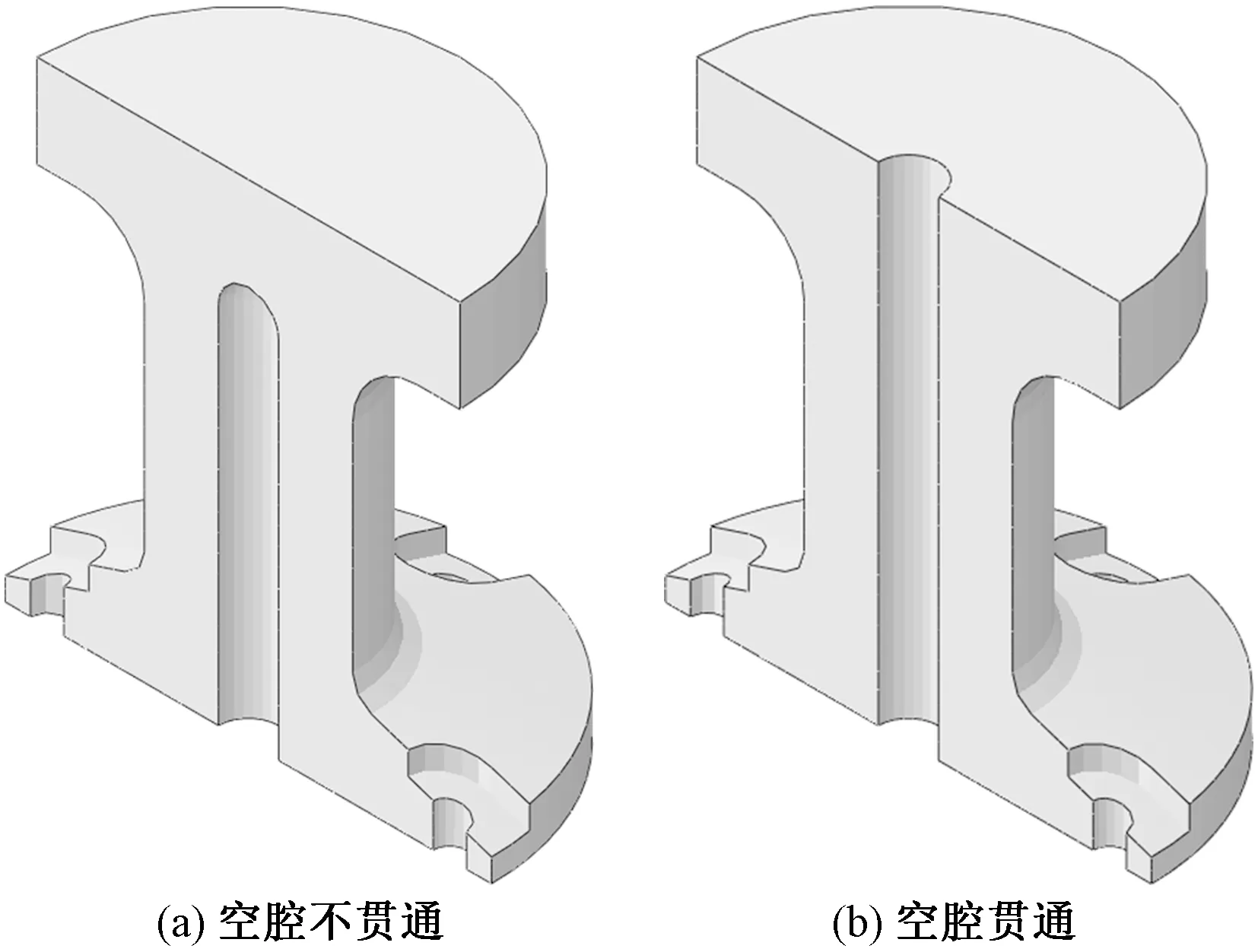
图4 铸钢件顶部托盘两种构造形式

2.3 柱脚底板

柱脚底板的直径D′根据混凝土基础局部受压承载力确定。在混凝土局部受压验算时,局压面积通常按柱脚底板的面积采用。对于本项目中的柱脚,由于铸钢件颈部壁厚较厚,对应位置的混凝土压应力显著高于四周,局部受压面积若仍按柱脚底板面积考虑,可能会高估局压承载力。因此设计时做了如下考虑:1)配置方格网式间接钢筋,柱轴力与局压承载力比值控制在0.6以下(表4);2)为避免柱脚底板灌浆料被压碎,灌浆料强度等级提高至C80;3)为避免柱脚底板厚度过薄,混凝土所受压应力尽可能均匀。

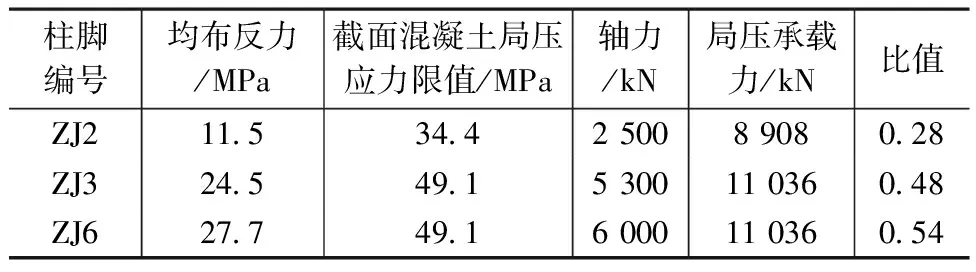
表4 混凝土局压应力校核

柱脚底板厚度通常假定底板底部应力均匀分布,根据各区块周边支承条件得到所受的最大弯矩确定[7]。本项目的柱脚底板根部所需厚度t2可根据式(5)计算求得:

(5)

式中D′为柱脚底板直径,均为525mm。

对于轴力最大的柱脚ZJ6,根据式(5)得到柱脚底板根部所需厚度达129.7mm。由于柱脚底板的反力并非均匀分布,越靠近铸钢件颈部范围反力越大,因此按传统方法确定柱脚底板厚度偏于保守。同时,由于铸钢件的截面厚度效应[5],厚度大于100mm时强度有所降低。考虑混凝土局压的影响,柱脚底板根部厚度暂按100mm设计,并通过有限元对柱脚底板承载力进行验证。

3 变截面铸钢柱脚的有限元分析

为解决设计中存在的问题,同时满足《铸钢规程》中“对于无计算公式的铸钢节点,需要进行有限元分析确保节点的安全性”的要求,对上述3种典型截面柱脚建立有限元模型,并对其承载力进行分析。

3.1 有限元模型的建立

对上述3种典型截面柱脚共建立4个模型,其中柱脚ZJ2、ZJ3仅建立空腔不贯通模型,柱脚ZJ6建立空腔不贯通模型和空腔贯通模型。模型取柱底以下1m至柱顶以上1m范围,如图5(a)所示。无缝钢管、铸钢件、锚栓及钢筋均采用理想弹塑性模型,屈服强度根据《钢标》、《铸钢规程》和《混凝土结构设计规范》(GB 50010—2010)(2015年版)[8](简称《混规》)中抗拉强度设计值选取。混凝土采用塑性损伤模型,具体参数按《混规》附录C选取。除钢筋采用T3D2单元(单元仅考虑轴向受力,不考虑剪切和弯矩)外,其余均采用C3D8R单元,网格划分如图5(b)所示。

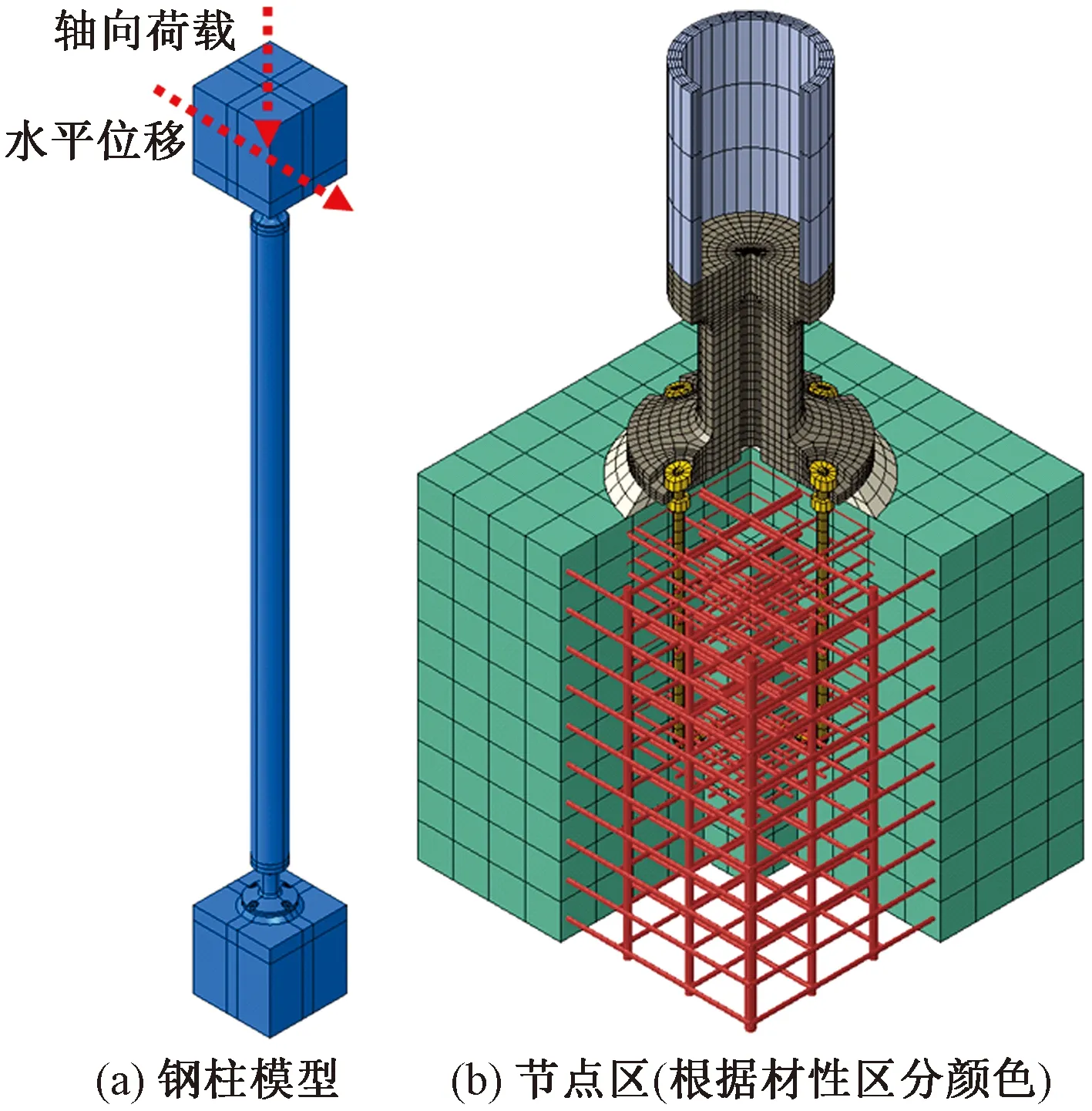
图5 有限元模型

在接触定义方面,垂直面方向采用“硬”接触,平行面方向采用库伦-摩擦力模型,混凝土与铸钢件之间摩擦系数取0.6,铸钢件与锚栓之间摩擦系数取0.3[9];钢筋与锚栓采用“嵌入”的约束方式嵌固于混凝土内。在柱底以下1m及柱顶以上1m处各设置一个参考点,将混凝土底面耦合于参考点上。对底部参考点,设置为固接;对顶部参考点,约束水平方向位移与所有方向转角。

在施加荷载时,先在柱顶参考点上施加一轴向荷载,荷载大小取最大轴力设计值;由于弯矩设计值无法根据整体模型确定,采用在柱顶参考点处施加位移荷载代替,位移取值同《建筑抗震设计规范》(GB 50011—2010)(2016年版)[10]中钢筋混凝土抗震墙结构弹性层间位移角限值(1/1 000)对应的层间位移。柱顶轴向荷载与位移荷载具体取值见表5。

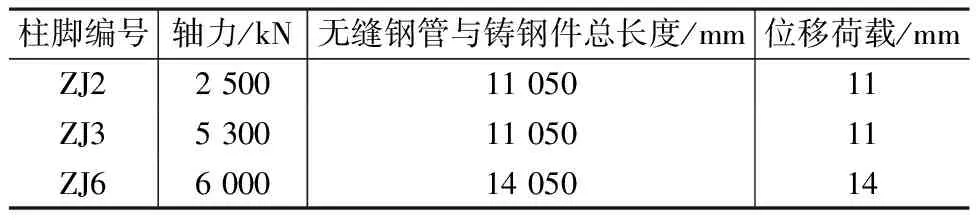
表5 柱顶轴向荷载与位移荷载取值

3.2 节点承载力分析

各柱脚模型弯矩M随顶部侧向位移Δ的变化如图6所示。由图可知,在规定的位移范围内,M随Δ的增加而呈线性增长,节点保持弹性。

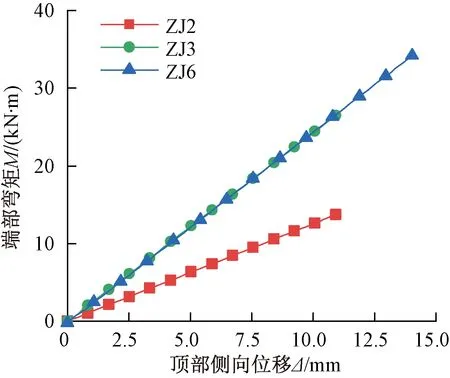
图6 各模型M-Δ曲线

铸钢件应力较大的位置集中于上下颈部倒角处,其中柱脚ZJ2、ZJ3在设计荷载下的von Mises应力均小于铸钢件抗拉强度设计值f=230MPa;柱脚ZJ6的铸钢件由于截面尺寸突变大,在上下颈部倒角处应力集中明显,局部应力超过限值230MPa。柱脚ZJ6的第一主应力云图见图8,由图8可知,柱脚ZJ6应力集中处的第一主应力为压应力。根据《铸钢规程》,当计算点各主应力全部为拉应力时,von Mises应力限值可放宽至1.2f=276MPa,故应力集中处仍可视为弹性,铸钢柱脚节点的承载力满足《铸钢规程》要求。

图8 柱脚ZJ6第一主应力云图/MPa

铸钢件颈部在规定位移下的应力并未达到抗拉强度设计值f(整体模型中钢柱侧移小于表5中的位移),说明柱脚所受的弯矩小于按钢柱固接确定的弯矩。

图9为柱脚ZJ6在Y向正应力云图,在钢管柱柱壁至铸钢颈部有明显的传力路径,说明钢管的轴力不是仅靠剪力传递至铸钢件颈部,而是一部分由该传力路径方向的压力承担。因此柱顶托盘根部所受到的弯矩明显小于按悬臂板计算结果,柱顶托盘按设计尺寸可满足承载力需求。

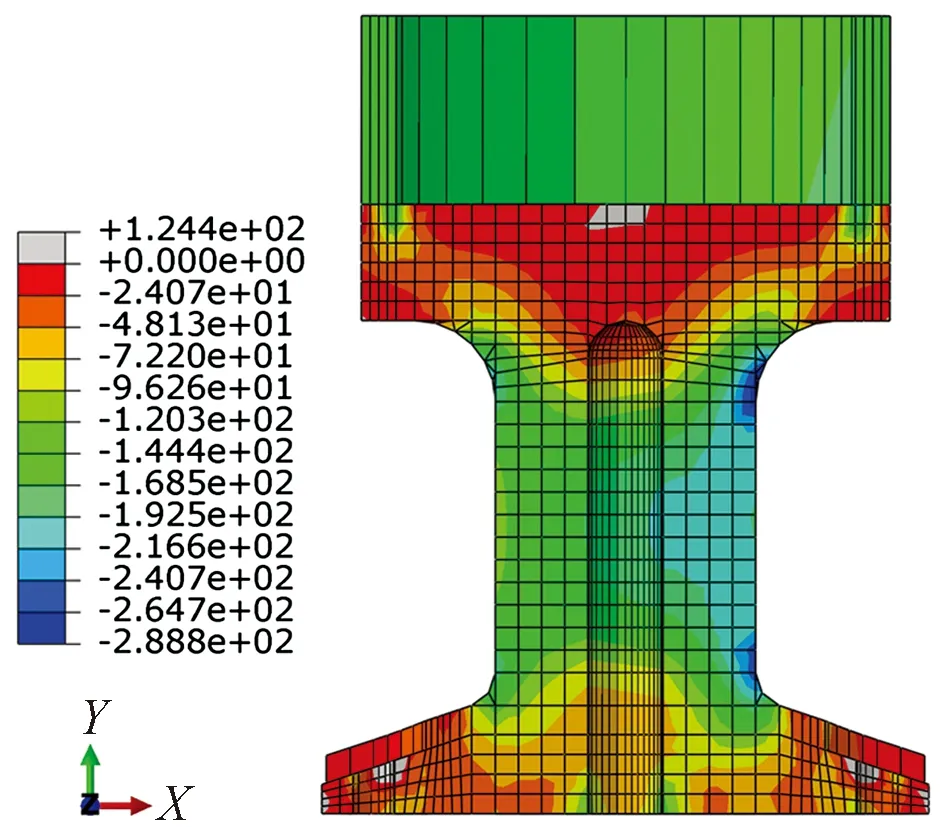
图9 柱脚ZJ6 Y向正应力云图/MPa

根据图7,柱脚底板根部厚度取100mm时承载力仍有较大富余。以柱脚ZJ6为例,混凝土基础与柱脚底板接触面上垂直于底板平面方向的应力分别如图10与图11所示。由图10、11可知,混凝土基础对柱脚的反力不是均匀分布,在铸钢件颈部对应区域应力较大,并向四周逐渐减小。混凝土所受最大压应力σc=44.1MPa,约为表4中均布反力的1.6倍;σc小于混凝土局压应力限值49.1MPa,满足规范要求。柱脚ZJ6混凝土受压损伤如图12所示,由图可得,在规定的荷载下,柱脚ZJ6混凝土未出现损伤。

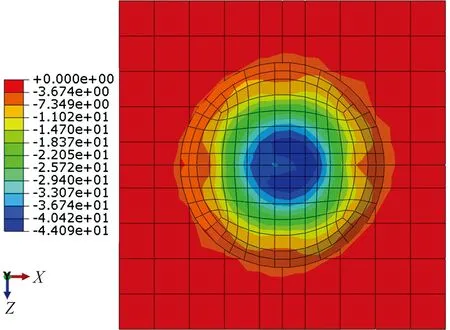
图10 柱脚ZJ6混凝土压应力云图/MPa

图11 柱脚ZJ6底板压应力云图/MPa

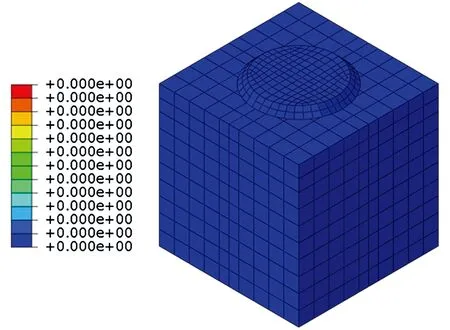
图12 柱脚ZJ6混凝土受压损伤云图

4 钢柱抗侧刚度的分析

根据图6中端部弯矩M和顶部侧向位移Δ,可定义有限元模型中柱的抗侧刚度k为:

k=V/Δ=2M/[Δ(l1+2l2)]

(6)

式中:V为钢柱所受剪力;l1、l2分别为无缝钢管和铸钢件的长度。

4.1 钢柱抗侧刚度简化模型

提出两种简化模型:1)全长范围按无缝钢管截面、两端固接(等截面模型,图13(a));2)将柱在铸钢节点长度范围视为截面同铸钢件颈部的杆件,其余部分按无缝钢管截面、两端固接(变截面模型,图13(b))。

妊娠相关内分泌疾病临床指南中，孕前检查项并不包括甲状腺功能筛查，主要筛查项目为有高危因素的孕妇，例如有个人或者家族甲状腺疾病史，甲状腺疾病亚临床状态、甲状腺抗体阳性、有流产史、早产史等孕妇。但是单纯的筛查高危孕妇无法全部有效筛查出甲状腺功能不全患者。

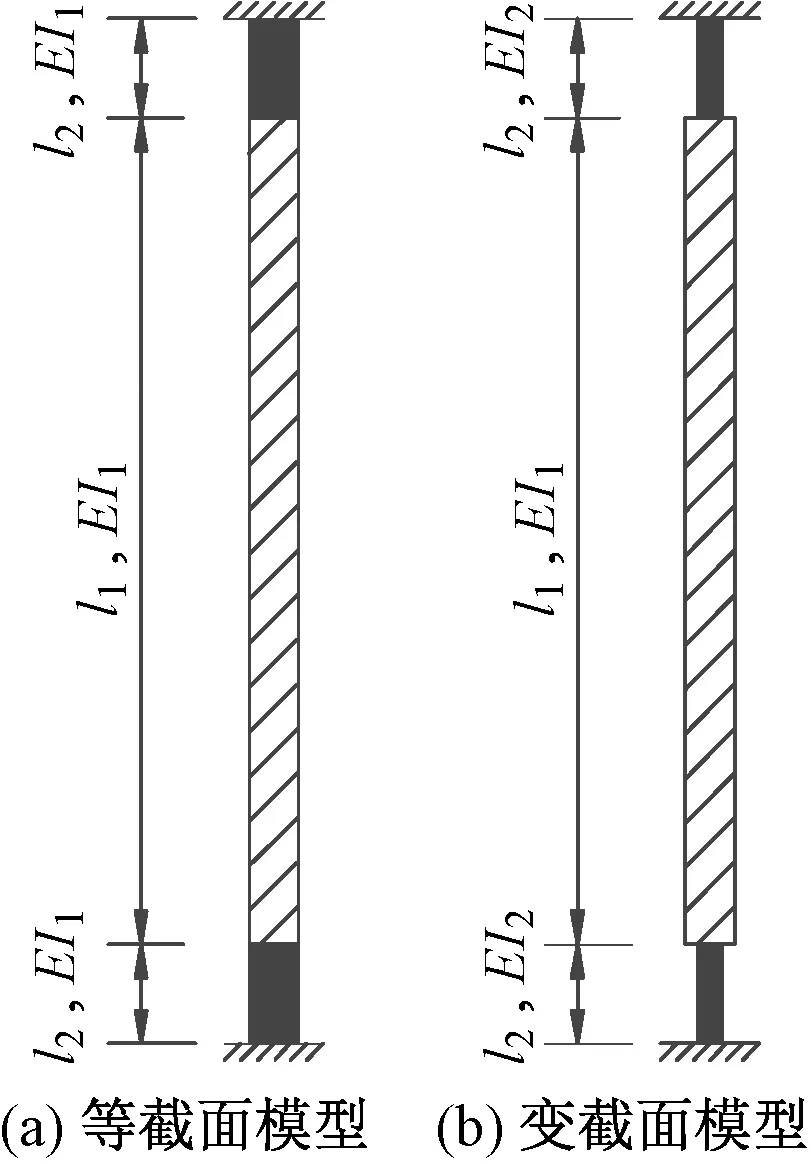
图13 钢柱简化模型

等截面模型的抗侧刚度k1与变截面模型的抗侧刚度k2可分别由式(7)与式(8)求得。

k1=12EI1/(l1+2l2)3

(7)

(8)

式中:EI1、EI2分别为钢管和铸钢件的抗弯刚度。

钢柱抗侧刚度k、k1、k2计算结果如表6所示。由表可知:

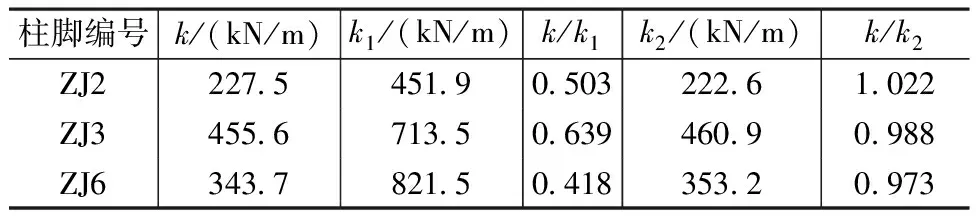
表6 钢柱抗侧刚度对比

(1) 带铸钢柱脚的钢柱具有一定的抗侧刚度,在柱顶发生侧向位移时,柱端会产生弯矩,若整体模型中柱脚节点按铰接设计,钢柱将偏于不安全。

(2) 由于端部截面减小,柱的实际抗侧刚度k为等截面模型抗侧刚度k1的41.8%～63.9%,故整体模型中,钢柱若按等截面进行设计,在相同侧向位移下,柱脚所受的弯矩为真实情况下的2倍左右,偏于保守。

(3) 不同截面下,有限元模型中柱的抗侧刚度k与变截面模型的抗侧刚度k2基本相同,误差在3%以内,钢柱按变截面模型进行设计可以较精准地反映钢柱的抗侧刚度。

由于整体模型中柱的所受轴力及高度各不相同,后文以柱脚ZJ3为分析模型进行参数分析,验证简化模型的适用性。

4.2 轴力对钢柱抗侧刚度的影响

调整分析模型的柱顶轴力,分别建立轴力分别为0、1 000、2 000、3 000、4 000、5 000、6 000、7 000kN时的模型,同时增大位移荷载至100mm。各分析模型端部弯矩M随顶部侧向位移Δ的变化如图14所示,由图可知,当钢柱轴力为1 000～4 000kN时,在设定的侧向位移下,M随Δ的增加而线性增大,节点保持弹性。随着轴压比的增大,在顶部侧向位移较大时,抗侧刚度出现明显的退化,节点区进入塑性。图15为轴力为7 000kN、顶部侧向位移为100mm时柱脚节点的等效塑性应变云图,由图可得,在较大轴力下,铸钢件受压侧屈服,锚栓与钢柱仍保持弹性。图16为轴力为0、顶部位移为100mm时柱脚节点的等效塑性应变,由图可知,塑性变形主要集中于受拉侧锚栓处,铸钢与无缝钢管仍保持弹性。当轴力为0时,钢柱抗侧刚度相较于有轴力时明显减小,且刚度退化相比高轴压比的模型更为严重。如图17所示,轴力较小时,柱脚底板与基础脱开,锚栓受拉变形。钢柱初始抗侧刚度与轴力的关系如图18所示,由图可得,当轴力不为0时,k为447～470kN/m,与变截面模型抗侧刚度k2误差在4%以内。当轴力为0时,钢柱初始抗侧刚度为406kN/m,与等截面模型抗侧刚度k1的误差达到12%。

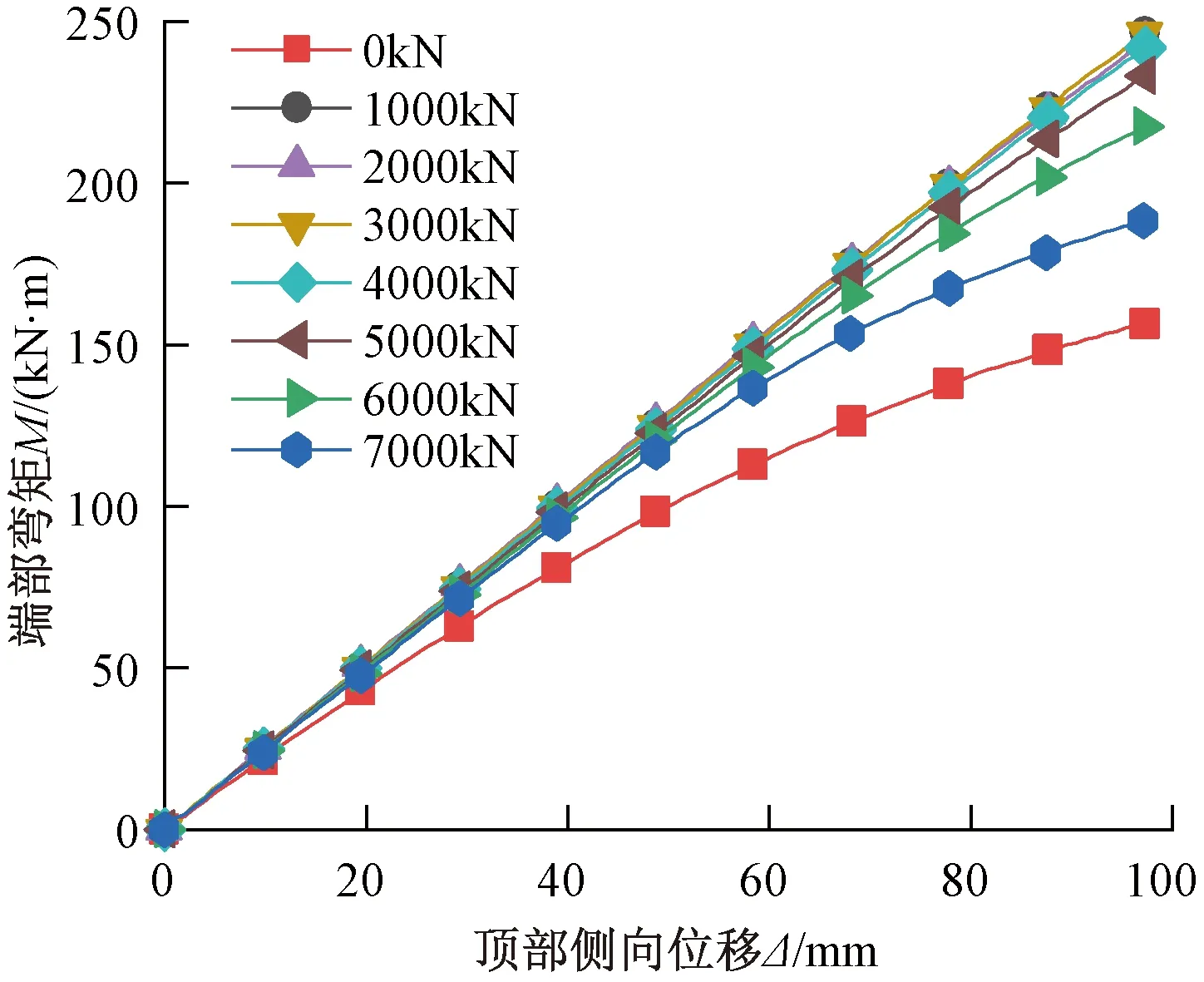
图14 不同轴力下M-Δ曲线

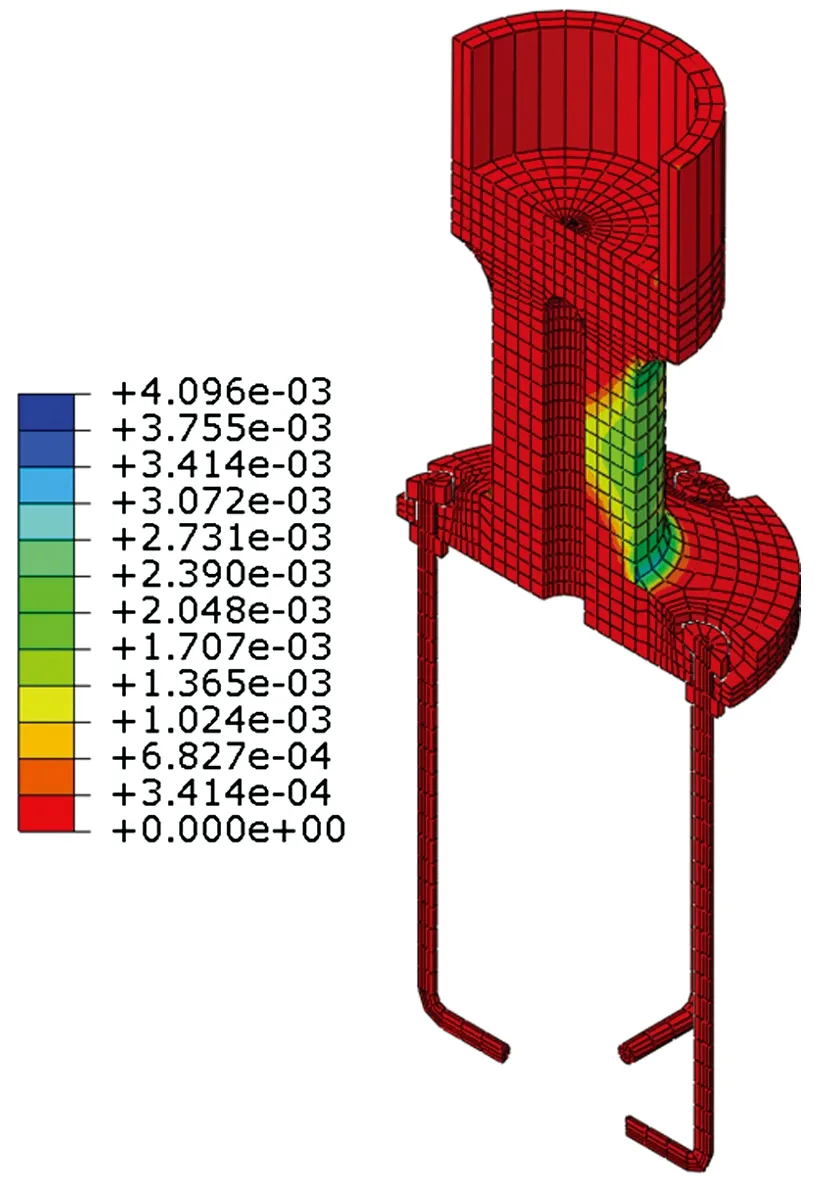
图15 轴力较大的柱脚节点等效塑性应变云图

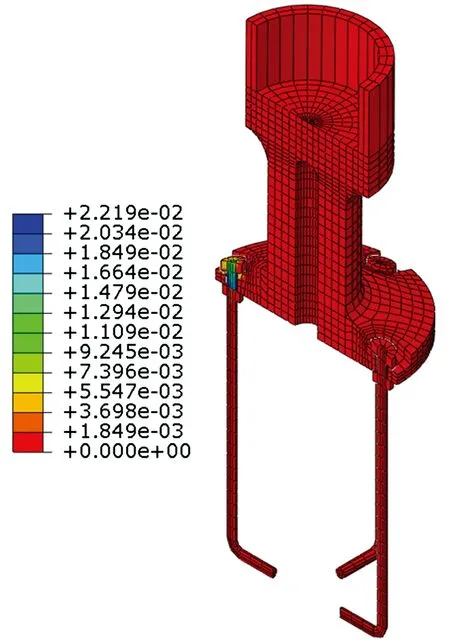
图16 无轴力时柱脚节点等效塑性应变云图

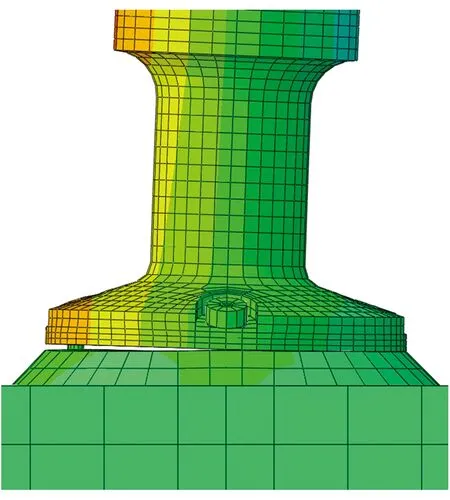
图17 柱脚底板与基础脱离

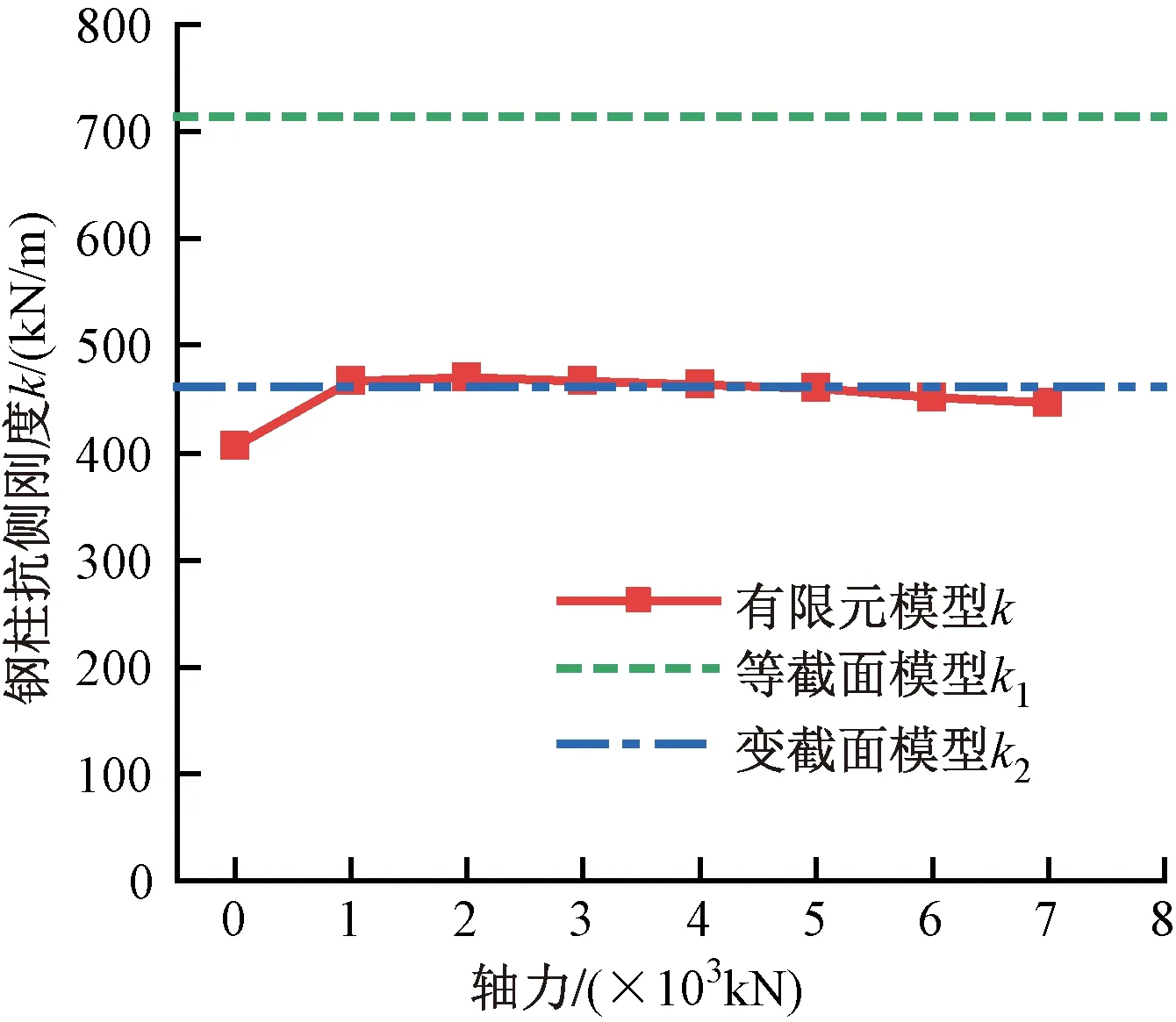
图18 钢柱抗侧刚度与轴力的关系

4.3 柱高对钢柱抗侧刚度的影响

调整分析模型中无缝钢管的长度l1,柱顶荷载取7 000kN,同时增大位移荷载至100mm。钢柱初始抗侧刚度与柱高的关系如图19所示。由图可知,不同柱高下变截面简化模型均能与有限元模型较好吻合,k2与k的误差随柱高的增大而增大,最大误差在8%以内。

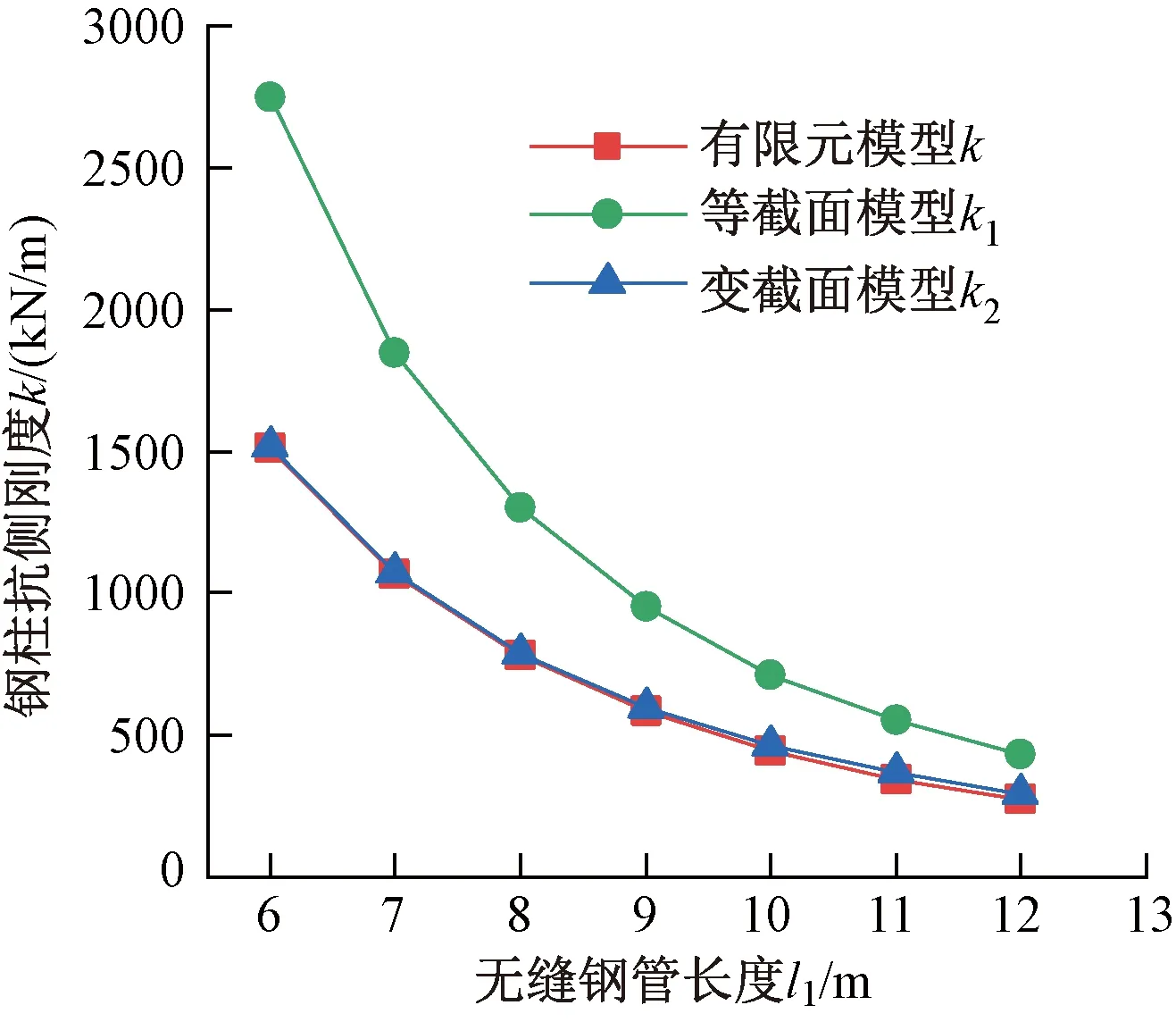
图19 钢柱抗侧刚度与柱高的关系

通过以上分析可知,在整体模型中将钢柱按变截面简化模型进行设计可以较好地反映柱脚节点的连接形式。对于轴力较小、锚栓受拉变形的钢柱,采用该简化模型的钢柱抗侧刚度偏大,钢柱在整体模型中所受弯矩相比实际中偏大,设计偏于安全。施工图设计中,按该方法对整体模型中钢柱进行建模并校核,钢柱最大应力比为0.82,铸钢颈部截面在调整后的整体模型中应力比如表7所示,由表可看出,钢铸件颈部应力比均满足设计要求。

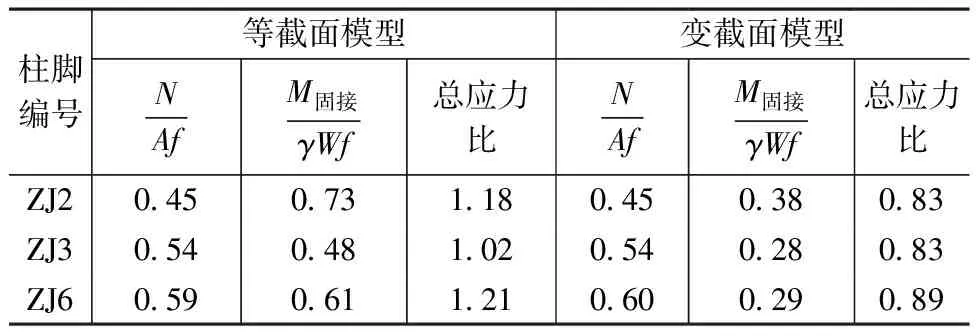
表7 各柱脚铸钢件颈部应力比对比

5 结论

(1)在设计荷载下,各铸钢柱脚节点均保持弹性,具有一定的安全储备。

(2)钢柱的轴力并不是仅靠剪力传递至铸钢颈部,而是一部分通过压力从钢柱柱壁直接传递至铸钢颈部,顶部托盘根部所受的弯矩明显小于按悬臂板计算的弯矩。

(3)柱脚底板压应力并非均匀分布,采用传统方法进行设计过于保守。柱脚底板采用初步设计的尺寸时承载力有较大富余;混凝土未发生明显损伤。

(4)设置变截面铸钢柱脚的钢柱,其抗侧刚度介于两端理想铰接与两端理想固接之间。钢柱按等截面、两端固接进行设计,会过高评价钢柱及柱脚所受的弯矩。

(5)通过对不同截面、轴力及柱高的模型抗侧刚度进行分析,将钢柱按变截面、两端固接的简化模型进行设计可以较好地反映柱脚节点的连接形式。