摩托车多连杆后悬架硬点的多目标优化
冉险生,李金波,刘兴君,余大江
(重庆交通大学 机电与车辆工程学院,重庆 400074)
0 引 言
摩托车后悬架形式多种多样,其硬点位置与行驶平顺性紧密相关。后悬架系统硬点位置的不同会直接影响其几何结构,合理的几何结构能有效提高摩托车的行驶平顺性。
国内外学者对摩托车行驶的动态特性进行了大量研究,并取得了优异的成果。T.SEGA等[1]针对多连杆悬架系统的阻尼特性,证明了改变连杆机构的几何参数可以增强悬架系统对不同道路的适应能力;S.SEGLA等[2]通过将弹簧减振器模块的下端点靠近摆臂的起点以及增加弹簧减振器模块与垂直方向的偏差(倾斜)来实现降低摩托车车身质心加速度的均方根值,从而改善摩托车的行驶平顺性;R. BARBAGALLO等[3-4]提出了一种具有偏心连杆的后悬架系统,提高了后悬架的先进性。
徐中明等[5-6]通过BikeSim与MATLAB联合仿真,针对悬架系统的阻尼和刚度特性,得到Pareto前沿;冉险生等[7]针对传统悬架系统,采用径向基函数神经网络近似模型进行多目标优化,提高了摩托车行驶的平顺性;R.BARBAGALLO等[8]、P.LEMONAKIS等[9]认为,悬架的性能可以通过驾驶员主观感受评估,也可以通过垂直加速度等客观的标准来量化。
目前对摩托车的研究主要集中在悬架系统刚度和阻尼的优化上,对摩托车多连杆后悬架结构的几何参数变化对系统平顺性的影响研究不多。
笔者以某国产大排量摩托车为研究对象,针对后悬架系统结构对摩托车行驶平顺性的影响展开研究。为了改善其行驶过程中的平顺性,在VI-Motorcycle中建立完整的摩托车多体动力学模型并进行仿真分析,通过路试试验验证了仿真模型的准确性,以车身质心俯仰振动角加速度均方根值和垂向振动加权加速度均方根值最小化为优化目标,完成多连杆后悬架系统硬点坐标的多目标优化。
1 摩托车多体动力学建模
1.1 整车模型的建立
车辆的行驶平顺性主要与车辆的垂向动力学相关。为了更好描述摩托车的垂向动力学性能,建立了四自由度模型,如图1。其平面内的振动运动可由4个独立的位移表示:簧载质量的垂直位移z、簧载质量的俯仰旋转角位移μ和2个非簧载质量的垂直位移zf、zr。
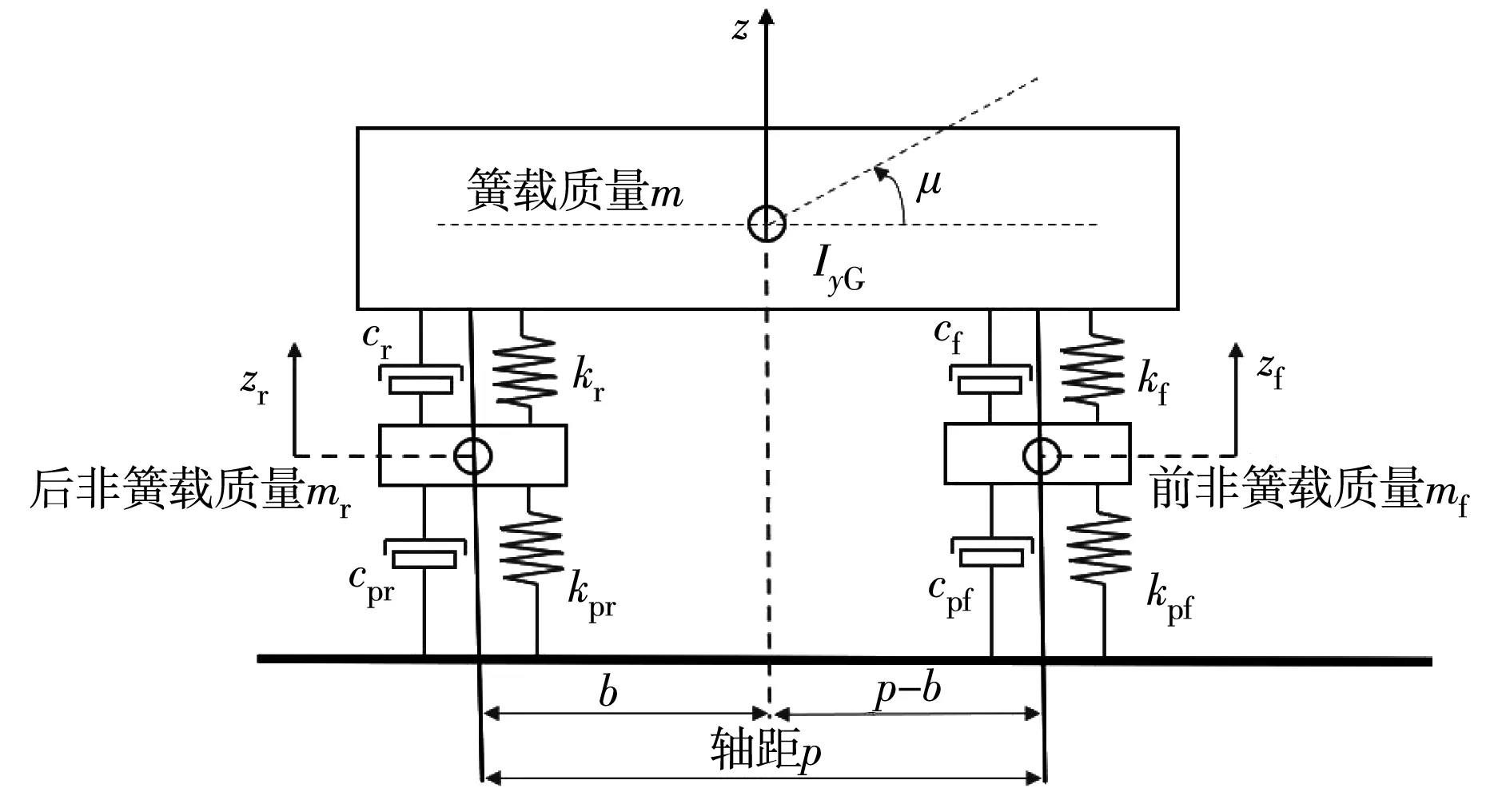
图1 四自由度整车模型Fig. 1 Four degree of freedom vehicle model
整车运动方程可用式(1)~式(5)表示:
(1)
(2)
(3)
(4)
(5)
式中:p为轴距;b为后轮轴到质心的水平距离;kf和kr分别为前、后悬架系统减震器刚度;cf和cr分别为前、后悬架系统减震器阻尼;kpf和kpr分别为前、后轮的径向刚度;cpf和cpr分别为前、后轮的径向阻尼;IyG为绕y轴的极惯性矩;m为簧载质量;mf和mr分别为前、后非簧载质量;zf和zr分别为前、后非簧载质量位移;z为簧载质量质心的位移;μ为簧载质量的俯仰旋转角位移。
在VI-Motorcycle中建立的整车模型具有5个自由度,其主要设计参数如表1,弹簧的刚度和减震器的阻尼如图2和图3。整车模型由驾驶员、车架、发动机、后摇臂、车架连杆、三角偏心连杆、上前叉、下前叉、手把管9个刚体以及前后轮组成。前后轮通过tir文件定义刚度与阻尼。驾驶员和发动机固定于车架上,可与上前叉、手把管一同看作为簧载质量m。前轮与下前叉可看作前非簧载质量mf,后轮、车架连杆、三角偏心连杆和后摇臂可看作后非簧载质量mr。因摩托车的平面运动可以看作是垂向运动与俯仰运动的组合[10],笔者主要研究摩托车的平面运动,故忽略整车模型中纵向自由度的影响,由四自由度整车模型描述车辆的振动运动(图1)。

表1 整车主要设计参数
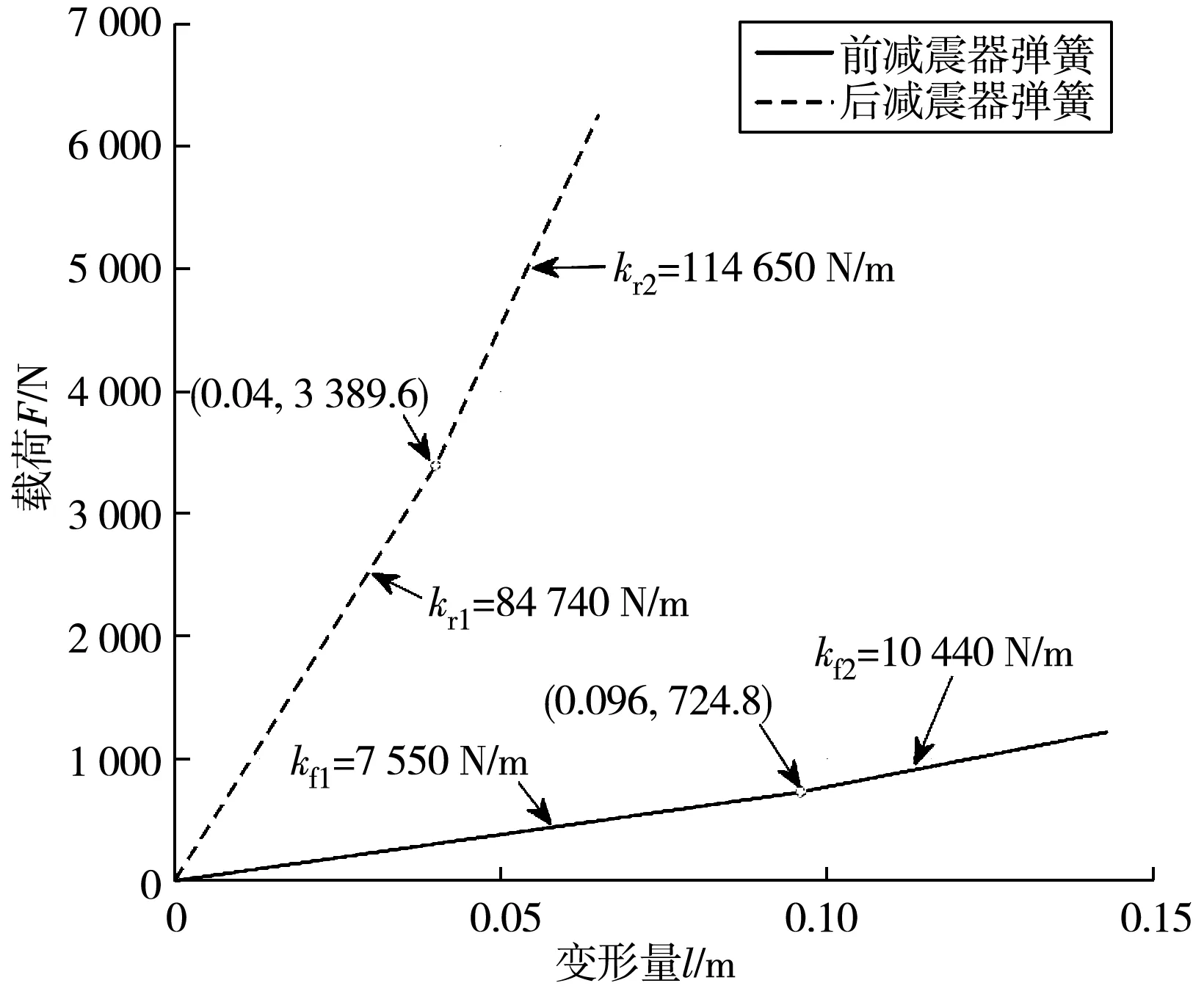
图2 前后减震器弹簧刚度曲线Fig. 2 Spring stiffness curves of front and rear shock absorbers

图3 前后减震器阻尼曲线Fig. 3 Damping curves of front and rear shock absorbers
1.2 多连杆后悬架硬点位置
传统的后悬架系统中减震器直接与后摇臂相连接,具有结构简单、加工方便等优点,但是这种后悬架的缺点为不具有好的渐进性。
多连杆后悬架系统是目前国外大排量摩托车中比较流行的一种后悬架,其减震器不直接与后摇臂相连,如图4。V. COSSALTER等[10]认为,多连杆后悬架系统与传统后悬架系统相比具有更好的渐进性。
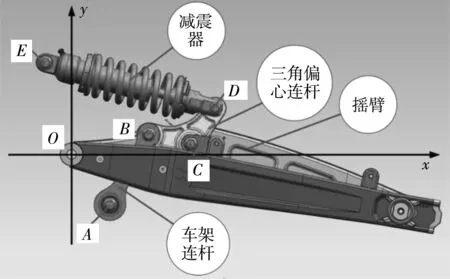
图4 多连杆后悬架系统Fig. 4 Multi-link rear suspension system
笔者主要研究多连杆后悬架系统的结构对摩托车行驶平顺性的影响。后悬架主要硬点参数如表2,初始硬点位置如图4。其中,O点为后摇臂旋转中心位置,其坐标为(0,0,0);ED为减震器;BCD为一个三角偏心连杆;AB为与车架相连接的连杆。最终在VI-Motorcycle中建立的多连杆后悬架模型如图5。
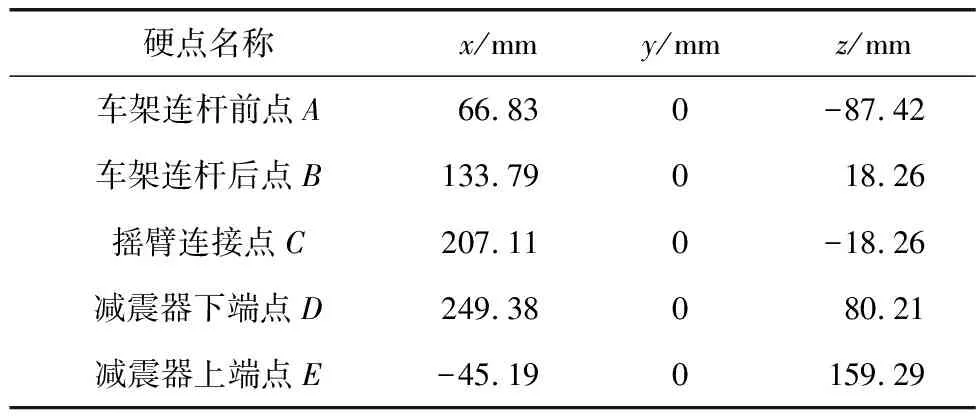
表2 后悬架主要硬点参数
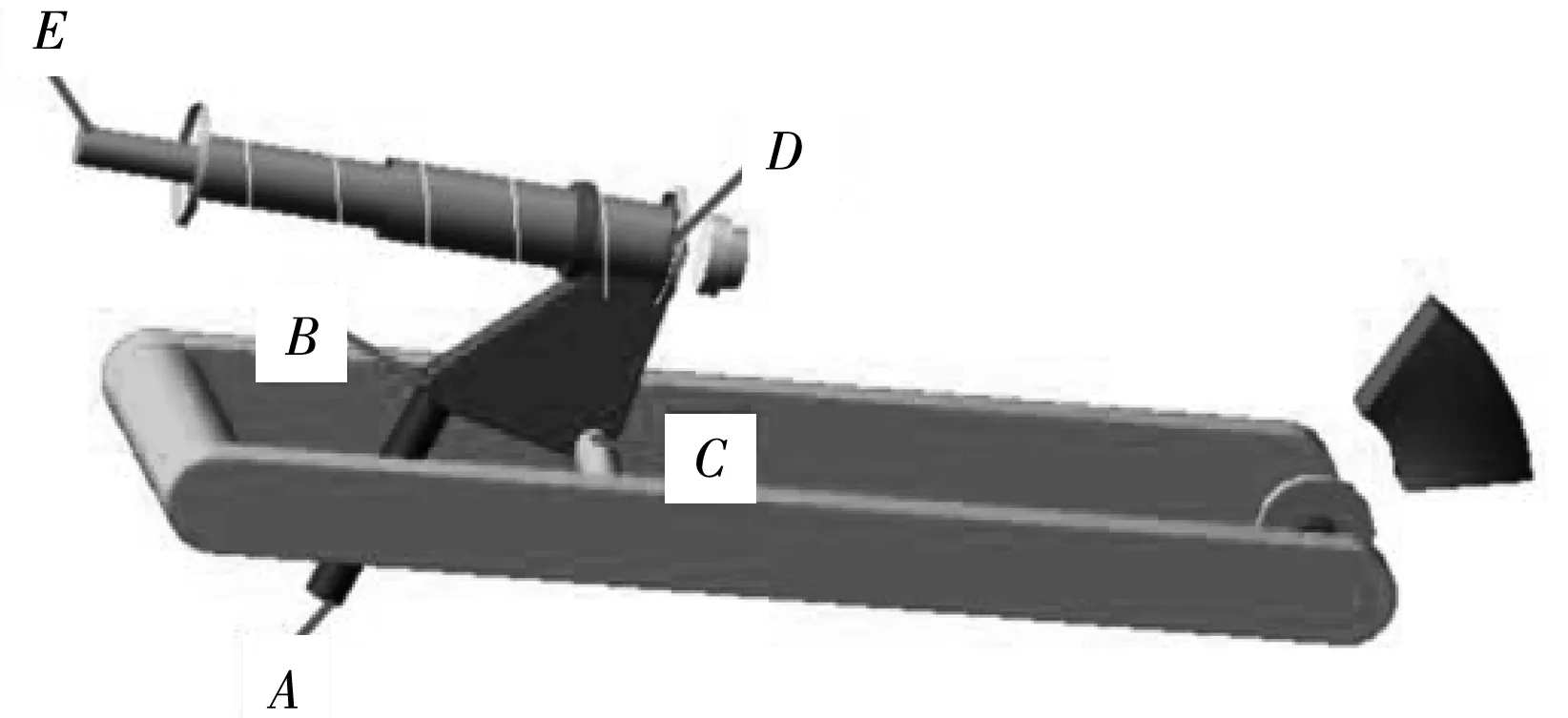
图5 后悬架系统多体模型Fig. 5 Multi-body model of the rear suspension system
1.3 路面模型的建立
根据GB/T 7031—2005《机械振动 道路路面谱测量数据报告》道路分级要求,采用谐波叠加法[5]对C级路面不平度进行模拟,建立道路高程随道路长度变化的模型,其表达式如式(6):
(6)
式中:X为道路纵向位移;θ为[0,2π]之间的随机数;Gd(nmid_i)为空间功率谱密度;nmid_i为空间频率。
由式(6)通过MATLAB编写C级路面程序,得到C级路面不平度,如图6。

图6 C级路面不平度Fig. 6 Roughness of C level road
2 实车验证
为了确保所建立仿真模型的准确性,需要通过实车试验对其进行验证。
2.1 路试试验系统
笔者所采用的测试系统为德国2D DTS(动态测试系统),试验的设备有IMU(惯性测量单元)、GPS传感器、显示器和数据采集仪,试验的系统框架如图7。其中,GPS传感器[11]用于获得摩托车的速度和位置;IMU测量其俯仰振动与垂向振动加速度;显示器用于驾驶员掌握车辆相关信息;最后通过数据采集仪接收测得的数据并储存。
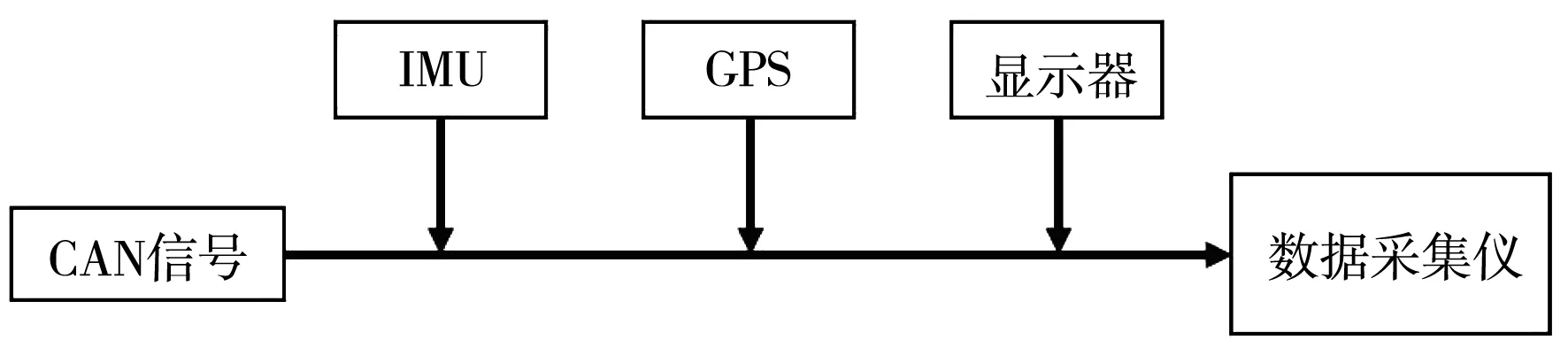
图7 试验系统框架Fig. 7 Experiment system framework
实车试验时,IMU安装在接近车辆质心的油箱附近,显示器安装在邮箱前部,方便驾驶员及时掌握车辆动态情况,GPS固定在摩托车尾部,数据采集仪安装在车头左部的覆盖件上。
2.2 模型验证
通过搭建的路试试验系统,参照GB/T 4970—2009《汽车平顺性试验方法》,由专业的驾驶员在C级路面上以60 km/h的速度匀速直线行驶,通过多次试验以减少人为误差。
经过实车试验与仿真结果进行对比分析,俯仰振动加速度均方根值与垂向振动加权加速度均方根值如表3,车身质心俯仰振动角加速度和垂向振动加速度功率谱密度(PSD)如图8和图9。
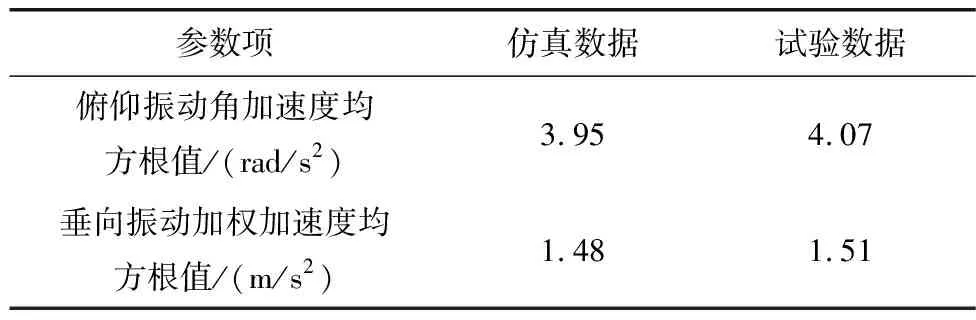
表3 仿真与试验加速度均方根值对比
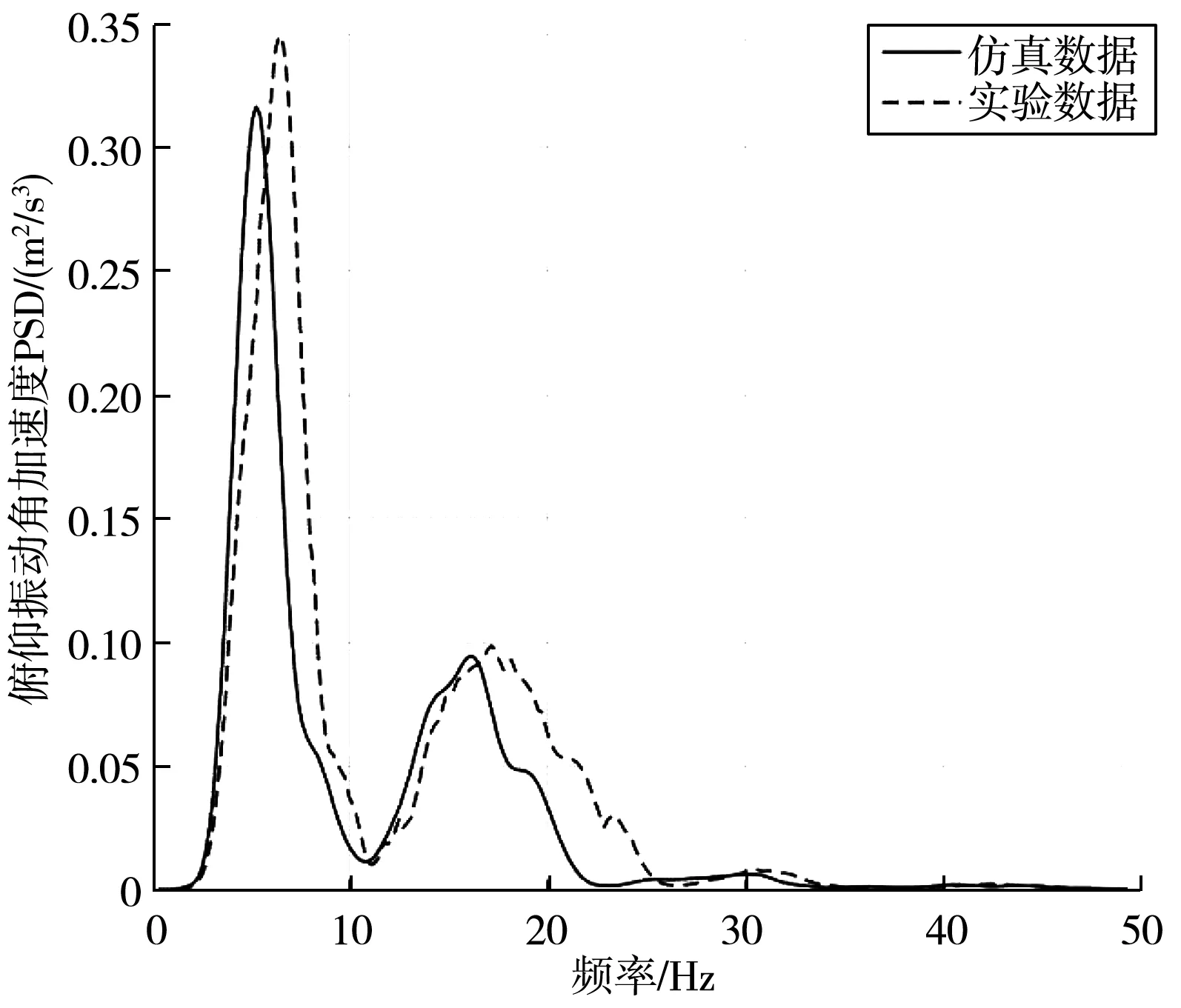
图8 车身质心俯仰振动角加速度PSD对比Fig. 8 Contrast of body mass center pitch vibration angular acceleration PSD
仿真数据表明,车身质心俯仰角加速度均方根值为3.95 rad/s2,车身质心垂向加权加速度均方根值为1.48 m/s2。试验数据表明,车身质心俯仰角加速度均方根值为4.07 rad/s2,车身质心垂向加权加速度均方根值为1.51 m/s2。
由图8、图9可知,仿真数据与试验数据拟合程度较高,证明了模型的准确性。由于受驾驶员、试验场地和天气等不确定因素影响,试验数据与仿真数据相比存在一定误差,但该误差在可接受范围内[12]。
3 多目标优化
3.1 多目标数学模型的建立
为了改善该车辆在随机路面上的行驶平顺性,以该车辆后悬架硬点坐标为设计变量,以车身质心俯仰振动角加速度均方根值和垂向振动加权加速度均方根值最小化为优化目标,采用NSGA-Ⅱ 算法进行多目标优化。由于该车辆后悬架系统硬点在xOz平面,即硬点的y坐标为0,所以仅对硬点在xOz平面进行优化,建立该多目标优化的数学模型如式(7):
(7)
式中:σrms_p与σrms_v分别为车身质心俯仰角加速度均方根值与车身质心垂向振动加权加速度均方根值;Ax∈R1;Az∈R2;Bx∈R3;Bz∈R4;Cx∈R5;Cz∈R6;Dx∈R7;Dz∈R8;Ex∈R9;Ez∈R10;R1,R2,…,R10分别为对应各个变量的取值范围。
由于车辆后悬架系统结构的限制,自变量的取值范围[13]为初始值的±20 mm,如表4。

表4 设计变量取值范围
带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)将拥挤度计算和精英策略同时考虑在内,有效地避免了在优化过程中的局部收敛问题。根据Pareto最优解概念,Pareto最优前沿中的个体可以均匀地扩展到整个解空间,保证了种群的多样性,具有鲁棒性、全局最优性、高效并行性、不要求函数连续可导等特点[14-15]。据此,文中优化算法采用NSGA-Ⅱ遗传算法,设置的主要参数如下:种群数量为40,遗传代数为25,交叉概率为0.9。通过iSIGHT集成VI-Motorcycle搭建联合仿真平台,利用MATLAB对数据进行自动化处理,建立的优化流程如图10。
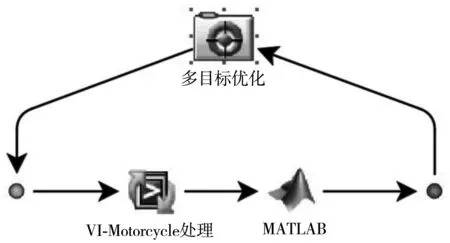
图10 优化流程Fig. 10 Optimization process
3.2 优化结果
经过1 000次迭代计算,完成优化分析。其中,目标函数的迭代寻优过程如图11、图12,在迭代937步后找到最优解。
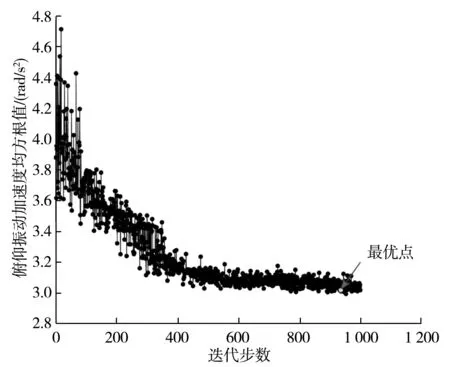
图11 车身质心俯仰振动角加速度均方根值寻优过程Fig. 11 Optimization process of pitch vibration angularacceleration RMS of body mass center
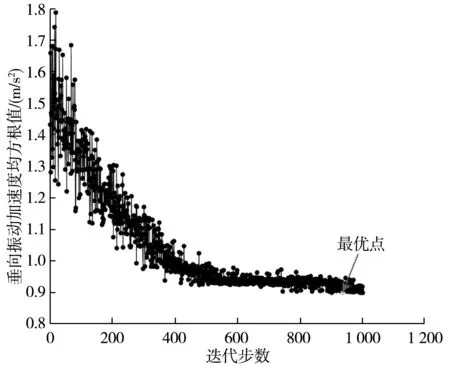
图12 车身质心垂向振动加权加速度均方根值寻优过程Fig. 12 Optimization process of vertical vibration weighted acceleration RMS of body mass center
优化前后的设计变量取值如表5,优化后除了B点的z坐标和C点的x坐标值增大,其余值均减小,优化前后的硬点对比示意如图13。
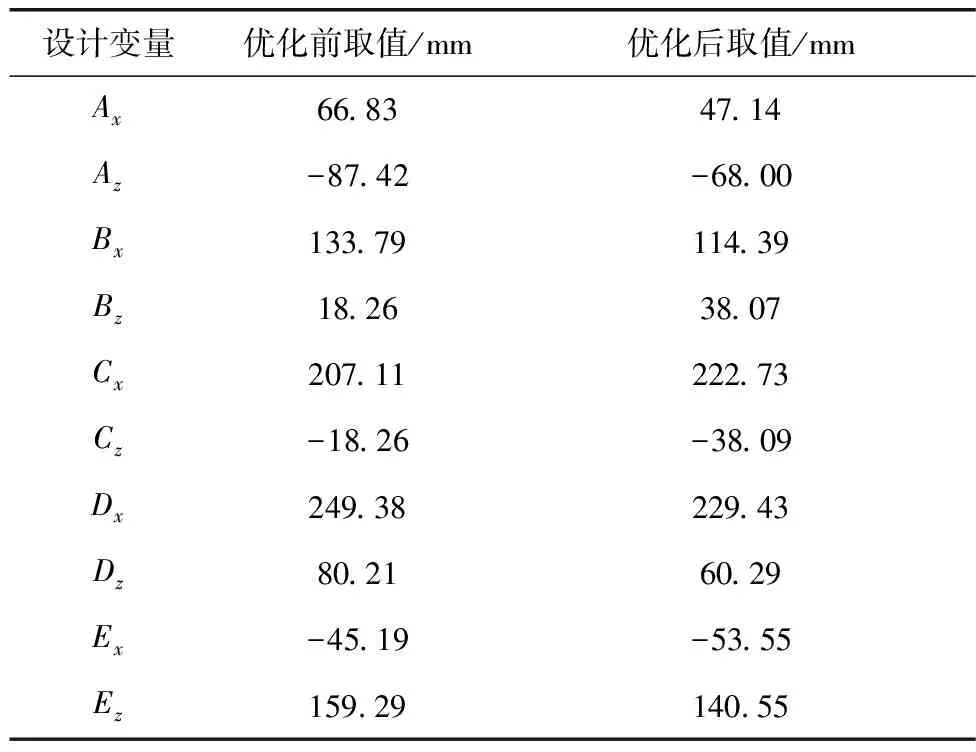
表5 设计变量优化前后取值
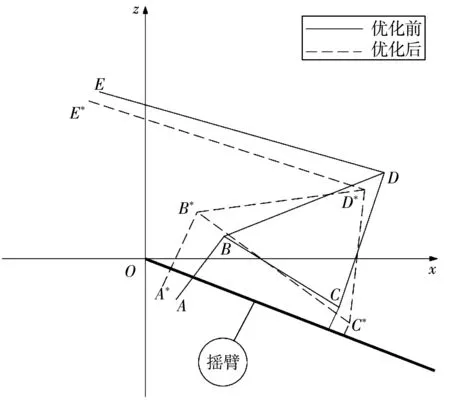
图13 优化前后悬架硬点示意Fig. 13 Schematic diagram of suspension hard points before and after optimization
优化前与优化后的加速度功率谱密度如图14、图15,目标响应结果如表6。图14、图15、表6可看出,优化后俯仰振动角加速度均方根值为3.00 rad/s2,相较于优化前降低了24.0%;车身垂向振动加权加速度均方根值为0.90 m/s2,相较于优化前降低了39.2%;优化后振动明显下降,车辆的行驶平顺性有明显改善。由于悬架系统硬点位置改变使得后悬架系统的刚度和阻尼发生了变化,从而导致优化后峰值幅值降低,峰值频率略有减小。在不考虑悬架撞击限位现象情况下(极限情况),达到了预期的优化目标,同时也表明该优化方案的有效性。

表6 优化后前后目标响应
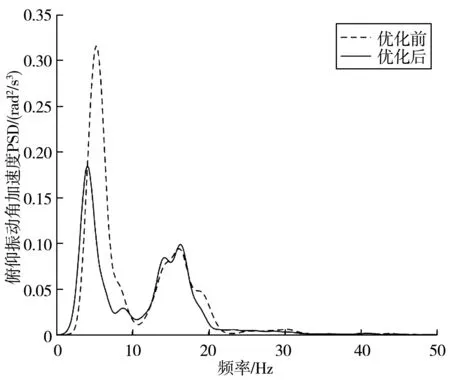
图14 优化前后车身质心俯仰振动角加速度PSD对比Fig. 14 Comparison of body mass center pitch vibration angularacceleration PSD before and after optimization
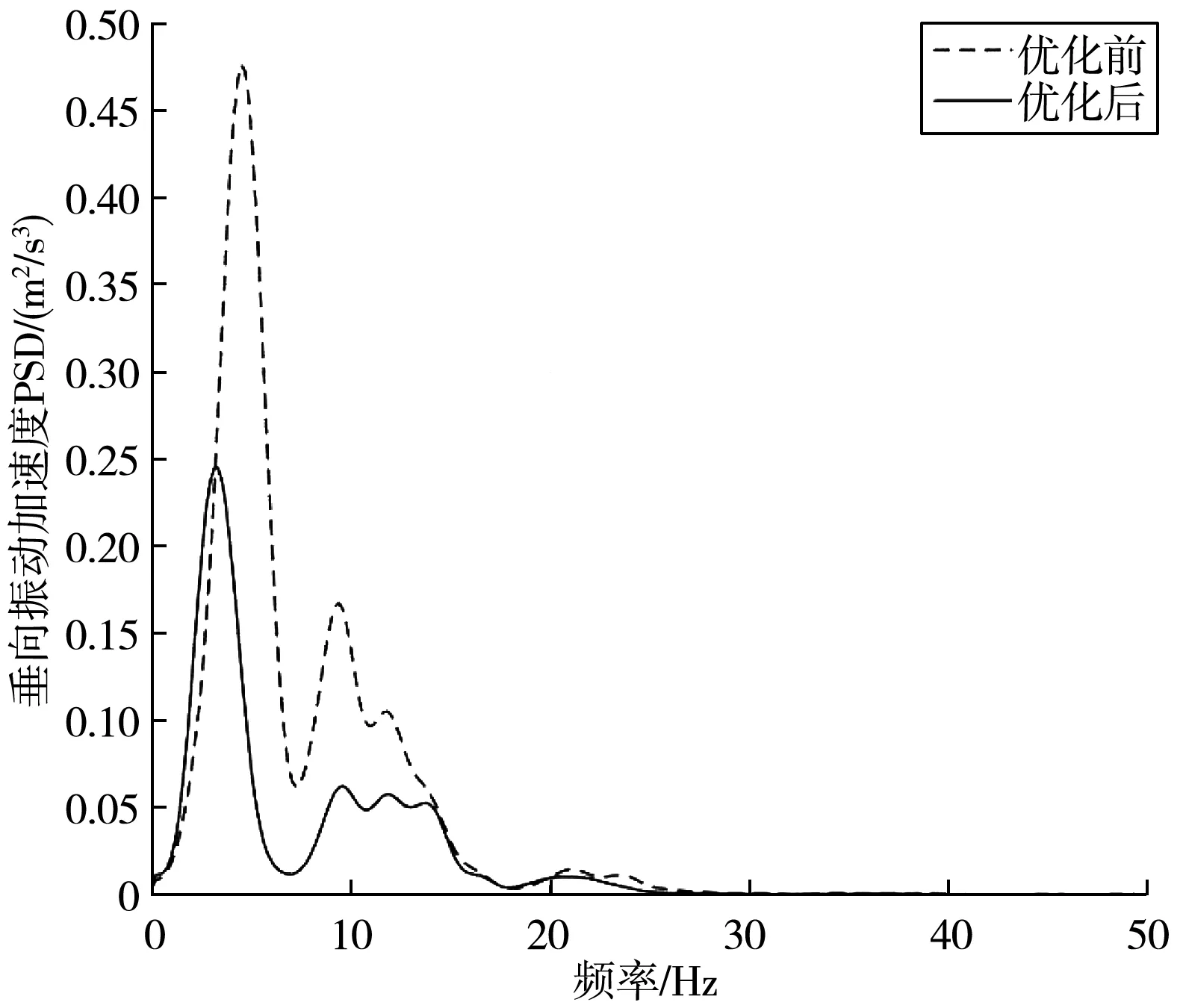
图15 优化前后车身质心垂向加权加速度PSD对比Fig. 15 Comparison of vertical weighted acceleration PSD of body mass center before and after optimization
4 结 论
1)采用摩托车动力学软件VI-Motorcycle建立准确的整车、路面和驾驶员模型,考虑到该车辆在行驶时的俯仰振动和垂向振动问题,对车辆进行了平顺性仿真分析,提出用改变后悬架硬点坐标的方法改善摩托车的行驶平顺性。
2)将实车试验与优化前摩托车的车身质心俯仰振动角加速度PSD和垂向振动加速度PSD进行对比分析,结果表明,仿真数据与试验数据吻合程度较高,证明了模型的准确性。
3)以摩托车的车身质心俯仰振动角加速度均方根值和垂向振动加权加速度均方根值为优化目标,以后悬架系统硬点的x坐标和z坐标为自变量,对后悬架系统的硬点在xOz平面进行多目标优化,使得摩托车的俯仰振动角加速度均方根值和垂向振动加权加速度均方根值均减小,实现了预期的优化目标。车辆的行驶平顺性得到改善,表明了该优化方案的有效性。

