摩托车交通事故严重程度多尺度空间异质性分析

潘义勇,缪炫烨,吴静婷

(南京林业大学 汽车与交通工程学院,江苏 南京 210037)

0 引 言

随着我国经济水平的提高,摩托车新注册登记数量随之增加,根据公安部发布的数据, 2022年全国新注册登记摩托车1 130万辆,同比增长12%。摩托车驾驶员作为交通参与者的弱势方,在没有车厢保护,且防护措施不完善的情况下,容易受到交通事故的严重伤害[1],因此有必要对摩托车交通事故严重程度的影响因素进行分析。

国内外学者对交通事故严重程度的影响因素进行了研究,离散选择模型多用于研究影响因素的异质性。胡骥等[2]通过构建有序Logit模型研究了翻车事故严重程度的影响因素;秦雅琴等[3]通过构建多项Logit模型研究了摩托车交通事故严重程度的影响因素;M.ISLAM[4]利用考虑均值方差异质性的混合Logit模型,研究了年龄对摩托车交通事故严重程度的影响;C.SE等[5]构建了考虑均值异质性的随机参数有序Probit模型,研究了城乡地区摩托车交通事故严重程度的影响因素;M.WASEEM等[6]构建了考虑均值方差异质性的随机参数Logit模型,研究了摩托车交通事故严重程度的影响因素。上述研究在采用离散选择模型研究交通事故严重程度的影响因素时,并未对影响因素的空间异质性进行分析,但是空间异质性对交通事故严重程度的影响需要纳入考虑。

地理加权回归模型(geographically weighted regression,GWR)是研究空间异质性的主流模型,在交通领域被广泛应用。J.LIU等[7]利用GWR模型研究了肇事逃逸事故严重程度的影响因素;M.T. RAHMAN等[8]在研究交通事故黑点与土地利用的关系时,构建了GWR模型来捕捉潜在的空间异质性;H.YANG等指出,并非所有的变量都会在空间上发生变化[9],因此H.YANG等[10]构建混合GWR模型,允许GWR模型中存在局部变量和全局变量,研究了共享单车使用情况影响因素的空间异质性。此外,部分学者在传统GWR模型的基础上增加考虑了时间维度,J.LIU等[11]构建了GTWR模型研究了酒后驾车事故的时空异质性;X.XU等[12]构建了GTWR模型探索了行人交通事故影响因素的时空异质性。上述研究中采用的模型均为传统GWR模型或相关改进模型,但这些模型对影响因素的空间异质性尺度的研究并不完善。

在地理空间的相关研究中,尺度的概念十分重要。多尺度地理加权回归模型(multi-scale geographically weighted regression, MGWR)考虑了系数间差异化的异质性尺度,通过允许每个自变量拥有各自不同的空间平滑水平,对影响因素的空间异质性程度定量分析,从而回归出更接近真实情况的空间关系模型[13]。目前,该模型还未全面应用到摩托车交通事故严重程度影响因素的空间异质性研究中。

综上,笔者采用MGWR模型对摩托车交通事故严重程度的影响因素进行分析。首先对事故数据进行筛选和统计性描述;再阐述MGWR模型的基本原理和检验原理;然后利用通过检验后的自变量构建MGWR模型做回归分析,标定模型结果;最后,结合模型回归出的影响因素的带宽和系数,定量分析影响因素的空间尺度和显著影响因变量的影响因素的空间异质性。

1 数据描述与变量选取

基于美国某州交通事故数据库,提取了2015—2019年共5 a的摩托车交通事故数据。首先对数据库中的原始数据进行预处理:数据库中涉及到交通事故主要信息的表为“Events”、“Drivers”和“Vehicles”,利用STATA软件将3个表按照唯一的事故编号进行横向匹配,剔除掉交通事故信息记录缺失的数据,得到18 499条摩托车交通事故数据。

选取的因变量为摩托车交通事故严重程度,美国高速公路管理局将交通事故严重程度分为5类(KABCO),其中:K(fatal injury)指事故发生后30 d内人员死亡;A(incapaciting injury)指人员受伤,并且需要送往医院进行医疗救助;B(non-incapacitating injury)指人员受到非失能性伤害,如割伤、擦伤等;C(possible injury)指人员可能受伤,即人员无外伤但自述有疼痛的感觉或意识不清;O(no injury)指人员未受伤。交通事故数据交通事故数据的因变量的描述性统计如表1。

横向匹配后的18 499条事故数据由事故本身数据、驾驶员数据和车辆数据3部分组成。结合数据库中记录信息完整的数据,从人、车、路、环境共4个方面尽可能全面选择候选自变量参与模型分析,候选自变量的描述性统计如表2。

表2 候选自变量描述性统计

2 模型方法

2.1 多尺度地理加权回归模型

MGWR模型是在传统GWR模型的基础上优化得到的,传统GWR模型在进行回归分析时,每个自变量的带宽固定。但不同自变量的尺度往往不完全一致,固定带宽可能会使模型估计的结果产生偏差。MGWR模型通过放宽“所有局部系数的空间过程的尺度是相同的”这一假设,构建更接近真实情况的模型。MGWR模型的计算公式如式(1):

(1)

式中:yi为样本点i的交通事故严重程度的观测值;βbj(·)为带宽为b的第j个局部回归系数函数,其中bj为第j个变量回归系数使用的带宽,其物理意义为邻近样本点的数量;(ui,vi)为样本点的空间地理位置;xij为变量j在i处的观测值;εi为随机误差项。

2.2 空间自相关检验

在构建MGWR模型前需要检验变量间的空间自相关性。全局莫兰指数I用来确定变量在空间上是否相关及关联程度如何,Z得分用来对全局莫兰指数的显著性进行评估。两者的计算如式(2)、式(3):

(2)

(3)

2.3 拟合优度检验

在确定MGWR模型的最优带宽时,选用修正后的赤池信息准则(用AAICc值表示)来确定最优带宽,如果两个模型的AAICc值相差大于3,具有较低AAICc值的模型将被视为更佳的模型。AAICc值的计算如式(4):

(4)

令AAICc取最小值,即可求得对应矩阵的迹,进而得到最优带宽。

2.4 多重共线性检验

对候选自变量进行相关性测试以避免共线性问题,方差膨胀因子(用VVIF值表示)用来检验指标的冗余度,当变量的VVIF>7.5时,表示指标存在冗余。VVIF值的计算公式如式(5):

(5)

式中:Ri为第i个候选自变量对其余候选自变量做回归分析的负相关系数。

3 模型估计

3.1 多重共线性检验结果

通过构建OLS模型计算候选自变量的VVIF,利用逐步回归法剔除存在多重共线性和未通过显著性检验的自变量,最终纳入模型的自变量见表3,表中为归一化的结果。

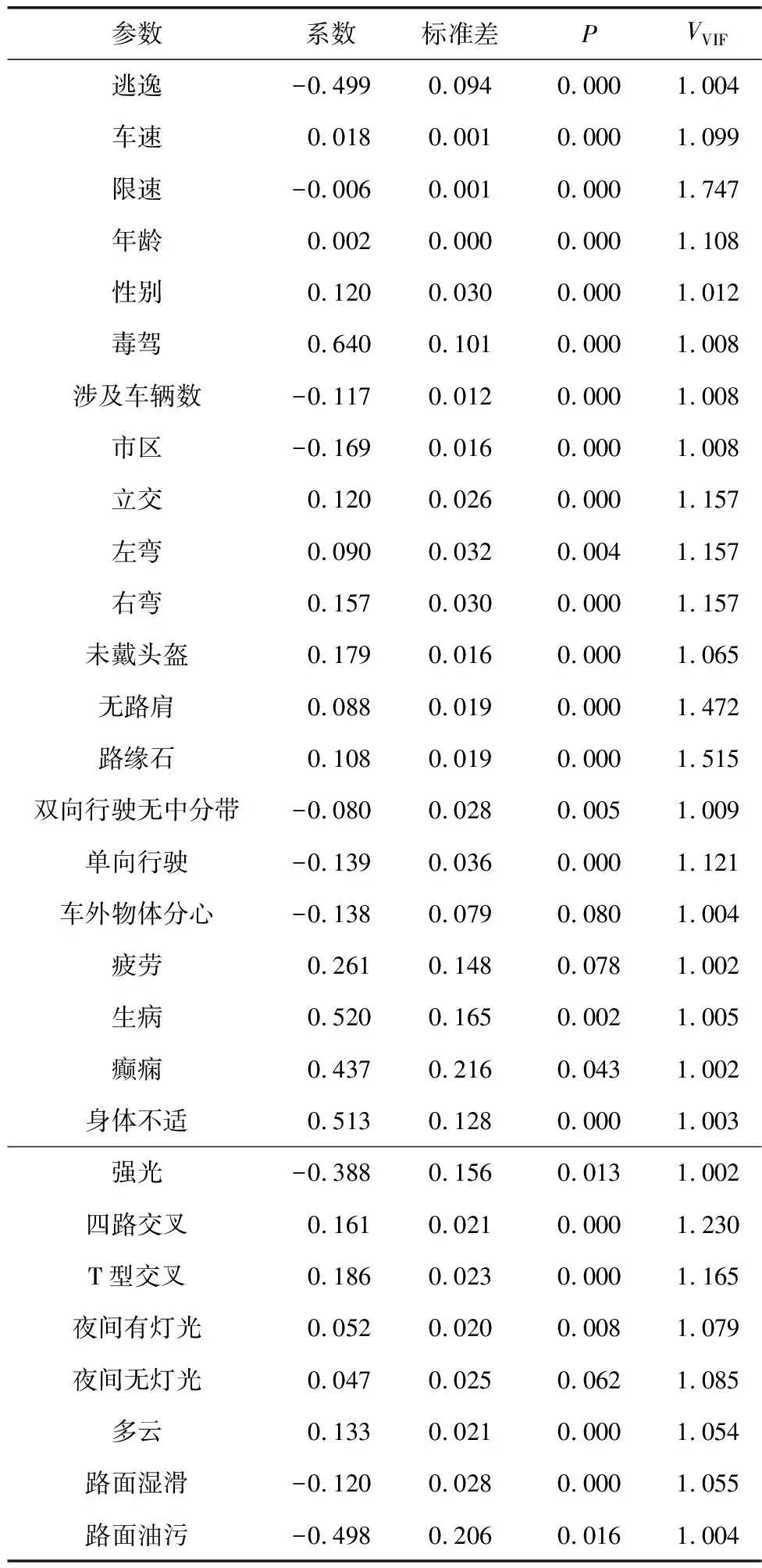
表3 OLS模型参数回归结果

从表3可以看出,最终纳入模型的自变量的VVIF值范围为[1.002,1.747],均小于7.500,P值均小于0.100,说明最终纳入模型的自变量不存在指标冗余且显著。

3.2 空间自相关检验结果

利用ARCGIS软件对摩托车交通事故严重程度做全局空间自相关检验。因变量的全局莫兰指数为0.227,说明因变量具有空间正相关性;Z得分为15.706,远大于临界值2.580,说明因变量观测值具有明显的聚类特征,且随机产生此聚类模式的可能性小于1%,即在1%的显著水平下,摩托车交通事故严重程度存在显著全局空间自相关。

但是全局莫兰指数无法表现出局部地区的空间集聚类型,因此在全局自相关检验的基础上,结合局部莫兰指数绘制LISA聚类图,分析摩托车交通事故严重程度的局部聚集特征。

局部莫兰指数可以识别随空间位置不同而可能存在的不同空间关联模式,从而观察空间局部不平稳性。若局部莫兰指数显著为正且标准化后的观测值大于0,表示样本点与其邻居的观测值相对较高,属高高集聚;若局部莫兰指数显著为正且标准化后的观测值小于0,表示样本点与其邻居的观测值相对较低,属低低集聚;若局部莫兰指数显著为负且标准化后的观测值大于0,表示邻居观测值远低于样本点的值,属高低集聚;若局部莫兰指数显著为负且标准化后的观测值小于0,表示邻居观测值远高于样本点的值,属低高集聚。摩托车交通事故严重程度的LISA聚类图如图1。

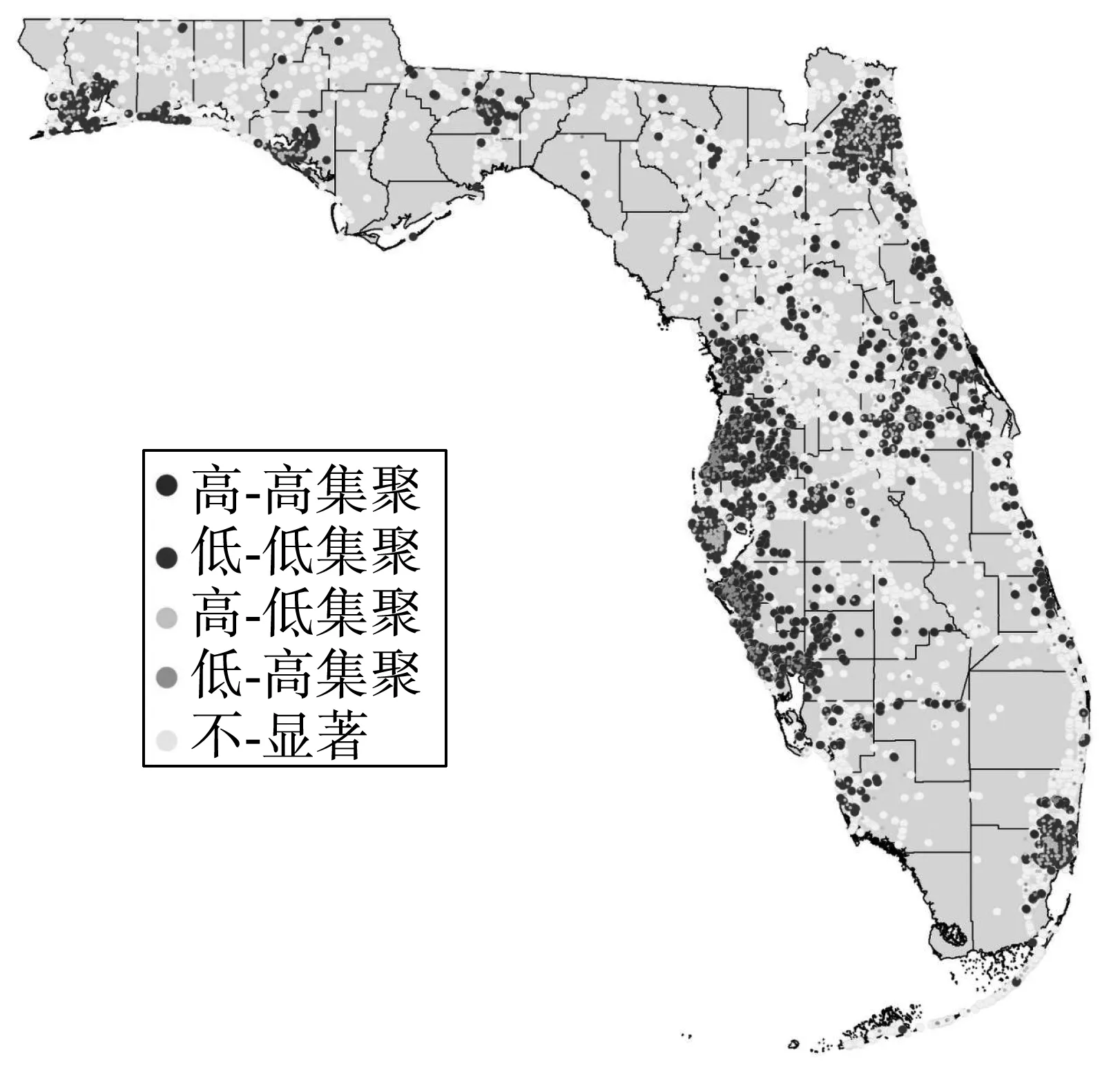
图1 摩托车交通事故严重程度LISA聚类图Fig. 1 LISA clustering map of motorcycle traffic accident severity

从图1可以看出,该州的中西部地区出现显著的“高-高”集聚区,在该州的西北角和东北角处的地区以“低-低”集聚区为主,其余地区则分散着“高-低”集聚和“低-高”集聚。总体来说,该州“高-高”集聚区和“低-低”集聚区分布范围较广,呈集中分布特征,“高-低”集聚和“低-高”集聚区域则呈现相对分散的布局。

3.3 多尺度地理加权回归模型结果

利用3.1节中通过多重共线性检验且显著的自变量构建MGWR模型,并与OLS模型、GWR模型进行指标对比如表4,表中调整后的R2为一种判定系数,可衡量回归模型。

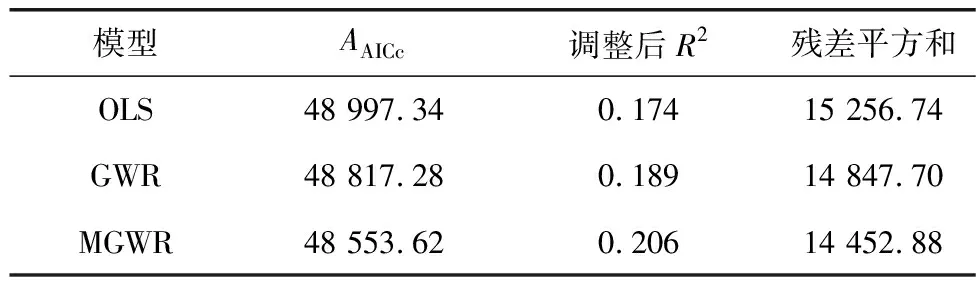
表4 OLS、GWR、MGWR回归模型指标

从表4可以看出,MGWR模型的AAICc值和残差平方和均明显小于OLS模型和GWR模型,说明MGWR模型得到了更接近真实情况的回归结果。此外,MGWR的调整后R2值高于OLS模型和GWR模型,说明MGWR模型的结果优于GWR模型。

MGWR模型回归参数结果如表5,表中为归一化后的结果。

从表5的回归结果可以初步看出:

1)部分自变量的回归系数在全局范围内未发生正负变化,如车速、年龄等变量的回归系数均为正值,这表明在全局范围内,这些变量对摩托车交通事故严重程度有正向影响。以车速为例,车速越快,摩托车交通事故严重程度会越严重。

2)另外一些变量,如逃逸、限速等变量的回归系数均为负值,这表明在全局范围内,这些变量对摩托车交通事故严重程度有负向影响。以驾驶员是否逃逸为例,若驾驶员逃逸,则驾驶员的受伤程度越轻,因为只有驾驶员未受伤或受伤程度较轻时才可能逃逸,驾驶员受伤程度严重的话则无法逃逸,回归结果与事实相符。

3)其余变量的回归系数在正负范围内均有分布,如:涉及车辆数、市区、疲劳等变量,表明这些变量对摩托车交通事故严重程度的影响随地理位置的变化呈现正向/负向作用。

4 多尺度异质性结果分析

4.1 尺度分析

空间尺度用带宽占总样本数量的比例来量化,带宽占总样本数量的比例越小,说明变量的空间尺度越小,则变量的空间异质性程度越大。传统GWR模型的带宽固定为8 278,体现的是各个自变量空间尺度的平均值。从表6可以看出:MGWR模型计算出不同变量的带宽,定量地反映了自变量的差异化空间尺度。

表6 MGWR模型带宽尺度

与驾驶员有关的变量中,疲劳驾驶的带宽为8 343,占总样本数量的45.1%;强光的带宽为6 861,占总样本数量的37.1%。

与车辆有关的变量中,车速的带宽为5 379,占总样本数量的29.1%;涉及车辆数的带宽为1 704,占总样本数量的9.2%。

与环境有关的变量中,市区的带宽为2 360,占总样本数量的12.8%;T型交叉口的带宽为3 612,占总样本数量的19.5%;夜间无灯光的带宽为5 682,占总样本数量的30.7%;多云的带宽为1 662,占总样本数量的9.0%。

上述变量的空间尺度均较小,说明这些变量的空间异质性程度较大。其余变量的空间尺度均较大,至少占总样本数量的50%以上,几乎属于全局尺度。

4.2 影响因素空间异质性分析

结合MGWR模型回归出的带宽与系数,对空间异质性程度较大的影响因素进行分析,用ARCGIS将影响因素的回归系数可视化,回归系数的正负值表示影响因素对摩托车交通事故严重程度具有正向/负向作用,系数均值的绝对值大小表示作用强度。影响因素的可视化结果见图2。

根据影响因素的回归系数空间分布图,从驾驶员、车辆和环境3个方面分析影响因素的空间异质性。

4.2.1 驾驶员因素

疲劳驾驶的回归系数分布见图2(a),回归系数范围为[-0.017,0.026],呈现正负差异,系数大小由白色点区域向黑色点区域递增。在深灰色点区域,疲劳驾驶会导致摩托车交通事故严重程度增加,因为疲劳驾驶会使驾驶员生理和心理功能下降,导致行驶过程中驾驶员的判断准确性降低。在白色点区域虽然驾驶员也是疲劳驾驶,但驾驶员受伤程度却减少,原因可能是在这些区域,相关部门采取了措施缓解了驾驶员的疲劳程度,如增设各种警示标志、强制休息等。系数均值的绝对值为0.006,作用强度最低。

驾驶员视线受外部强光影响的回归系数分布见图2(b),回归系数范围为[-0.039,0.035],呈现正负差异,系数由白色点区域向黑色点区域递增,但黑色点区域较小,集中分布在该州中部地区,说明在该州的绝大部分区域内,驾驶员受外界强光刺激时,摩托车交通事故严重程度减少,原因是驾驶员在受到强光刺激无法看清路面情况或前方车辆时,本能的会立即降低车速保证安全,从而降低驾驶员受伤严重程度。系数均值的绝对值为0.018,作用强度高于夜间无灯光。

4.2.2 车辆因素

车速的回归系数分布见图2(c),回归系数的范围为[0.234,0.348],系数均为正值,说明车速对摩托车交通事故严重程度是稳定的正向影响。即车速越快,驾驶员受伤越严重,该推断与实际情况相符。系数均值的绝对值为0.292,作用强度最大。

涉及车辆数的回归系数分布见图2(d),回归系数的范围为[-0.191,0.077],呈现正负差异,系数由白色点区域向黑色点区域递增。在该州的大部分区域,涉及车辆数与摩托车交通事故严重程度是负相关,仅在该州中部东侧沿海的小部分区域是正相关。原因是在该区域交通流量大,车辆数量多,容易发生多车相撞的交通事故,使驾驶员受到更严重的伤害,其余地区则相反。系数均值的绝对值为0.077,作用强度仅低于车速。

4.2.3 环境因素

事故发生在市区的回归系数分布见图2(e),回归系数的范围为[-0.259,0.041],呈现正负差异,系数由白色点区域向黑色点区域递增。在黑色点区域地区,事故发生在市区会使驾驶员遭受更严重的伤害,因为市区环境和交通组成复杂,人流量和车流量比郊区更大。而在其余区域,事故发生在郊区会增加摩托车交通事故严重程度,因为郊区车流量较少,驾驶员容易发生超速等违规行为,导致摩托车交通事故严重程度增加。系数均值的绝对值为0.053,作用强度低于涉及车辆数。

T型交叉口的回归系数分布见图2(f),回归系数的范围为[0.005,0.091],系数均为正值,说明T型交叉口对摩托车交通事故严重程度是稳定的正向影响,即在T型交叉口处发生事故时驾驶员会受到更严重的伤害。因为T型交叉口一般设置在较偏僻的路段,用于搭接支路,在车流量不大的情况下往往不设置信号灯,导致行车方式会比普通路口更随意,从而造成更严重的交通事故。系数均值的绝对值为0.051,作用强度低于市区。

夜间无灯光的回归系数分布见图2(g),回归系数的范围为[-0.034,0.045],呈现正负差异,系数由白色点区域向黑色点区域递增。黑色点区域的系数为正,说明在该州的大部分区域,夜间无灯光的环境下会导致摩托车交通事故严重程度增加,因为驾驶员在黑暗环境下,摩托车自身灯光照明范围有限,驾驶员无法看清路面或周边情况,出现意外状况时无法及时做出正确反应。白色点区域系数为负,集中分布在该州的东北角区域和东南角沿海区域,说明在该区域,夜间无灯光的情况会降低摩托车交通事故严重程度,原因可能是在该区域,相关部门在路侧增设了警示警告标志,并设置了保护措施,驾驶员主动降低车速、保持警惕,提高了安全水平。系数均值的绝对值为0.013,作用强度高于疲劳驾驶。

多云天气的回归系数分布如图2(h),回归系数的范围为[-0.046,0.146], 呈现正负差异,系数由白色点区域向黑色点区域递增。白色点区域集中在该州的中部和南部少数区域,该州大部分区域的系数为正,说明在多云天气的条件下,大部分区域发生交通事故时摩托车交通事故严重程度会增加。因此相关部门应该在多云天气时,利用多种方式提醒驾驶员行车过程中注意安全。系数均值的绝对值为0.048,作用强度高于强光。

5 结 语

1)MGWR模型在传统GWR模型上增加了尺度的计算,通过分析不同解释变量的空间尺度差异,定量反映了各因素对摩托车交通事故严重程度的空间异质性程度。

2)在全局尺度的影响因素中,驾驶员逃逸、道路限速、单向行驶道路等因素对摩托车交通事故严重程度是负向影响,弯道、未戴头盔、生病等因素对摩托车交通事故严重程度是正向影响,同时这些因素的空间异质性程度较小。

3)在空间异质性程度较大的影响因素中,变量多云的空间尺度最小,其空间异质性程度最大,其他影响因素按空间异质性程度从大到小分别为:涉及车辆数、市区、T型交叉口、车速、夜间无灯光、强光、疲劳;同时,变量车速的系数均值绝对值最大,其作用强度最大,其他影响因素按作用强度从大到小依次为:涉及车辆数、市区、T型交叉口、多云、强光、夜间无灯光、疲劳。

4)在研究交通事故影响因素的异质性时,只考虑了空间异质性,未考虑时间的非平稳性,综合时间不稳定性与空间异质性分析是今后研究的方向之一。

笔者采用了国外的摩托车交通事故数据进行了研究,虽然我国交通情况较国外有一定的特殊性,但从发达国家的摩托车交通事故中吸取经验教训是有价值的。首先国内的交通事故数据在记录时可以进一步丰富交通事故数据的内容;其次,摩托车交通事故严重程度的影响因素存在空间异质性,后续研究如何将国内不同区域的特征作为影响因素纳入模型考虑,构建更符合国内情况的空间模型,是进一步研究方向;最后,因为摩托车交通事故的影响因素具有空间异质性,相关部门在制定交通安全策略时,应根据不同区域的情况因地制宜地制定。