高桩承台基础波流荷载数值模拟
楚晨晖,陈少林,张洪翔
(1.无锡环境科学与工程研究中心,江苏 无锡 214100;2.南京航空航天大学 土木与机场工程系,江苏 南京 211100;3.中国能源建设集团湖南省电力设计院有限公司,湖南 长沙 410000)
跨海桥梁处于海洋环境中,浪、流荷载是其重要的控制荷载。海洋环境多变复杂,近海地区台风、巨浪等极端气候多有发生。历史上曾多次发生飓风引发极端浪潮对桥梁结构造成严重破坏的事故[1]。跨海大桥的桥墩、承台及桩基础长期受到波浪及水流荷载冲击,受力复杂[2-3]。因此,深入研究波流对桥梁基础的荷载作用具有重要的理论意义和工程价值。工程实践中,目前中、美、英等国的规范均采用基于Morison 小尺度水工结构水平力计算公式[4]。Morison 方程是一个半经验、半解析的简化计算式,当特征尺寸与入射波长之比小于0.2 时,计算精度基本满足工程需要[5]。对于大尺度结构,由于构筑物与波浪场的相互耦合干扰,会产生复杂的绕射、反射效应,采用Morison 方程计算波浪力往往会高估结构所受的荷载[6]。跨海大桥桥墩、基础等属于典型的大尺度构筑物。针对大尺度构筑物波浪力的研究,Maccamy 等[7]基于势流理论首先提出了线性绕射理论计算大尺度圆柱波浪力,后人不断对势流理论和绕射理论进行补充和完善[8-11]。物理水槽试验是研究水动力学的重要手段,兰雅梅[12]采用水槽试验方法对规则波作用于承台及单桩的水动力特性开展研究,得到了冲击压强随承台相对净空及相对长度的变化规律,讨论了承台对桩柱的水动力影响;魏凯等[13]进行了极端波浪冲击高桩承台的水槽试验,基于试验数据建立了波浪冲击荷载时程模型,并基于Copula 理论,建立了荷载上升段和峰值段的联合概率模型。随着计算机技术和计算流体力学(CFD)理论的发展,数值模拟试验被广泛应用于波流荷载的研究。仇正中等[14]基于三维势流理论,采用流体动力学软件SESAM,对某大桥主桥墩承台基础波浪荷载展开研究,计算不同波浪周期、承台吃水、浪向角情况下的承台荷载,分析承台波浪荷载的变化规律,研究认为实际施工中承台吃水和波浪荷载近似呈线性关系,需考虑约15%的安全系数;刘正浩等[15]应用自主研发的CFD 求解器,对不同水深工况下的固定式高桩承台风机基础的水动力参数进行数值模拟,研究发现水深对风机基础水平向的受力影响不大,但对砰击压力的影响很大,水深越深,风机基础受到的砰击压力越大,波高对风机基础的受力影响很大,波高越大,观察到的波浪破碎现象越严重。
多数学者的研究对象聚焦于桥梁基础在波浪作用下的整体受力趋势[16-19],而对其表面的压力分布关注较少。掌握承台-桩基表面压力分布规律,可以优化结构设计。另外,桥梁基础波浪荷载来自于波浪的冲击惯性力及流体压差,波浪和结构相互作用时,一般将结构视为刚体模型,而波浪冲击结构时,波浪会产生越浪、绕射等效应,扭曲变形的波浪反作用于结构。因此,结合波浪荷载时程,研究波浪与结构相互作用时形态变化有助于更全面深入地了解波浪荷载的形成机理。然而,解析计算方法仅适用于规则的桩柱结构,物理水槽试验方法能够较为客观地反映结构整体受力情况,但限于测点布置数量及布置测点本身对结构表面的影响,使得物理试验很难完整真实地描述复杂结构的表面压力分布。同时,试验方法也不便于追踪和记录水质点的即时波高。数值模拟方法可以很好地描述复杂桥梁基础的表面压力分布,能够记录波浪场中任意时刻任意质点的即时波高,进而描述波浪冲击基础时的形态变化。
基于上述分析,拟开展某跨海大桥高桩承台复合基础的波流荷载数值模拟。首先,通过网格比选进行模拟试算,将计算所得水动力参数与已有物理水槽试验数据进行对比,验证数值模拟的准确性;然后改变初始静水面标高,计算不同淹没系数下的高桩承台复合基础的水平力、浮托力;进一步研究典型周期内波流冲击复合基础各阶段的波浪形态,分析讨论承台及桩基的压力分布规律。
1 控制方程及数值水池造波方法
1.1 RANS 法控制方程
采用不可压缩流体运动的三维雷诺时均方程,RANS 法的连续方程为:
式中:u、v、w分别为流体在x、y、z方向的速度(m/s)。
考虑到出口处波浪反射会对计算域内流场产生干扰,故在出口1~2 倍波长范围内设置消波区。采用源项消波方法,在消波区范围内设置阻尼消波项。添加消波源项后的动量方程如下:
式中:ui、uj为i、j坐标方向的流体运动时均化速度;t为时间;ρ为流体密度,取998 kg/m3;p为流体压强;gz为竖向重力加速度,取9.8 m/s2;υ为运动黏度,取1.006×10-6m2/s;为雷诺时均应力;νt=ρCµk2/ε定义为湍流速度;δij为“Kronecker delta”符号,即当i=j时,δij=1;当i≠j时,δij=0;k、ε分别为湍动能和湍动能耗散率;α为消波经验系数;x1、x2分别为波流传播方向的消波区起始点和结束点的坐标值。
1.2 数值水池造波方法
将速度及体积分数变化函数编写UDF 语言并设置为入口的边界条件。根据Stokes 波浪理论进行数值模拟造波。选用Stokes 二阶波模型造波,其任意时刻的波面函数及势函数分别为:
式中:H为波高;T为周期;L为 波长;h为 水深;z为 即时波高;k=2π/L,ω=2π/T。
对势函数求导即可得到水平向和竖向的波浪传播速度:
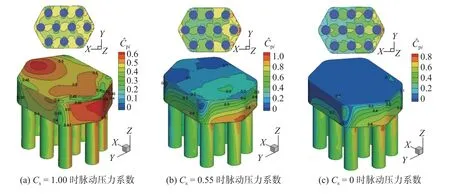
采用VOF 方法对液面变化进行模拟跟踪。其主要思路是:假设每个控制体积多相体积分数总和为1,每个控制容积第一相体积含量为aq,若aq=1,表示控制体积内只含有第一相,若aq=0,表示控制体积内不含第一相,若0 式中:n为当前计算时间步;ρq为第q相的物理密度;表 示从第p相到q相的传质;Saq为源项;V为单元体积;Uf为通过单元截面的体积通量;aqf为第q相体积分数的单元界面值。表示控制体的净通量,即通过各个单元面法向方向的质量通量之和。 以某跨海大桥主桥墩承台-桩基础为研究对象,该桥墩基础为10 桩配6 棱承台结构形式,其具体尺寸见图1。为方便表示不同水位高度条件,定义无量纲承台淹没系数: 图1 桥墩基础示意(单位:m)Fig.1 Pier foundation (unit: m) 式中:Cs为承台淹没系数;H0为 静水面至承台下表面垂直高度(m);D为承台厚度(m)。 根据淹没系数,分别定义百年一遇水位、常年平均水位及静水面与承台底齐平时对应水位的3 种工况,如图1(b)所示。波浪要素及工况条件如表1 所示。 表1 波浪要素及计算工况Tab.1 Wave elements and working conditions 为保证模拟计算准确性,需进行网格无关性检验。计算域范围:长度取近似6 倍波长600 m,高度取40 m;宽度取120 m。在出口前2 倍波长处设置消波区。桥墩底面中心设置在距入口处约2 倍波长(200 m)处。整体计算域采用混合网格单元,约1 个波高范围内(7 m)网格加密,布置20 个单元,高0.35 m。在桥墩附近采用局部加密的非结构化网格,尺寸为40 m×40 m×25 m,桥墩表面网格加密。加密区以外计算域采用结构化网格,控制入口处最大网格尺寸,入口至加密区网格均匀分布。由于消波区至出口处不是重点考察对象,故出口处网格尺寸适当加大,加密区至出口范围网格按指数率分布。采用k-ε realizable 湍流计算模型,离散方程求解采用PISO 格式。VOF方程采用显式差分格式求解,时间步长0.005 s,迭代计算过程库朗数控制在0.5 以下。计算域、边界条件及网格划分见图2。为验证网格无关性,设计6 组网格方案进行试算,网格尺寸如表2 所示。 表2 不同网格方案参数Tab.2 Parameters of different grid schemes 图2 计算域尺寸、边界条件及计算网格Fig.2 Calculation domain size and boundary condition computation grid 以某物模缩尺水槽试验为参考[20],验证数值模拟合理性。试验水槽长50 m,宽7 m,高1.2 m。根据《波浪模型试验规程》,试验模型几何比尺为λl=50,根据弗劳德相似准则,流速、时间、压强比尺及总力比尺分别为7.07、7.07、50 及125 000。 试验中在承台顶安装4 个总力仪,以同步测定竖向浮托力;在承台的侧端与末端各安装 1 个总力仪,以测定承台及桩基在水平方向上纵向与横向的总力;在承台前端布置3 个压强点,以测定承台迎水面水平压强;在承台底部布置4 个压强点,以测定承台底部的压强;除桥墩完成整体测力外,还将桥墩的承台与桩基进行分割,保持桩基位置不变,承台略往上抬保证其不与桩基接触,以便单独测量桩基测点压强及水平总力。试验测点布置及试验过程如图3 和4 所示。 图3 模型测点布置Fig.3 Layout of model measuring points 图4 物模缩尺水槽试验Fig.4 Flume experiment process 水槽试验测量及数值模拟计算结果见表3。由表3、图5 可知,网格方案3~6 的水平荷载计算值趋于一致,即水平向荷载对网格敏感性较低;而竖向浮托力对网格敏感性较高,当网格尺寸加密至方案5 后,数值模拟结果基本收敛于试验值。分析说明采用网格方案5 基本能达到数值模拟精度。 表3 Cs=1.00 计算结果对比Tab.3 Comparison of calculation results (Cs=1.00) 单位:kN 图5 Cs=1.00 工况下采用不同网格方案的计算值与试验值对比Fig.5 Comparison of calculation results and test results of different schemes (Cs=1.00) 为进一步验证网格方案选取的合理性和数值模拟的计算精度,利用网格方案5,仅改变波高加密区范围,计算Cs=0.55 工况对应的桩-承台表面压力。由图6 可见,典型参数计算值的相对误差均控制在10%以内。综上可知,采用网格方案5 能够兼顾计算效率和计算精度。 图6 Cs=0.55 工况下采用网格方案5 计算数据与试验值的对比Fig.6 Comparison between calculation results of grid scheme 5 and test results (Cs=0.55) 为研究波流作用下的桩-承台压力时程特性,定义各压力荷载无量纲参数。承台水平力系数、承台浮托力系数及群桩总力系数分别定义如下: 式中:Ctx为无量纲承台水平力系数;Ftx为承台所受波流水平力;H为波高;b为 承台宽;h为 水深;Ctz为无量纲承台浮托力系数;Ftz为承台所受波流浮托力;A为 承台底面积;Fpi为单桩所受波流水平力;Cp为群桩总力系数;D为桩基直径。以上参数中下标含义:t 为承台;p 为桩基;x、z为荷载方向,分别表示沿波传播水平方向和竖直方向。 图7、图8 给出了3 个完整周期内(t/T=1~3)承台水平压力系数和竖向浮托力系数的时程曲线。从图7 可知,随着淹没系数的降低,正负向水平荷载也逐渐降低;峰值到达时间逐渐延后。当静水面处于承台底面以上时,正向荷载峰值过后产生明显的负向水平冲击力;而当淹没系数为零时,负向冲击效应逐渐减弱。图8 显示了竖向浮托力的时程变化特征。与水平压力相反,随着淹没系数的降低,承台竖向浮托力随之增大,峰值到达时间同样延后。淹没系数大于0 时,竖向浮托力在主峰值过后又产生1 个次峰值,随着淹没系数减小至0,次峰值趋于平缓。当淹没系数为0 时,可以观察到浮托力主峰值具有1~2 次明显的脉冲效应,冲击时间短,冲击力强。浮托力峰值过后,反向浮托力冲击效应亦趋于平缓。 图7 不同工况下承台水平力时程Fig.7 Horizontal force time history of bearing platform under different working conditions 图8 不同工况下承台浮托力时程Fig.8 Buoyancy time history of bearing platform under different working conditions 群桩总水平时程曲线如图9 所示。与承台浮托力时程相似,随着淹没系数降低,群桩总力系数增大,且当Cs=0 时,群桩总力系数远大于承台淹没水中工况。由图9 可知,群桩水平力总力系数的峰值过后,与Cs>0 时曲线平稳下降有所不同,Cs=0 时,在波谷附近产生明显的荷载波动。 图9 不同工况下群桩总水平力时程Fig.9 Total horizontal force time history of pile group under different working conditions 为考察在群桩总力最大状态下各单桩水平力分配情况,定义单桩贡献系数: 取典型周期(t/T=1~3)内的群桩总力时程进行分析,其正向、负向最大力下的各单桩贡献系数如图10 所示。可见,在群桩正向总力达到最大值时,3 种工况下的Z3(Z10)单桩贡献系数均最大,当Cs=0 时,Z1 贡献系数增大,而Z7 贡献系数则明显减小;当群桩负向总力达到最大值时,中间一排桩(Z4~Z7)存在明显的越靠后排贡献系数越大的规律,且Z7 贡献系数明显大于其他位置桩,随着水位下降,其值明显增大。由此可见负向最大值主要来自于Z7 承受的反向波流冲击。 图10 群桩总力正向(负向)最大时各单桩贡献系数Fig.10 Contribution coefficient of each single pile when the positive force (negative force) is maximum 图11~13 给出了3 种工况下,水平荷载由峰值至谷值各时刻波浪形态历程。由图11 可见,当Cs=1.00 时,越浪现象明显,波浪传播过程中较完整,未被击碎,承台对波浪的阻挡效应较弱。正向水平力达到峰值前,浪潮头已越过结构,波浪拍击效应较弱,承台整体处于波浪液面以下。由此可见,此时水平力峰值来自浪流联合作用。波浪完全越过承台后,在尾流区产生明显的绕射波浪,与正向波浪汇聚形成水流向上脉冲现象,反向波浪与正向波浪合力作用在承台底面,产生了竖向浮托力二次峰值。由图12 可见,Cs=0.55 时,波浪没有完全越过承台结构,当波峰冲击承台正面时,形成正向水平力峰值;波浪完全越过承台后,发展出紊乱无序的绕射波浪,导致负向水平力的波动变化。由图13 可见,Cs=0 时,波浪与承台正向有明显的冲击拍打现象,说明水平力峰值持续时间极短。此外,观察图13(e)可知,Cs=0 时,波浪越过承台后,尾流区没有明显的绕射波浪,以至于承台的反向冲击效应不明显。 图12 Cs=0.55 时波浪形态时间历程(单位: m)Fig.12 Time history of wave form (C s=0.55) (unit: m) 图13 C s=0 时波浪形态时间历程(单位: m)Fig.13 Time history of wave form (C s=0) (unit: m) 对比3 种工况波浪形态时程图,可以总结出高桩承台基础的波浪荷载形成机理:(1)当淹没系数较大时,波浪的拍击效应较弱,承台压力峰值主要来自浪流联合作用;(2)随着水位降低,水平力峰值的脉冲效应逐渐明显,由于承台淹没系数的降低,水流对承台作用降低,荷载以波浪拍击力为主;(3)结构尾流区会形成绕射波浪,且绕射效应随淹没系数增大而增强,绕射波浪会产生负向水平力和负向浮托力;(4)随着淹没水位降低,直至波面直接与群桩接触,波浪传播中被群桩干扰阻碍形成破碎波,致使群桩总力、单桩水平力的时程变化波动剧烈。 为研究承台在不同工况波浪作用下的压力分布,定义平均压力系数及承台脉动压力系数: 图14 给出了不同工况下的承台、桩基平均压力分布三维视图(下)和承台俯视图(上)。可见,承台及桩基平均压力分布明显与初始水位有关,即结构位置所处水位以下越深,所受平均水压越大。同深度迎波面桩基压力明显大于背波面。进一步观察发现,在同高度范围内,承台侧面转角处平均压力明显低于相邻竖侧面。结合图11~13 分析可知,波浪传播时会被承台阻碍形成“劈波效应”,波浪沿承台转角处分散传播,导致转角处受波浪冲击效应低于周围侧面。图14(c)显示转角附近平均压力趋于0,结合图13(b)可知:随着淹没系数的降低,承台“劈波效应”更加明显。 图14 平均压力系数分布Fig.14 Distribution of average pressure coefficient 图15 显示了承台及桩基表面压力波动情况。当Cs=1.00 时,承台前迎波面和顶面尾部两处有明显的脉动压力系数极值区,随着淹没系数的降低,脉动压力系数极值区域不断缩小直至消失,因为迎波面压力波动是由波浪周期性正面冲击承台形成的。结合图11 可知,Cs=1.00 时顶面压力波动是由绕射波浪与正向波浪汇聚冲击而形成。随着淹没系数的降低,越浪效应减弱,致使顶面压力波动减弱。Cs=0 时,波浪未越过承台结构,拍击承台正面后被分离成破碎波向两侧传播,承台顶面未受水压作用,因此顶面压力脉动系数几乎无变化。继续观察承台底面脉动压力系数分布,可以看出几种工况下,承台底面沿X方向桩列和桩间脉动效应差异明显,即随着淹没系数的增加,前后方向脉动压力系数存在明显梯度,桩列的“阻挡效应”和“劈波效应”也显著增强。 图15 脉动压力系数分布Fig.15 Distribution of fluctuating pressure coefficient 为研究高桩承台基础在波流作用下的荷载时程特性及压力分布规律,采用RANS 方法对某跨海大桥高桩承台基础进行数值模拟研究,得到以下结论: (1)承台水平力随淹没系数增加而增加,承台浮托力、群桩水平力随淹没系数增加而降低。 (2)群桩正向总力最大时,迎波方向的边列最后排桩基受力最大;群桩负向总力最大时,迎波方向中间列桩存在明显的越靠后排贡献系数越大的规律,且中间列最后排桩在群桩中受力最大。 (3)淹没系数较大时,承台压力峰值主要来自于浪流共同作用,结构尾流区会形成绕射波浪,绕射波浪会产生负向水平力和负向浮托力。随着淹没系数的降低,承台对波浪的“劈波效应”增强,水平力峰值的脉冲效应明显,水流作用影响减弱。波浪传播中被群桩干扰阻碍形成破碎波,致使群桩总力、单桩水平力的时程变化波动剧烈。 (4)由于“劈波效应”,使得承台棱角部分平均压力低于附近侧面。初始静水面与承台顶平齐时,承台正前方和顶部后方会产生波动极值区域,并随着静水位降低而逐渐减小并消失。2 模型建立及验证
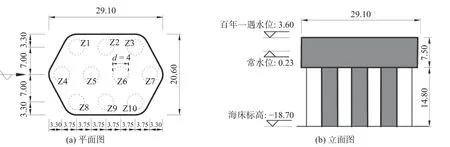


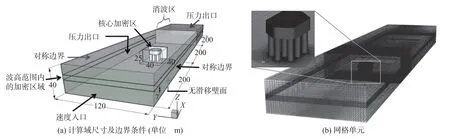



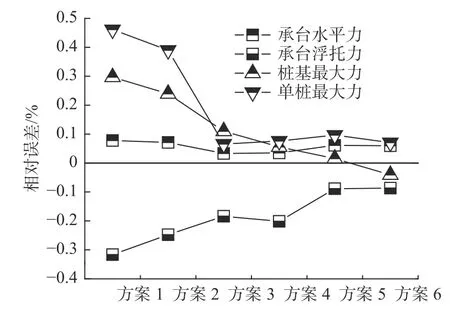

3 波流作用下桩-承台压力时程分析




4 波浪形态时程及波浪荷载形成机理
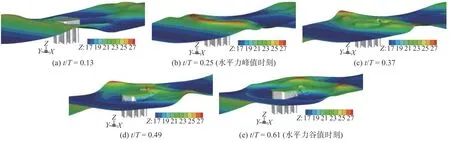

5 波流作用下桩-承台压力分布特性

6 结语

