指向计算思维的Python编程教学项目设计——以“数值计算”为例

宋敏毅 江苏省天一中学

《普通高中信息技术课程标准（2017年版）》将计算思维列为信息技术学科四大核心素养之一，并指出：具备计算思维的学生在信息活动中能够采用计算机可以处理的方式界定问题、抽象特征、建立结构模型、合理组织数据；通过判断、分析与综合各种信息资源，运用合理的算法形成解决问题的方案；总结利用计算机解决问题的过程与方法，并迁移到与之相关的其他问题解决中。

因此，笔者将教科版高中信息技术必修一第四单元第二节“数值计算”的拓展练习内容与选修教材《算法初步》中算法应用模块知识点相结合，设计了相应的教学项目，并将整个教学设计的思路总结为情境创设、初步探究、项目优化、项目总结四个阶段，进而培养学生的问题解决与方案优化能力，发展其计算思维。

●情境创设

情境创设是为了更好地激发学生的好奇心和求知欲，使学生主动地参与到项目学习中，从而提升教学效率。因此，教师需要充分了解学生的年龄特点、知识基础、认知水平以及学生的日常生活，并根据以上信息分析学生的普遍兴趣点，以兴趣点为基础扩散思维，争取为学生设计出更加生动、引人入胜的教学情境。

例如，根据必修一第四单元第二节“数值计算”的拓展练习内容，以及选修教材《算法初步》中算法应用模块的内容，笔者选择了最大公约数问题作为项目的驱动问题。在课前先展示一道比较简单的求解两个正整数的最大公约数的问题——20和8的最大公约数是多少，并在学生回答问题的时候设计了体现信息素养或提升趣味性的问答环节，如利用Python程序随机选择学生或击鼓传花等小游戏。在揭晓答案后，引导学生复习最大公约数的计算方法——穷举法、短除法、分解质因数法、辗转相除法等。接着，布置一道位数较多较复杂的正整数之间求解最大公约数的问题，如“9147485和5147480的最大公约数是多少”，要求学生利用计算机程序来解决。最后，提出项目学习目标——计算两个正整数的最大公约数。

●初步探究

项目初步探究主要是在学生明确项目学习目标后，初步选择一种方法尝试解决问题。在本项目中，在设计解决“9147485和5147480的最大公约数是多少”这一问题的算法时，一定要以学生为主导，教师仅起到辅助学习的作用。

教师首先带领学生回忆算法的概念与特征，并让学生在求解最大公约数的四种方法中选择较好理解且容易转换为Python程序代码的方法。其中，穷举法最能体现计算机解决问题的常规思路，因为计算机可以不知疲倦地进行穷举计算。穷举法的另一个优势是算法思路简单易懂，只要通过穷举尝试所有可能的数，并找出最大的那个约数即可。手工计算非常复杂，但通过运行程序，学生会发现利用计算机程序来解决该问题难度就变小了。

在为学生介绍穷举法的思路后，就可以让学生尝试将其转换为Python代码，从而解决“9147485和5147480的最大公约数是多少”这一问题。教师可以提出用for循环或者while循环来实现，图1展示了一种基于while循环的样例程序。在这一阶段的项目任务单中，教师可提供while循环和for循环的相关信息让学生参考，还可组织小组交流讨论等学习活动让同学们集思广益，明晰穷举法算法设计的思路。

图1 穷举法代码

●项目优化

项目优化主要是在项目初步探究的基础上对解决方案进行剖析，进一步探究更便捷、高效的解决方案，或者在初步方案的基础上优化解决方案。在本项目中的项目优化则是指向基于同一问题选择更高效的方法设计代码，最直观优化的指标就是算法的复杂度。

算法的时间复杂度是指执行算法所需要的计算工作量，可以用算法执行的基本运算次数度量；算法的空间复杂度是指执行算法需要的内存空间，包括算法程序、输入的初始数据以及算法执行过程中需要的额外空间。以上两个知识点均在高中信息技术选修教材《算法初步》中有所涉及，运用于此也可以体现该教学项目中的知识框架是由“数值计算”与“算法作用”两大知识点联合构造。

在设计出穷举法的算法后，学生已经可以计算出9147485和5147480的最大公约数是5。接着，教师让学生将两个正整数的位数再增加一些，如增加至十位，学生就会发现代码需要很长时间才能运行结束，甚至一直没有结果。这样学生就会明白穷举法虽然能够解决问题，但只有在数字较小的情况下才具有较好的实用性和可行性。

接着，引导学生在选择解决问题方法这一层面优化算法，使算法的通用性更高、时间复杂度更低。这时，教师可以带领学生回忆最大公约数的计算方法——穷举法、短除法、分解质因数法、辗转相除法。其中，辗转相除法最著名，且思路较为清晰，方便学生进行编程。这个阶段就可以让学生上网搜索辗转相除法的相关信息，并将其算法以流程图的形式呈现。图2是辗转相除法的流程图样例，当学生完成流程图后，先让其分享讨论，教师再点评。接着，学生根据流程图编程，并用较大的数字进行测试，感受该算法的计算效率，同时，教师要在学生完成代码的过程中给予帮助，图3为参考代码。

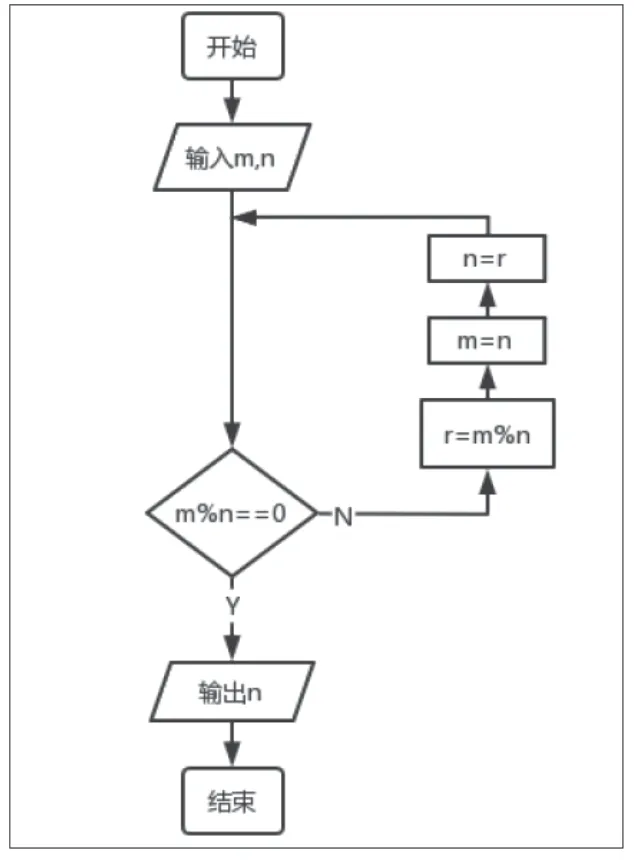
图2 辗转相除法流程图

图3 辗转相除法代码

●项目总结

在项目实施过程中，在将辗转相除法转换为Python程序代码后，教师引导学生比较两种算法的区别，并分别从以下指标来评价两种算法：正确性、可读性、健壮性、运行效率、通用性、时间复杂度。这时，教师可以在项目任务单上给出比较表格供学生探究后填写（如右表），并在本阶段给出各个指标的含义或计算方法。

正确性是指代码可以正确输出结果，能解决对应的问题。

可读性是指代码容易理解，容易编程和调试，容易维护。

健壮性是指系统在不正常输入或不正常外部环境下仍能够表现正常的程度，即尽可能地设计容错机制。

运行效率是指计算相同问题时两个代码的时间消耗的比较，时间消耗少的运行效率高，反之则低。

通用性是指算法能否解决这一类问题中的所有情况，解决的情况越多通用性越高。

时间复杂度这一项，可以结合选修教材《算法初步》给出复杂度的计算方法，让学生自行探索并计算两个算法的时间复杂度。由于辗转相除法的时间复杂度计算有一定难度，可以利用网上的视频或者相关材料帮助学生理解。

算法特性对比表

其中，为了更直观地比较两种代码在解决同一问题时的运行时间，教师可以向学生引入time库的函数，用于记录程序运行的时间。可以在代码起始处import time即引入time库，而后在用户输入两个正整数的代码后，添加start=time.time()代码用于记录开始时间，在输出公约数的代码后添加t=time.time()-start代码计算程序运行时间。最后，利用输出语句把运行时间输出，即可直观地看出两种算法的代码运行时间。

在学生比较了两种算法的各项指标后，他们会发现不同的算法区别很大，并理解解决同一个问题存在不同的算法，且算法存在有效（无效）、高效（低效）等差别。在本阶段，教师可以基于以上项目目标和标准发放自评、小组互评的问卷，个性化地了解每位学生的项目实施情况以及计算思维能力的提高。

●结语

本项目融合教科版高中信息技术的“数值计算”和“算法应用”两模块知识点展开教学设计，提升了学生解决问题和优化解决方案的能力。在项目实践中，自主探究和小组协作讨论激发了学生主观能动性，提升了学生的学习效率。

在高中信息技术教材中，还有很多内容适合使用项目驱动的方式来进行整合，它一方面可以将编程内容与数学等相关学科的知识点融合，另一方面也可以把不同章节的内容通过同一个项目来融合。