从自动计算的可行性看数据与表征

陈凯 上海市位育中学

0这个数字可能有很多含义，有时候用来代表没有，有时候用来代表正数和负数交界的那个特殊的数字，在很多程序语言中，0这个数字代表布尔值的“假”，但有时候也用来代表函数运行成功。人们可以在头脑中轻松地进行0*x这样的数学运算，或者0andx这样的逻辑运算，当然，用计算机也可以轻松地做到这些，但这种轻松掩盖了事情背后的实际情况。若将当前的计算机拆解至晶体管那样细小的程度，尽管复杂，还是能够观察到机器是如何将某种低电压作为0、高电压作为1（或者其他对应方式）从而控制开关电路实现信号的传递和计算的——相对而言，倒是人头脑内部的工作情况更难以直观地显现出来。周以真说，“计算思维是人的思维方式而不是计算机的思维方式”，“计算思维是思想，不是人造物。不只是我们生产的软件硬件等人造物将以物理形式到处呈现并时时刻刻触及我们的生活，更重要的是还将有我们用以接近和求解问题、管理日常生活、与他人交流和互动的计算概念”[1]，对这些话的理解也许会产生分歧，但笔者从中得到一个重要的启发，就是在求解问题的过程中，可以先将以物理形式的时时刻刻触及我们的软硬件人造物——这个人造物基本上就是人们日常使用的计算机——先行排除出去，而将目光放置在计算得以实现的概念上。在周以真的原文中，“计算概念”一词是“computational concepts”，指的是与计算机有关的诸多概念，这提示了求解问题过程中概念先行的重要性。本文围绕二进制编码的数据与数据的表征方式，从概念出发对求解问题的计算装置进行设计和创造，讨论将这样的过程用于信息技术教学的可能性。

●交替转向行为与计算

这里给出一个稍微有点奇怪的例子，有一种甲壳动物名为鼠妇，除了平时喜欢生活在阴暗潮湿的地方，它还有一种有趣的习性叫做交替转向行为，如当它行走时遇见障碍，就向右转弯，又遇到障碍，就向左转弯，再遇到障碍，就向右转弯… …如此左右交替。

这种基于条件的行为的变化提示了将其用于计算的可能性，与计算机有关的二进制编码数据与表征的概念，恰好对应了鼠妇行走过程中要么这样、要么那样的二分选择行为。例如，可以将鼠妇向左转表示数据0，向右转表示数据1；或者，将没有障碍表示数据0，有障碍表示数据1；或者，将鼠妇无法到达目的地作为0，能够到达目的地作为1。以二进制解码器为例，假设输入两位二进制数，则需要输出相对应的0、1、2、3这4个十进制数字，在设计装置之前，就需要思考如何实现对数据的表征。输入部分相对容易处理，因为数据可以和鼠妇行为的两种状态进行直接对应；输出部分则比较困难，因为需要找到对应两位二进制数的4个数字的4种状态。

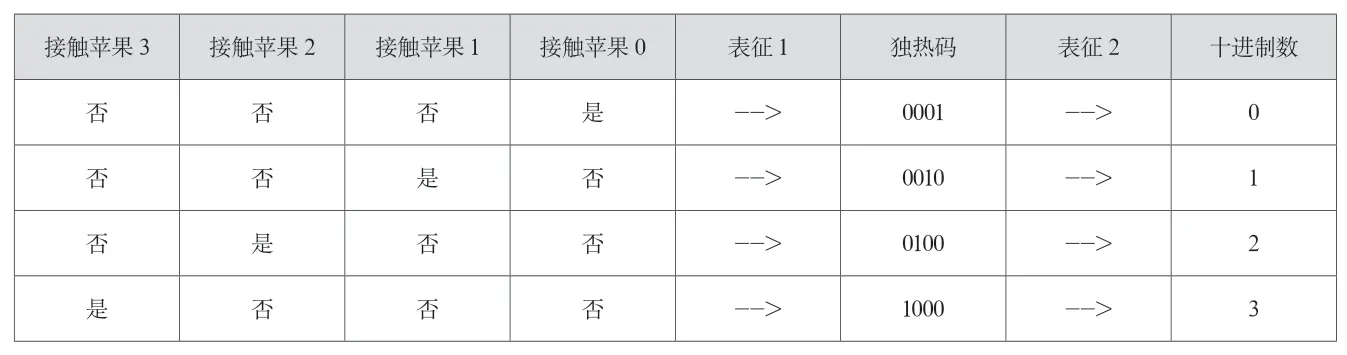
图1展示了一种设计方案：用积木挡板建造一个“迷宫”，将鼠妇放置其中，在迷宫中，标为B的挡板表示二进制数的第一位（低位），标为A的挡板表示二进制数的第二位（高位），挡板撤走代表数字0，挡板放下代表数字1，这样，鼠妇最终行走的方向就可以用来指示两位二进制数所代表的4个不同的数字。由于鼠妇在不同环境中的行走路径不同，可以在“迷宫”周围放置若干个“苹果”标记，通过观察鼠妇触碰到哪个苹果来获知计算的结果，如图2所示。在现实中，生物的这种强迫性的交替转向行为因各种因素的影响，是存在一定出错概率的[2]，这里假设鼠妇会以一种理想的状态严格遵守交替转向的行为规则。为了让鼠妇的行动更直观地显现出来，可以编写一个简单的程序来进行模拟。

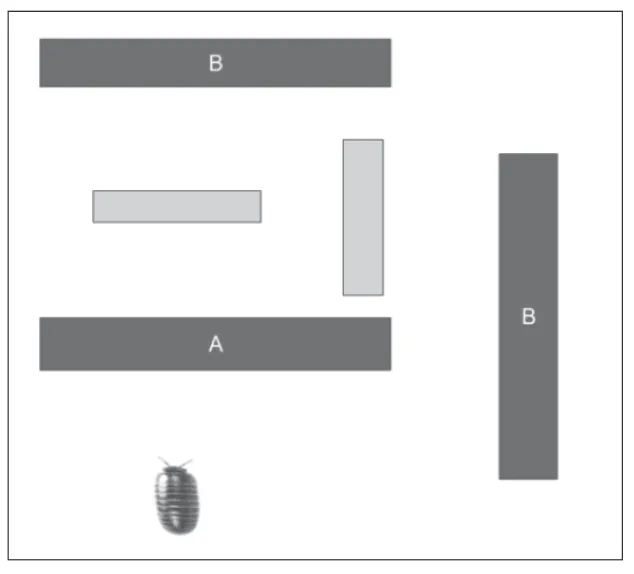
图1 初始状态下的挡板和鼠妇

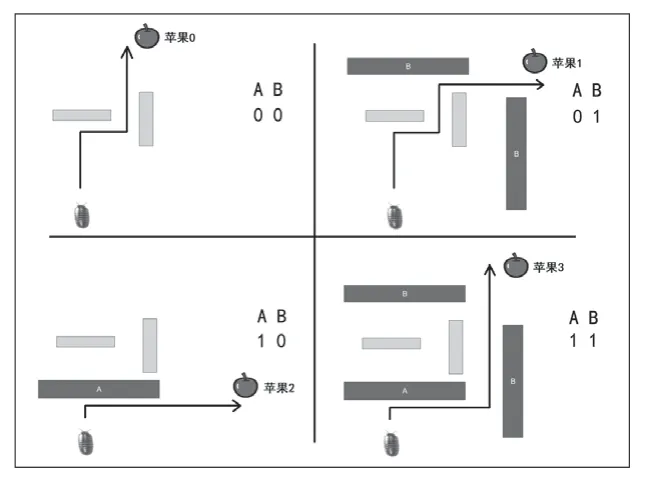
图2 对应两位二进制数4种情况的鼠妇行走路径

上面的例子是用两块挡板的有和无代表两个二进制数1或0，来实现二进制解码运算。其实，也很容易借助类似的方法来实现逻辑运算。与逻辑运算和或逻辑运算装置的设计

都非常容易实现，这里就不占用篇幅介绍了。相对难一些的是异或逻辑运算，其装置构造仿佛一种智力游戏，图3给出一种可行的设计：当挡板A或挡板B其中之一被撤除后，鼠妇就能走到苹果的位置，表示结果为1；当两块挡板都保留或都被撤除后，鼠妇就无法走到苹果的位置，表示结果为0，这样，鼠妇在走迷宫的过程中就实现了异或运算。接下来还可以进一步加以扩展，将异或运算和与运算结合起来，实现一个二进制加法装置，如图4所示。

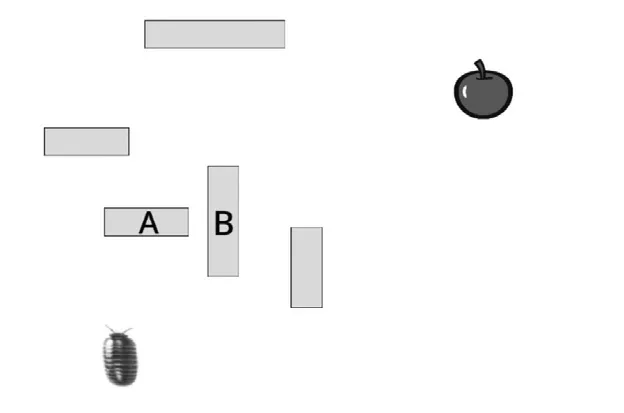
图3 一种异或逻辑运算的设计

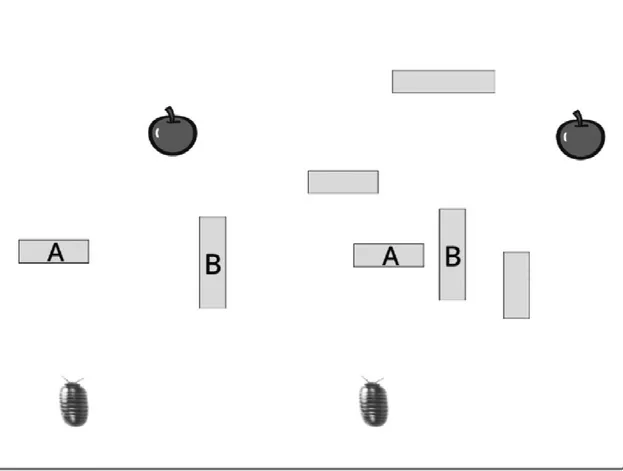
图4 一种加法运算装置的设计

●鼠妇计算装置中的数据和表征

仔细分析二进制编码数据与表征，就可以发现存在多种不同的情况：可以用二进制数据表征某个十进制的数据，如二进制数101表示存在5块积木挡板；或者用二进制编码的数据来表征特定的事物状态，如某个位置有积木挡板，可以用数字1表示，某个位置没有积木挡板，可以用数字0表示。本文给出的例子恰恰是反过来的，在计算的输入过程中，用有积木挡板来代表1，没有积木挡板来表示0。

可以发现，输出部分的表征方式更为复杂，首先，以鼠妇遇到苹果来表示1，没有遇到表示0，4个苹果接触与否分别对应了4个一位的二进制数，在计算结束时，只有某一个特定的苹果被鼠妇接触，所以这4个二进制数只可能有一个数是1，从而表示其代表的十进制数是0、1、2、3中的某一个。这就是二进制独热码的一种应用，下页表中列出了解码过程中这两层不同的表征。

?

这个计算装置的使用者不需要知道鼠妇行走的细节，只要知道输入部分状态和输出部分状态的含义，就可以利用它进行计算了。对设计者来说，所做的事情不只是提取事物共同属性的抽象化，还需要为某种抽象过程能够被自动执行而进行构造。被构造出来的装置所做的事就是computing，对应“自动计算”，本文提到的“计算”都是指“自动计算”（为避免用词混淆，笔者认为创造相应的新词或许是有必要的，如可以将“自动计算”称为“器算”，或可以借用旧词“机算”）。

大卫·查默斯（D a v i d Chalmers）指出信息具有物理形式，他详细说明了结构化信息和符号信息对于二进制编码的数据表征事实的过程，举例说，“110111”中存储器（其物理形式是穿孔卡片上特定位置的孔）的某个特定的部分，才代表某人年龄是55岁。[3]在这里，存储器中数据的位置是一种结构化信息，阐述哪个位置对应年龄是一种符号信息，然后才能使二进制序列串表征55岁的事实。在本文的例子中，独热码是一种结构化信息，其具体的物理形式是鼠妇是否触碰苹果。而对于这种结构的解读，也就是独热码中1的位置怎样对应十进制数，则是一种符号信息。为了构造某种自动的计算装置，设计者需要关注结构化信息的物理形式以及对结构的解读方式。

到目前为止，这个鼠妇计算装置是不完备的，因为一个完整的计算实现（computing implementation）需要具备可级联性、扇出性、布尔完备性这样几个特征[4]，这里重点围绕可级联性开展讨论，如当前的这个装置在输出部分，采用鼠妇是否遇到苹果的方式来表示0，这样做存在一个缺陷——无法将计算结果为0和计算未完成这两种情况区分开来，于是就无法正确地将计算结果传递给下一个系统。另一个问题是，用以表征输入数据的事物状态变化形式（有无挡板）和用以表征输出数据的事物状态变化形式（鼠妇有无触碰苹果）不一致，这样就很难将此类计算装置相互连接起来去构造出一个更复杂的计算装置。

●改进的鼠妇计算装置

接下来，针对上面存在的问题，对装置进行改造。其中一个需要调整的地方，是对用以表征数据的材料也就是结构化信息的物理形式进行改造，使其具有一致的表征数据的状态变化形式。假设输入和输出部分都使用挡板来表示，那么在级联的过程中，就需要设计用鼠妇推动挡板的装置，显然，这很为难鼠妇，虽然说设置一个生物感应装置并借助机械设备来吊装积木挡板，也能够实现目的，但这样就太复杂了。相对而言，若将输入和输出都用鼠妇的行为来表征，则更为可行。例如，在图5的例子中，在实现与逻辑运算的过程中，无论是输入数据还是输出数据，都是由是否存在触碰苹果的鼠妇来表示的。

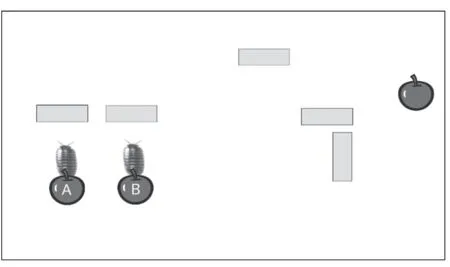
图5 一种用鼠妇行为表征输入和输出数据的与逻辑运算装置

这个与逻辑运算的具体实现过程还是很容易想象出来的，左下角A和B两个作为输入的苹果处，如果都没有鼠妇，则右侧输出必然没有鼠妇触碰苹果；如果只有一个鼠妇，则这个鼠妇会被困在墙角陷阱中，如果有两个输入，当其中一个鼠妇被困于墙角L形陷阱中后，另一个鼠妇触碰障碍（毕竟另一个鼠妇也是障碍）拐弯，最终到达作为输出的苹果位置。这恰好对应与逻辑运算的规则。当然，只有虚拟的理想状态下才能达到这样的效果，现实中的鼠妇在几次碰壁后是会从陷阱中逃脱的。以下各种方案都基于理想状态下的鼠妇行为，不再一一说明。

当输入和输出的事物状态变化形态统一后，就很容易采用各种简单的组件相互连接搭建出复杂的系统，如上页图6所示的装置的功能，是用两个输入数据进行与逻辑运算，再和第三个输入数据进行与逻辑运算。

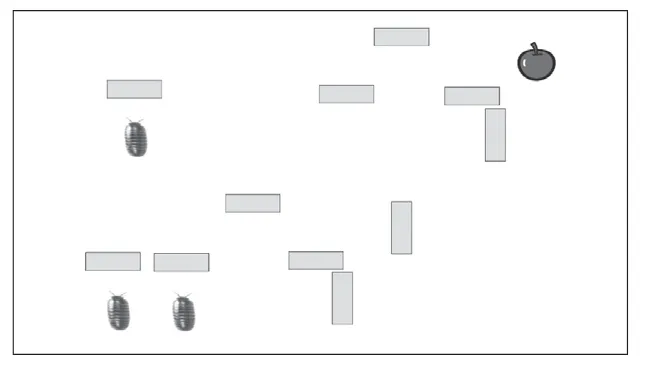
图6 级联的与逻辑运算的设计

要实现或运算，就稍微麻烦一些，需要引入一个叫做减速垫的装置（如图7）。当左下角A和B两个作为输入的苹果处都只有一个鼠妇时，当然只会有一个鼠妇到达输出的苹果位置；如果有两个输入，因为减速垫的作用，B处的鼠妇因触碰A处的鼠妇拐弯，从而无法到达输出的苹果位置，最终只会有一个鼠妇到达作为输出的苹果位置。

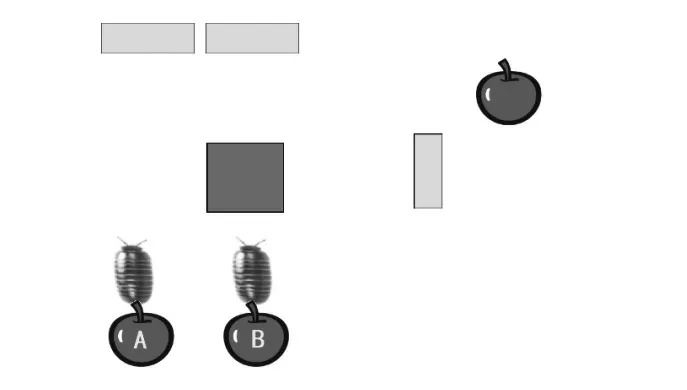
图7 或逻辑运算的设计

怎样用鼠妇来实现非逻辑的运算呢？可以引入一个鼠妇作为固定信号，如图8所示，当输入信号将这个固定信号拦截掉后，鼠妇就无法到达输出端，如果没有输入信号，这个固定信号就会到达输出端，于是对应了非逻辑运算。在图8的例子中，也同时解决了另一个重要的问题，就是要能区分结果为0和尚无结果这两种情况，解决的方法是再增加一个鼠妇作为计算是否已完成的时间信号，当这个时间信号鼠妇到达用圆圈表示的指定位置时，表示计算结果已经呈现。在这个时间信号的辅助下，可以确保鼠妇未能触碰苹果这一状态，确实表达了计算后0的结果。

图8 非逻辑运算的设计

借助时间信号和碰撞拦截，不仅可以实现非逻辑的运算，还可以实现其他逻辑运算，如果计算过程中，信号可以复制（假设鼠妇能在某种机构的作用下一分为二），那就能实现所有的逻辑运算功能。在一些生物计算机的设计中，就采用这种碰撞、拦截以及复制信号的方法来实现逻辑运算，限于篇幅这里不展开说明。自然界中许多事物天生具有可计算的特性，复杂的计算过程可以依赖非常简单的规则和行为构建出来，和本文所列举的仅存在于纸面上的理想实验不同，有研究者已用螃蟹群的碰撞来实现了逻辑运算。[5]甚至于不需要生物，依靠无生命的实物如台球，在理想的无摩擦的状态下碰撞，也能够构造出计算装置。[6]这种现象，被称为结构化信息的物理基底中立。

本文介绍的计算装置很容易借助图形化编程语言来实现，仅用鼠妇、挡板、苹果、减速垫这些简单的角色和行为规则，就能模拟出各种功能不同的计算过程，体现出用事物状态的变化来表征数据的思想方法，希望这种规则简单、构造和功能多样的虚拟计算装置能成为培养和考查计算思维的一种可供选择的平台。