基于近似动态规划的建筑能量管理系统日内优化调度方法
吴 雄,张子裕,刘炳文,麻 淞,曹滨睿,何雯雯,曹菁菁
(西安交通大学 电气工程学院,陕西 西安 710000)
0 引言
近几十年来,全球的能源消费模式发生了重大变革,建筑逐渐成为了主要的能源消耗终端,约占全球能源消耗总量的三分之一。随着城市化进程的继续推进,这一比例在未来仍会持续增高[1]。根据美国能源信息管理局的报告,建筑物内部主要的用电途径为供暖、通风和供冷,约占建筑使用总电量的51 %[2]。而由于建筑物如商业建筑等占地面积大,建筑物集成度高,人口密度大,这给城市电网和建筑能量管理带来了一系列的运营问题。一方面,为了维持建筑物内部的温度,需要暖通空调(heating ventilation air conditioning,HVAC)长时间通风、制热和制冷,消耗了大量的电力;另一方面,由于目前分布式电源如屋顶光伏逐渐集成到建筑物中,其带来的不确定性也逐渐成为目前建筑能量管理系统(buil-ding energy management system,BEMS)的难点。因此需要一种建筑能量管理方法来统筹考虑新能源不确定性和建筑内部特性。
目前,在建筑物内部进行温度控制的方式主要有空调和冷热电联产(combined cooling,heating and power,CCHP)。其中:文献[3]和文献[4]分别研究了HVAC 的二阶等效热负荷模型参数辨识方法和黑盒模型;文献[5]和文献[6]从消费者的角度出发,分别考虑了电动汽车需求和消费者舒适度以进行HVAC的协同调度;文献[7]提出了一种通过CCHP 实现智能建筑调度的建模方法,并采用集中母线的方式构建了智能建筑的能量管理调度模型;文献[8-9]基于CCHP 构建的建筑能量管理调度模型,分别考虑了碳交易和热储模型。然而上述研究大多仅考虑室内人员的温度或舒适度需求,并未结合实际统筹考虑通风辐照等因素带来的建筑内部温度变化,为此需进一步考虑室内外温度、辐照等影响建筑热惯性的因素,实现建筑内部的温度控制。
同时,由于可再生能源的高度随机性,楼宇中的分布式电源可能会对建筑系统的稳定性产生冲击。为了应对新能源的不确定性,文献[10]和文献[11]针对可能出现的最差场景,分别提出了一种商业建筑能量管理策略并使用鲁棒优化,从而应对新能源的随机性;文献[12]提出了一种基于机会约束的社区能源零售商能源管理与定价方法。然而上述研究多针对BEMS 的日前调度进行开展,根据系统预测的新能源出力曲线、负荷曲线等提前进行决策,难以应对可再生能源和负荷波动较大的情况,系统人员需要根据日内信息对BEMS 进行日内调度。在日内优化方面;文献[13]提出了一种基于规则的调整策略对居民住宅进行能量管理;文献[14]提出了一种模型预测控制(model predictive control,MPC)算法,通过随机规划实现日前调度,并由MPC 算法利用日内更新的随机量预测信息进行日内滚动调度。然而基于规则的调整策略易陷入局部最优解而忽略全局最优解,MPC 方法则过于依赖随机信息的预测精确度,易受到预测误差的影响。
近年来,近似动态规划(approximate dynamic programming,ADP)作为一种可以通过日内调度解决多阶段随机调度问题的算法,有望解决上述研究中的问题。ADP 由动态规划(dynamic programming,DP)演化而来并解决了DP 中的维度爆炸问题,其使用贝尔曼方程将多阶段随机优化问题转化为单阶段问题并迭代求解。ADP 通过历史数据进行主动学习,不依赖随机量的预测准确度和不确定集。文献[15]使用基于值函数迭代的ADP 算法对含新能源储能的微电网进行多目标调度;文献[16]基于ADP思想引入决策后状态近似值函数,以表征不同时段状态下的长期期望效益;文献[17]建立了基于分段线性函数的ADP 算法来解决大规模电网中的随机存储问题;文献[18]采用基于多维分段线性值函数近似的ADP 算法来解决多类型储能的调度问题。以上文献均验证了ADP 算法在多阶段随机优化方面的优越性。然而上述ADP 算法可在经济性上达到近似最优的结果,但涉及随机量波动小而影响较大的因素(如人体舒适度)时难以达到近似最优。
为此,本文提出了一种考虑建筑热惯性的MPCADP BEMS 日内调度方法,使用建筑热平衡方程描述建筑热惯性,使用ADP 算法应对日内调度的随机性问题并结合MPC 算法兼顾人体舒适度需求,该方法结合了MPC 和ADP 的优点,充分考虑了随机性,可兼顾建筑内部经济性最优和人体舒适度最优。
1 BEMS建模
1.1 BEMS
典型的BEMS 可由分布式电源(如风力发电机、光伏、建筑级CCHP 等电源)、储能装置、传感器、室温调控装置(HVAC)、其他电器负荷和能量管理平台组成。BEMS 一般与主网相连,其物理结构如附录A 图A1 所示。具体而言,CCHP 消耗天然气产生电能、热能和冷能,CCHP、光伏、风电和配电网购电共同组成建筑电源向建筑内部的不可调控负荷和HVAC 系统供电,由HVAC 和CCHP 产生的热能、冷能共同调控建筑内部的温度。
1.2 建筑围护结构热平衡
建筑围护结构热惯性模型是基于物理的模型,用于模拟建筑中室内空气、湿度和室外温度带来的室内温度变化。一般地,建筑物由内墙、外墙和门窗组成,太阳辐照平均散布在外墙与窗户上,考虑到外墙和窗户的材质差别导致的透光率不同,将二者分开计算。墙体节点温度主要受墙体热传导影响,墙体内表面温度不仅受墙体热传导影响,还受外墙辐照和窗户房间之间的热对流影响。假设房间墙壁两面收到光照,其中一面含窗,两面与相邻房间相连,将墙壁等效为热阻热容模型后如附录B图B1所示。
为了详细描述建筑物的热动态,建筑围护结构的墙壁热平衡[5]描述如下:
式中:n为区域标识;k为楼体标识;t为时段;C为墙体的热容;i,j分别为房间、墙壁标识;T为墙壁温度;T为屋内温度;T为相邻房间温度;R为墙壁的热阻为阳光照射到墙壁上的标识符,=1、=0 分别表示该墙壁受到、未受到阳光直射;A为墙壁面积;为墙壁的热通量吸收系数;Q为墙壁上的辐照热通量密度;Δt为间隔时间。
室内空气的节点温度受到多种因素的影响,包括外部因素(如温度和辐照)和内部因素(如建筑围护结构、内部热源),室内空气的热平衡方程如式(5)所示。其中:等号左侧为单位时间内热量变化值;等号右侧为单位时间内建筑内外壁和窗户向室内传递的热量、湿度传热、人体产热[19]、CCHP 和HVAC 产生热量。
式中:C为房间的热容;T为室外温度;R为窗户的热阻;为窗户的透光系数,A为窗户的面积,Q为照射在窗户上的辐照热通量密度,三者乘积即为窗户向室内传递的热量;m˙e为房间和室外之间的空气流量,cpa为水蒸气比热,两者与室内外温度差的乘积即为室内外湿度交换所引起的热量变化;Q为 室内 热 增益,如 人体产 出热 量;Q和Q分别为CCHP 供给的热量和冷量;EEER为能效比;PHVAC,t为HVAC的输出功率。
1.3 BEMS调度问题的建模
1.3.1 目标函数
本文以BEMS 的优化周期T(本文取T= 24 h)内的运行费用V最小为目标,如式(6)所示。
1)CCHP燃料费用。
CCHP 将输入的天然气转化为热能、电能和冷能,其输出的热能和冷能由燃气轮机的输出功率与效率决定,同时考虑热损失系数、制热系数、制冷系数和锅炉的回收效率,CCHP出力模型为:
式中:QMT,t为余热锅炉的输入热量,由考虑热损失后的燃气轮机的输出功率决定;PCCHPoutput,t和ηCCHPMT分别为CCHP 中燃气轮机的输出功率和效率;ηCCHP1为热损失系数;Qh0,t和Qc0,t分别为换热器输出的热量和吸收式制冷机输出的冷量,可用于室内温度热平衡模型中,由余热锅炉的输入热量、换热/冷系数和锅炉的回收效率决定;Kh0和Kc0分别为换热器的制热系数和吸收式制冷机的制冷系数,分别取为1.2 和0.95[20];ηCCHPrcc为锅炉的回收效率,由环境温度Tinn,k,t和环境系数T1、T2决定,其中T1、T2分别取值为573.15、423.15 K[20];VCCHPMT,t为设备中输入的天然气量,由燃气轮机的输出功率和天然气低热值L决定。
由此可得到CCHP的燃料费用为:
式中:wgas为天然气的购买单价。
2)机组运行维护费用。
机组运行维护费用包括CCHP 机组、风力发电机、光伏发电机组和储能的运行维护费用,具体为:
3)购电费用与售电收益。
式中:pmgp,t、pmgn,t分别为BEMS 向电网的购、售电电价;Pmgp,t和Pmgn,t分 别 为BEMS 向 电 网 的 购、售 电功率。
4)切负荷惩罚。
式中:Kloss为系统切负荷的单位惩罚费用;Ploss,t为切负荷功率。
5)人体舒适度惩罚。
本文BEMS 中人体舒适度采用预测平均评价(predicted mean vote,PMV)进行表征,该值综合考虑室内温度、空气流速、人体新陈代谢等有关因素,该值趋近于0 时为人体舒适度最佳[20],其中室内温度和墙壁温度由式(1)—(5)计算得到,故人体舒适度及人体舒适度惩罚定义如下:
式中:IPMV,t为人体舒适度;Tsk、D1、D2、M0、Icl、Ia和fcl分别为人体皮肤的正常温度、房屋与墙壁的面积系数、人体与外界的热量交换系数、衣物热阻、空气热阻和衣物面积,均为常数;为内墙温度;Lpmv为人体舒适度惩罚系数。
1.3.2 约束条件
BEMS 中人体舒适度采用PMV 进行表征,该值综合考虑室内温度、空气流速、人体新陈代谢等有关因素,取值范围为[-3,3][21]。PMV 与人体舒适度之间的关系详见附录C表C1。
本文根据ISO-7730标准将人体舒适区间设为:
同时,BEMS 还考虑了功率平衡约束、机组出力约束、储能装置容量约束和电网交换约束,相关约束的具体表达式详见附录C式(C1)—(C7)。
2 BEMS的MPC-ADP日内调度
2.1 ADP求解算法
BEMS 的日内调度为将一天分为NT个时段,在每个阶段均需做出当前时段至最终时段全局最优的决策。此类多阶段随机优化问题可表述为一个马尔可夫决策过程(Markov decision process,MDP),并用DP 方法求解。DP 可将多阶段问题分解为单阶段问题,并由转移函数实现前后时段的过渡。MDP 通常包含状态变量、决策变量和随机变量,前后2 个阶段的状态变量通过转移函数连接。
状态变量St是一组变量,可反映系统当前状态,在不考虑外来随机变量的干扰时,可直接由状态变量确定系统的决策。根据文献[22],对于含有“储能”的优化问题,将状态变量设为储能的荷电状态可以获得极好的效果,因此在本文BEMS 中,将状态变量St定义为:
式中:SSOC,t为储能的荷电状态。
决策变量xt反映系统在时段t所采取的决策,由系统中所有的可操作量组成,在本文BEMS 中定义为:
随机变量Wt表示时段t内所有的随机量,在本文BEMS中定义其预测结果W^t为:
转移函数表示St在注入xt和W^t后转移到下一时段系统状态变量St+Δt间的关系,本文中取Δt=1 h,故BEMS中的转移函数定义为:
式中:ηin、ηout分别为储能的充、放电效率。
考虑以上MDP元素,BEMS可重新定义为:
式中:Ct(t=1,2,…,NT)为t时段内的目标函数;EW^t[·]表示在考虑随机变量W^t时的期望。
由Bellman最优性原则,式(18)的尾部问题以时段t为分界可表示为(19)。
式中:Vt为时段t系统的价值函数,即从状态St开始的系统的最优成本,包括当前状态的成本和未来值函数;Vt+1为BEMS 从时段t+1 开始的运营成本到系统最后一个时段NT的成本;γ为MDP 问题中权衡系统即时奖励和未来奖励重要性的折扣因子,该值通常设置在0~1 之间;E[·]表示不考虑随机变量时的期望。
经典的DP 问题可通过反向求解贝尔曼最优方程得到单个时段每种可能的状态的值函数,再根据求得的值函数正向求解贝尔曼方程来得到最优解。然而在实际电力系统中问题的规模通常较大,过大的状态空间和动作空间会带来维度爆炸的问题,使得未来值函数的计算极其困难,即传统DP问题中的维度灾问题。因此,在ADP 中,通过分段函数对未来值函数进行近似,可给出近似最优解。
由于式(19)中的期望值计算量较大,文献[17]提出使用决策后状态变量代替状态变量来规避期望值的计算,决策后状态是指系统已进行决策但还未注入任何外来随机信息的状态。决策前状态、决策后状态、决策和随机变量之间的关系如图1所示。
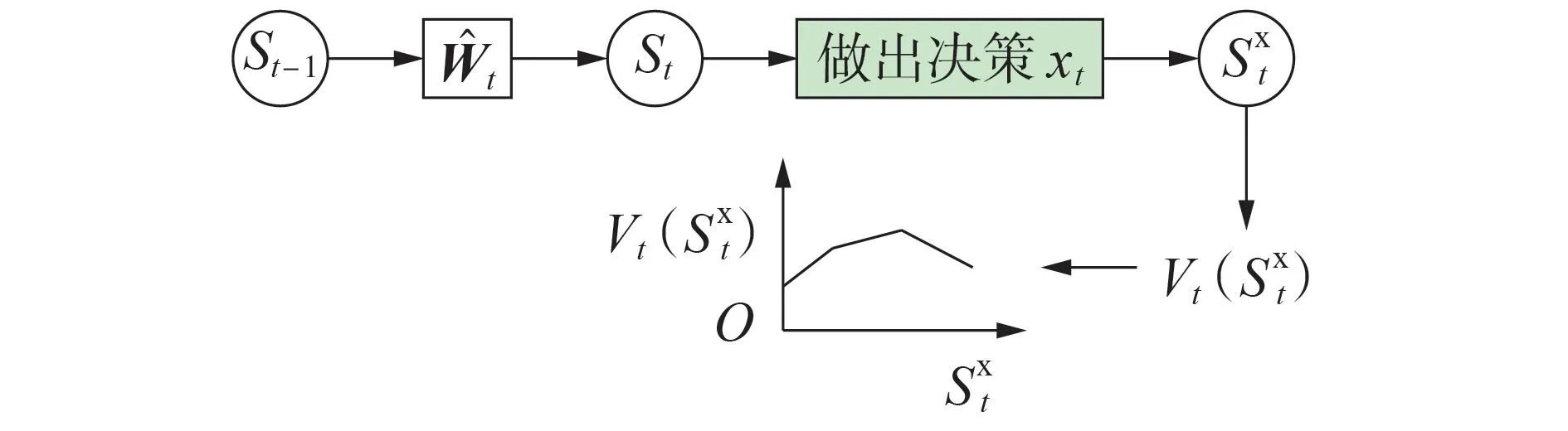
图1 ADP决策-状态转移过程Fig.1 ADP decision-state transition process
采用决策后状态变量代替状态变量后,系统的贝尔曼方程可表示为:
周教授一说,可蔓眼泪一下流了出来,说,真的穿越了哇?我好怕嘛。我要回去,我要回去找我妈嘛。说着就往外走。谷老板连忙拉住了,说,你瞎说个啥,你往哪儿走啊,你没看见外面啊?
式中:Nt为线性分段函数的分段数量为决策后状态变量即决策后的储能电池荷电状态,为横坐标,随着的增加,斜率递增;rt,a为段数索引a对应的横坐标长度。相关约束如式(22)、(23)所示。
式中:SSOC,max、SSOC,min分别为储能荷电状态上、下限。
则时段t的决策最优值可通过式(24)求解。
式中:Rt为所有rt,a的取值集合。
ADP算法通过前向求解每个时段的目标函数来得到每个时段的最优决策xt。为了更好地得到接近真实值函数的近似值函数,ADP 算法会对近似值函数进行多次迭代直至斜率收敛,即首先求得当次迭代中各时段的近似值函数结果和由近似值函数结果反推得到的决策后状态变量,为减少计算量仅更新决策后状态变量值所对应的分段处的斜率而非将整条分段线性函数所有分段的斜率全部更新,计算斜率时采用差分方法更新段数索引a处的斜率,为防止某次随机量波动过大带来的斜率骤变,将本次迭代与上一次迭代的斜率进行整合以得到本次迭代的临时斜率。最后为保持近似值函数的凹性,采用Leveling 方法对斜率进行修正以得到本次迭代的最终斜率并应用到下一次迭代中,具体说明如下。
在对分段线性函数斜率进行更新时,假设已完成s-1 次迭代,该次迭代的近似值函数已知,则将用于第s次迭代中贝尔曼方程的求解,如式(25)所示。
在第s次迭代的斜率更新中,首先按照式(26)计算第s次迭代中的状态变量采样观测值()。
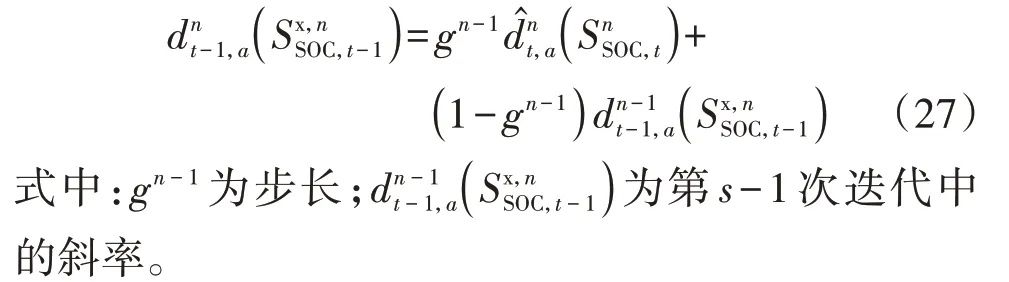
由此斜率更新中仅更新了第a段斜率的值,这可能会破坏分段线性函数的凸/凹性,针对此种情况需要对斜率进行修正。本文采用Leveling 方法[22]对斜率进行修正,如式(28)所示。
2.2 MPC-ADP日内调度方法
ADP 算法考虑了预测场景不准确的情况,由于训练场景为具有随机性的历史数据,在斜率收敛后的近似值函数可获得近似最优解。然而在日内调度中人体舒适度较为敏感,微小的温度变化会带来较大的舒适度变化,因此有必要在日内调度中依照日内反馈的信息在日前调度的基础上进行调整。
考虑目前预测信息的短期准确度较高,本文拟采用MPC 算法对短期内用户舒适度进行追踪,将人体舒适度加入日内调度的目标函数中,在时段t做出基于成本最优的决策后,在使决策变量偏离计算值最小的基础上,对人体舒适度进行追踪以达到人体舒适度最佳。
MPC 算法包括模型、滚动和反馈3 个部分。首先建立模型由当前时段的决策变量和状态变量得到下一时段的状态变量,即转移函数;然后结合未来p个时段的随机变量预测值进行优化,得到未来p个时段的决策变量,且只采用未来p个时段中第1个时段的决策,以此类推进行滚动优化;考虑到预测误差、参数误差、建模误差等因素,需要对已得到的决策进行反馈校正以弥补误差因素[23]。其中MPC 算法对控制对象的传统状态转移方程见附录D 式(D1)、(D2)。未来p个时段的状态转移函数和决策变量为:
式中:Yt为系统的预测输出矩阵;θt为系统扰动量的参数矩阵;φt为系统状态变量的状态矩阵;ΔXt为系统扰动量矩阵;Δxt为时段t+1 的状态变量相对于时段t状态变量的变化值;A、B为转移矩阵。
MPC算法通过滚动优化来保证在系统控制量扰动尽可能小的情况下将状态变量收敛到参考值,本文中为在系统决策变量扰动量尽可能小的情况下使人体舒适度尽快收敛到最优值。
式中:α和β分别为决策函数扰动量和人体舒适度函数的权重系数;Q和R为系数矩阵;Yl为状态变量参考值,本文设定为人体最优舒适度参考值0,即矩阵内部元素全为0;e为偏差;G和H为简化后的系数矩阵;P为常数。该式为MPC优化的目标函数,需使人体舒适度状态变量与人体最优舒适度参考值(本文为0)之间的差值最小,同时使MPC 优化中决策变量的与日内ADP 调度的偏离值最小,这由决策变量ΔXt和状态变量e决定。先在时段t求得未来p个时间段内使目标函数达到最优值的决策变量序列,只取序列中第1 个时段的决策变量执行,并求解此时状态变量和其与参考值的误差,迭代进入时段t+1后未来p个时段的MPC最优决策求解过程中。
同时,控制量和扰动量需满足如下约束:
式 中:xt,max和xt,min分 别 为 控 制 量 的 取 值 上、下 限;Δxt,max和Δxt,min分别为扰动量的取值上、下限。
综上所述,MPC-ADP 混合日内调度流程见附录D 图D1,具体步骤为:首先使用ADP 的离线训练从历史数据中训练得到未来值函数的分段线性函数并保存斜率,将已训练好的斜率代入日内调度中,以时段t为例,求得时段t的近似全局最优解xt和对应的状态变量St;然后由MPC 算法基于xt和St求解式(32),得到Δxt和Yt,本文中Yt即为用户最优的舒适度。收敛判据为训练过程中前后2 次迭代的斜率相差小于v。
3 算例分析
3.1 基本数据
本文以中国南部某小区的部分智能建筑作为计算场景,该区域有3 栋建筑物,每栋建筑物20 层,每层4 个房间,楼宇参数如附录E 表E1 所示。该区域现有CCHP、光伏发电机、风力发电机和储能,并可通过公共耦合节点与电网交换电量,机组参数如附录E 表E2 所示。BEMS 全天均参与能量管理,时间间隔为1 h。所有随机变量的历史数据的随机场景如附录E图E1所示。
在调度间隔内观察到的所有不确定的历史数据如图E1 所示,这些数据将用于ADP 方法的训练过程,以计算BEMS最终的运行成本。
对于ADP 问题,由于BEMS 能量管理问题是有界的,且未来时段内的成本与当前时段同样重要,因此将折扣因子设置为1。每个时段的分段线性函数分为10 段,初始斜率均为0。收敛阈值v=0.000 1。仿真通过Yalmip和MATLAB实现,并在具有3.70 GHz CPU 和16 GB RAM 的64 位PC 上运行,贝尔曼最优方程由CPLEX进行求解。
3.2 确定性模拟
本文提出的MPC-ADP 方法将确定性的BEMS日内调度问题作为基准,来分析其求解质量和计算性能,即使用单个确定性场景来迭代训练分段线性函数并由此进行日内调度,训练结果如图2所示。
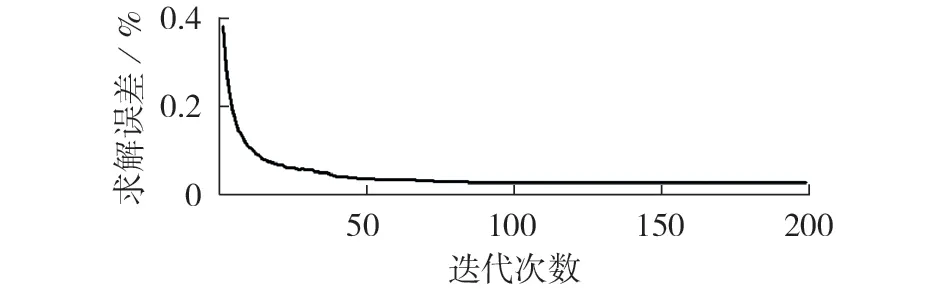
图2 确定性模拟MPC-ADP方法收敛曲线Fig.2 Convergence curve of deterministic simulation MPC-ADP method
由图2 可以看出:在确定性输入的情况下,本文所提MPC-ADP 方法在第100 次迭代时收敛,其收敛后相对于已知全天随机量信息的混合整数线性规划求解结果的求解误差为2.78 %。MPC-ADP 方法所求得的确定性算例日内调度方案、机组供热/冷方案分别见附录F图F1、F2。由图F1可看出:BEMS选择在电价较低时向电网买电并存储储能电量,在电价较高时选择售电或放电来降低成本,赚取利润;在一天内温度较高时,在CCHP 机组提供冷量的同时使用HVAC 对室内温度进行调节,此时空调负荷和不可控负荷叠加会产生新的峰值负荷,CCHP 大幅出力以满足电力需求;而在一天内温度较低时,由于此时购电电价也较低,BEMS 选择向电网购电来代替CCHP 机组系统供电以保证成本最低。而由图F2可看出:在夜间室外温度较低时由HVAC 供热,由于夜间电价比CCHP机组运行成本低,此时选用HVAC供热更为经济,而在白天室外温度较高时将由CCHP 和HVAC 同时制冷,由于日间电价比CCHP 机组运行成本高,此时优先使用CCHP 机组供冷,到达CCHP机组供冷上限后由HVAC供冷。
采用ADP 和MPC-ADP 方法时的人体舒适度对比如图3所示。由图可见:采用ADP 方法时,人体舒适度曲线整体呈现S 型,且全天内的舒适度仅有11:00为最佳,而其他时间内均处于人体舒适度范围的边界;采用本文所提MPC-ADP 方法后,人体舒适性大幅提升,几乎全天所有时间内均处于最舒适状态。
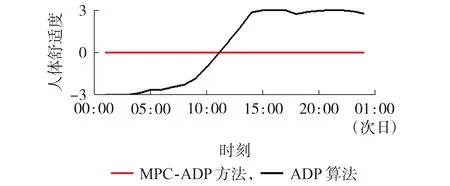
图3 采用ADP和MPC-ADP方法时的人体舒适度对比Fig.3 Comparison of human comfort between ADP and MPC-ADP methods
ADP、MPC-ADP 方法和混合整数线性规划模型的日内调度求解时间分别为0.80、0.83、2.35 s。这是因为ADP 算法和MPC-ADP 方法均将24 h 大规模混合整数线性规划问题分解为24 个单时段的小规模混合整数线性规划问题,而MPC-ADP方法比ADP算法多进行一次追踪求解。
3.3 随机性模拟
在随机性算例中,本文选取1 000个场景作为训练集,200 个场景作为测试集。同时将本文的MPCADP 方法与Myopic 短视策略和基于MPC 的前瞻H策略进行比较,结果如图4 所示。图中基于MPC 的前瞻H策略的H取为2 h。

图4 MPC-ADP与对比算法的收敛曲线Fig.4 Convergence curves of MPC-ADP and contrasting algorithms
由图4 可知:Myopic 短视策略和MPC 算法都只能获得具有较高误差的局部最优解,且其误差不会随着迭代次数的增加而呈现逐渐减少的趋势,而基于MPC-ADP 方法的求解误差会随着迭代次数的增加呈现逐渐收敛的趋势,并在700 次左右收敛至最优值,约为4.32 %,这证明MPC-ADP 方法会从历史数据中学习并逐渐收敛到全局最优解。
表1 进一步比较了200 个测试集中Myopic 短视策略、MPC 算法、ADP 算法和MPC-ADP 方法的求解误差Es和求解时间Ts,可以看出基于传统ADP 和MPC-ADP 方法的求解精度均较高,虽然MPC-ADP方法的求解速度稍慢于传统ADP 算法,但其能够大幅提高人体舒适度。

表1 测试集中4种算法的对比计算结果Table 1 Comparative calculation results of four algorithms in test set
4 结论
本文提出了一种MPC-ADP方法用于求解BEMS的多阶段随机日内调度问题,同时考虑了较为详细的建筑围护结构室温模型,结合MPC-ADP 方法实现人体舒适度最佳。本文使用大量历史数据离线训练MPC-ADP 方法的近似值函数,并将离线训练完成的值函数使用到日内调度中,结合MPC 算法在决策变量波动最小的基础上对人体舒适度进行优化。仿真结果表明,MPC-ADP 方法的求解误差相比于其他的日内调度算法更小,且相比于传统ADP 算法可大幅提高人体舒适度。
本文考虑的是值迭代的ADP 算法,在未来可进一步拓展为策略迭代的ADP 算法,同时针对非线性问题也可选取非线性的值函数进行近似。针对建筑内部的系统设计也可进一步细化,精细地考虑各项用能需求。
附录见本刊网络版(http://www.epae.cn)。

