城市配电网DG消纳能力曲线的计算方法与分析应用
肖 峻,王传奇,李晓辉
(1.天津大学 智能电网教育部重点实验室,天津 300072;2.国网天津市电力公司营销服务中心,天津 300202)
0 引言
分布式发电(distributed generation,DG)是新能源发电并网运行的一种有效形式[1]。随着DG 规模化接入配电网,传统无源配电网逐步演化为有源配电网[2]。有源配电网的安全运行面临新的问题,如线路过载、电压越限、潮流大小和方向改变等[3]。在此背景下,如何确定和提高配电网可以利用DG 出力的极限,成为一个备受关注的问题。
国内外学者普遍使用消纳能力(total accommodation capability,TAC)表征配电网的DG 承载能力。TAC 的定义为,在满足一定运行方式及安全约束的前提下,配电网可以利用的最大DG出力[4]。文献[5]提出TAC 不能超过25 % 的设备额定容量,该结果过于保守。文献[6]建立一系列宏观的渗透率指标,并利用DG最大匹配现状负荷的程度确定TAC,但是未考虑安全约束不适用于具体配电网。文献[7-8]建立DG 接入配电网的TAC 评估优化模型,利用分段计算方法或最优潮流对模型进行求解,但是单次求解的时间较长,不适用于负荷波动大的场景,并且只能得到TAC 对应的单一的DG 分布情况。文献[9]根据选择的负荷/DG场景,采用蒙特卡罗随机模拟法评估配电网的TAC,但结果受所选场景的影响较大,并且场景有限导致不能反映完整的TAC。针对上述问题,文献[10]在供电能力(total supply capability,TSC)曲线[11]的基础上,基于有源配电网的安全域和安全边界模型[12-13],提出TAC 曲线,TAC 曲线反映了有源配电网在任意负荷/DG 分布下的TAC,但“任意负荷/DG 分布”的假设条件仅适合从理论上分析TAC,计算得到的某些负荷分布下的TAC 过于理想,在实际系统中难以达到,对于实际城市配电网,还需考虑具体的边界条件。研究表明,负荷是影响TAC 的一个重要因素[14],实际馈线中的负荷接入位置和大小都不是任意的[15-16],因此,考虑馈线的实际负荷情况是TAC曲线实际应用的关键。
在确定配电网的TAC 后,还需进一步探究TAC的提升措施。文献[9]提出利用逆变器解决电压越限的问题进而提升TAC 的方法,但该方法的经济性差,控制复杂且TAC 提升有限。文献[17]引入高载能负荷的措施以及文献[18-19]允许功率倒送、跨区域多级协同的措施能够显著提升TAC,但只能反映具体场景下的TAC 提升效果,不能反映系统完整TAC 的提升效果。因此,有必要结合TAC 曲线的特点,分析负荷对TAC 曲线的影响,从而帮助规划人员合理配置负荷,以显著提升TAC。
本文提出一种城市配电网DG TAC 曲线的计算方法。首先,介绍安全域和安全边界;然后,在分析馈线负荷实际情况的基础上,提出本文的TAC 曲线模型及绘制方法;最后,采用改进的IEEE 33 节点系统算例进行验证,并与现有方法进行对比,基于所发现的负荷对TAC 曲线的影响规律,提出2 种TAC 曲线提升措施,能够明显提升系统完整TAC。
1 安全域与安全边界
由于TAC 曲线是通过安全域严格安全边界点绘制而成的,因此需要介绍有源配电网的安全域以及安全边界。
1.1 有源配电网的安全域模型
配电网安全域是状态空间中满足安全约束的所有工作点的集合[12]。文献[12]针对有源配电网,建立计及N-0和N-1的安全域模型。我国城市配电网普遍采用N-1安全准则。关于TAC曲线的研究目前仅考虑了正常运行约束,即N-0 安全约束,采用式(1)所示的N-0安全域模型[10]。
式中:ΩTQSR0为有源配电网N-0 安全域;W为工作点;WL为工作点的负荷节点部分;WDG为工作点的DG 节点部分;SLk为第k个负荷节点的流出功率;n为负荷节点数;SDGh为第h个DG 节点的注入功率,规定流出功率为正,本文负号仅表示方向;m为DG 节点数;r为网损系数,表示用固定比例计及网损,其值在计算安全边界点交流潮流后确定;cl为馈线段l的容量;c为馈线段容量构成的常向量;AL为负荷系数矩阵,ADG为DG 系数矩阵;alk为[AL,ADG]元素,表示第k个元素是否在第l组约束中,若在,则其取值为1,否则其取值为0。
式(1)中-c≤( 1+r)[AL,ADG]W为反向潮流约束,用于保证反向潮流不超过线路容量上限。本文允许10 kV 变压器和变电站主变(如110 kV 变压器)向上级电网倒送功率,同时允许DG 资源丰富的10 kV 馈线通过变电站10 kV母线向其他馈线传输功率[18]。
1.2 有源配电网的安全边界模型
安全域边界由状态空间边界和安全边界共同构成。根据是否满足严格临界性,安全边界又分为严格安全边界和非严格安全边界。无源配电网的严格临界性定义为任一负荷增长均会违反安全约束,严格安全边界定义为所有具有严格临界性的工作点集合[13]。与TSC 曲线[11]类似,描述配电网TAC 的TAC曲线应选用任一DG 出力都不能再增加/削减的严格边界。
文献[10]指出有源配电网具有4 种方向的严格临界性,其中与本文DG 消纳有关的2 种临界性是:DG 增长临界性,即任一DG 出力的增长引起反向潮流越限;DG削减临界性,即任一DG出力的减少引起正向潮流越限。
满足上述2 种严格临界性的工作点分别构成DG 上限边界Ω+β,DG和DG 下限边界Ω-β,DG。将式(1)的部分反向潮流约束取等,且覆盖所有DG 变量,得到一个DG 上限边界,如式(2)所示;将式(1)的部分正向潮流约束取等,且覆盖所有DG变量,得到一个DG下限边界,如式(3)所示。
式中:βDG+,j为第j个DG 上限边界;βDG-,j为第j个DG下限边界;ALe、ADGe、ce分别为取等约束的负荷系数矩阵、DG 系数矩阵和常向量;ALne、ADGne、cne分别为不取等约束的负荷系数矩阵、DG 系数矩阵和常向量;‖ -ADGe‖1表示计算矩阵中每列元素之和再取最大值,由于alk≥0,因此,利用‖ -ADGe‖1<0 表示ADGe中每列均存在不为0 的元素,即等式约束覆盖所有的DG变量。
2 城市配电网TAC曲线的建模与绘制
文献[10]通过采样DG 上限、下限边界以及将其按照DG 总出力从小到大排序,绘制得到TAC 上限曲线和TAC 下限曲线,适合从理论上分析TAC。为使TAC 曲线能够实际应用,还需要考虑城市馈线负荷的实际情况和电压约束。
2.1 馈线负荷的实际情况
我国城市配电网普遍采用N-1安全准则。在系统正常运行时,馈线需为与其有联络关系的馈线提供备用,因此其接入负荷量受到控制,这导致负载率不高,实际馈线负荷一般与馈线容量有明显差距,例如,单联络馈线满足N-1 的最大允许负载率不超过馈线容量的50 %[16]。我国浙江某市配电网各馈线实际日负荷曲线如图1 所示,图中馈线负荷是以馈线容量为基准的标幺值[20]。

图1 馈线日负荷曲线举例Fig.1 Example of feeder daily load curves
一般情况下,馈线单个负荷节点的最大负荷更是远小于馈线容量,而文献[10]计算TAC 曲线时假设节点负荷最大功率可达到馈线容量,这不符合实际情况。为此,本文采用更接近城市配电网实际负荷情况的日负荷曲线来计算TAC曲线。
本文发现TAC 下限曲线仅在理论上存在,当考虑负荷实际情况后,TAC 下限曲线退化为一条值为0的水平直线,可以认为该曲线不存在。实际城市配
电网的TAC 曲线仅有TAC 上限曲线,因此,可将TAC上限曲线简称为TAC曲线。
2.2 TAC曲线模型与绘制
在城市配电网中,负荷水平是影响TAC 的重要因素,同时,大规模DG 的接入增加了系统电压越限的风险。本文所提TAC 曲线模型考虑馈线负荷的实际情况和电压约束,具体模型如下。
在各节点日负荷曲线确定的状态空间中,采样得到具有DG 增长临界性且满足电压约束的边界点,计算边界点的DG 总出力,将其按从小到大的顺序排序并编号。以排序后的编号为横坐标以及DG总出力为纵坐标绘制曲线。TAC 曲线的数学模型CTAC如式(4)所示。
式中:i为TAC曲线上的点排序后的编号;VDGWi为边界点Wi上的DG 总出力,即在Wi的负荷/DG 分布下的TAC;WLi为Wi的负荷节点部分;WDGi为Wi的DG 节点部分;SL,min为各节点日负荷曲线谷值组成的向量;SL,max为各节点日负荷曲线峰值组成的向量;ΔUi为边界点Wi的节点电压偏移向量;ΔU+GB、ΔU-GB分别为电压上、下偏移国标值,对于10 kV 配电网,其值分别取为7 %、-7 %[21]。
针对某一具体的城市配电网,通过式(4)能够计算各种实际负荷分布下配电网消纳DG 出力的上限及对应的DG 分布,因此TAC 曲线描述了配电网的完整TAC。
本文借鉴文献[11]的TSC 曲线绘制方法来绘制TAC曲线,步骤如下。
1)确定状态空间。不同于文献[10]中TAC 曲线根据馈线容量确定状态空间,本文根据各负荷节点的日负荷曲线峰谷值确定对应的状态空间。
2)按一定步长在状态空间内等间隔采样,生成均匀分布的待判定工作点集合。采样步长可以根据计算规模和精度的要求灵活选取。
3)从工作点集合中筛选出满足式(2)的位于DG上限边界的工作点。
4)对DG 上限边界的工作点集合进行电压校验和修正。根据配电网辐射状的特点,采用文献[22]方法计算节点电压偏移,如附录A 所示。节点电压偏移ΔUi如式(5)所示,电压约束如式(6)所示。
式中:Au为电压偏移系数矩阵。若边界点满足约束式(6),则保留,否则删除。
5)计算保留工作点的DG 总出力,并按照大小对DG上限边界采样点进行排序和编号。
6)以排序后的编号为横坐标以及DG 总出力为纵坐标绘制TAC曲线。
3 算例验证与分析
在第2 章中,针对一般配电网建立了计及馈线负荷实际情况的TAC 曲线模型,这符合配电网规划建设的实际情况。本文的TAC 曲线绘制方法是对文献[10]方法的改进,文献[10,23]表明TAC 曲线的绘制方法具有普适性。下面结合具体算例对本文方法进行验证。
3.1 算例简介
IEEE 33节点系统算例如图2所示。

图2 IEEE 33节点系统算例Fig.2 Example of IEEE 33-bus system
为了模拟10 kV 城市配电网,将各线路的阻抗值缩小为原来的1/4,馈线容量为10 MV·A,将低压负荷均等效到10 kV[22],网损系数r=2 %。在节点6、17、32 接入DG,单个DG 节点的功率变化范围为[-10,0] MV·A。对负荷节点进行归并简化,形成3 个虚拟负荷节点L1、L3、L4,改进的系统结构如图3所示,图中B表示支路。

图3 改进的系统结构Fig.3 Improved system structure
3.2 TAC曲线的计算和绘制
算例的安全域为:
根据各负荷节点的日负荷曲线峰谷值确定状态空间。L1— L4的日负荷曲线如附录B 图B1 所示。由图可知,L1— L4的负荷变化范围分别为[0.39,1.00]、[0,0.05]、[0.03,1.40]、[0.17,0.98] MV·A。
步长取为0.2 MV·A,根据式(2)计算得到边界点234 560 个,根据式(5)、(6)计算得到满足电压约束的边界点22 173 个,这些边界点构成TAC 曲线,TAC 曲线情况如表1 所示。表中:Wi=[SL1,SL2,SL3,SL4,SDG1,SDG2,SDG3];ΔUmax为最大电压偏移;nmax为对应节点。采用相同的方法,根据式(3)得到TAC 下限曲线点。绘制TAC 曲线,如图4 所示,图中Wsample为某工作点。
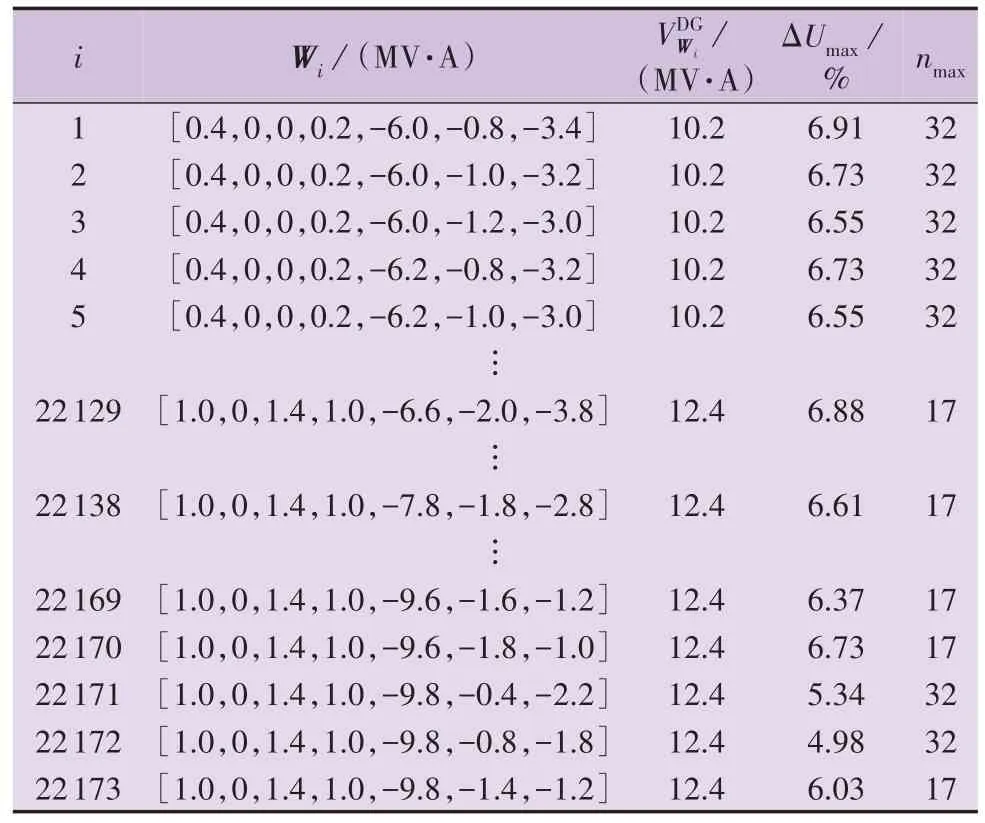
表1 TAC曲线情况Table 1 Condition of TAC curve

图4 系统的TAC曲线Fig.4 TAC curve of system
由图4可得如下结论。
1)TAC 曲线最低点为10.2 MV·A,TAC 曲线最高点为12.4 MV·A。根据表1计算平均值,得到平均TAC[10]为11.3 MV·A。曲线呈多个水平分段(图中为12段),这说明同一TAC 对应多个曲线点,即多个不同的负荷/DG分布状态。
2)TAC 下限曲线值恒为0。TAC 下限曲线的含义是,当有源配电网所带总负荷超出馈线段传输功率的上限时,为保证系统安全所需要的最小DG 出力[10]。根据2.1节可知,实际配电网的馈线总负荷均小于馈线容量,可由上级电网完全支撑,无需DG 出力来削减馈线正向潮流,因此,实际配电网的TAC下限曲线值恒为0,可以认为不存在。
3.3 与现有方法的比较
文献[7]方法是计算TAC 的一种典型方法,该方法以DG 总出力最大为目标函数,约束条件包括潮流约束、节点电压约束、线路容量约束、DG出力约束、与上级电网的联络功率约束以及有载调压变压器的调压范围约束。
在给定负荷分布条件下,利用文献[7]方法计算得到图4 中的工作点Wsample=[0.4,0,0.2,0.8,-6.6,-1.2,-3.2] MV·A,工作点Wsample处的TAC 位于TAC曲线上,这既验证了本文方法的正确性,也体现出本文方法比现有方法更具优势,能完整刻画配电网的TAC。
4 TAC 曲线的负荷影响因素与TAC 曲线提升措施
网络结构、馈线容量、馈线负荷、DG 接入位置、调压措施等均可能影响配电系统的TAC 曲线。本文在现有模型的基础上计及馈线实际负荷,分析负荷因素对TAC 曲线的影响,并提出提升TAC 曲线的措施。
4.1 负荷对TAC曲线的影响规律
4.1.1 瓶颈馈线段(组)
瓶颈馈线段(组)的定义为:若某馈线段(组)的反向潮流达到容量上限后,任一DG 出力均不能再增加,则该馈线段(组)为瓶颈馈线段(组)。瓶颈馈线段(组)具有以下特征:下游包含全部DG 节点以及最少负荷节点的馈线段(组)。对于任一配电网,可根据该特征确定瓶颈馈线段(组)。
在本文算例系统中,有1 个瓶颈馈线段(B2)和1 个瓶颈馈线组(B3,B7),如图5 所示。在图5(a)中,支路B2是瓶颈馈线段,其反向潮流达到容量上限后,任一DG 出力均不能再增加;在图5(b)中,B3和B7的反向潮流同时达到容量上限后,任一DG 出力也均不能再增加。
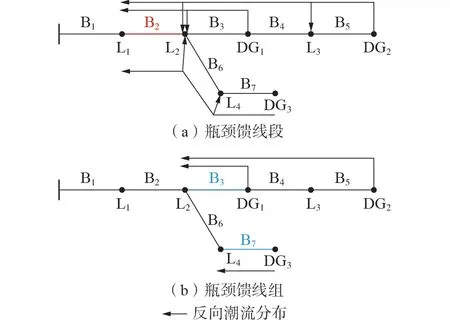
图5 计算TAC曲线时可能的潮流分布Fig.5 Possible power flow distribution in TAC curve calculation
4.1.2 影响规律
TAC 与瓶颈馈线段(组)上游负荷无关,仅与瓶颈馈线段(组)下游负荷呈正相关,这是由于上游负荷不会影响流过瓶颈馈线段(组)的反向潮流,而下游负荷会影响流过瓶颈馈线段(组)的反向潮流:当下游负荷增加时,流过瓶颈馈线段(组)的反向潮流将减小,为保证瓶颈馈线段(组)满载,需要增加DG出力;当下游负荷减小时,流过瓶颈馈线段(组)的反向潮流将增大,为保证瓶颈馈线段(组)不过载,需要减小DG 出力。因此,TAC 曲线仅与特定位置负荷,即瓶颈馈线段(组)下游负荷有关,负荷对TAC 曲线的影响规律如下。
1)瓶颈馈线段(组)上游负荷变化对TAC 曲线无影响。
2)瓶颈馈线段(组)下游负荷峰值减小时,TAC曲线高点下降;瓶颈馈线段(组)下游负荷谷值增大时,TAC曲线低点上升。
瓶颈馈线段(组)上游负荷L1和瓶颈馈线段(组)下游负荷L3、L4及其削峰填谷情况如附录B 图B2 所示,根据这些信息,在图B1(场景0)的基础上设计更多的场景来验证不同位置负荷对TAC 曲线的影响规律。各负荷场景设置如表2所示。

表2 负荷场景设置Table 2 Load scenario setting
场景0 — 3 下的TAC 曲线如图6 所示。由图可知:场景2 与场景0 下的TAC 曲线完全重合,场景3与场景1 下的TAC 曲线完全重合,这表明TAC 曲线与瓶颈馈线段(组)上游负荷无关;相较于场景0(场景2),在场景1(场景3)下,下游负荷峰值减小0.68 MV·A,TAC 曲线极大值由12.4 MV·A 减小至11.7 MV·A,下游负荷谷值增大0.7 MV·A,TAC 曲线极小值由10.2 MV·A增加至10.9 MV·A。

图6 场景0—3下的TAC曲线Fig.6 TAC curves under Scenario 0 to 3
4.2 TAC曲线的提升措施
负荷增加与馈线段(组)扩容能够提升配电网消纳DG 的能力,从而实现TAC 曲线的提升,但是本文研究发现,并不是任一位置的负荷增加和馈线段(组)扩容均能带来TAC 曲线的提升。基于负荷对TAC 曲线的影响规律,本文对上述2 种提升TAC 曲线的措施进行进一步的细化,具体如下。
1)措施1:增加瓶颈馈线段(组)下游负荷,这是由于TAC 曲线仅与瓶颈馈线段(组)下游负荷呈正相关。
2)措施2:瓶颈馈线段(组)扩容,这是由于瓶颈馈线段(组)是限制TAC曲线的一个主要因素。
在相同大小的新负荷接入下,措施1 可以实现TAC 曲线提升的最大化;措施2 针对的是具体的馈线段(组),可以减少额外线路扩容的投资。例如,对算例系统分别采取上述2种措施:在采取措施1后,新接入负荷用户使得L3功率增加2.0 MV·A;在采取措施2 后,将节点4 与节点5 之间的馈线段从10 MV·A扩容到11 MV·A。图7 展示了2 种TAC 曲线提升措施的效果。

图7 2种TAC曲线提升措施的效果Fig.7 Effect of two TAC curve improvement measures
由图7 可知:在采取措施后,TAC 曲线得到整体提升;在采取措施1 后,曲线极小值由10.2 MV·A 增加至12.2 MV·A,曲线极大值由12.4 MV·A 增加至14.4 MV·A,平均TAC 增加1.9 MV·A;在采取措施2后,曲线极小值由10.2 MV·A 增加至10.6 MV·A,曲线极大值由12.4 MV·A增加至13.4 MV·A,平均TAC增加0.6 MV·A。
从工程实际角度,上述2 种措施均能在配电网的发展中进行实施:措施1 可在供电业务扩展中新接入负荷时进行实施;措施2 可在改造工程中更换导线时进行实施。措施1 无须增加投资,更具优先性;措施2 需要额外投资,宜与配电网瓶颈馈线段(组)改造相结合,该措施适用于线路容量约束强于电压约束的配电网,即一般的城市配电网。
5 TAC曲线的应用
TAC曲线包含配电系统所有的安全边界点信息和每个边界点的负荷/DG在馈线上的分布数据,因此,利用TAC曲线可为系统规划提供帮助。
5.1 DG接入
TAC 曲线可以用于指导DG 接入。TAC 点的TAC 为DG 最大安装容量的确定提供了直接依据。考虑到DG 的可调节能力以及需求响应能力,实际中可以适当增加DG 的安装容量。此外,由于业主安装DG 的规模以及容量往往受到客观因素和主观因素的限制,配电网中不同位置的DG 可开发潜力是不同的。利用本文方法可以在DG 可开发潜力较小位置降低TAC,以换取DG 可开发潜力较大位置TAC 的提升。例如:表1 中编号为22 129 时,DG1—DG3的注入功率分别为-6.6、-2.0、-3.8 MV·A。DG1所在位置是可开发潜力最大的位置,其需求尚未被满足;表1 中编号为22 138 时,分别减小DG2、DG3的TAC 0.2、1.0 MV·A,可换取DG1的TAC增大1.2 MV·A,从而可满足DG1所在位置的需求。
5.2 负荷接入
相较于现有以TSC 为目标确定用户接入位置的方法[24],本文方法在指导用户接入位置选择时可以同时提高系统负载率和TAC。例如,根据4.2节的措施1,在下游负荷L3处新接入2 MV·A 的用户负荷来提高系统负载率,图7中采取措施1后的TAC曲线整体提升,平均TAC增加了1.9 MV·A。
5.3 导线更换
相较于传统配电网扩展规划方法得到的多条线路扩展规划[25]方案,本文方法聚焦于容量约束对TAC 的限制,确保所得导线更换方案能明显提升系统TAC。例如,根据4.2 节的措施2,将节点4 和节点5 之间的导线容量从10 MV·A 扩大到11 MV·A,图7中采取措施2后的TAC曲线整体提升,平均TAC增加了0.6 MV·A。
6 结论
对于有源配电网,DG TAC不应仅用1个数值来表示,而应用1条TAC 曲线来表示,该曲线描述了各种负荷/DG 分布下的TAC。本文提出考虑馈线实际负荷和电压约束的TAC 曲线模型及绘制方法。通过改进的IEEE 33 节点系统算例进行验证。与现有方法的对比表明,本文方法所得结果能更完整有效地描述实际城市配电网的TAC。主要结论如下。
1)当考虑实际负荷后,TAC 下限曲线一般不存在,仅存在TAC 上限曲线,这是由于实际馈线总负荷小于馈线容量。
2)馈线不同位置负荷对TAC 曲线的影响规律为:只有瓶颈馈线段(组)下游负荷会对TAC 曲线产生影响,基于此,提出增加瓶颈馈线段(组)下游负荷和瓶颈馈线段(组)扩容2种TAC曲线提升措施。
3)TAC 曲线在规划方面具有应用价值,可以指导DG接入、负荷接入和导线更换。
笔者后续将研究低压配电网、N-1 下城市配电网的TAC 曲线,进一步挖掘TAC 曲线在规划运行中的应用价值。
附录见本刊网络版(http://www.epae.cn)。

