光伏电站主变压器比率差动保护对单相接地短路故障的适应性分析

陈晓龙，朱雨葭，张 浩，王聪博，薛志英

（1.天津大学 智能电网教育部重点实验室，天津 300072；2.中国电力科学研究院有限公司，北京 100192）

0 引言

随着光伏装机容量逐年攀升［1-2］，光伏电站集中接入电网成为我国光伏并网发电的重要形式。光伏电站的容量通常高达几百兆瓦，其在输电网络中所占的发电比例不可忽略。另外，我国明确规定光伏并网逆变器需满足低电压穿越（low voltage ride through，LVRT）要求，即当电网发生故障时，光伏电站需保持并网，并根据故障严重程度输出一定的无功电流以支撑电网电压。

在光伏电站对输电系统继电保护的影响方面，现有文献大多聚焦于送出线路保护的研究，并且尚缺乏定量的故障分析计算。文献［3］分析了光伏电站的弱电源特性对送出线路继电保护的影响，并得出了光伏电站的弱电源特性会造成送出线路光伏电站侧的电流保护不能启动、纵联差动保护灵敏度下降以及距离保护拒动的结论，但该文献强调了所提弱电源特性主要体现在非接地故障中，并未对接地故障下光伏电站接入对继电保护的影响进行分析。文献［4］推导了不同故障穿越控制目标下的逆变型电源输出电流表达式，并利用基尔霍夫电流定律，定性分析了送出线路发生两相短路故障时故障点两侧各相电流之间的相位关系，从而得出逆变型新能源场站的输出电流特性使得送出线路电流纵联差动保护灵敏度降低的结论，但由于缺乏定量分析，该文献所得结论难以为送出线路的电流纵联差动保护改进提供具体的参考依据。且文献［3］和文献［4］均未考虑LVRT 要求对逆变型新能源场站故障输出特性的影响。文献［5］研究了三相短路故障下具备LVRT能力的光伏电站对送出线路比率制动式和标积制动式电流纵联差动保护的影响，但该文献对故障点两侧电流的相位变化分析仍然仅基于定性讨论，缺乏详细可靠的定量分析计算支撑其理论分析结果，而保护适应性分析需建立在准确的故障特性分析基础上。

主变压器的差动保护包含比率差动元件、二次谐波制动元件和差动速断元件。在光伏电站接入对主变压器差动保护的影响方面，谐波制动元件的影响已有较为成熟的研究成果［6-7］。但是，比率差动元件作为主变压器差动保护的主要动作元件，光伏电站接入对其动作的影响尚未得到详细分析。文献［8］认为当光伏电站不具备LVRT 能力要求时，由于其在故障期间无须对故障点提供无功支撑，因此流经故障点两侧电流的相位差为180°；而当光伏电站具备LVRT 能力时，故障点两侧电流的相位差小于180°，从而使得主变压器差动保护灵敏度降低。但该文献并未给出详细推导过程作为理论依据，也未计及主变压器绕组接线方式的影响，相应结论待进一步验证。

鉴于单相接地短路故障为工程实际中最常见的短路故障，本文面向具备LVRT 能力的光伏电站，分析了主变压器两侧出口处发生单相接地短路故障时短路点故障电流幅值和相位的变化规律。在此基础上，结合主变压器差动保护的比率制动原理，在计及主变压器绕组接线方式的前提下，通过计算差动电流与制动电流的比值，分析了光伏电站对主变压器比率差动保护的影响。最后，基于MATLAB／Simulink的仿真结果验证了理论分析的正确性。

1 光伏电站控制策略及输出特性

1.1 光伏电站并网结构

光伏电站经主变压器升压后接入电网的示意图见图1。图中：光伏电站中的光伏发电单元1 —n各自通过箱式变压器T1，1— T1，n升压并联至公共连接点（point of common coupling，PCC）；PCC再与升压主变压器T2相连，T2的高压侧经送出线路接入110 kV输电网（T2采用YNd11的接线方式，其低压侧由接地变压器T3提供中性点接地，高压侧采用中性点直接接地［9］）；Es为交流系统等值电势；I1、I2为主变压器两侧电流，以流入主变压器为正方向。

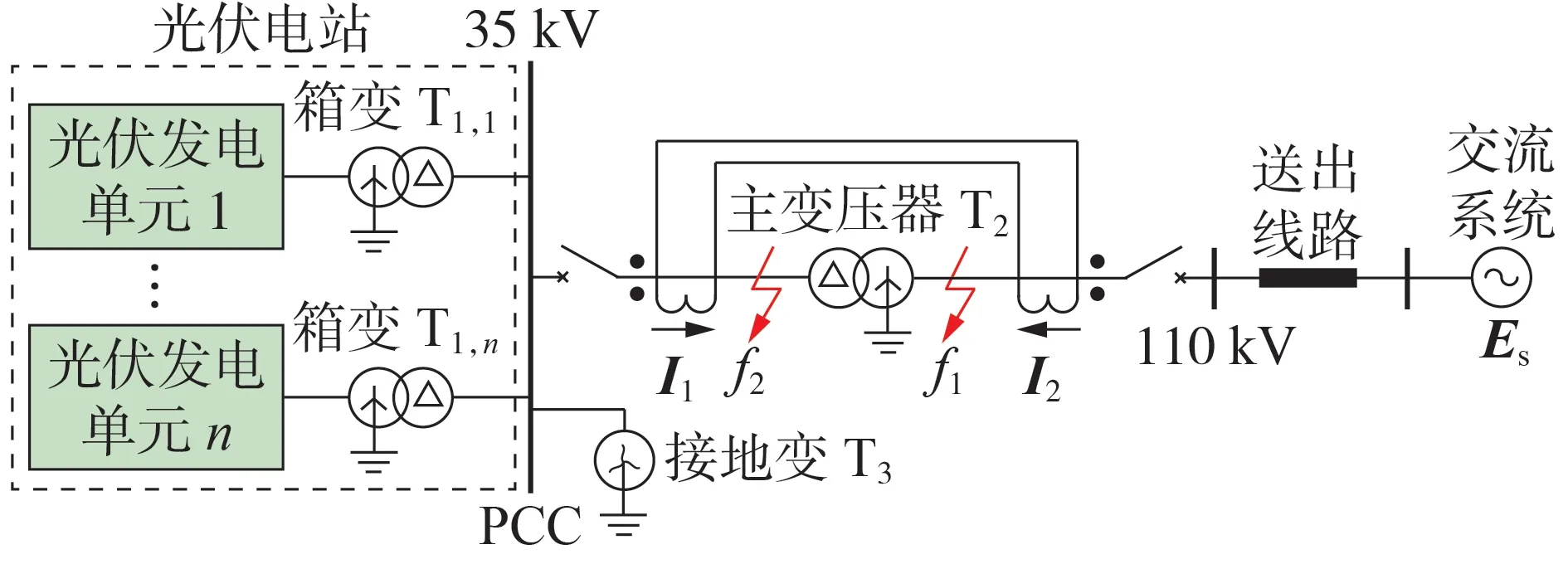
图1 光伏电站并网示意图Fig.1 Schematic diagram of grid-connected photovoltaic power generation system

1.2 光伏发电单元控制策略及输出特性

本文采用电网电压定向矢量控制实现逆变器输出有功功率与无功功率的解耦控制。

根据GB／T 37408—2019《光伏发电并网逆变器技术要求》，光伏并网逆变器需具备LVRT 能力，即电网发生故障时，并网逆变器需根据其出口处并网点电压跌落程度向电网提供一定的无功支撑［10］。光伏电站的输出特性由逆变器控制策略决定［11］。

本文采用正序分量控制策略［12］，故障期间采用逆变器出口处电压的正序分量为参考值，其输出电流Ig三相对称，且与并网点正序电压相位满足式（1）。

根据最新标准要求，在不对称故障期间，光伏并网逆变器输出动态无功电流的最大有效值不宜超过40 % 的额定电流。基于此，单相接地短路故障穿越时逆变器输出的无功电流和有功电流参考值的设置分别见附录A 式（A1）和式（A2）。根据式（A1）和式（A2）可得发生单相接地短路故障时，光伏电站输出电流滞后并网点正序电压的相位范围为［0°，22.4°］。当为逆变器并网点正序电压幅值；UN为并网点额定电压值）时，光伏电站仅输出有功电流，其输出电流与并网点正序电压保持同相位；当/UN≤0.9 时，光伏电站同时输出有功和无功电流，输出电流滞后并网点正序电压一定角度。

2 主变压器单相接地短路故障特性分析

基于正序分量控制策略，在进行故障分析计算时可将其等效为受并网点正序电压控制的电流源模型［13-16］。

2.1 主变压器高压侧单相接地短路故障特性分析

设图1 中T2高压侧出口f1处发生单相（A 相）接地短路故障。根据对称分量法，可得故障复合序网图如图2所示。图中：下标1表示单相接地短路故障发生在主变压器高压侧，下标（1）、（2）及（0）分别表示正序、负序及零序分量，后同；Es1为110 kV交流系统等值电势；Zs为系统等值阻抗；Is1为系统电源侧提供的故障电流；Ig1为光伏侧输出电流，U+g1(1)为逆变器出口处并网点正序电压，两者满足式（1）所示关系；If1为故障点接地电流；Uf1为故障点电压；ZT1为箱式变压器等效阻抗；ZT2为主变压器T2等效阻抗；ZL为送出线路等效阻抗；Rf1为短路点过渡电阻。

图2 主变压器高压侧单相接地短路故障复合序网图Fig.2 Composite sequence diagram of single-phase grounding short circuit fault on high-voltage side of transformer

通常情况下，线路的正序阻抗和负序阻抗相等，其零序阻抗为正、负序阻抗的3 倍，因此ZL（0）=3ZL（1），ZT2（1）=ZT2（0），Zs=Zs（1）=Zs（2）=Zs（0）。令ZLS（1）=ZL（1）+Zs（1）、ZLS（2）=ZL（2）+Zs（2）、ZLS（0）=3ZL（1）+Zs（0），则负序综合阻抗满足Z∑（2）=ZLS（2），零序综合阻抗满足Z∑（0）=ZLS（0）//ZT2（0）。

根据单相接地短路故障的边界条件，可求得短路点故障电流的表达式为：

另外，结合图2 所示的故障序网图，可得系统电源侧提供的故障电流各序分量表达式为：

可得系统电源侧提供的故障电流表达式为：

由式（2）、（4）可知，短路点故障电流与系统电源侧提供的故障电流均受过渡电阻及光伏侧输出电流的影响。

由1.2节已知，光伏侧输出电流的相位与并网点正序电压的相位及幅值有关。因此，为了得出光伏侧输出电流相位的变化规律，需分析并网点正序电压相位的变化规律。根据正序故障等值网络可得：

式中：ZT=ZT1(1)+ZT2(1)=jXT，XT为ZT1(1)和ZT2(1)的电抗。

令并网点正序电压U=U∠φu1，光伏侧输出电流Ig1=Ig1∠φi1，系统等值电势Es1=Es1∠0°。通过将式（5）中各项拆分为实虚部的形式，可以推导出故障期间并网点正序电压相位φu1的表达式为：

式中：各变量的表达式详见附录A式（A3）。

由式（6）、（A3）可见，并网点正序电压的相位φu1主要与Rf1、U、Ig1及φiu1有关。其中，U主要由Rf1决定，且根据式（A1）可知φiu1由U+g1(1)决定，而Ig1与光伏电站并网容量有关。因此，可得出影响并网点正序电压相位的主要因素为Rf1及光伏电站并网容量。进一步地，结合式（6）和式（A3）可分析得出：当光伏电站并网容量一定时，过渡电阻越大，φu1越小；当过渡电阻一定时，光伏电站并网容量越大，φu1越大。

参考某110 kV 光伏电站的实际参数，其主变压器短路电压百分比为10.5%，接地变压器零序等值阻抗ZT3（0）=0.306+j9.188 Ω，送出线路长度为15 km，送出线路正序阻抗ZL（1）=1.95+j5.82 Ω，且线路零序阻抗为正序阻抗的3 倍。交流系统等值阻抗Zs=0.893+j5.21 Ω。鉴于单相接地短路故障时短路点电压跌落程度较轻，考虑并网点正序电压跌落最严重的情况，即发生金属性单相接地短路故障时，经计算可得并网点正序电压幅值约为0.7UN。因此，结合不对称故障期间的LVRT 要求，根据式（6）可以估算出当并网容量小于600 MV·A 时的光伏侧输出电流的相位变化范围。为便于计算，本文假设变压器容量与并网容量一致。取Rf1=5 Ω，对应的并网点正序电压幅值满足0.7＜/UN≤0.9，可以得出此时光伏侧输出电流的相位变化范围为（-15°，60°）。同理，取Rf1=20 Ω，对应并网点正序电压幅值满足0.9＜/UN＜1 的情况，进一步计算得到光伏侧输出电流的相位变化范围为（0°，35°），此时光伏侧仅输出有功电流。进而将Ig1代入式（2）可得出短路点故障电流随光伏电站并网容量和输出电流相位变化的规律，如附录A图A1所示。

2.2 主变压器低压侧单相接地短路故障特性分析

主变压器T2低压侧出口f2处发生A相接地短路故障时的故障复合序网图如图3所示。图中：下标2表示单相接地短路故障发生在主变压器低压侧，后同；具体变量定义可参考高压侧，此处不再赘述。

图3 主变压器低压侧单相接地短路故障复合序网图Fig.3 Composite sequence diagram of single-phase grounding short circuit fault at low-voltage side of transformer

令ZLST(1)=ZL(1)+Zs(1)+ZT2(1)，则故障等值电路的负序综合阻抗满足Z′∑(2)=ZLST(2)=ZL(2)+Zs(2)+ZT2(2)，零序综合阻抗满足Z′∑(0)=ZT3(0)。

同理，可求得短路点故障电流表达式为：

式中：各变量的表达式见附录A式（A4）。

由式（10）可以看出，当主变压器低压侧出口处发生单相接地短路故障时，并网点正序电压相位的变化规律与高压侧一致。

同样地，考虑并网点正序电压跌落最严重的情况，计算得出主变压器低压侧发生金属性单相接地短路故障时并网点正序电压幅值约为0.8UN。以过渡电阻Rf2分别取为1、10 Ω的情况为例，其分别对应0.8＜/UN≤0.9 和0.9＜/UN＜1 的情况，并进一步计算得到光伏侧输出电流相位的变化范围分别为（-22.5°，45°）、（0°，30°），此处不再赘述。进一步地，将Ig2代入式（7）得出短路点故障电流随光伏电站并网容量和输出电流相位变化的规律见附录A图A2。

3 主变压器比率差动保护适应性分析

3.1 主变压器比率差动保护原理

主变压器广泛采用具有比率制动特性的差动保护原理，其中，常见的两折线比率制动原理的动作判据如式（11）所示。

式中：k为比率制动系数，通常取0.5～0.8［15］，考虑对比率差动保护最不利的情况，本文将其取为0.8；Iop为差动电流；Ires为制动电流；Iset.min为最小动作电流整定值；Ires.min为最小制动电流整定值。

拍摄高山土拨鼠并非一件困难的事。在偏远山区徒步旅行时，我遇到了这种腼腆的生物。同时我也发现，相对来说栖息在澳大利亚Grossglockner的土拨鼠更适应人类的接近。如果你有足够的耐心，并且行动缓慢，就有可能拍下类似这张照片的超广角画面。不过，不要指望在第一次拍照时它们的眼睛就能够对焦准确！在这张照片中，土拨鼠从背景略脏的风景中探出头，像大头钉一样尖锐，选择光圈f/8会增强视觉效果。在阴天拍摄，效果也会非常不错。在后期处理时，高对比度的天空没有什么优势，除非你是在清晨或者傍晚拍下的。为了处理最后的图像，我在Camera Raw软件中降低了高光，增加了阴影。

根据文献［17］和文献［18］中过原点的整定方法对式（11）中各参数进行整定。进一步地，设差动电流与制动电流之比m=Iop/Ires。比率制动特性曲线如附录A 图A3所示。图中：黑色实线为比率制动特性曲线；当主变压器保护动作区内发生故障但m＜0.8时，比率差动保护拒动，如红色虚线所示。

基于上述整定方法，结合文献［5］中对比率差动保护的灵敏系数Ksen的定义，可以得出式（12）所示关系。由式（12）可知，比率差动保护灵敏度与m成正比，从而可通过差动电流与制动电流之比m反映比率差动保护灵敏度的变化。

3.2 YNd11 接线方式下主变压器比率差动保护计算方法

设IYA为主变压器星形侧A 相电流，I△a为主变压器三角形侧A 相电流，两侧A 相线电流的正、负序分量关系如式（13）所示。同理可得B、C相同理线电流的正、负序分量关系，本文不再赘述。

式中：nT为主变压器变比。

上述两侧电流之间的相位差会使得主变压器正常运行或发生区外故障时计算得到的差动电流不为0，因此分析YNd11 接线方式下主变压器比率差动保护的动作性能时，需根据附录A 式（A5）、（A6）对差动电流与制动电流进行计算，从而减小不平衡电流的影响，并保证在主变压器正常运行或区外故障时差动保护不会误动［17］。

3.3 主变压器比率差动保护适应性分析

当主变压器高压侧出口处发生A 相接地短路故障时，2.1节中的短路计算为故障等效计算。在进行差动保护计算时，根据式（A5）、（A6）可得：

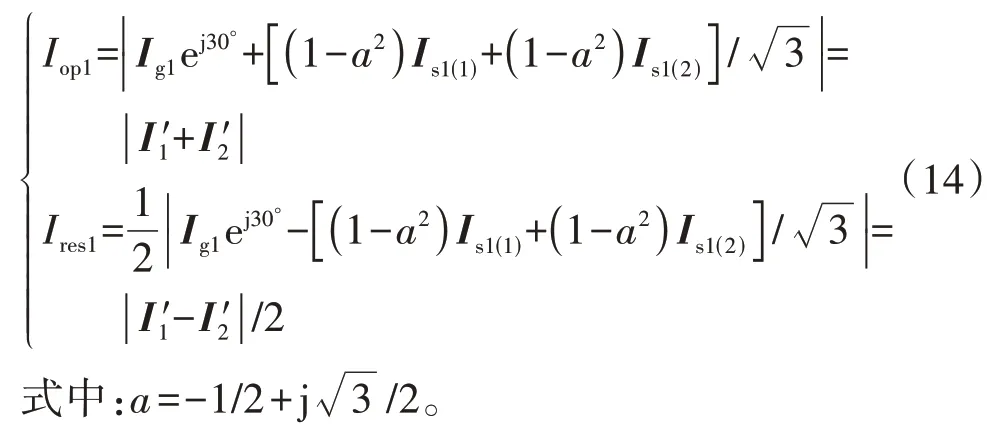
设I′1与I′2之间的夹角为θ，由平行四边形法则可知，式（14）可表示为：

根据2.1 节计算所得Is1各序分量与If1各序分量及Ig1的关系，结合式（15）可得不同工况下I′1和I′2的相量图，如图4所示。图中：α1为Ig1、If1间的夹角。

图4 主变压器高压侧出口处发生单相接地短路故障时的电流相量图Fig.4 Current phasor diagram when single-line-to-ground fault happen on high-voltage side

同理，当主变压器低压侧出口处发生A 相接地短路故障时，根据式（A5）、（A6），并结合对称分量法计算得到的A相差动电流与制动电流如下：

同样根据平行四边形法则对差动电流与制动电流进行化简计算以分析各电流量之间的关系。将2.2 节所得系统电源侧提供的各序故障电流与短路点故障电流正序分量及光伏侧输出电流的关系代入式（16），可以得到式（17）所示的表达式。

式中：β1为Ig2与If2(1)之间的夹角，由于短路点故障电流满足If2=3If2(1)，因此β1即为短路点故障电流与光伏侧输出电流的夹角。

由式（17）可得，此时差动电流与制动电流的相对大小主要取决于If2与Ig2的相对大小及β1。Ig2大小一定时，若β1＞90°，则β1越大，制动电流越大。β1一定时，若满足β1＞90°或β1＜90°且2|Ig2|＞|If2(1)|cosβ1，则Ig2幅值越大，制动电流越大。因此，β1增大或Ig2幅值增大均可能使得制动电流增加，从而使得主变压器比率差动保护灵敏度下降，并存在拒动风险。

此外，为了更加准确地分析比率差动保护的动作情况，首先以主变压器高压侧出口处发生单相接地短路故障为例，计算故障相和非故障相的差动电流与制动电流之比，如式（18）所示。

式 中：Z1=ZT2(0)+ZLS(0)；Z2=3Rf1+Z1+ZT2(0)ZLS(0)；Z3=Z2+2ZLS(1)Z1；m1_A、m1_B和m1_C分别为主变压器高压侧出口处发生A 相接地短路故障时，A、B、C 相的差动电流与制动电流之比。

由式（18）可知，将星形侧电流折算至三角形侧时，由于C 相差动电流计算公式中含有故障相A 相电流，因此对应的m1_C并不为0。考虑到比率差动保护采用三相“或门”逻辑，当任意相差动电流满足动作条件时，比率差动保护便会动作。因此，还需分析C相差动保护的动作情况。

主变压器低压侧出口处发生单相接地短路故障时各相差动电流与制动电流之比如式（19）所示。

式中：m2_A、m2_B和m2_C分别为主变压器低压侧出口处发生A 相接地短路故障时，A、B、C 相差动电流与制动电流之比。

3.4 光伏电站并网容量对比率差动保护的影响

根据式（18）所得计算结果，结合前文理论分析，可得在不同过渡电阻取值下，m1_A和m1_C随光伏电站并网容量及输出电流相位变化的规律见附录A 图A4。由图可见，当光伏电站并网容量大于200 MV·A时，Rf1=20 Ω 情况下的m1_A和m1_C恒小于Rf1=5 Ω 情况下的对应数值。这意味着当过渡电阻较大时，比率差动保护的灵敏度更低。此外，当Rf1=5 Ω 时，根据m1_A和m1_C的变化规律可以看出，比率差动保护存在故障相保护灵敏度降低的问题，但保护拒动的风险较小。而当Rf1=20 Ω 时，m1_A、m1_C的值均存在小于0.8 的情况，即当过渡电阻较大时，主变压器比率差动保护存在拒动的风险。

由式（19）可知，当主变压器低压侧出口处发生A相接地短路故障时，非故障相B相和C相的差动电流均为0，此时比率差动保护的动作情况由A 相决定。在不同过渡电阻下，故障相A 相差动电流与制动电流之比的变化规律如图5所示。

图5 低压侧故障下差动电流与制动电流的比值变化规律Fig.5 Law of change in ratio of differential current to braking current under low-voltage-side fault

由图5 可知，此时A 相差动电流与制动电流之比的变化规律与高压侧类似，即该比值均随着光伏电站并网容量的增加和输出电流相位的增加而减小。但是，与高压侧单相接地短路故障相比，低压侧故障下m2_A的最小值更小，且在较大范围内m2_A均小于1。因此，主变压器低压侧出口处发生单相接地短路故障时比率差动保护拒动的可能性更大。

3.5 交流系统强度对比率差动保护的影响

考虑到实际工程中主变压器的容量有限，本节引入短路容量比RSCR表征交流系统与光伏电站的相对强弱［6］，其表达式如式（20）所示。

式中：Un为110 kV 侧额定电压；SPV为光伏电站并网容量。当RSCR＜3时，交流系统为弱电网。

以光伏电站并网容量为230 MV·A 为例（对应主变压器容量取为240 MV·A），通过改变交流系统等值阻抗分析交流系统强度对比率差动保护的影响。同样遵循前述分析思路，以低压侧为例，可以估算出当0.7≤U/UN≤1 且2＜RSCR＜10 时，光伏侧输出电流的相位变化范围为（-30°，60°）。进一步地，代入Rf2及Ig2即可得出m2_A的变化规律，如附录A 图A5所示。由图可以看出，当RSCR较小时，m2_A的值可能小于0.8，比率差动保护存在拒动的可能。

综上所述，当光伏电站接入的主变压器两侧出口处发生A 相接地短路故障时，主变压器比率差动保护的动作结果主要受光伏侧和交流系统相对强弱的影响；在单相接地短路故障下，比率差动保护抗过渡电阻的能力较弱；另外，改变交流系统等值阻抗与改变光伏电站并网容量有类似的影响规律。

4 仿真验证

本文基于MATLAB／Simulink 仿真平台搭建如图1 所示的光伏电站并网模型，以验证上述短路点故障电流变化规律与比率差动保护适应性分析的可靠性。仿真系统采用的各阻抗参数与前述分析计算中所用各参数一致。

4.1 主变压器两侧出口处发生单相接地短路故障时故障点接地电流的变化规律

4.1.1 主变压器高压侧出口处发生单相接地短路故障时的短路点故障电流变化规律

以主变压器高压侧出口处发生单相接地短路故障为例，通过改变光伏电站并网容量，分别验证当Rf1取5 Ω 和20 Ω 时短路点故障电流的变化规律，结果如附录B 表B1 所示。由表可以看出，随着光伏电站并网容量的增大，Ig1与If1的夹角变化较小，If1的幅值随光伏电站并网容量的增大而略有增加。由3.2 节的分析可知，当夹角α一定时，影响主变压器比率的主要因素为Ig1与Is1的相对大小。

4.1.2 主变压器低压侧出口处发生单相接地短路故障时的短路点故障电流变化规律

当主变压器低压侧出口处发生单相接地短路故障时，If2的变化规律见附录B表B2。由表可以看出，主变压器低压侧故障下，由于故障序网的等值阻抗较高压侧更大，故Ig2大小的改变对If2幅值的影响更小。通过对比表B1、B2 可以发现，光伏侧同时输出有功和无功电流时，其输出电流与短路点故障电流的夹角均大于光伏侧仅输出有功电流的情况。除此之外，短路点故障电流变化规律与主变压器高压侧出口处发生单相接地短路故障时类似。表B1 和表B2所得仿真验证结果均与前述理论分析结果一致。

4.2 主变压器比率差动保护动作性能分析

4.2.1 情形1：主变压器高压侧出口处发生单相接地短路故障

以Rf1取5 Ω 和20 Ω 为例，主变压器高压侧出口处发生单相接地短路故障时，m1_A、m1_C受并网容量影响的变化规律分别如附录A图A6、A7所示。

由图A6（a）可知，当Rf1较小时，由于Ig1与Is1的幅值差较大，光伏电站并网容量的增加对故障相比率差动保护的影响主要为使其灵敏度逐渐降低，但是不存在拒动的问题。另外，由图A6（b）可见，m1_C的变化规律与m1_A不同：m1_C不随着光伏电站并网容量的增加而单调变化。由于当Rf1较小时，m1_C的值远大于0.8，结合A、C 两相比率差动保护的动作情况可知，此时主变压器比率差动保护能够可靠动作。

由图A7（a）可知，当Rf1较大时，由于Ig1与Is1的幅值差较小，随着光伏电站并网容量的增加，A 相比率差动保护的灵敏度不断降低，最终出现m1_A小于制动系数整定值0.8 的现象。由图A7（b）可知，随着光伏电站并网容量由95 MV·A 增大至580 MV·A，m1_C先增大后减小。结合A、C 两相的比率差动保护动作情况可得，当光伏电站并网容量为580 MV·A时，比率差动保护存在拒动的风险。此时RSCR=3.95，意味着在交流系统仍为强系统时，比率差动保护便已存在拒动的风险。图A6、A7所示的仿真验证结果与理论计算结果基本一致，证明了理论计算的正确性。

以光伏电站并网容量为580 MV·A 为例，进一步分析在不同过渡电阻下光伏电站接入对主变压器比率差动保护的影响。将光伏电站侧替换为传统电源，其余参数保持不变，比较光伏电站接入和传统电源接入下主变压器比率差动保护的动作情况。表1为在不同过渡电阻取值下，光伏电站接入和传统电源接入时，m1_A与m1_C的变化规律及相应的比率差动保护动作情况。比率差动保护为相量值差动保护，其判据计算通常在1 个周期后进行，故下文表格中的差动电流与制动电流之比均为1个周期后的数据。

表1 光伏接入与传统电源接入情况下主变压器差动保护动作情况比较（情形1）Table 1 Comparison of main transformer action between PV access and traditional power supply access （Situation 1）

对比表1 中m1_A与m1_C的值可以看出，光伏电站接入和传统电源接入2 种情况下的A、C 相比率差动保护灵敏度均随着Rf1增大而下降，即比率差动保护的抗过渡电阻能力较弱。但光伏电站接入下的m1_A较传统电源接入情况下明显降低。当Rf1较小时，光伏电站接入下m1_C比传统电源接入时高，但随着Rf1的增大，m1_C的值迅速下降至0.8 以下。因此，结合A、C 两相比率差动保护的动作情况，可以得出主变压器比率差动保护存在拒动的风险。

4.2.2 情形2：主变压器低压侧出口处发生单相接地短路故障

以Rf2取1 Ω 和10 Ω 为例验证m2_A的变化规律，结果如附录A 图A8 所示。由图A8（a）可得，当Rf2较小时，由于Ig2与Is2的幅值差较大，因此光伏电站并网容量的增加对差动电流与制动电流相对大小的影响较弱，当并网容量大于等于375 MV·A 后，m2_A才存在小于0.8 的情况。由图A8（b）可得，当Rf2较大时，由于Ig2与Is2的幅值差较小，此时并网容量的增加对差动电流与制动电流的相对大小的影响较为显著，除并网容量为95 MV·A 的情况外，其他并网容量下的m2_A均小于0.8。图A8 所示的仿真验证结果与理论分析结果基本一致。

以光伏电站并网容量为480 MV·A 为例，比较光伏电站接入与传统电源接入时主变压器比率差动保护的动作情况，结果如表2 所示。此时，光伏电站接入下的m2_A不仅显著低于传统电源接入的情况，且在不同过渡电阻取值下，主变压器比率差动保护均出现拒动的情况。由于此时短路比RSCR=4.77，因此同样意味着在光伏电站接入的交流系统为强系统时，主变压器比率差动保护便已经存在拒动的可能。

表2 光伏接入与传统电源接入的主变压器比率差动保护动作情况比较（情形2）Table 2 Comparison of main transformer action between PV access and traditional power supply access（Situation 2）

另外，对比主变压器高压侧出口处发生单相接地短路故障的情况可知：由于主变压器低压侧出口处距离光伏电站更近，光伏电站并网容量的变化更容易影响比率差动保护的灵敏度及其动作的可靠性。

4.2.3 情形3：交流系统强度对比率差动保护的影响

本节以光伏电站额定容量为230 MV·A，低压侧发生单相接地短路故障为例，仿真验证不同短路容量比及过渡电阻下比率差动保护的动作情况，结果如附录B 表B3 所示。由表可以看出，比率差动保护的动作情况主要由光伏并网发电系统与交流系统的相对强弱决定。当短路容量比RSCR＜5 时，比率差动保护存在拒动风险。

由表2、B3可得，差动电流与制动电流之比存在小于0.5 的情况。由于比率制动系数的整定范围通常为0.5～0.8，当RSCR＞5时，可以在不改变主变压器比率差动保护原理的前提下，通过适当减小k提高比率差动保护的灵敏度；当RSCR＜5时，则需考虑增大交流系统强度以提高短路容量比，或进一步改进差动保护原理来提高差动保护的灵敏度和可靠性。

5 结论

本文基于光伏电站LVRT 期间的输出特性，对主变压器两侧出口处的单相接地短路故障进行了分析；并计及主变压器绕组接线方式，推导了差动电流与制动电流的比值表达式，进一步得出了光伏电站接入对主变压器比率差动保护的影响。所得主要结论如下：光伏电站的输出特性对主变压器比率差动保护的动作性能造成了一定影响；对比传统双端电源网络，主变压器比率差动保护抗过渡电阻能力更差；同时，受光伏电站与交流系统相对强弱的影响，主变压器比率差动保护的灵敏度变化显著，甚至存在较高的拒动风险；在不改变主变压器比率差动保护原理的前提下，可通过适当减小k、增大交流系统强度以提高短路容量比等措施，进而减小对光伏电站主变压器比率差动保护的影响。本文针对光伏电站主变压器比率差动保护的适应性分析，也为进一步改进主变压器差动保护原理提供了理论基础。

附录见本刊网络版（http：//www.epae.cn）。