例析数列不等式证明常用策略

丁 军

(山东省枣庄市第十六中学)

数列不等式证明是高考经常出现的一类问题,这类问题所涉及的知识点较多,对学生知识的灵活运用有一定的要求.为帮助学生更加系统、全面地了解相关问题及解题策略,本文结合实际问题详细进行介绍,以提升学生数学学科核心素养.

1 函数法

数列作为一类特殊的函数,具有函数相应的性质.因此,在解答数列不等式问题时,学生可以借助函数法进行解答,通过构造函数利用函数的单调性、极值等证明不等式.在实际的解题中,函数法通常运用于变量与常数之间的比较,因此在解题中需要将不等式转化为仅一侧含变量,并构造函数,利用函数的性质求其最值,最后将最值与常数项进行比较.

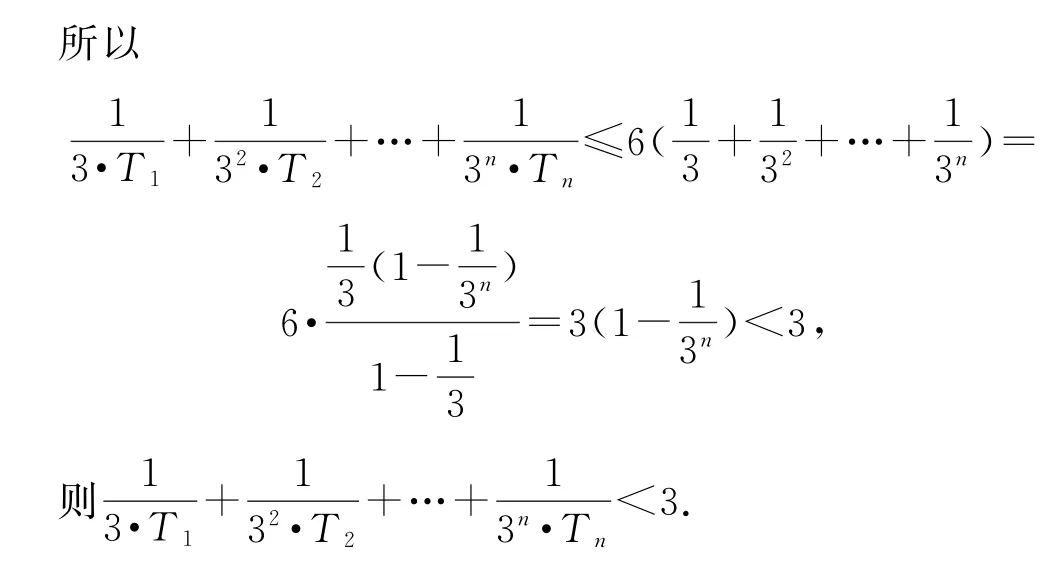
本题先对数列不等式进行变形,再构造函数利用函数的单调性证明数列不等式.

2 放缩法

放缩法是证明数列不等式过程中常用的方法,通过将不等式的一侧进行适当放大或缩小,从而证明原不等式成立.在实际运用中,先将要证明的不等式的一侧进行适当放大或缩小,再将其与另一侧进行比较,最后根据传递性确定不等式成立.

例2 数列{an}的前n项和为Sn,满足2Sn＝an＋1－2n＋1＋6(n∈N∗),且a1,a2＋5,a3成 等 差数列.

(1)求数列{an}的通项公式;

(2)证明:对于一切正整数n,有

本题结合数列不等式特点,将其进行合理变形,而后借助不等式常见性质进行放缩.

3 归纳法

利用归纳法在解答数列不等式时,要先对问题进行分析,结合已知条件证明当n＝1时,不等式成立;而后假设当n＝k时,不等式成立,进一步验证当n＝k＋1 时,不等式成立;最后进行归纳,证明不等式成立.

在运用归纳法进行解题时,需要学生全面理解掌握其解题步骤与要求,从而才能保证答案的准确性.

4 比较法

比较法是证明不等式问题时一种比较直接的方法,即对不等式进行整理、转化,而后将不等式两侧进行作差、作商,通过差、商与0,1之间关系的比较,从而证明不等式.

例4 已知等差数列{an}前n项和为Sn,a1＝1,且S1,S2,S3＋3成等比数列.

(1)求{an}的通项公式;

(2)若{an}单调递增,证明:

巧妙地运用作差、作商的方法有时可以较快地对数列不等式进行证明,但有时需要将其与放缩法进行结合.

综上,数列不等式证明问题有多种解法,在实际的运用中,学生应当结合题目信息,灵活选择、运用解题策略,从而提升解题效率.

(完)