小议一元二次方程根的判别式的作用

王兴涛 于志东

(山东省青州第一中学)

一元二次方程ax2＋bx＋c＝0(a≠0)根的判别式为Δ＝b2－4ac.

当Δ＝b2－4ac＞0时,方程有两个不相等的实数根

当Δ＝b2－4ac＝0时,方程有两个相等的实数根

当Δ＝b2－4ac＜0时,方程无实数根.

这是初中学习过的,在高中数学解题中常常用到,主要作用有以下九种.

1 求解函数的定义域问题

由于函数f(x)是二次根式的形式,被开方式需大于或等于零,因此将问题转化为求解x2＋2ax－a≥0,进而用判别式Δ≤0求解.

2 求解存在性问题

例2 若命题“存在x0∈R,使得x20＋(a－1)x0＋1＜0”是真命题,则实数a 的取值范围是________.

因为“存在x0∈R,使得x20＋(a－1)x0＋1＜0”是真命题,所以Δ＝(a－1)2－4＞0,解得a＜－1 或a＞3,故实数a的取值范围是(－∞,－1)∪(3,＋∞).

含有量词的命题的真假性判断是高考的重点题型.本题欲求存在实数x使得不等式x20＋(a－1)x0＋1＜0成立,只需求解Δ＞0.

3 求解恒成立问题

例3 在R上定义运算⊗:x⊗y＝x(1－y),若不等式(x－a)⊗(x＋a)＜1对任意实数x恒成立,则实数a的取值范围是_________.

因为(x－a)⊗(x＋a)＜1,所以(x－a)(1－x－a)＜1,即x2－x－a2＋a＋1＞0在R 上恒成立,所以Δ＝4a2－4a－3＜0,解得故实数a的取值范围是

高考数学创新题型是通过给出一个新概念、约定一种新运算或给出几个新模型来创设全新的问题情境.解答这类创新问题有三种方式:一是通过转化,化“新”为“旧”;二是通过深入分析,多方联想,以“旧”攻“新”;三是创造性地运用数学思想方法,以“新”制“新”.

4 求解函数的零点问题

例4 当m＝_____时,f(x)＝x2＋2mx＋3m＋4的两个零点均比－1大.

解得－5＜m＜－1,故当－5＜m＜－1时,f(x)的两个零点均比－1大.

若函数f(x)＝ax2＋bx＋c(a＞0)的零点均大于m,则

5 求最值问题

例5 已知实数a,b,c满足a＋b＋c＝0,a2＋b2＋c2＝1,则a的最大值为_________.

由于问题是求a的取值范围,因此把2b2＋2ab＋2a2－1＝0看作是关于b的一元二次方程,再用根的判别式求解.

6 求解圆锥曲线的关系问题

例6 已知抛物线和椭圆的方程分别为y2＝2mx＋5m,3x2＋4y2＝12,当m＝_________时,抛物线与椭圆相切.

将抛物线的方程代入椭圆的方程可得3x2＋8mx＋4(5m－3)＝0,则

求解本题时将曲线的交点个数转化为一元二次方程的根的个数,进而由Δ的正负可确定一元二次方程的根的个数.

7 求解数列问题

例7 若实数a1,a2,a3,a4满足(a21＋a22)a24－2a2(a1＋a3)a4＋a22＋a23＝0.求证:a1,a2,a3成等比数列,且公比为a4.

把已知条件看作关于a4的一元二次方程,则

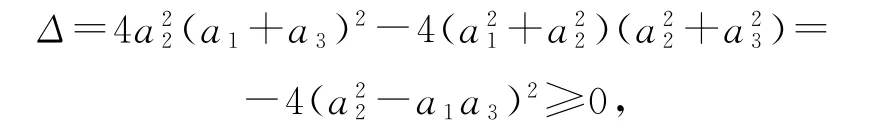
所以a4是数列a1,a2,a3的公比.

求解本题时把已知条件看作关于a4的一元二次方程,由根的判别式来确定a1,a2,a3之间的关系.

8 求解集合间的关系问题

例8 设集合A＝{x|x2－3x＋2＝0},B＝{x|x2＋2(a＋1)x＋(a2－5)＝0},若A∪B＝A,则实数a的取值范围是( ).

因为A∪B＝A,所 以B⊆A,因 为B＝{x|x2＋2(a＋1)x＋(a2－5)＝0},所以

当Δ＜0,即a＜－3时,B＝∅,满足条件.

当Δ＝0,即a＝－3时,B＝{2},满足条件.

当Δ＞0,即a＞－3时,只有B＝{1,2}满足条件.

综上,实数a的取值范围是a≤－3.

集合间的关系问题,一般是把集合化简,由于A∪B＝A,则B⊆A,故需对方程x2＋2(a＋1)x＋(a2－5)＝0根的情况进行讨论.

9 求函数表达式问题

分段函数是重要的函数类型,求解时要注意各个区间上的解析式的对应.

(完)