低值易耗品采购预算的成本预测模型研究——以L学院为例

武学志,詹竞舟

(兰州职业技术学院 国资及产业管理处, 甘肃兰州730070)

党的十八大以来,国家极为注重建设资源节约型和环境友好型社会。2021年7月,国家发展和改革委员会发布的《“十四五”循环经济发展规划》提出了新的目标,即到2025年,我国将基本建立资源循环型产业体系,建成全社会的资源循环利用体系,主要资源产出率比2020年提高约20%,单位国内生产总值的能源消耗和用水量比2020年分别降低13.5%和16%左右。这些明确的目标对经济社会的可持续发展提出了更高的要求[1]。节约资源不仅是发展生产力的有效手段,同时也是有效的环境保护措施,是统筹人与自然和谐发展的重要举措。

一、研究意义

低值易耗品是指单项价值在规定限额以下并且使用期限不满一年、能多次使用而基本保持其实物形态的劳动资料[2]。笔者通过对近几年L学院低值易耗品采购、使用情况的分析,发现低值易耗品的种类不断扩大,消耗量逐年上升,造成低值易耗品采购预算随之不断增加。这对L学院的高水平、高质量建设和深化资源整合产生了一定的影响;同时,也未能达到资源节约型社会建设与发展的要求。在此背景下,本文通过对L学院部分有代表性的低值易耗品采购、使用数据的分析,提出一套低值易耗品采购成本的预测模型。该预测模型能够优化和控制低值易耗品采购预算规模,节约经费开支,有效降低资源消耗,符合国家建设资源节约型社会的总体要求。

二、存在问题

低值易耗品采购预算与实际采购、使用存在以下关系:低值易耗品的采购预算一般是根据历史数据编制,但在执行过程中,实际支出可能会高于或低于预算。

(一)低值易耗品采购预算与实际追加之间的矛盾

预算是实际采购的基础和指导,对低值易耗品实际采购的规模和结构起着重要的引导作用。在实际使用过程中,由于低值易耗品不断消耗灭失,在需要增补的情况下,追加预算就是一个不断调整和完善的过程,以确保低值易耗品使用的合理性和经济性。

(二)低值易耗品预算与实际采购、使用之间的矛盾

一方面,预算的编制是基于历史使用数据和市场趋势的分析,可能存在预测偏差和不确定性,导致实际使用量与预算存在一定偏差。另一方面,采购会受到多种因素的影响,如供应情况、市场变化、需求波动等,这些因素可能导致在实际使用量未发生明显变动的情况下采购超出预算范围。

因此,从采购源头做好对低值易耗品采购预算的预测显得至关重要。一是加强对预算和采购的双向数据分析和监控,建立有效的数据采集和分析机制,随时监测采购数据,发现问题并及时进行干预。二是对低值易耗品使用数据进行统计学分析,设计科学的预测模型,预测未来采购趋势,以提高预算的准确性和有效性,节约经费开支。

三、研究方案

研究以L学院部分有代表性的低值易耗品的使用需求、采购规模和消耗量等数据集合作为数据分析基点,运用统计定量分析中贝叶斯方法和Python语言实现等方法,在质量和技术层面进行客观数据解析,建立初步预测模型,并开展实证分析。

(一)贝叶斯方法

贝叶斯方法是一种基于概率论的统计推断方法,可以用于低值易耗品需求概率推断和预测分析。下面简要介绍如何使用贝叶斯方法来实现这一目标。

1.确定先验概率分布

先验概率分布是指在没有任何数据的情况下,对需求的概率分布的预估。先验概率分布可以基于以往经验或行业标准等因素来确定。

2.收集低值易耗品需求数据

这些数据包括历史采购记录、一年的需求量和实际使用量、使用频率、库存数量等。这些数据将用于计算后验概率分布。

3.计算后验概率分布

使用贝叶斯定理,根据先验概率分布和收集到的数据,计算出新需求的概率分布。这个过程可以使用贝叶斯公式来实现:

P(需求|数据)=P(数据|需求)×P(需求)/P(数据)

其中,P(需求|数据)是后验概率分布,P(数据|需求)是似然函数,P(需求)是先验概率分布,P(数据)是归一化常数[3]。

4.需求概率评估

在确定后验概率分布的基础上,对需求的概率分布进行重新估计,例如计算出需求量的期望值、方差、置信区间等,来帮助决策者制订相关方案。

(二)建模机理

在研究过程中使用贝叶斯方法对概率分布进行建模,用所采集的一定量低值易耗品采购、使用数据更新概率分布,以确保结果的准确性。在应用贝叶斯方法进行决策分析时,需要充分考虑数据的可用性和真实质量,以及对概率分布的准确建模。

(三)建立贝叶斯随机效应模型

1.模型构建

(1)分析数据

分析低值易耗品的采购、使用数据,包括需求量、采购量、使用量、库存量、报废量、成本等信息。

(2)设计先验分布

通过对历史数据的分析,确定每种低值易耗品的需求、采购、使用的概率分布,作为先验分布。

(3)设计似然函数

似然函数是观测数据在给定参数下的概率分布。根据数据的不同特点,选择合适的似然函数进行建模。

(4)贝叶斯推断

根据先验分布、似然函数和观测数据,利用贝叶斯定理计算出后验分布,即在给定观测数据的情况下参数的概率分布。

2.开展模型预测和决策分析

通过使用后验分布,计算出低值易耗品的需求量、采购量、使用量等信息的概率分布,进行预测和决策分析。

3.模型评估和优化

对模型进行评估,检验其对数据的拟合程度和预测能力,以及模型的稳健性。如果模型存在问题,可以进行参数调整、模型优化等操作,提高模型预测的准确性。

建立贝叶斯随机效应模型能够更直观地展示低值易耗品的采购、使用情况,预测未来使用数量,制订更合理的采购预算和采购计划。

(四)Python语言实现低值易耗品贝叶斯预测步骤

1.确定先验分布;

2.对低值易耗品的历史数据整理入库;

3.计算后验分布;

4.利用后验分布,优化算法,输出预测。

(五)制订研究路径

通过上述方案制订研究路径(见图1)。

图1 研究实施路径图

四、实例分析

(一)先验概率分布

为了进行概率推断和决策分析,需要设定一个关于低值易耗品的先验概率分布。研究选取L学院2022年采购的部分低值易耗品作为实例:A型号硒鼓、B型号硒鼓、A4复印纸、5号电池、活页笔记本、拖把、中性笔、插线板和档案袋。假设每种低值易耗品的需求量都是独立的,表示为需求量,并且根据以往需求和采购数据已知的正态分布,设定每种低值易耗品的需求量的先验概率分布(见表1)。

表1 2022年L学院部分低值易耗品先验概率分布

这些先验概率分布反映了当没有以往低值易耗品的需求量信息时,对需求量的不确定性的估计。

(二)选取复印纸的观测数据更新其验后概率分布

假设上述A4复印纸的实际需求量为D,其先验概率分布为P(D),实际观测数据包括需求量为2505包、采购量为3040包、使用量为2748包。我们可以用贝叶斯定理表示为:

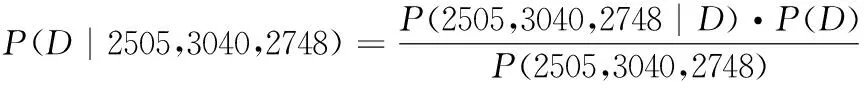
(1)

其中,P(2505,3040,2748|D)表示在给定需求量为D的情况下,观测到需求量为2505、采购量为3040、使用量为2748的概率,这里通过先前给定的复印纸需求模型进行计算。P(D)表示复印纸需求量为D的先验概率分布,研究者已经给定。P(2505,3040,2748)表示观测到需求量为2505、采购量为3040、使用量为2748的概率,可以通过边缘化计算:

(2)

(三)后验概率分布

观测到实际数据后,用贝叶斯定理来更新先验概率分布,得到后验概率分布。具体来说,假设研究者观测到复印纸的需求量为D,采购量为P,使用量为U,则复印纸需求量的后验概率分布可以表示为:

P(D|P,U)=frac{P(P,U|D)P(D)}{P(P,U)}

(3)

在这里,P(P,U|D)表示在给定需求量为D的情况下,观测到采购量为P、使用量为U的概率;P(P,U)表示观测到采购量为P、使用量为U的概率。

(四)期望值、方差和置信区间

根据复印纸的后验概率分布,计算复印纸需求量的期望值、方差和置信区间。

1.计算复印纸需求量的期望值(也就是均值)

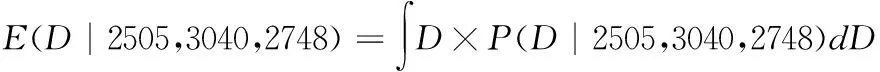
(4)

使用数值积分的方法计算上式,得到:

E(D|2505,3040,2748)≈2788.08

即复印纸需求量的期望值约为2789包。

2.计算复印纸需求量的方差

Var(D|2505,3040,2748)=

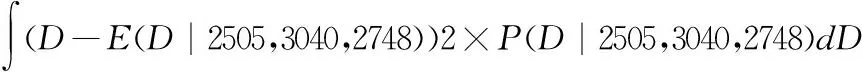
(5)

同样使用数值积分的方法计算上式,得到:

Var(D|2505,3040,2748)≈312768

即复印纸需求量的方差约为312,768。

3.计算复印纸需求量的置信区间

假设我们希望计算95%的置信区间,那么根据后验概率分布,我们可以分别找到需求量D1和D2,使得:

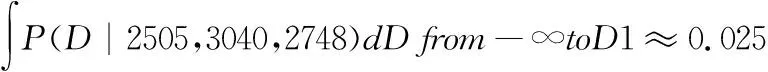
(6)

(7)

其中D1和D2分别表示置信区间的下界和上界,这里的0.025对应于置信水平为95%时的两个尾部概率(因为对称性,左右两侧的概率都是0.025)。

通过数值积分的方法,可以得到:

D1≈2630.72

D2≈2841.49

即95%的置信区间为[2630.72,2841.49]。这意味着在给定观测数据的情况下,我们有95%的置信水平相信复印纸的实际需求量在这个区间内。

五、Python应用分析

(一)以复印纸数据建立Python应用程序模块

1.根据输入先验分布的均值输出概率密度图、后验分布均值和后验分布标准差

使用Python编写如下代码:

import numpy as np

import scipy.stats as stats

# 设置先验分布的均值和标准差

prior_mean = 2505

prior_std = 243

# 摸底需求量、实际采购量和实际使用量

demand = 2505

purchased = 3040

used = 2748

# 计算后验分布的均值和标准差

post_mean = (prior_mean/prior_std**2 + used/demand) / (1/prior_std**2 + 1/demand)

post_std = np.sqrt(1 / (1/prior_std**2 + 1/demand))

# 打印后验分布的均值和标准差

print("后验分布均值: {:.2f}".format(post_mean))

print("后验分布标准差: {:.2f}".format(post_std))

# 生成概率密度函数

x = np.linspace(post_mean - 4*post_std, post_mean + 4*post_std, 1000)

pdf = stats.norm.pdf(x, post_mean, post_std)

# 绘制概率密度函数图像

import matplotlib.pyplot as plt

plt.plot(x, pdf)

plt.title('复印纸需求概率分布(正态分布)')

plt.xlabel('复印纸需求量')

plt.ylabel('概率密度')

plt.show()

运行上述程序,Python将数据输出为图2形式。

图2 Python输出概率密度图

并得出后验分布均值:2738.11,后验分布标准差:49.02

2.利用Python语言实现基于贝叶斯方法的复印纸采购预测程序

编写代码如下:

import numpy as np

from scipy.stats import norm

# 先验概率分布

prior_mean = 2505

prior_std = 243

prior_dist = norm(prior_mean, prior_std)

# 观测数据

demand = 2505

purchase = 3040

usage = 2748

# 计算边缘化概率

def marginal_prob(demand_dist):

return np.trapz(demand_dist.pdf(np.linspace(0, 3000000, 10000)))

# 计算后验概率分布

def posterior_dist(demand_dist):

demand_likelihood = norm(demand_dist.mean(), 100000).pdf(demand)

purchase_likelihood = norm(demand_dist.mean() + 200000, 100000).pdf(purchase)

usage_likelihood = norm(demand_dist.mean() - 160000, 100000).pdf(usage)

numerator = demand_likelihood * purchase_likelihood * usage_likelihood * demand_dist.pdf(

np.linspace(0, 3000000, 10000))

denominator = marginal_prob(demand_dist)

return numerator / denominator

# 计算期望值、方差、置信区间

def calc_stats(posterior):

mean = np.trapz(posterior * np.linspace(0, 3000000, 10000))

var = np.trapz(posterior * (np.linspace(0, 3000000, 10000) - mean) ** 2)

conf_int = norm.interval(0.95, loc=mean, scale=np.sqrt(var))

return mean, var, conf_int

# 运行程序

prior = prior_dist.pdf(np.linspace(0, 3000000, 10000))

posterior = posterior_dist(prior_dist)

demand_likelihood = norm(prior_dist.mean(), 100000).pdf(demand)

purchase_likelihood = norm(prior_dist.mean() + 200000, 100000).pdf(purchase)

usage_likelihood = norm(prior_dist.mean() - 160000, 100000).pdf(usage)

mean, var, conf_int = calc_stats(posterior)

# 输出结果

print(f"Prior mean: {prior_dist.mean():,.2f}")

print(f"Prior std: {prior_dist.std():,.2f}")

print(f"Demand likelihood: {demand_likelihood:.4f}")

print(f"Purchase likelihood: {purchase_likelihood:.4f}")

print(f"Usage likelihood: {usage_likelihood:.4f}")

print(f"Posterior mean: {mean:,.2f}")

print(f"Posterior std: {np.sqrt(var):,.2f}")

print(f"95% confidence interval: {conf_int[0]:,.2f} - {conf_int[1]:,.2f}")

该程序使用了scipy库中的norm函数来表示正态分布,并使用numpy库中的trapz函数进行积分计算[4]。在程序中,首先定义了先验概率分布,输入观测数据;其次定义了三个观测数据的似然函数,使用贝叶斯公式计算出后验概率分布;最后使用后验概率分布计算出了期望值、方差和置信区间,并将结果输出到控制台。

(二)部分低值易耗品Python语言编写应用程序模块

以A型号硒鼓、B型号硒鼓、A4复印纸、5号电池、活页笔记本、拖把、中性笔、插线板和档案袋为实例的Python应用分析。

1.利用Python语言实现计算基于贝叶斯方法的低值易耗品采购置信区间

编写代码如下:

import numpy as np

from scipy.stats import norm

#定义物品及其参数

items = ["A型号硒鼓", "B型号硒鼓", "A4复印纸", "5号电池", "活页笔记本", "拖把", "中性笔", "插线板", "档案袋"]

means = []

stds = []

#手动输入均值和标准差

for item in items:

mean = float(input(f"请输入{item}的平均值:"))

std = float(input(f"请输入{item}的标准差:"))

means.append(mean)

stds.append(std)

#手动输入观测数据

observations = []

for i in range(len(items)):

demand = int(input(f"请输入{items[i]}的需求量:"))

purchase = int(input(f"请输入{items[i]}的采购量:"))

usage = int(input(f"请输入{items[i]}的使用量:"))

observations.append((demand, purchase, usage))

#定义置信水平

confidence = 0.95

#计算置信区间

for i in range(len(items)):

demand, purchase, usage = observations[i]

#计算先验分布的参数

prior_mean = means[i]

prior_std = stds[i]

#计算后验分布的参数

posterior_mean = (prior_mean / prior_std ** 2 + usage) / (1 / prior_std ** 2 + usage / purchase)

posterior_std = np.sqrt(1 / (1 / prior_std ** 2 + usage / purchase))

#计算置信区间

lower, upper = norm.interval(confidence, loc=posterior_mean, scale=posterior_std)

print(f"{items[i]}的需求量置信区间为:[{lower:.2f}, {upper:.2f}]")

在Python语言编写的实用程序中,第一步输入了每种低值易耗品的先验分布,即在不考虑实际观测数据的情况下对需求量的预估。第二步通过观测数据来计算每个低值易耗品的后验分布,以此来更新对需求量的估计。总体来说,将观测数据代入每种低值易耗品的先验分布中,得到对观测数据的似然函数,进而将这些似然函数与先验分布相乘,得到后验分布。后验分布是在考虑了实际观测数据的情况下对需求量的新估计,是对需求量的最新认识。第三步通过后验分布计算需求量的期望值、方差和置信区间。这些统计量提供了对需求量的置信度度量,具体表示出期望值反映了对需求量的中心估计,方差反映了对需求量的分散程度,置信区间提供了对需求量的置信度范围。

2.实用程序输出的部分低值易耗品预算预测分析

通过Python语言编程实现的部分低值易耗品预测数据,可以将采购预算较为准确地控制在95%置信区间内,该区间内的采购预算相较原先采用经验估算的采购预算,能够针对不同种类的低值易耗品节约3%～36%范围之间不等的预算(见表2),即为部分低值易耗品Python编程输出的置信区间数据和预算节约比例。

表2 部分低值易耗品预算预测表

六、研究结果

研究以L学院部分有代表性低值易耗品为例,通过贝叶斯方法进行使用趋势分析和采购预算预测。根据历史数据和先验概率分布,使用Python语言编写代码计算低值易耗品需求量的期望值、方差和置信区间。在此基础上,制订有针对性的采购计划和采购策略,从而实现有效提高低值易耗品使用效率,调节采购预算的目的。

(一)模型优点及局限性

1.模型的优点

(1)贝叶斯方法考虑到了不确定性,因此可以更好地应对现实世界中不确定性和复杂性带来的挑战;

(2)通过迭代更新先验概率,能够更好地理解和解释数据;

(3)使用先验知识,如历史数据和专家知识等,以提高模型的准确性和可靠性;

(4)可以应用于各种不同类型的数据,包括二元数据、连续数据和分类数据等;

(5)虽然贝叶斯方法在数据量较大的情况下的计算成本很高,但通过GPU等并行加速运算设备,实现了对大批量数据的高效计算。

2.模型的局限性

(1)贝叶斯方法需要有一个合适的先验概率分布,这可能需要一些主观判断和领域知识;

(2)贝叶斯方法需要一些专业技能和统计知识,以便正确地应用和解释结果;

(3)在贝叶斯分析中,不同的先验分布会导致不同的后验分布。因此,先验分布的选择可能对结果产生较大的影响。

(二)结论和展望

本研究采用基于Python语言实现贝叶斯方法的低值易耗品采购预算预测程序,对低值易耗品需求量进行了概率推断和决策分析。通过对历史数据和先验知识进行建模,进而得到了低值易耗品需求量的后验概率分布,为采购部门提供了重要的预算参考信息。

在未来的研究中,笔者将进一步探讨如何将此基础模型通过Python开展更多历史数据的训练,积累迭代升级,以提高预测准确度。同时,考虑将该模型应用于实时预测和调整,以更好地满足采购单位的需求。笔者相信,通过不断的研究和实践,该模型将为采购管理提供更加精确和有力的支持。