基于改进U-Net模型的次季节降水预报订正

潘 乐，郑子华，游立军，翁 彬

(1.福建师范大学计算机与网络空间安全学院，福建 福州 350117；2.数字福建大数据安全技术研究所，福建 福州 350117；3.福建省公共服务大数据挖掘与应用工程技术研究中心，福建 福州 350117；4.福建省气象信息中心，福建 福州 350025；5.福建省灾害天气重点实验室，福建 福州 350025)

随着社会和经济的发展，人们对高质量天气预报的需求也在不断增长，数值预报模式是天气预报业务的主流方法，但是由于初始条件误差和模式分辨率不高等原因，预报结果一直存在误差[1].我国南部大陆地区受东亚夏季风影响，雨量充沛，年降水量800 mm以上，提升我国南部大陆降水预报的准确性，对该地区人民生命安全和国家经济建设具有积极作用.

本研究主要关注次季节尺度的降水预报订正，在这个时间段上，来自大气初始状态的可预报性逐渐减弱，而大气对外强迫的响应还未形成，预报结果具有较大不确定性.数值模式会通过初始条件扰动生成多个预报结果，以描述降水预报的不确定性，称为集合预报[2].不过由于大气是混沌系统[3]，数值模式发展到今天仍然无法反映真实的大气状态，模式预报结果也就存在着不可避免的误差.所以对模式预报结果进行订正，提高预报技巧是十分有必要的[4].

近10年来，深度学习发展迅速，在计算机视觉和自然语言处理等领域都取得了很大的成就.深度学习技术在非线性关系拟合和空间相关性建模等方面，相对于气象领域的传统方法有着很大的优势，将深度学习技术应用到气象问题，有很大的潜力.本研究结合深度学习技术和次季节降水预报订正的特点，提出了一种新的次季节降水预报订正方法，可以有效降低模式预报误差并生成降水概率预报.

本文主要贡献如下：(1)将U-Net模型应用到次季节降水概率预报订正，设计了一种新的次季节概率预报订正方法；(2)结合问题实际情况，改进U-Net模型，为次季节降水预报订正任务设计了CPF-Net(calibrated probabilistic forecast net)模型；(3)针对降水数据特点，设计了动态加权的损失函数，提高了强降水预报性能.

1 相关工作

为了校正数值模式预报结果中的偏差，有经验订正(analog)[5]、频率匹配法[6]和分位数回归[7]等非参数方法，这些方法使用简单，可以在一定程度上消除误差，但是无法保证结果的可靠性，同时也无法生成降水概率分布.集合模式输出统计(ensemble model output statistics，EMOS)[8]是概率预报订正的代表方法，先假定预报变量的概率分布，然后通过建立预报变量和概率分布参数的函数关系，求解连续概率分布函数，比如使用非均匀回归(non-homogeneous regression，NHR)预测正态分布的均值和方差[9].另一种生成概率预报的方法基于联合概率模型(joint probability model，JPM)[10]，通过拟合预报变量和观测值之间的二维概率分布来建立.也有方法不对降水量分布进行假设，比如使用随机森林等机器学习方法预测降水量的分位数[11]，或者以降水量超过某一阈值的概率作为输出[12].以上这些方法虽然已经取得了较好的效果，但都没有利用数据中的空间信息.

基于深度学习的方法在空间信息的提取上具有很大优势，气象领域在深度学习技术上也进行了很多讨论[13].在20世纪末，就有学者将人工神经网络(artificial neural network，ANN)应用到预报订正任务中[14].目前深度学习中的许多经典网络结构都被应用到预报订正领域.比如Dupuy等[15]将U-Net模型应用到云量预报的订正；Zhang等[16]基于长短期记忆神经网络(long short term memory network，LSTM)[17]构建了我国东部地区12 h不同量级的降水预报订正模型.也可以将深度方法与传统方法相结合，比如使用深度学习技术和分位数回归方法结合，使用神经网络得到对分位数函数的近似值[18].目前，深度学习技术在气象领域已经有了很多应用，但基于深度学习的次季节降水预报订正研究还很少，在使用U-Net模型进行次季节降水预报订正的研究[19]，只使用了原始的U-Net模型，没考虑降水分布的特点，使用正态假设的均方根误差作为损失函数，没有生成降水概率分布.深度学习在次季节降水预报订正这个领域的应用潜力还有待进一步开发.

2 研究方法

本文对集合预报的成员均值进行订正，生成订正后的降水量概率分布.首先求集合预报的成员均值，然后对均值进行指数变换，从而可以使用正态分布对数据建模.然后对U-Net模型进行调整，使之能够应用到本文研究的问题中.再针对次季节降水预报问题特点，结合残差网络和通道注意力机制改进U-Net模型，得到CPF-Net模型.最后为了避免数据不平衡影响模型性能，设计了损失函数动态加权方案，优化模型训练过程.

2.1 数据变换

原始的降水数据属于非正态数据，无法使用常见的正态分布进行建模.可使用指数变换将降水数据变换到正态分布，再使用正态分布对降水数据进行建模.u和v分别表示预报降水量和观测降水量：

x=up，y=vp，

(1)

其中，x表示变换后的预报数据，y表示变换后的观测数据，均服从正态分布，p是变换参数.假设变换后的原始预报x和观测数据y满足二维正态分布：

(2)

其中，μx和σx表示x的均值和方差，μy和σy表示y的均值和方差，ρ为x和y的相关系数.p、μx、σx、μy、σy和ρ均为未知参数，可以通过极大似然估计法求得.根据二维正态分布，可得y的条件概率服从正态分布：

(3)

于是可以通过深度学习模型预测正态分布的均值和方差，得到订正后的降水量连续概率密度.

本文使用数据变换后的集合预报的集合均值作为模型输入，集合均值通常包含了集合预报中的大部分信息[20]，不同格点的数据进行不同的指数变换.模型输出正态分布的均值和方差，每个格点都会输出一组均值和方差.

要得到超过某一降水量阈值的降水事件发生的概率，需要对降水量进行指数变换，然后将变换后的值带入到正态分布中计算发生概率，零值也是相同的处理方式.要得到订正后的集合预报，需要先对正态分布进行采样，然后将负值赋值为零，再通过指数变换的逆变换进行数据还原，得到订正后的集合预报结果.无降水事件发生的概率，实际是正态分布中，降水量小于零的概率，在产生集合预报时，将小于零的采样结果赋值为零.集合预报均值变换前后的数据频率分布如图1所示，可以看出数据变换前的降水量频率分布明显不符合正态分布，而变换后的频率分布则基本符合正态分布.

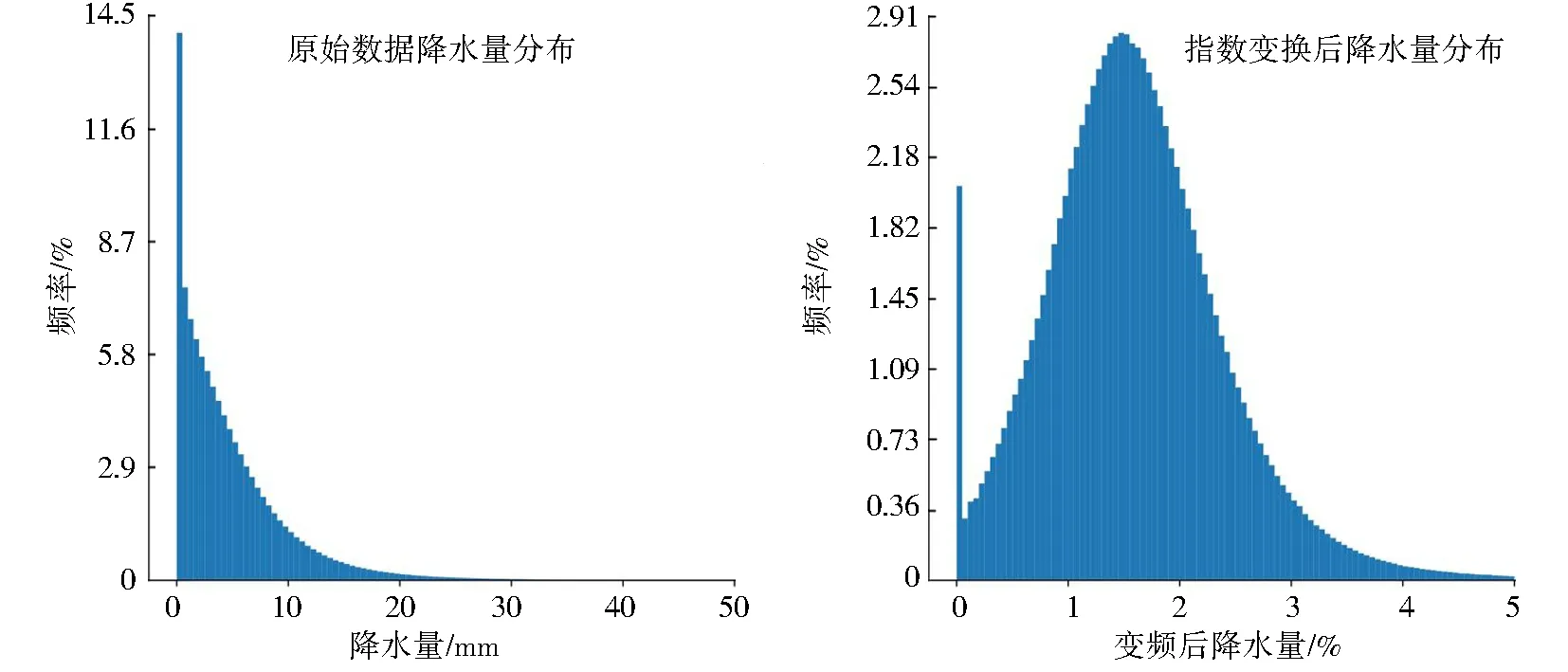
图1 数据变换前后分布对比Fig.1 Comparison of data distribution before and after conversion

2.2 U-Net模型结构

U-Net模型[21]最早是在医学图像分割中被提出，后来也应用在很多气象任务中.本文以U-Net模型为基础，针对数据具体情况对U-Net模型进行调整，最终实现的U-Net模型结构和数据形状变化如图2所示.由于输入数据尺寸较小，无法进行4次下采样操作，将U-Net模型中的下采样减少为2次.因为数据集较小，模型训练时容易过拟合，模型通道数调整到如图2所示，减少模型参数.

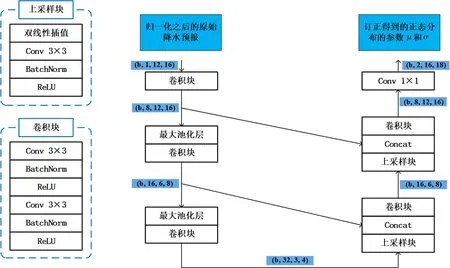
图2 U-Net模型结构Fig.2 Structure of the U-Net model

2.3 CPF-Net模型结构

针对次季节降水预报具体情况，本文基于U-Net改进设计了CPF-Net模型，模型具体结构如图3所示.次季节降水预报订正是对30 d的预报结果进行订正，随着提前期的增加，误差模式可能会随之变化.于是引入通道注意力机制，结合时间嵌入思想，将提前期广播到和输入数据相同维度，然后经过一个简单的卷积神经网络，得到通道权重，与CPF-Net对应层提取的特征相乘，得到每个提前期特有的特征.

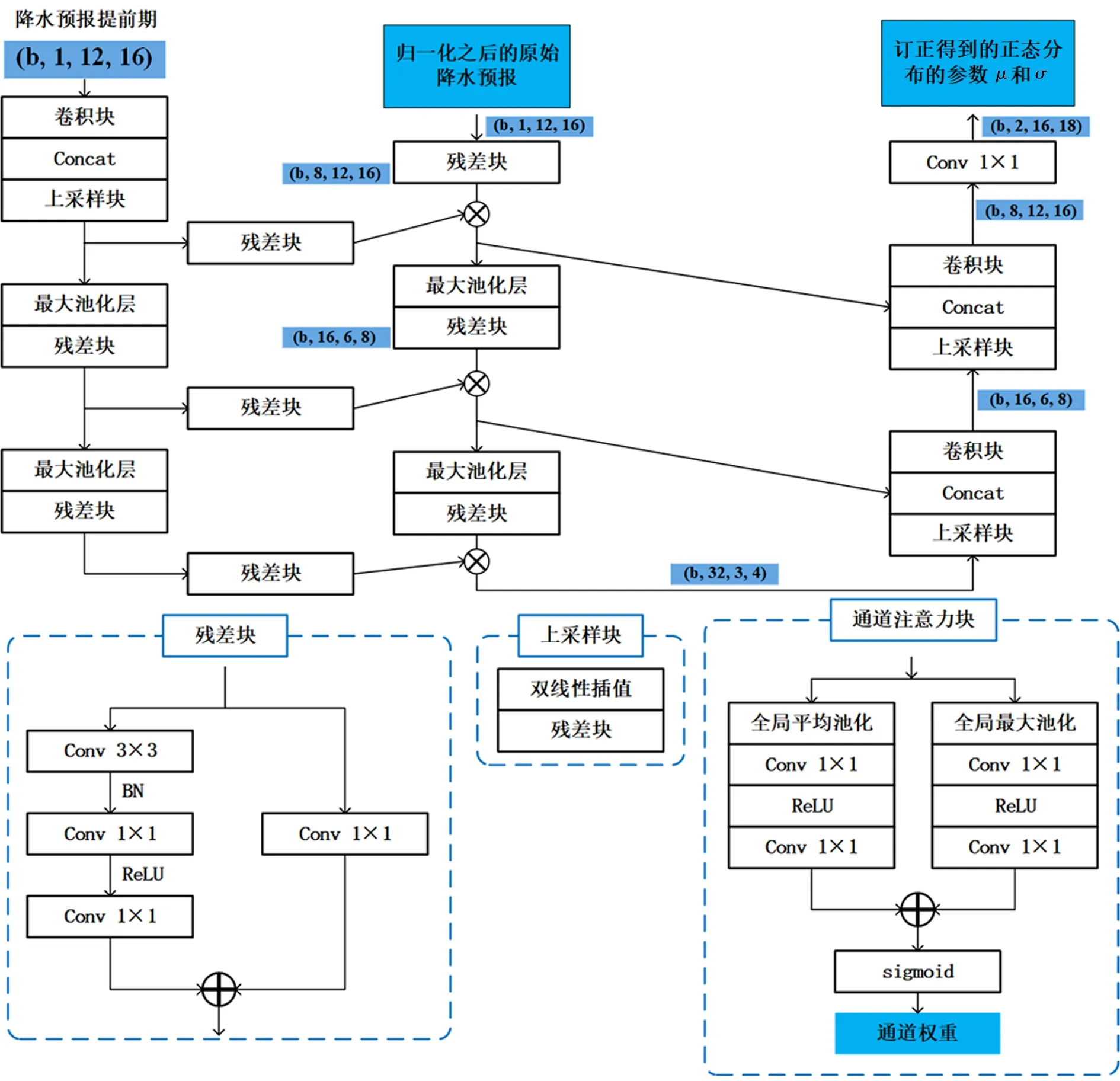
图3 CPF-Net模型结构Fig.3 Structure of the CPF-Net model

次季节降水预报订正原本可使用的训练数据就较少，引入通道注意力机制后模型更容易过拟合，于是在模型中引入残差块，代替原本的卷积块.Res-Net[22]在深度神经网络中引入残差连接，在图像分类任务中取得了巨大的成功，已经被证明可以有效降低模型过拟合风险，同时提升模型学习能力.引入残差块后，即使模型相对于原始的U-Net更加复杂，也不会发生过拟合问题，订正效果反而更好.

2.4 损失函数

CRPS(continuous ranked probability score)可以衡量连续概率分布与确定性观测结果之间的差异，计算公式如下：

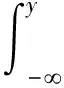
(4)

使用正态分布对降水数据进行建模，计算正态分布与指数变换后的标签值之间的误差，损失函数的解析公式为[9]：

(5)

其中，y表示模型输入对应的标签值，Fμ，σ为均值为μ，方差为σ正态分布的分布函数，F(·)表示标准正态分布的分布函数，f(·)表示标准正态分布的概率密度函数.

降水数据本身带有严重的数据不平衡问题，数据中弱降水事件占据大部分.不平衡的训练数据使得训练出的模型会偏向预测较小的降水量，对强降水事件估计不足.对数据不平衡问题，损失函数加权是常用的做法，包含权值的损失函数如式(6)所示：

Loss=weight×CRPS(Fμ，σ，y).

(6)

不同的降水量需要对应不同的权重，数据偏斜程度的不同也会影响权重的设计，这导致一个合适的权重设计往往需要非常多次的尝试.针对这个问题，本文设计了损失函数动态加权方案，根据标签值y计算权重，pow为需要人工调试的超参数，动态权重weight的计算方式如式(7)所示：

weight=(y+1)pow，

(7)

pow可以针对数据不平衡的程度进行灵活调整，当pow为0时，损失函数就是式(5)，pow越大，强降水格点获得的权重就会越大.

3 实验

3.1 数据集

本文研究区域为我国南部地区(22°-34°N，103°-123°E)，对提前期30 d内的模式预报结果进行订正.降水预报数据为欧洲中期天气预报中心(European Centre for Medium-range Weather Forecasts，ECMWF)的次季节到季节(sub-seasonal to seasonal，S2S)预测项目提供的回报数据.2013年，世界天气研究计划(World Weather Research Program，WWRP)和世界气候研究计划(World Climate Research Program，WCRP)启动了次季节到季节预测项目[23]，本文对从S2S数据库中检索到的ECMWF的S2S回报数据进行订正.该预报由变分辨率集合预报系统(variable resolution ensemble prediction system，VarEPS)产生[24]，空间分辨率为1.5°×1.5°，提前期最长46 d，包含过去20年的回顾预报结果，降水预报形式为累计降水预报，共有11个集合成员.观测数据使用国家气象科学数据中心的中国全球大气再分析40年产品-逐6小时产品，该数据为空间分辨率0.5°×0.5°的每6 h累计降水.通过做差和求和，可以获得每日累计降水的预报结果和观测数据.通过双线性插值，将观测数据的分辨率调整到和预报数据一致的1.5°×1.5°，并取(21°-37.5°N，102°-124.5°E)范围作为输入数据和观测数据的范围.

3.2 评价指标

本文考虑使用CRPS、MAE(mean absolute error)和TS(threat score)作为评价指标，对订正后的预报结果从概率预报角度和确定性预报角度两方面进行评估.CRPS用于评估概率分布和真实降水之间的误差，为了保持和原始预报结果评估一致的评估模式，对概率预报的评估通过对分布采样获得的集合预报评估获得.确定性预报结果评估通过对采样结果的均值评估获得.使用MAE评估预报误差情况，TS评估预报落区的准确性.

MAE的计算公式如下：

(8)

其中，mui是i点概率分布采样结果的均值，yi是i点的标签值.

对于给定阈值τ，采样均值和观测值之间有如表1所示的混淆矩阵.

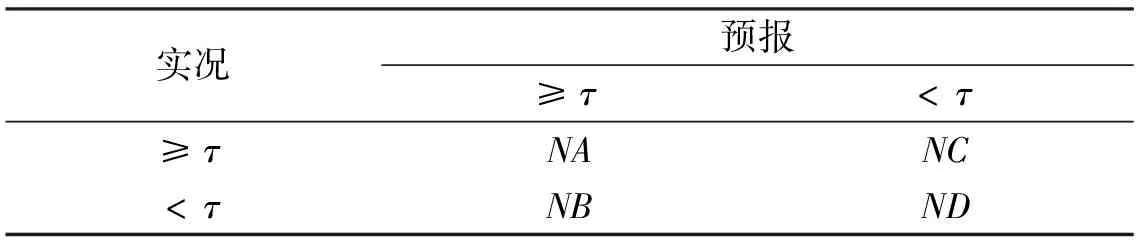
表1 混淆矩阵Tab.1 Contingency table

NA、NB、NC、ND分别表示满足条件的格点个数，TS评分的计算公式如公式(9)所示：

(9)

3.3 实验设置

本文使用2018版本的回报数据集，包含1998—2017年的回顾预报结果，使用1998—2011年的数据作为训练集，2012—2014的数据作为验证集，2015—2017年的数据作为测试集，参与对比的订正方法包括联合概率模型(joint probability model，JPM)[10]、U-Net和CPF-Net.

EC模式的确定性评估结果由EC模式的集合均值评估得到，各种订正方法都是对EC模式的集合均值进行订正，生成降水概率分布后采样得到集合预报，再对集合预报进行评估.JPM是短期降水预报订正最先进的方法，已经在澳大利亚气象局得到成功应用.U-Net和CPF-Net只在模型结构上有区别，其他细节完全一致，模型训练中的具体设置为：pow设为0.4，batch size设为256，使用Adam优化器，学习率为1e-4，最大训练轮次为120，随机种子设置为3 407，显卡使用Nvidia Tesla V100，每次训练取验证集上最佳的模型保存参数，然后在测试集上进行测试.

3.4 结果分析

3.4.1 整体结果分析

通过对2015—2017年的中国南部EC模式预报结果进行订正，结果如表2所示，所有结果均为评估结果均值，TS10和TS25分别表示10 mm和25 mm阈值下的TS测试结果.通过CPF-Net订正后，相对于EC模式预报结果，CRPS下降了14%，MAE下降了12%，TS10提高了48%，TS25提高了35%，CPF-Net在所有指标上均为最优，说明本文所提方法是一种效果显著的次季节降水预报订正方法.CPF-Net优于U-Net，也说明本文对U-Net的改进是有效的.

表2 次季节降水预报订正的对比实验结果Tab.2 Comparative experimental results of sub-seasonal precipitation forecast correction

3.4.2 逐日误差分析

通过对30个提前期的降水预报结果的CRPS分别进行评估，结果如图4所示.从整体看，所有订正方法和原始预报结果的CRPS都会随着提前期的增加不断增加，曲线之间的差距在开始时最大，后逐渐缩小，可能是因为随着提前期的增加，不确定性不断增加，订正可以消除的误差就相对较少.CPF-Net可以在全部30 d的提前期中保持最小平均误差，说明本文方法在误差消除上效果显著.U-Net可以在前几天优于JPM，随着提前期增加而慢慢接近JPM，这可能是因为不确定性增加，部分原有的误差模式不再可靠，而CPF-Net因为通道注意力机制可以针对不同提前期提取不同的特征，从而一直保持最小平均误差.

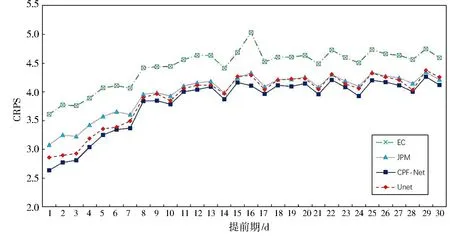
图4 逐日CRPS对比Fig.4 Day-by-day CRPS comparison

通过对30个提前期的降水预报结果的10 mm阈值TS评分分别进行评估，结果如图5所示.从整体看，所有订正方法和原始预报结果的TS评分都会随着提前期的增加不断减少，曲线之间的差距在开始时最小，之后逐渐扩大，这和CRPS的变化趋势有很大不同.这是因为降水事件发生频率较低，只要预报一个偏低的结果就可以保持一个相对不错的预报误差，而偏弱的降水预报就会导致TS评分的下降.CPF-Net可以在全部30 d的提前期中保持最高的TS评分，说明本文方法在预报的落区准确性上也效果显著.U-Net也可以全程优于JPM，这是因为通过损失函数加权，深度学习模型的预报偏好往强降水方向调整，所以TS评分优于JPM.

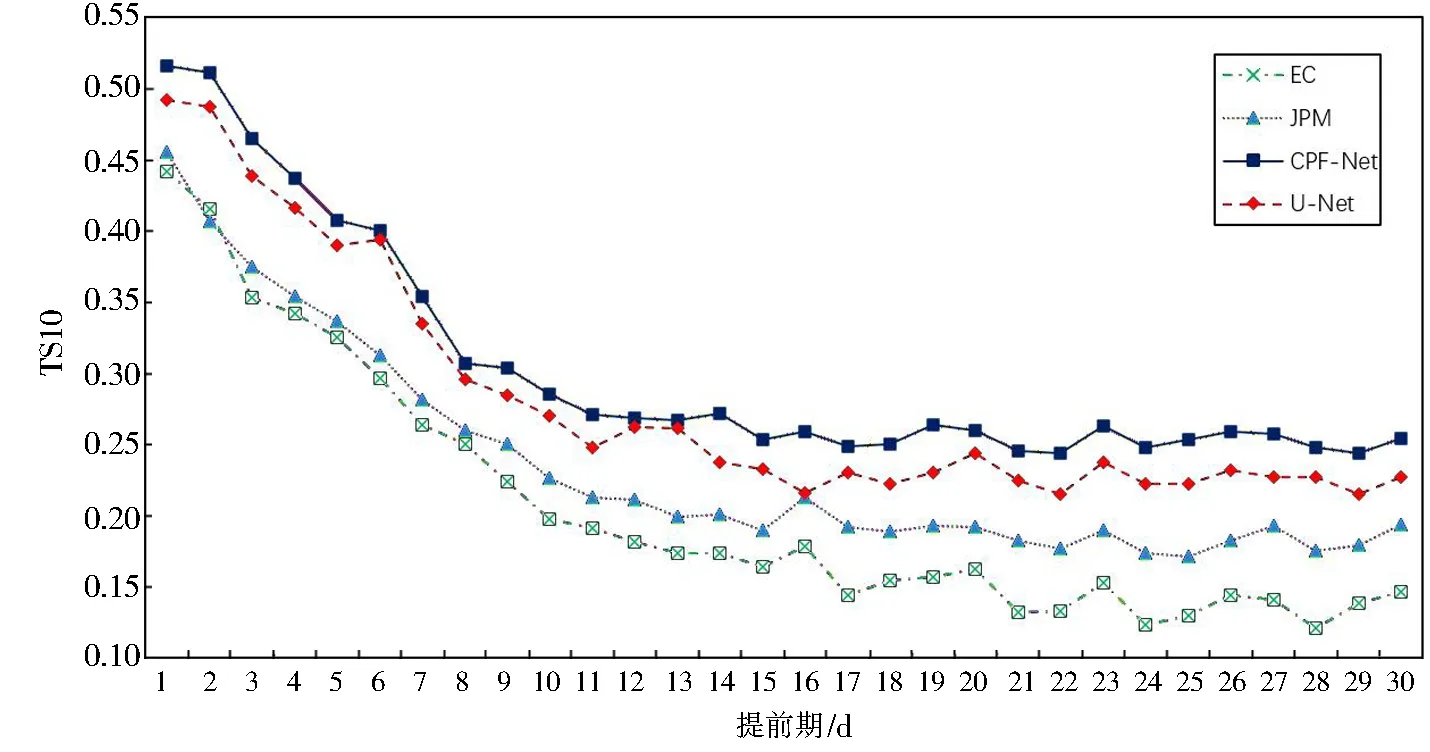
图5 10 mm阈值TS评分逐日对比Fig.5 Day-by-day comparison of TS scores at the 10 mm threshold

3.4.3 误差空间分布分析

通过对误差的空间分布进行分析，如图6(a)图所示的原始预报结果来看，误差整体从北到南，从西到东，呈增长趋势，越靠近赤道和海洋的地区，降水量越大，降水预报的误差也会越大.经过CPF-Net订正之后的结果如图6(b)图所示，相对原始预报，各个区域的误差都有所降低，这说明CPF-Net订正误差没有明显地区上的偏好，模型鲁棒性较强，这有利于将CPF-Net推广到其他地区做降水预报订正.

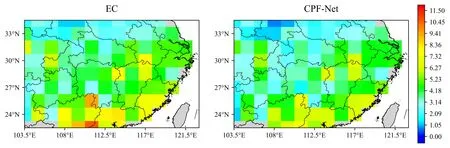
基于自然资源部标准地图服务系统审图号GS(2020)4619号标准地图制作，地图边界无修改图6 CRPS空间分布Fig.6 Spatial distribution of CRPS

3.5 消融实验

为了验证所提方法的有效性，对数据变换和损失函数加权进行消融实验，结果如表3所示.首先，从损失函数加权的有效性看，不管是进行数据变换的情况(表3第3行和第5行，此时，pow为0.4)还是未进行数据变换的情况(表3第2行和第4行，此时，pow为0.22)，做损失函数加权都能降低降水预报订正的CRPS；其次，从数据变换的有效性看，不管是有损失函数加权的情况(表3第2行和第5行)还是无损失函数加权的情况(表3第3行和第4行)，进行数据变换也都能降低降水预报订正的CRPS.以上对比说明，数据变换和损失函数加权均可以改善模型的订正效果.

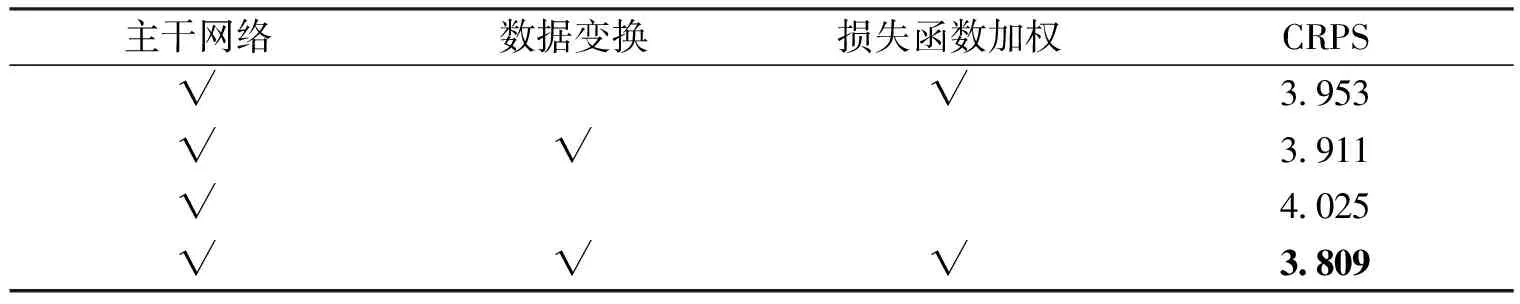
表3 数据变换和损失函数加权消融实验结果Tab.3 Experimental results of data transformation and loss function weighted ablation

由于pow这个超参是根据数据不平衡的程度灵活调整的，而数据变换前后数据不平衡性的程度不一致，所以，针对未做数据变换的原始数据仍然根据3.3节实验设置pow取0.4是不合理的，实验数据显示，针对未做数据变换的原始数据，调整pow为0.22，更为合理有效.

对模型结构改进的消融实验结果如表4所示.在有通道注意力机制的基础上(表4第2行和第4行)，加入残差块有效降低了CRPS；在有残差块的基础上(表4第3行和第4行)，加入通道注意力机制也同样降低了CRPS；表4第4行也达到了全文4种方法的最优CRPS值.从表4的消融实验结果可以看出，本文对模型的改进有效提升了模型性能.

表4 模型结构消融实验结果Tab.4 Results of model structure ablation experiments

4 总结

本文设计实现了一种基于深度学习的次季节降水预报订正方法，采用指数变换将降水数据变换到正态分布，而后使用正态分布对降水数据建模，使用CPF-Net对降水预报数据进行订正.实验表明，该方法在次季节降水预报订正上取得了较好的结果，可以显著降低预报误差，提高降水预报落区准确性，优于现有方法.但该方法还存在不足，虽然该方法使用了时间嵌入，但并没有对降水预报的时间相关性建模，在后续的工作中可以通过对时间相关性建模，探讨进一步提高订正效果的可能性.