一种无源被动式人体低重力模拟系统的力学性能仿真分析

宋天翔， 乔 兵

（南京航空航天大学航天学院， 南京 211106）

1 引言

随着载人航天任务的发展，航天员将面临登陆月球、火星任务，在此期间，航天员必然要完成各种复杂的舱外活动任务。 而在低重力环境下，人体的运动方式和运动感受与地面环境相比都会产生较大的变化［1］，长期处于微低重力环境还会对人体的各项生理功能产生负面影响［2］。 因此，在地面对航天员开展模拟失重环境下的训练就显得尤为重要。

自20 世纪60 年代以来，NASA 及各国航天机构开展了多种人体低重力模拟方法研究，包括抛物线飞行法［3］，中性浮力水池法［4］，悬挂法等。其中抛物线飞行法的模拟效果最为逼真，但该方法成本较高，并且一次抛物线飞行只能提供15 ～40 s 的微低重力环境［5－6］，同时，受限于狭小的机舱环境，航天员只能进行一些小幅度的运动训练。中性浮力水池法克服了模拟时间和空间的限制，在水池中可放置等比例的空间站模型辅助航天员训练，同时可以通过添加配重的方式来实现任意重力水平的模拟［6］，但水中的动态阻尼和粘滞效应会影响航天员的运动，且成本较高。 悬挂法是近年来研究较多的低重力模拟方法，NASA 研制出了部分重力模拟器（Partial Gravity Simulator，POGO）、主动响应重力卸载系统（Active Response Gravity Offload System，ARGOS）、零重力步行运动模拟器（Zero-Gravity Locomotion Simulator，ZLS）等悬挂式低重力模拟系统。 POGO 由垂直伺服系统、万向节系统、显示和控制系统组成［7］，其中垂直伺服系统通过气缸输送压缩气体，从而产生一个向上的托举力，同时可以在气浮导轨上任意移动，为航天员提供2 个平动自由度，万向节系统作为航天员和垂直伺服系统的连接结构，同时为航天员提供了3 个转动自由度。 基于部分重力模拟器的悬挂法克服了前2 种方法的缺点，但POGO的系统性能有限，无法较好地跟踪航天员的运动［8］。 为了弥补POGO 的不足，NASA 研制了ARGOS 系统［9］，其主动控制系统有较高的动态性能，能够跟踪人体的运动并实时调节吊索的拉力，低重力模拟精度有了很大提高。 但基于单点悬吊的重力平衡方式无法对人体四肢受到的重力载荷进行补偿。 NASA 和克利夫兰诊所联合研制的ZLS 系统解决了这一问题，该装置采用多根绳索将人体仰卧吊起，让航天员在垂直放置的跑步机上行走，从而研究零重力环境下的步态特征［10］。该方法的零重力模拟精度较高，但仅能提供2 个自由度，且运动舒适性较差。

为了解决上述方法存在的问题，研究人员将在医疗领域和工业机器人领域较广泛应用的减重外骨骼移植到了航天员失重模拟训练领域。Herder［11］研制的无能量系统以势能守恒原理为基础，将弹簧平行四边形机构作为基本组成单元，采用被动无源的方式平衡任意比例的人体重力［12］。 该装置可以同时应用到人体躯干和四肢，从而实现对人体各个部分的重力补偿。 此外，还为外骨骼系统设计了一套自适应调节机构，可以自动调节平衡弹簧的相关参数［13］。 陈卓鹏［14］、江一帆［15］也进行了相关研究，分别利用多刚体系统仿真软件和人体生物力学仿真软件对该机构进行了仿真分析，对比了月球环境步行和地球环境穿戴外骨骼步行2 种工况下的地面反作用力，肌肉力等数据。

对于上述被动式人体低重力模拟外骨骼，在实际应用时需要设计出满足弹性系数要求和最大伸长量要求的弹簧，这在弹簧设计时可能会存在困难。 针对这一问题，在设计人体低重力模拟外骨骼系统的基础上，本文采用了将弹簧和动滑轮相结合的方法，可以改变所需的弹簧弹性系数和最大伸长量。 此外，通过人体生物力学仿真软件从人体肌肉力、下肢关节驱动力矩和人体所受地反力的角度出发进行仿真分析，研究外骨骼重力和外骨骼关节处的摩擦力矩对低重力模拟效果的影响，并提出克服影响的解决方案。

2 模型设计

2.1 重力补偿原理

人体减重外骨骼系统的原理图及各项参数如图1 所示，由于上肢质量约占人体质量的5%［16］，为了简化系统的复杂度，此处暂时不考虑上肢的重力平衡，将上肢和躯干简化为一根连杆。

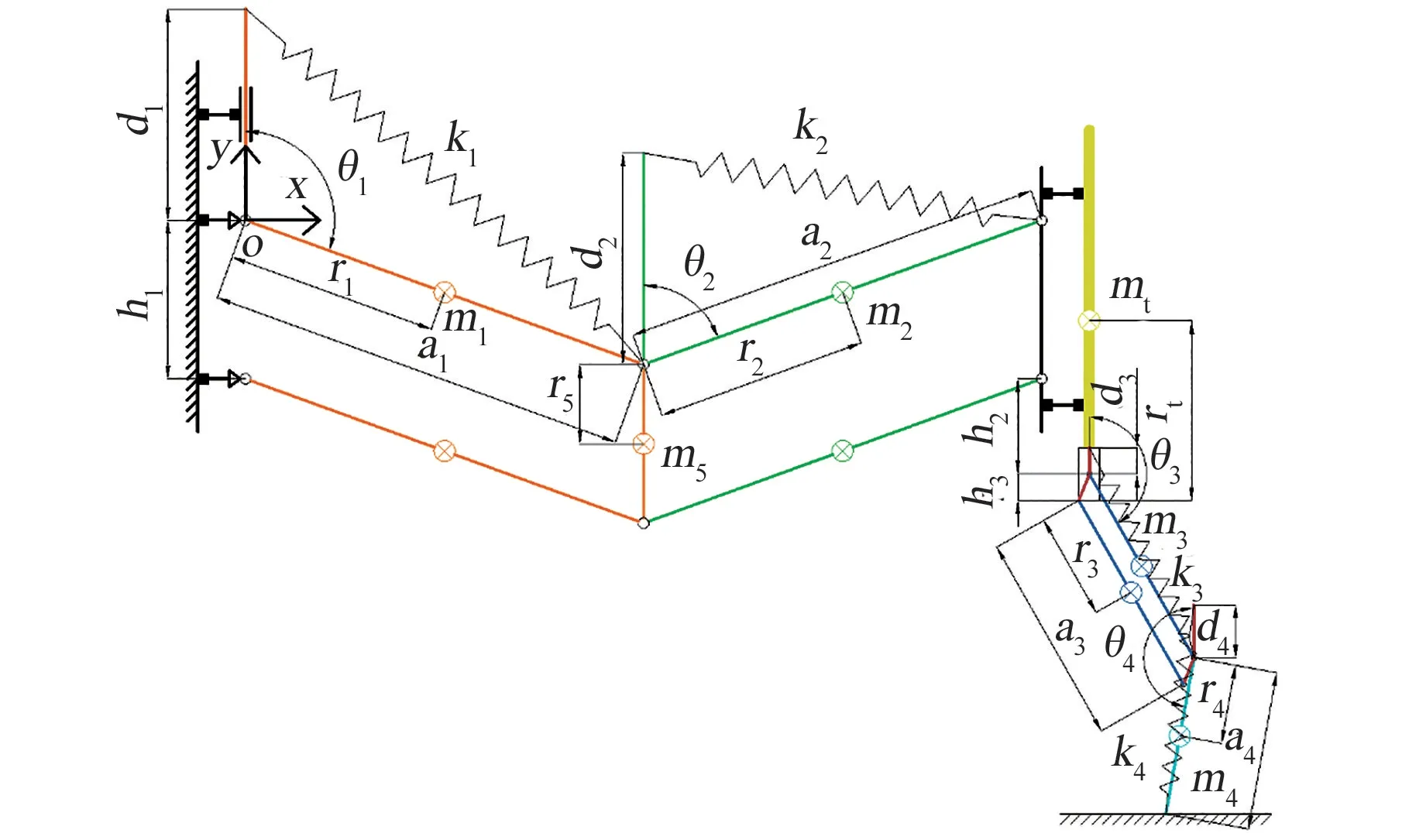
图1 人体减重外骨骼系统示意图Fig.1 Schematic diagram of the human body reduced-gravity exoskeleton system

假设图1 中各杆件均为匀质杆，杆件长度、质心位置和质量分别由li、ri和mi（i＝1…5）表示，ai和di分别表示弹簧位于连杆上的安装位置和在垂直端的安装位置，ki表示弹簧的弹性系数，hi表示杆件端点之间的垂向距离，θi表示各杆件和y方向的夹角，mt表示人体躯干的质量，rt表示躯干质心的位置，假设腿部的质心和杆3，4 的质心重合，质量分别为mlt和mls，忽略其他杆件的质量。 坐标原点O的位置如图中所示，z轴方向遵循右手定则。 整个人体减重外骨骼系统的总势能E包括弹性势能Ek和重力势能Eg，如式（1）所示。

假设弹簧的初始长度均为0［11］，则系统的弹性势能为式（2）。

以xoz平面为零重力势能参考平面，则系统的重力势能见式（3）～式（11），g为地球表面重力加速度。

若要实现人体的重力全部被平衡，则需满足E为常数，其中仅有θi会随着系统构型的变化而发生变化，因此需要满足θi的系数均恒为0，根据已知的各项几何参数可以得到ki，ai，di需要满足的条件如式（12）～（15）所示。

上述结论是在人体重力被完全平衡的条件下推导得出的，如果要平衡一定比例的人体重力，只需将mt、mlt和mls与平衡系数ρ相乘，例如模拟月球重力环境时ρ＝5／6， 模拟火星环境时ρ＝5／8。

2.2 弹簧安装方法

本文计算的弹性势能是基于假设弹簧零初始长度，即弹簧的伸长量等于弹簧的长度。 而在实际应用中，零初始长度弹簧是不存在的，为了保证弹簧的伸长量与图1 中弹簧长度相同，可以采用图2 中的弹簧安装方法，对于腿部弹簧，可以将其固定在腿部连杆上，通过定滑轮和牵引线将弹簧力引出。

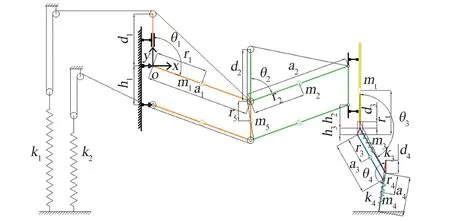
图2 弹簧安装方法Fig.2 Spring installation method

对于平衡躯干重力的2 根弹簧，即k1和k2，为了尽可能增大人体的运动范围，需要较大的弹簧伸长量，而在实际应用中，拉伸弹簧的最大伸长量不宜超过1.5 m，长细比不宜超过15，这就对人体的运动范围有了较大的限制。 因此，除了采用图2 中所示的定滑轮和牵引线来引出弹簧力外，还可以利用动滑轮来减小弹簧的最大伸长量。 如图中所示，采用动滑轮后，动滑轮移动的距离与理论上零初始弹簧的伸长量相同，而弹簧绕过动滑轮后的伸长量为相同条件下理论弹簧伸长量的1／2，同时弹簧的拉力变为理论弹簧的2 倍，即弹簧的弹性系数变为理论弹簧的4 倍。

2.3 低重力模拟系统的三维模型

在上述原理的基础上，设计了如图3 所示的人体低重力模拟系统，其中杆1，杆2 可较为准确地调节弹簧的安装位置，实现精确的低重力模拟。杆3～杆8 按照图3 中所示的连接关系互相铰接，形成了2 个平行四边形结构机构。 在杆3 和杆7上设计有固定牵引线的挂钩，定滑轮参照图2 的安装示意图所示，分别固定在杆1、杆2、杆5 以及框架上，牵引线可以按照图2 所示，绕过滑轮组与弹簧相连。 通过人体躯干部分的柔性背带和腰部的刚性腰带，可以将平衡力较为均匀地施加到人体，实现躯干减重的效果。 下肢重力平衡外骨骼与人体背后的支撑框架通过螺栓连接，在连杆9和连杆10 上分别设计了大腿固定板和小腿固定板，通过柔性绑带将腿部固定在下肢重力平衡外骨骼上，实现下肢减重的效果。

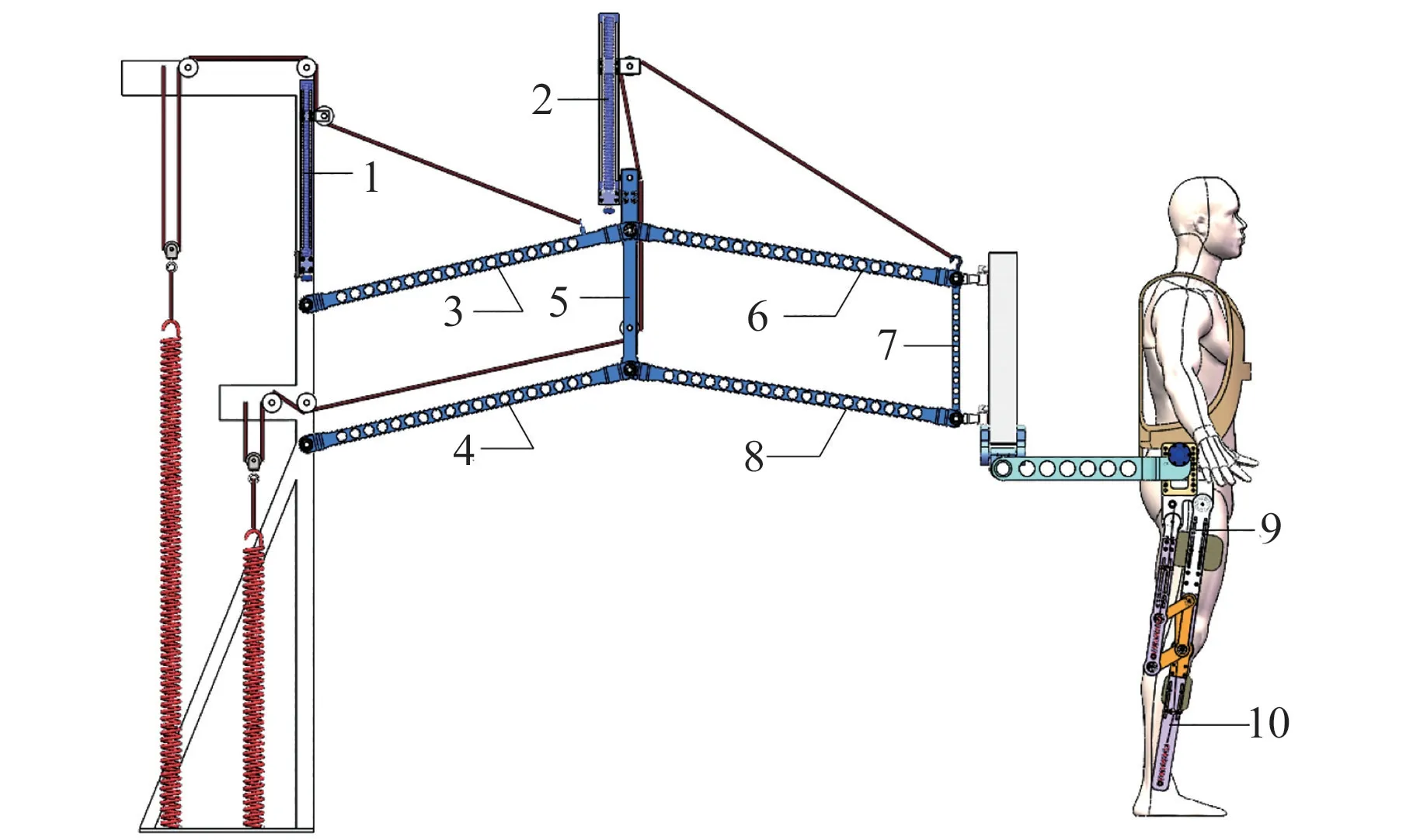
图3 人体低重力模拟系统的三维模型Fig.3 3D-model of human body reduced-gravity simulation system

3 仿真分析

为了验证人体减重外骨骼系统的效果，本文利用人体生物力学仿真软件Anybody Modeling System 7.4［17］进行仿真分析。 Anybody 基于人体解剖学数据，建立了完整的人体肌肉骨骼模型，可导入由动作捕捉系统生成的C3D（Coordinate 3D）数据或BVH（Biovision Hierarchical Data）数据来驱动人体进行运动，其中C3D 数据是通过记录标记点的位置变化生成的，BVH 数据是通过记录惯性测量数据生成的。 针对人体这一运动学超静定系统，通过Anybody 中针对超静定系统的多体运动学和多体动力学的相关算法［18］，可以计算出人体各个节段的运动学数据和各个关节的受力情况以及地面反作用力数据［19-20］；通过软件中的肌肉募集算法和肌肉覆盖算法［21］，可以计算出人体所有肌肉的肌肉力、肌肉活动度等数据［22］。 同时，Anybody 还与其他3 D 建模软件有良好的接口，可以将三维模型导入Anybody 与人体模型耦合，在外骨骼的早期开发过程中，可以帮助研究人员更方便地评估外骨骼的作用［23］。

仿真分析研究在月球环境和地球环境穿戴外骨骼两种情况下进行，共分为四部分：①搬运重物仿真实验，对比2 种工况下的地面反作用力、腿部关节驱动力矩和腿部肌肉力，其中地面反作用力可以衡量躯干重力平衡外骨骼的低重力模拟效果，腿部关节驱动力矩可以衡量下肢重力平衡外骨骼对下肢的低重力模拟效果，腿部肌肉力则可以从人体体感的角度衡量低重力模拟效果。 ②步行仿真实验，并改变外骨骼的质量，对比几种工况下的地面反作用力，以研究外骨骼质量对低重力模拟效果的影响。 ③步行仿真实验，并改变外骨骼关节的摩擦力矩，对比几种工况下的地面反作用力，以研究外骨骼关节摩擦力矩对低重力模拟效果的影响。 ④针对②、③仿真实验得出的结论，提出了适当增大弹簧弹性系数以减小低重力模拟误差的猜想，并针对该猜想进行相应的仿真实验，分析理论弹簧弹性系数外骨骼和增大弹簧弹性系数外骨骼的低重力模拟的性能差异。

3.1 搬运重物

针对较为常见的搬运重物，进行以下仿真实验：首先设定环境的重力加速度为1／6 G，采用Anybody 提供的BVH 数据驱动模型，整套动作为人体蹲下搬起12 kg 的重物后起立，并将重物抬至胸前再向前步行1 步，运动共耗时约2.5 s。 在完成第1 组仿真实验后将环境的重力加速度设置为1 G，在重物的质心处添加一个大小为98.1 N、方向竖直向上的力，以保证2 种环境下人体受到的由重力引起的载荷相同，将减重外骨骼与人体耦合后驱动人体执行相同的运动。 关节处的摩擦力采用库伦粘性摩擦模型［24］，摩擦力矩f可以表示为式（16）。

其中，θ·表示关节转动的角速度。 Anybody搬运重物仿真场景如图4 所示，在满足平行四边形结构提供的各项约束的前提下，省略了图3 中的1、2、6、7 号连杆，由于Anybody 中无法直接使用滑轮组、弹簧等机械元件，因此，直接将弹簧的拉力施加在连杆上，其他仿真参数如表1 所示。

表1 连杆和人体参数Table 1 Parameters of exoskeleton and human body

图4 Anybody 仿真场景（搬运重物）Fig.4 Anybody simulation scene （Handling heavy objects）

图5 为低重力模拟实验右足地反力数据，其中，GRFx为x轴地面反作用力（x-axis Ground Reaction Force），GRFy为y轴地面反作用力（y-axis Ground Reaction Force）， GRFz为z轴地面反作用力（z-axis Ground Reaction Force）；GRMx为x轴地面反作用力矩（x-axis Ground Reaction Moment）， GRMy为y轴地面反作用力力矩（y-axis Ground Reaction Moment）， GRMz为z轴地面反作用力矩（z-axis Ground Reaction Moment）。

图5 右足地反力对比Fig.5 Comparison of ground reaction force

由图5 结果可知，地面及月球重力情况下地反力数据变化的总体趋势相同，但GRFx和GRMy在运动初期和末期出现了一定程度的偏差，GRFz在运动初期和中期出现了一定程度的偏差，而GRFy、GRMx和GRMz在整个运动过程中吻合程度较高。 对于GRFx，可以观察到在运动初始时刻出现了方向相反的情况，这一误差可能由外骨骼的惯性引起，在穿戴外骨骼时对人体产生了“拖拽感”，因此地面反作用力的方向与理论情况相反。 考虑到y方向的地反力远大于x和z方向，x和z方向的地反力矩远大于y方向，可以认为GRFx，GRFz和GRMy的偏差对人体感知的影响较小，因此，从地反力角度可以认为躯干重力平衡外骨骼较好地模拟了低重力环境。

图6 展示了腿部关节驱动力矩。 由图6 结果可知，在2 种仿真环境下，y、z轴方向的踝关节驱动力矩在整个运动过程中的吻合程度较高，其余的4 种关节驱动力矩在运动前期产生了一定的偏差。 但考虑到腿部各关节的驱动力矩变化趋势总体相同，仍然可以认为在关节驱动力矩的角度下，下肢重力平衡外骨骼可较好模拟低重力环境。

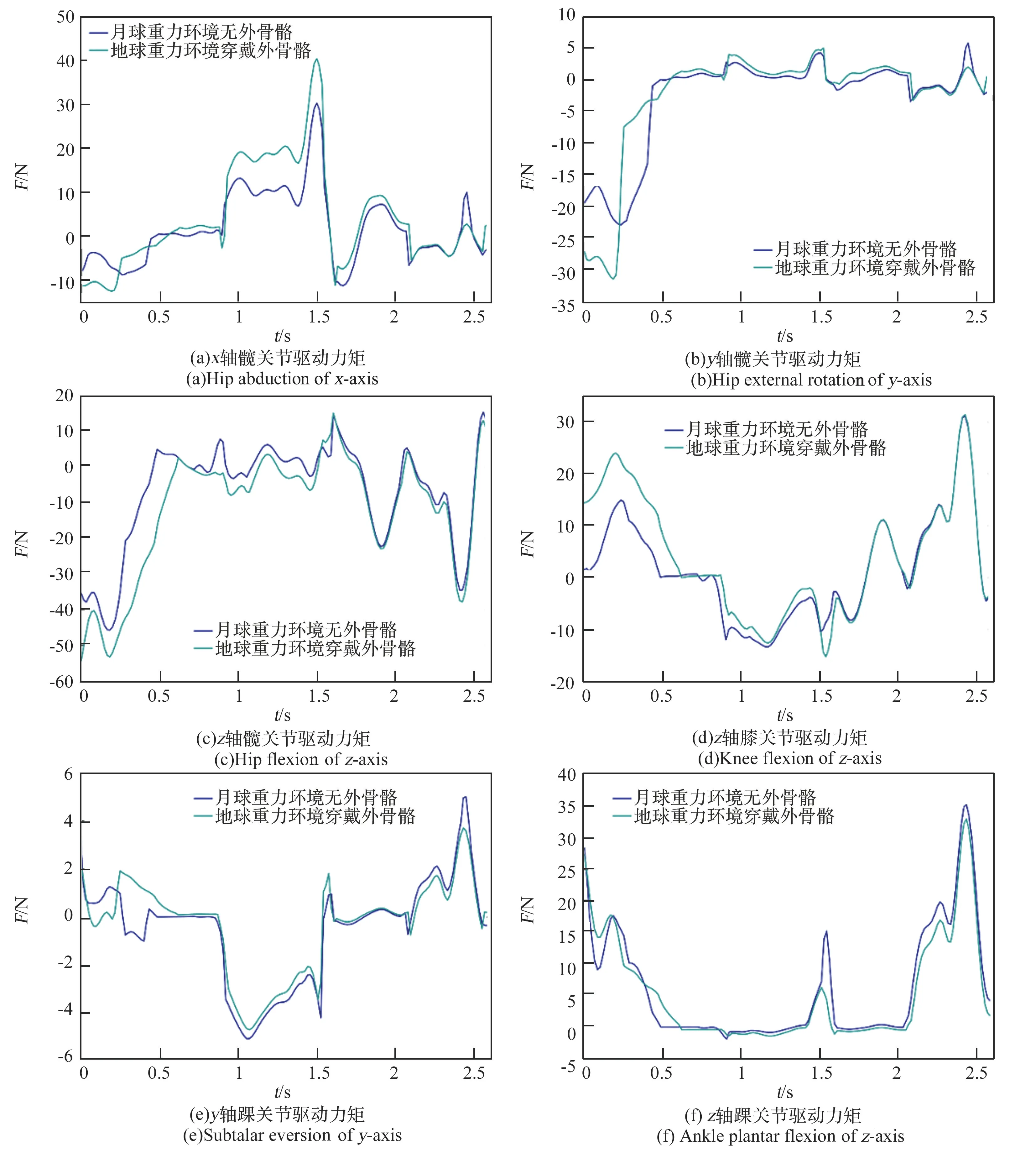
图6 腿部关节力矩对比Fig.6 Comparison of leg joint moment

考虑到大型肌肉肌力变化是衡量低重力模拟效果的主要因素，为了简化数据分析的复杂程度，图7 中仅展示了腿部大型肌肉的肌肉力数据。 由图7 可知，2 种情况下肌肉力数据的变化总体吻合，其中大收肌，腓肠肌，比目鱼肌的肌肉力在2 种情况下的吻合程度较高，股二头肌、股肌的肌肉力在实验初期产生了一定的偏差，在实验中期和后期的吻合程度较高，而半腱肌的肌肉力在实验前期及中期的吻合程度较低，且多个极值偏差较大。 产生偏差的原因可能是：①人体并不能简化为一个由匀质杆件组成的多刚体系统，由于人体内各种软组织的影响，身体各节段质心的相对位置可能会随着身体运动而产生变化；②人体的关节并非理想的旋转关节，部分关节处允许骨骼间产生较小的平移运动，例如膝关节处股骨和胫骨就会相对滑动。 上述情况会导致外骨骼对身体施加的平衡力难以满足理论要求。

3.2 外骨骼系统的质量对低重力模拟效果的影响

为了研究外骨骼系统质量对低重力模拟效果的影响，设计了以下4 组仿真实验：分别在月球环境下、使用减重外骨骼的地面环境下进行2 个步态周期的步行实验，人体模型采用Anybody 软件提供的C3D 数据驱动，仿真时间约1.8 s，多次调整用于躯干平衡的减重外骨骼的质量，即m1、m2分别设置为0 kg，2 kg，4 kg，忽略关节处的摩擦力矩，Anybody 中的仿真场景如图8 所示，得到了如图9 所示的地反力数据。 由于躯干重力平衡外骨骼主要影响的是地反力的变化，所以此处省略了对下肢肌肉力的研究。

图8 Anybody 仿真场景（步行）Fig.8 Anybody simulation scene （Walking）

由图9 结果可知，在外骨骼质量为零的理想情况下，除了GRFx与理论值产生了较小的偏差外，其他5 种地面反作用力都与理论值吻合，说明在步行情况下，减重外骨骼能较好实现低重力模拟。 随着外骨骼质量的逐渐增大，该系统的动态性能逐渐减弱，6 种地反力的实验值与理论值的偏差逐渐增大，外骨骼质量对其中GRMx和GRMy的影响尤为明显。

3.3 摩擦力矩对低重力模拟效果的影响

为了研究外骨骼系统关节处摩擦力矩对低重力模拟效果的影响，设计了3 组仿真实验：将躯干重力平衡外骨骼的杆件质量设置为2 kg，人体模型同样采用2 个步态周期内步行的C3D 数据来驱动。 为了简化仿真实验，关节处的摩擦力采用静态库仑摩擦模型［25］，为了放大摩擦力矩对仿真结果的影响，此处设计较大的摩擦力矩，分别设置为0 Nm，20 Nm，40 Nm，可以分别表示为式（17）～（19）。

得到的地反力数据如图10 所示。 根据图10的仿真结果，关节摩擦力矩主要会引起GRFx和GRMy产生变化，尤其是GRMy，除了会改变最大值外，还会引起GRMy在其峰值附近大幅波动，对于其他4 种地面反作用力，摩擦力矩的影响较小。同时，考虑到人体主要感知的2 种地反力为GRFy和GRMz，可以认为摩擦力矩对减重外骨骼系统产生的模拟误差较小。

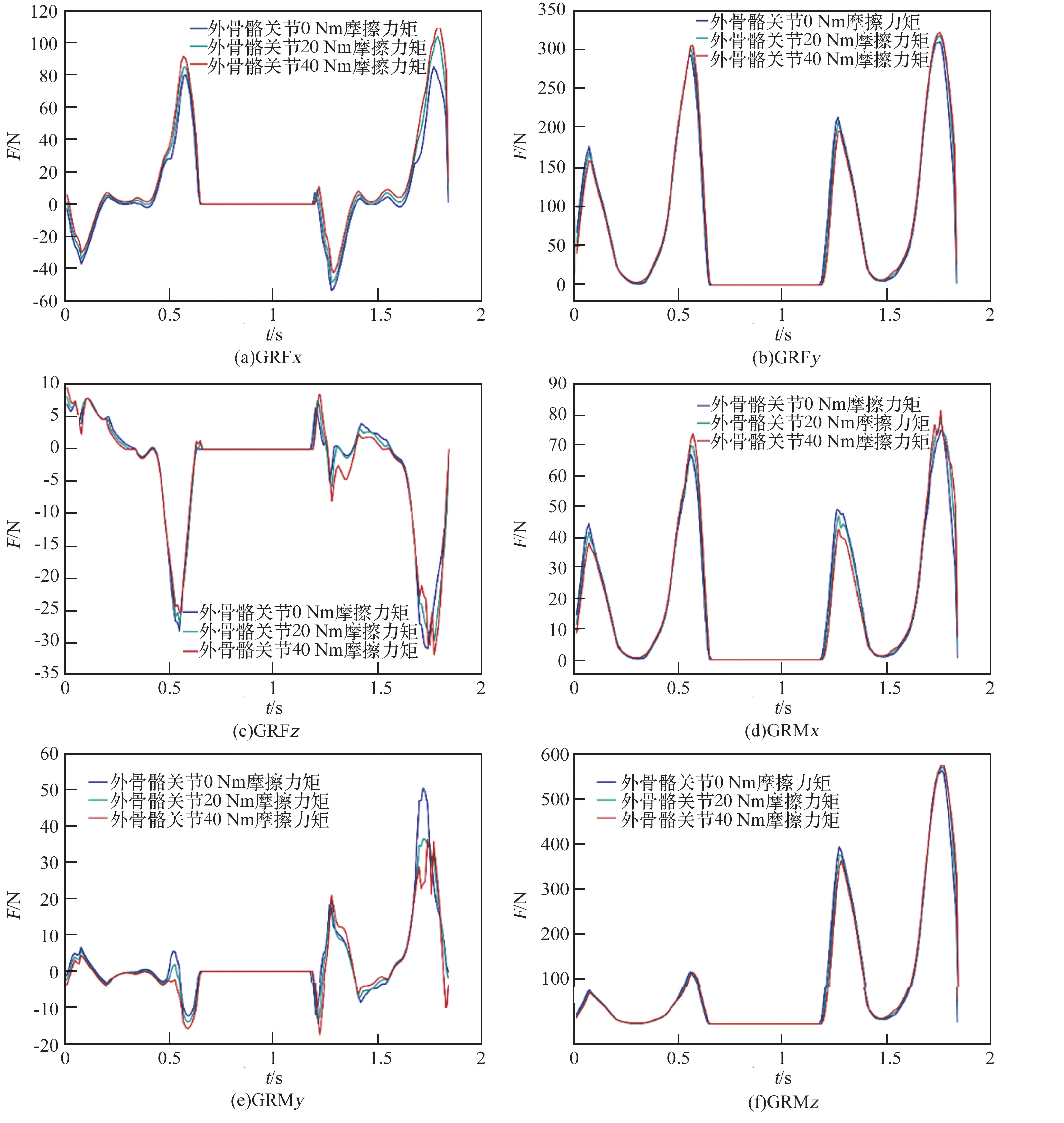
图10 关节摩擦力矩对地面反作用力的影响Fig.10 Influence of joint friction moment on ground reaction force

3.4 减小外骨骼质量对低重力模拟效果影响的方法

随着杆重的逐渐增大，外骨骼系统的动态性能会逐渐减弱，但与之相反，随着弹簧弹性系数的增加，该系统的动态性能会逐渐增强，因此，在保持其他参数不变的情况下，适当增加弹簧的弹性系数可以抵消掉由于外骨骼质量增大而引起的模拟误差。 由此设计以下3 组仿真实验： ①人体在月球环境步行； ②人体与外骨骼结合后在地面环境步行，将躯干重力平衡外骨骼的杆件质量设置为2 kg，关节处的摩擦力矩为恒定的20 Nm，弹簧弹性系数设置为理论值； ③在保持其他条件与第2 组相同的前提下，将弹簧弹性系数适当增大，仿真结果如图11 所示。

图11 弹簧弹性系数对地面反作用力的影响Fig.11 Influence of spring elasticity coefficient on ground reaction force

由图11 可知，人体感知最为明显的2 种地反力GRFy和GRMz几乎与理论值完全吻合，仅峰值对应的时间与理论值产生了微小的偏差，对于其他4 种地反力，增大弹簧弹性系数后对理论值的跟踪效果也优于理论弹簧弹性系数，说明该方法可以有效改进外骨骼系统的低重力模拟效果。

根据上述4 个方面仿真实验研究可知，本文设计的人体低重力模拟系统可以较为真实地模拟月球低重力环境，但由于系统设计是基于无能量系统中的静平衡机构设计的，且未使用主动控制系统，在面对复杂运动时，其较弱的动态性能会导致以下两点问题：①难以克服外骨骼质量和外骨骼关节摩擦力矩对系统的直接影响；②复杂的运动难以满足静平衡机构的要求。 但是，考虑到本系统是用于进行月面舱外活动训练而设计，在真实的月球环境中，人体更倾向于以更低的速度和加速度运动，而本文使用的模型驱动数据由Anybody 提供，数据是在地球环境下正常运动测得，人体的速度和加速度都较高，这也直接导致了较大的关节摩擦力矩。 因此，如果能更缓慢地完成2 个仿真实验中的动作，外骨骼的低重力模拟效果会更佳，外骨骼质量和关节摩擦力矩对系统的影响也会更小。

4 结论

1）本文设计了一种基于势能守恒原理，采用弹簧平行四边形机构的人体减重外骨骼系统，该系统结构简单，自由度多，可以模拟0 ～1 G 任意重力环境，能够实现局部重力和重力矩平衡，可实现地面模拟低重力步行和搬运重物的训练。

2）在实际情况中，考虑到所需弹簧的最大伸长量过大可能难以满足的问题，提出了一种借助动滑轮的弹簧安装方法，该方法可以在不影响人体运动范围的前提下有效减小弹簧的伸长量。

3） 利用人体生物力学仿真软件Anybody Modeling System 将外骨骼模型和人体耦合，验证了外骨骼系统在搬运重物和步行2 种工况下的低重力模拟效果，分析了外骨骼系统质量和关节摩擦力矩对模拟精度的影响。 仿真结果表明：外骨骼系统质量对模拟精度的影响较大，而关节摩擦力矩的影响相对较小，因此，在进行外骨骼设计时可采用轻质材料（如碳纤维）并进行结构优化，尽可能减小外骨骼质量；还可以通过适当增加弹簧的弹性系数以提高系统的动态性能，达到减小低重力模拟误差的目的。