飞机紧固孔周疲劳裂纹扩展微观分析
王锡芝,张剑伟,刘贞言,帅馨禹
(1.辽宁石油化工大学机械工程学院,辽宁抚顺 110179;2.沈阳航空航天大学安全工程学院,辽宁沈阳1 101361;3.沈阳城市学院智能与工程学院,辽宁沈阳 110112)
目前,将飞机的一些构件连接起来采用的主要连接方法仍是机械连接。一架飞机上少的时候会有几十万铆钉和螺栓,多的时候会有几百万个铆钉和螺栓。紧固件连接孔的位置是飞机连接结构易发生疲劳破坏的位置之一[1],已经发现的裂纹可能导致飞机翼下纵梁断裂,裂纹的扩展会使大翼下纵梁缘条产生裂纹。如果纵梁裂纹未被发现,将导致飞机燃油泄漏,增加火警风险或发生更多不安全事件,最终严重影响飞机整体结构的完整性和飞行安全,导致空中事故和人身安全[2]。因此,对飞机紧固件连接孔周疲劳裂纹起裂和扩展过程的研究意义重大。
疲劳裂纹扩展可以分为两个阶段。第一阶段是滑移,接着产生微裂纹,最后微裂纹连接形成宏观微裂纹的过程;第二阶段是宏观裂纹逐渐扩展直至断裂的过程。通常,疲劳裂纹扩展第一阶段的裂纹是沿着最大切应力方向向内扩展。而其中多数微裂纹为不扩展裂纹,只有个别微裂纹可延伸几十微米(约2~3 个晶深[3])。因此看不到或者是很少能看到塑性变形的特征,这一阶段所占的面积也很小。人类用肉眼不易看到,所以对疲劳裂纹扩展第一阶段的研究远远少于第二阶段。固体材料的损伤和破坏是指它在使役过程中,由于内部大量微损伤微裂纹或孔洞的萌生、扩展和连接,导致材料宏观力学性能的劣化乃至最终失效它是当前力学界与工程界均十分关注的一个焦点,也是固体力学的基本问题之一[4]。因此,疲劳裂纹扩展的微观分析方法显得尤为重要,与此同时也是寻求控制疲劳裂纹起裂和扩展的必经之路,具有重要的科学意义和实用价值。
1 分析方法
机械连接是一架飞机连接其结构壁板的典型连接方式,紧固件孔是典型的应力集中部位和疲劳源。裂纹常产生于连接件搭接内表面紧固孔边缘、沉头螺栓头下锪窝棱线等疲劳薄弱部位[5]。
文章涉及一种应用于飞机紧固件连接孔周疲劳裂纹扩展的微观分析方法,主要步骤如下:
(1)根据飞机连接结构,推导出紧固孔周围最大应力σmax,并将最大应力转化成裂纹萌生和扩展所需的局部力ƒg,应力分布情况示意图如图1。
(2)设置工况,建立紧固孔周围最大应力处裂纹起裂的微观模型,对微裂纹的疲劳扩展进行数值模拟分析。
(3)分析预制裂纹长度、所处环境温度、疲劳应力载荷幅值、不同纳米材料和不同裂纹扩展晶向对裂纹萌生和扩展行为的影响。
疲劳品质指数为:
式中:SF是疲劳品质指数;α是紧固件孔条件系数;β是孔的填充系数;σ1是由紧固件载荷ΔP传递引起的局部应力;σ2是由旁路载荷P引起的局部应力;σ是结构中的参考应力;ΔP是通过紧固件传递的载荷;P是旁路载荷;D是紧固件直径;t是搭接板厚度;W是搭接板宽度;Kth是挤压应力集中系数,Kth=σmax/(ΔP/Dt);Ktg是应力集中系数,Ktg=σmax/σ;θ是挤压分布系数。
紧固孔周围的最大应力为:
裂纹萌生所需的局部力(名义应力)为:
式中:A是将最大应力转化成名义应力的参考系数。工作应力低于屈服强度,连接结构表面会在循环应力和应变的双重作用下产生微观裂纹,然后微观裂纹逐渐扩大达到临界数值,就会导致连接结构的破坏,这种破坏称为疲劳破坏。导致疲劳破坏的交变应力就称为疲劳应力。fg是随时间周而复始变化的交变应力,示意图如图2。

图2 疲劳应力示意图
EAM势函数:
式中:Etot代表体系中全部质点的总能量;Ei代表质点i的内能;ρi代表全部其他质点作用在质点i上的质点云密度;Fi(ρi)代表质点i嵌入到质点云密度ρi中的嵌入能;rij是质点i和质点j之间的间隔距离;fj(rij)是距离质点i为rij的质点j对质点i产生的作用。
应力计算上采用维里(Virial)统计平均应力[6]。就是把模型系统所受到的力平均分配到模型系统中的每一个质点上。具体公式如下:
2 模型建立
2.1 基本算例
运用分子动力学软件LAMMPS 对飞机紧固件连接孔周疲劳裂纹扩展进行微观尺度数值模拟分析。预制裂纹长度为10 nm;温度首先控制在300 K;疲劳应力载荷的幅值设置成3/fs。计算过程中模型的尺寸为长60 nm,宽20 nm,厚4 nm;边界条件设置为SSP;采用NVT 系综;势函数选取EAM 势;积分时间步长为1 fs。SSP 边界条件:长和宽方向是自由边界,厚度方向是周期性边界。NVT 系综:质点个数保持不变,系统真实体积相同,环境温度控制恒定。
疲劳应力载荷循环62 500 次、75 000 次、87 500次、100 000次时,分别记录裂纹扩展行为时刻图如图3。发现随着循环次数的增加,裂纹逐渐变长。从局部放大图中可以看到,裂纹扩展的微观过程是裂尖两个原子受力分开的过程。裂尖两个原子分开后形成新的裂尖,新裂尖处又有两个新的原子受力分开,以此类推裂纹逐渐向前推移扩展。通常,宏观力学认为距离裂纹尖端越近应力越大,无限接近裂纹尖端应力将趋近于无穷大,这是不符合物理规律的。更有,裂纹尖端应力到底达到多少时裂纹起裂也是宏观力学无法触及的“黑匣子”。然而从微观角度来分析,裂纹尖端是由原子分布形成的,裂纹的扩展过程是克服裂纹尖端两个原子相互作用力的过程,而这个力的大小约为4.5 GPa 左右。也就是说裂纹尖端应力值达到4.5 GPa 左右时,裂尖处两个原子被分开裂纹向前扩展。裂纹的相互作用长期被认为具有取向敏感性,但裂纹相互作用的原子尺度机制以及有效裂纹尖端抗阻如何随不同边界条件而变化尚不清楚[7]。

图3 裂纹长度与疲劳应力循环次数关系
从局部放大图中也可以看到,当疲劳应力载荷开始作用不久后,在各个晶粒的内部就会出现滑移线,滑移线的位置分布不均匀,仅出现在局部的区域。随着疲劳载荷对晶粒的作用,晶粒内部原位置滑移线的滑移量逐渐增加,而新滑移线也往往在原有滑移线位置的附近出现,这两部分滑移线进而组成滑移带[8]。而在滑移带与滑移带之间的表面上却看不到滑移线。随着疲劳作用的进行,滑移带的范围也逐渐扩大,裂纹也越来越深,进而在表面上出现“侵入沟”和“挤出带”,出现的“侵入沟”就是疲劳裂纹的源头,也就是疲劳源。
2.2 预制裂纹长度的影响
采用控制变量分析方法。环境温度恒定在300 K。疲劳应力载荷的幅值设置成3/fs。预制裂纹长度分别取10 nm、20 nm 和30 nm 进行数值模拟分析,结果如图4。
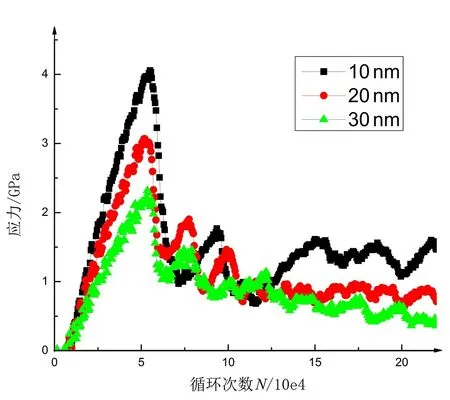
图4 应力和循环次数之间关系曲线(S-N曲线)
从图中可以看出,随着疲劳应力载荷循环次数的增多,裂纹尖端应力值逐渐增大。将局部屈服应力σmax分别代入紧固孔周裂纹萌生扩展所需的局部力公式fg=Aσmax可 得:fg(10 nm)=4.06 A,fg(20 nm)=3.07 A,fg(30 nm)=2.32 A,得出紧固孔周预制微裂纹越长裂纹萌生扩展所需的局部应力越小。除此之外,应力集中导致裂纹尖端由弹性阶段进入塑性变形阶段,裂尖钝化后向前扩展。预制裂纹越短,裂纹尖端应力值上升越快。当疲劳应力载荷循环次数达到一定值后,裂纹尖端应力值达到屈服强度后开始急剧下降,此时裂尖突破塑性阶段的束缚裂纹发生扩展。预制裂纹越短的模型屈服强度越大,越不容易发生断裂破坏。无论预制裂纹长度如何,裂纹起裂时外界疲劳应力载荷循环次数相同,都在50 000 次左右。说明裂纹在疲劳应力作用下起裂与初始裂纹长度无关。
2.3 环境温度的影响
采用控制变量分析方法。预制裂纹长度为10 nm。疲劳应力载荷的幅值设置成3/fs。环境温度分别取100 K、200 K 和300 K 进行数值模拟分析,结果如图5。

图5 应力和循环次数之间关系曲线(S-N曲线)
从图中可以看出,随着疲劳应力载荷循环次数的增多,裂纹尖端应力值逐渐增大。将局部屈服应力σmax分别代入紧固孔周裂纹萌生扩展所需的局部力公式fg=Aσmax可得:fg(100 K)=4.44 A,fg(200 K)=4.32 A,fg(300 K)=4.06 A,得出紧固孔所处环境温度越高周围裂纹萌生扩展所需的局部应力越小。除此之外,所处环境温度越高,裂纹尖端应力值上升速率越为缓慢。当疲劳应力载荷循环次数达到一定值后,裂纹尖端应力值达到屈服强度后开始下降,裂纹发生扩展。所处环境温度越低的模型屈服强度越大,越不容易发生断裂破坏。这是由于温度可以改变材料尤其是金属材料的延展性,温度越高模型延展性越好质地越柔软越容易变形破坏。所处环境温度越低的模型,裂纹起裂时外界疲劳应力载荷循环次数越少,预制裂纹越容易发生扩展。这是因为温度越低裂尖越容易进入塑性阶段,低温下裂纹越容易发生脆裂。
2.4 材料的影响
采用控制变量分析方法。预制裂纹长度为10 nm。疲劳应力载荷的幅值设置成3/fs。环境温度300 K。材料分别用铝(Al)、铜(Cu)和金(Au)进行数值模拟分析,结果如图6。
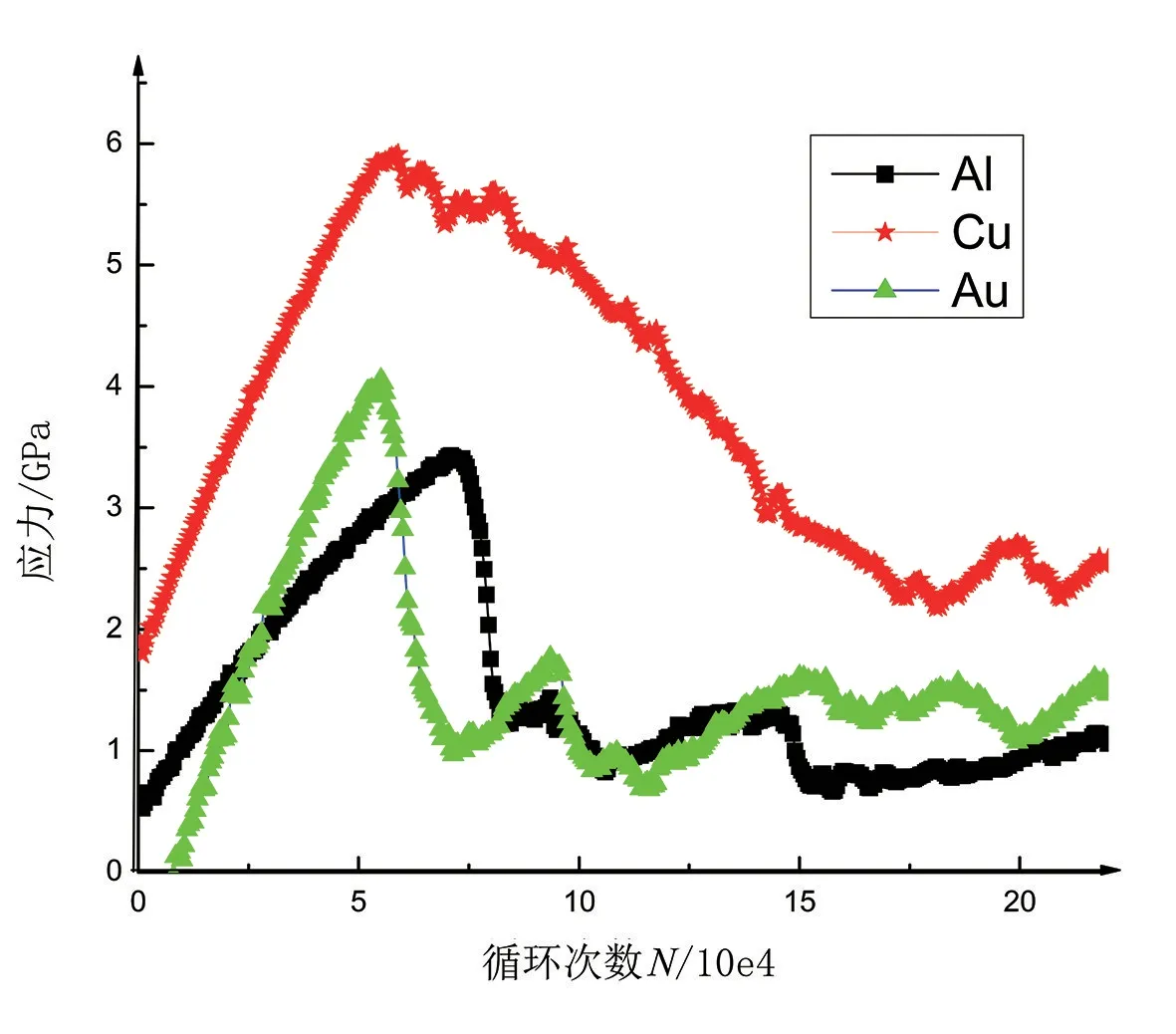
图6 应力和循环次数之间关系曲线(S-N曲线)
从图中可以看出,随着疲劳应力载荷循环次数的增多,裂纹尖端应力值逐渐增大,且铝纳米板应力值增大的速率相对其他两种材料更为缓慢。将局部屈服应力σmax分别代入紧固孔周裂纹萌生扩展所需的局部力公式fg=Aσmax可得:
fg(Al)=3.42 A,fg(Cu)=5.91A,fg(Au)=3.99 A,得出Cu纳米板紧固孔周围裂纹萌生扩展所需的局部应力最大,金纳米板次之,铝纳米板紧固孔周围裂纹萌生扩展所需的局部应力最小。除此之外,铝纳米板裂纹尖端应力值上升速率比铜和金要缓慢。当疲劳应力载荷循环次数达到一定值后,裂纹尖端应力值达到屈服强度后开始下降,裂纹发生扩展。铝纳米板模型屈服强度最小,且裂纹起裂得最晚。这是由于铝基金属材料质地较为柔软,延展性比其他两种纳米材料要好。
2.5 晶向的影响
采用控制变量分析方法。温度为300 K 的情况下,预制裂纹长度为10 nm,疲劳应力载荷的幅值设置成3/fs,材料选择铝(Al)基材料,将裂纹的扩展方向上的晶向分别设置为[1 0 0]、[0 1 0]和[0 0 1]进行数值模拟分析,结果如图7。
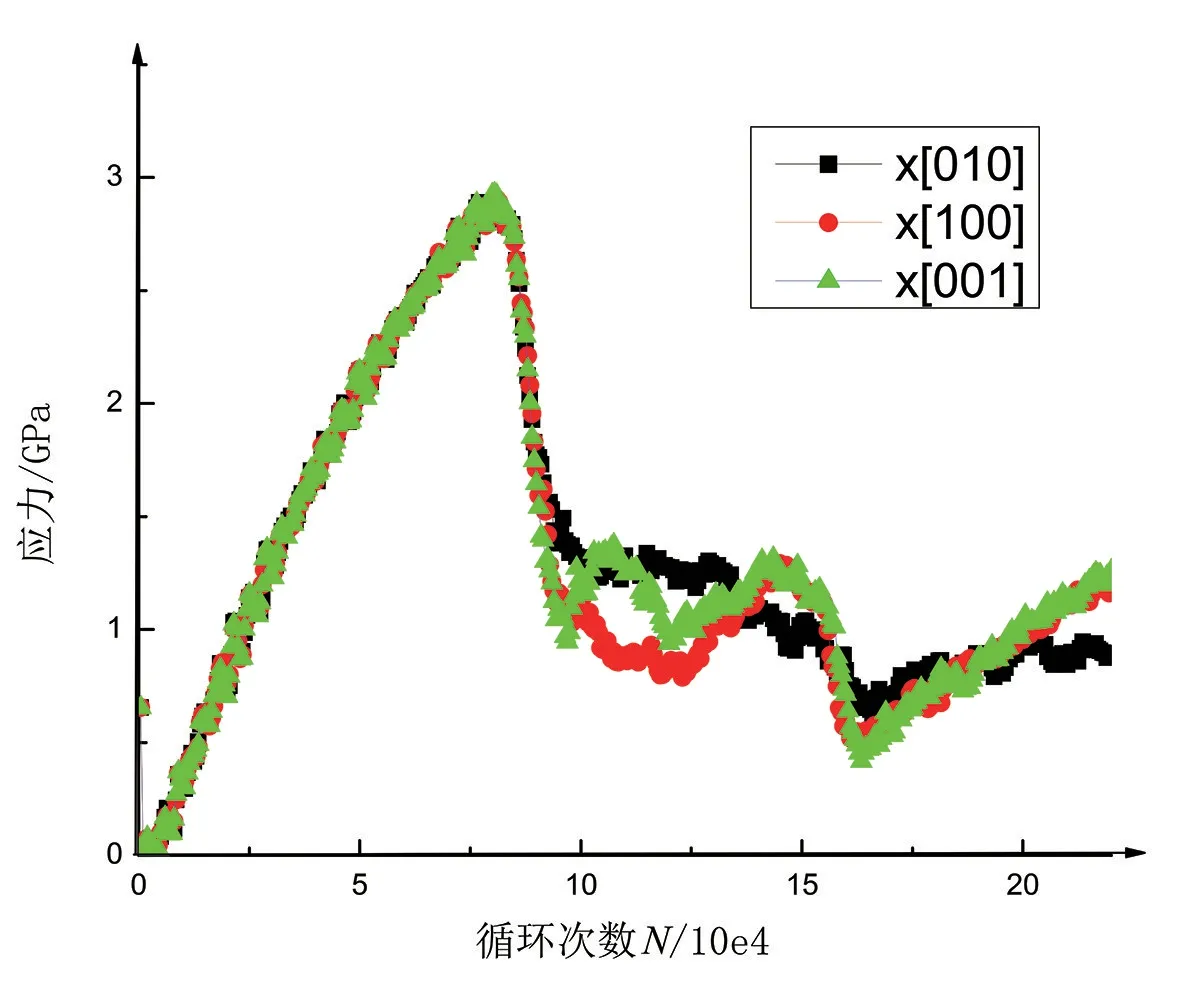
图7 应力和循环次数之间关系曲线(S-N曲线)
由于裂纹上扩展的晶向具有方向性,沿晶格方向晶体的性质不同,分别从裂纹晶向[1 0 0]、[0 1 0]和[0 0 1]角度看,在一定的范围内不同晶向的裂纹扩展应力是呈统一上升趋势。但是在峰值之后随着循环载荷次数增多出现明显差异。因此可以得出裂纹扩展方向上的晶向不同,对裂纹扩展有一定程度的影响。
将局部屈服应力σmax分别代入紧固孔周裂纹萌生扩展所需的局部力公式fg=Aσmax可知:fg([100])=2.89 A,fg([010])=2.89 A,fg([001])=2.89 A,得出沿裂纹扩展方向晶向不同时紧固孔周围裂纹萌生扩展所需的局部应力是相同的。
疲劳应力载荷循环100 000 次以后,发现裂纹尖端应力值有所差异。[0 1 0]晶向裂纹尖端应力值最大,[0 0 1]晶向次之,[1 0 0]晶向裂纹尖端应力值最小。这是因为[1 0 0]晶向与裂纹扩展方向是相互平行的,所以裂纹容易扩展,且裂纹尖端应力值也就最小。而[0 1 0]和[0 0 1]晶向与裂纹扩展方向是相互垂直的,所以会阻碍裂纹沿x方向扩展。由于模型z方向厚度4 nm 远小于y方向宽度20 nm,即使二者晶向都与裂纹扩展方向相互垂直,但是y方向晶格数要比z方向上的多,所以[0 1 0]晶向裂纹尖端应力值要大于[0 0 1]晶向裂纹尖端应力值。综上,这种形状纳米薄板,且裂纹扩展方向沿x方向,选取[0 1 0]晶向铝基纳米材料相比之下比较好。
3 结语
揭示了飞机紧固孔周疲劳微裂纹起裂和扩展的行为过程,同时也丰富了人类对纳米级尺寸裂纹的认识与理解。对于飞机紧固构件来说,多次、反复使用是在所难免的。在低于紧固孔周材料屈服极限的反复疲劳应力作用下,裂纹会萌生并慢慢扩展,从而使裂纹逐渐扩大到临界尺寸[9],最后导致脆断。裂纹的扩展过程用微观分析方法解释是克服裂纹尖端两个原子相互作用力的过程。分析了预制裂纹长度、温度、疲劳应力幅值、不同纳米板材料和不同裂纹扩展晶向对裂纹起裂和扩展行为的影响,得到如下结论:
(1)预制裂纹越长的模型屈服强度越小,越容易断裂破坏。受到同样的疲劳应力载荷作用时裂纹起裂的早晚与预制裂纹长度无关。
(2)所处环境温度越高的模型屈服强度越小,越容易断裂破坏。受同样的疲劳应力载荷作用时,所处环境温度越高的裂纹起裂越晚。
(3)不同材料Cu、Al 和Au,纳米板裂纹扩展,发现Al的弹性模量最小,模型的屈服强度也最小,受到同样的疲劳应力载荷作用时裂纹起裂的最晚。
(4)沿裂纹扩展方向晶向不同,疲劳应力载荷循环100000 次以后,[0 1 0]晶向裂纹尖端应力值最大,对裂纹扩展阻碍程度最深。[0 0 1]晶向次之,[1 0 0]晶向最差。

