强非局域介质中余弦高斯光束的动力学行为

臧 峰，刘利锋

（1.山西大同大学固体物理研究所，山西大同 037009；2.山西大同大学微结构电磁功能材料山西省重点实验室，山西大同 037009）

近年来，非局域介质因其在全光开关以及全光信号处理[1]等领域具有广阔的应用前景而受到科研人员青睐。其中，光束在非局域非线性介质（Nonlocal nonlinear medium）中的传输问题更是引起了人们极大的兴趣。事实上，非局域介质是指光场在某一位置所诱导的折射率变化不仅与该点的光场有关，同时还与一定范围内的其他点的光场有关。根据介质响应函数的宽度与入射光束宽度的大小关系，可以将其分为局域、弱非局域、一般非局域和强非局域[2]。光束在非局域介质中的传输可以由非局域非线性薛定谔方程[3]来描述，尤其是在强非局域介质中（响应函数的宽度远大于入射光束宽度），非局域非线性薛定谔方程可以简化为著名的Snyder-Mitchell线性模型[3-4]。基于这一线性模型，一些特殊光束的传输特性被广泛地研究，例如椭圆-高斯光束[5]、拉盖尔-高斯光束[6]、旋转抛物线柱面光束[7]、艾利-高斯光束[8]、厄米-正弦-高斯（HSG）光束[9-12]等。

另一方面，余弦高斯（Cos-Gaussian）光束由于其特殊的属性同样也引起了科研人员的关注[13-14]，相关研究结果已被报道。2011 年，Chen 等研究了正余弦高斯光束在Kerr 介质中的传输特性[15-16]，研究结果表明当初始功率较低时，正弦-高斯光束在克尔介质中传输时将演化为双曲正弦-高斯型光束。文献[17]数值研究了余弦高斯光束在偏置光折变晶体中的传输和相互作用。结果表明，当自聚焦非线性效应较小时，单个余弦高斯光束可以演化为Y 型呼吸孤子。文献[18]利用解析方法研究了余弦高斯光束在强非局域非线性介质中的传输特性，并且得到了光束宽度变化的解析结果和光束宽度不变时所需的临界功率。

文章基于强非局域非线性薛定谔方程的简化形式，采用分步傅里叶算法，对余弦高斯光束在强非局域非线性介质中的动力学演化特性进行了数值研究，讨论了不同参数对余弦高斯光束传输动力学的影响。

1 理论模型

光束在强非局域非线性介质中沿z轴传输的动力学过程可以由非局域非线性薛定谔方程来描述[8]，即

其中：k=ωn00是介质的线性折射率）是波数；ψ(x,z)是光束的复振幅包络；x和z分别是光场的横向和传播方向；η是与介质有关的常数；R(x)是非局域介质的响应函数。对于强非局域非线性介质，即当响应函数的特征宽度比光束的特征宽度大得多时，通过引进无量纲变换，方程（1）可以化简为如下形式[8,20]：

方程（2）是具有抛物势阱的线性薛定谔方程，也就是量子力学中的一维谐振子方程。无量纲后横向和传播方向分别用ρ0和来度量，ρ0是任意长度。α代表抛物势阱深度，在光学中对应介质的折射率变化率。

2 数值结果

在数值模拟过程中，选择的初始余弦高斯光束具有如下的函数形式：

其中：A是光束的振幅；b是余弦函数的调制参数。以方程（3）作为初始入射光束，通过数值模拟，可以得到余弦高斯光束的动力学演化行为。从公式（2）和公式（3）中能够看出，参数α和b是影响其动力学特性的主要因素。因此将分别讨论抛物势阱深度α和余弦调制参数b对余弦高斯光束动力学行为的影响。

2.1 调制参数对余弦高斯光束传输特性的影响

图1 显示的是在参量b不同的情况下余弦高斯光束的演化情况（图a、c、b 分别为1.5、2.5、3.5），其中α=0.6。从图中可以看出余弦高斯光束在强非局域介质中会呈现出周期性呼吸行为，且随着b的增大，光束呼吸的波腹也会逐渐变宽，当b增大到一定程度时，在波腹处光束完全分裂成两束。事实上，余弦高斯光束可以看成两个具有相反拖尾的类艾利光的叠加，且b越大它们的拖尾越就越明显，这样它们的自加速效应越强，分裂现象越明显。

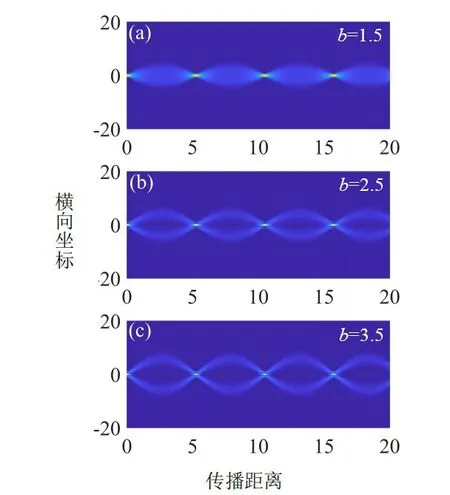
图1 余弦高斯光束在不同参数b下的演化行为

为了进一步研究这种分裂行为，图2（a）给出的是与图对应的三种情况下的波腹处的光场强度分布。从图中可以看出，随着调制参数b的增大，x=0 处的强度会变小，当b增加到一定程度，x=0 处的强度几乎为0，这意味着光束已经完全分裂成两束。图2（b）显示的是图1 三种情况下轴x=0 上的光场强度随z的演化情况，从图可以清楚地看到光场表现出周期性的演化行为，光场结构经过一定的传输距离得到恢复。进一步的研究发现轴上光场强度最小值Imin出现在波腹处，且b越大光场强度最小值Imin越小，当b增加到一定程度，Imin几乎等于0，这与图2（a）得到的数值结果是吻合的。图2（c）是在α=0.3、0.6、0.9 时，轴上光强最小值Imin对参量b的依赖关系。从图中可以看出，随着b的增大Imin逐渐减小，当b≥3.5，Imin几乎为0。

图2 调制参数对余弦高斯光束传输特性的影响

2.2 势阱深度对余弦高斯光束传输特性的影响

这一节，研究参数α对光束传输动力学的影响。当b=2.5时，数值模拟了不同α下余弦高斯光束的动力学行为，相应的结果显示在图3中。在图3中，从上向下α的取值分别为0.3、0.6、0.9。从图可以明显地看到α越大传输周期越小，同时光束在横向上的范围也会越小。

图3 余弦高斯光束在不同参数α下的演化行为

为了进一步研究这种现象，数值给出了传输周期对抛物势阱深度α的依赖的关系，如图4，从图可以看出，周期随α的增加而减少，这与文献[18]中的解析结果T=2π是完全一致的。α越大意味着折射率的变化率就越大，这样对光的约束也就越强，因此光束在横向上被局限在一个较小的范围内。

图4 余弦高斯光束的演化周期对势阱深度α的依赖关系

3 结语

采用数值方法研究了余弦高斯光束在强非局域非线性介质中的动力学行为，讨论了抛物势阱深度和余弦调制参数对余弦高斯光束动力学行为的影响。研究结果表明：光束传输周期只与抛物势阱深度有关，势阱深度越大光束传输周期越小，光束振荡振幅越小。此外，余弦调制参数对光束演化行为的影响也被详细地考虑，结果显示：余弦调制参数会影响光束的分裂行为，调制参数越大在波腹处光束的分裂行为就越显著。这些研究结果有可能在余弦高斯光束的操控方面有着潜在的应用价值。