基于等几何分析的板壳结构形状-拓扑协同优化
郝 鹏,张越一,金灵智,冯少军,王 博
(大连理工大学工程力学系工业装备结构分析优化与CAE软件全国重点实验室,大连 116023)
0 引言
板壳结构在航空航天领域已经获得了广泛关注,其轻质化是提升运载火箭结构系数的重要途径[1]。在以往研究中,结构轻量化设计一直是一个热门主题,国内外学者进行了大量探索,主要采用有限元方法作为分析手段。然而,对于复杂板壳结构,采用传统有限元方法进行优化是低效的。Hughes等[2]提出了一种基于样条函数的等几何分析(IGA)方法,采用非均匀有理B样条(NURBS)精确灵活描述几何模型,实现与分析模型之间的无缝集成,分析效率更高。
结构优化是轻量化设计的主要技术手段,包括尺寸优化、形状优化和拓扑优化。本文主要探究形状优化与拓扑优化。在形状优化早期,选取有限元离散化边界节点的坐标作为设计变量[3]。但这种方法面临着一个难题,即不可避免地会出现边界不规则与非光滑现象。等几何方法具有高精度、精确几何控制、计算机辅助设计(CAD)与计算机辅助工程(CAE)无缝结合等优势。因此,相关学者将其应用于结构形状优化。关键步骤是利用控制点坐标作为设计变量直接描述形状,平滑边界的同时也使分析模型准确代表了结构的几何模型。Qian[4]提出了一种计算NURBS控制点位置和权重的全解析灵敏度分析方法,将控制点和权系数同时作为设计变量,大幅提升了设计空间。面向加筋薄壁结构的形状优化设计,Hao等[5]提出了基于等几何的形状优化与筋条布局同步优化框架,该方法具有一定的准确性、灵活性与稳健性。
拓扑优化方法能够在规定的设计区域内使定量材料达到最佳分布形式。但目前大多数拓扑优化方法中的数值分析主要采用有限元法,具有以下限制[6]:1)有限元网格无法准确描述结构几何,降低了数值精度。2)低阶(C0)连续性影响了优化结果的准确性。3)高质量有限元网格实现起来较为困难。为了突破上述局限性,Feng等[7]提出了一种有效的B样条参数化方法,用于壳体结构的筋条布局优化,采用有限元法和固壳耦合法进行分析,得到了清晰布局。随着等几何的发展,有学者提出了基于IGA的拓扑优化方法,Kang等[8]通过使用NURBS修剪曲线代表孔的方式进行壳结构的等几何拓扑优化工作,得到了光滑连续的材料布局。Gupta等[9]提出了一种新的使用PHT(Polynomial splines over Hierarchical T-meshes)样条的自适应等几何拓扑优化方法。如上所述,等几何思想已经在很大程度上用于结构优化。
由以往研究可知,形状优化无法改变拓扑构型,而拓扑优化的初始设计域固定,因此两种方法均存在一定的限制。为此,相关学者相继提出了不同的形状与拓扑组合优化形式。Ansola等[10]提出了一种形状与拓扑的集成优化方法,执行了连续的两步程序,形状与拓扑交替进行。Hassani等[11]基于有限元分析对壳体结构同时进行形状和拓扑优化。Zhu等[12]提出了一种耦合形状与拓扑优化(CSTO)技术用于支撑结构的设计。Jiang等[13]提出了一种基于移动变形构件(MMC)方法的显示形状与拓扑同时优化方法,最终优化结果可实现与CAD系统的转化。上述研究结果表明,采用一些组合优化形式更能使结构获得良好性能。
基于以上工作,本文提出了一种基于等几何分析的形状与拓扑协同优化方法。采用NURBS精确描述几何模型,提供高平滑度并实现对形状的灵活控制。将控制点坐标定义为形状变量,控制点密度定义为拓扑变量。由于结构形状的改变,需要更加精细的网格进行描述,因此通过等几何分析可避免有限元中重新划分网格的复杂过程。同时,采用3场SIMP方法(固体各向同性材料密度惩罚模型)获取清晰边界并消除中间密度。与经典拓扑优化结果对比,新方法不仅保证了计算效率与计算精度,而且得到了更高性能的优化结构。
1 板壳结构的等几何分析
1.1 NURBS的基本原理
本节主要介绍以B样条为基础的NURBS曲面[14]。基于B样条基函数可以得到NURBS基函数,NURBS基函数的权重和非均匀节点矢量使其在描述几何形状时更加灵活。对于NURBS曲面,双变量的分段有理基函数可定义为
(1)
其中,i=1,2,…,n+p+1;j=1,2,…,m+q+1,n和m分别是ξ方向与η方向上基函数的个数,p和q分别为ξ方向与η方向上基函数的阶次,Ni,p(ξ)和Nj,q(η)分别是p阶和q阶的单变量B样条基函数,wi,j表示Ni,p(ξ)Nj,q(η)的相关权重。则NURBS曲面可定义为
(2)
式中,Pi,j是控制点。
1.2 基于NURBS的退化壳单元
在以往的工作中,已经将基于NURBS的退化壳单元用于复杂壳体的等几何静力与屈曲分析[15]。在退化壳单元中,任一点的总体坐标可近似地表示为结点坐标的插值形式,即
(3)
其中,t为壳体厚度,v3i为壳体局部法向矢量,ζ为高度方向上参数坐标。
根据壳体理论的基本假设,变形前中面的法线变形后仍保持为直线,且忽略其长度的变化,因此壳体内任一点的位移可由中面对应点沿总体坐标x,y,z方向的3个位移分量(ui,vi,wi)及该对应点的法线绕与它相垂直的两个正交矢量的转动(θxi,θyi)所确定。基于二阶基函数的退化壳单元局部坐标和位移如图1所示。

图1 基于二阶基函数退化壳单元局部坐标系及控制变量
通过精确的方向矢量,位移矢量可表示为
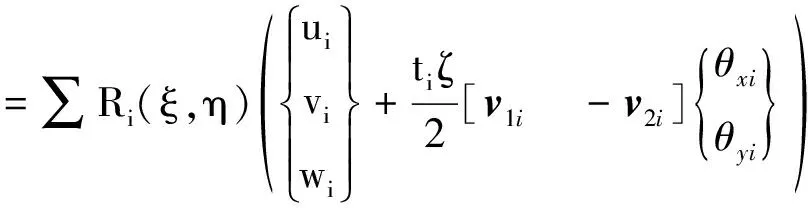
(4)


ifi×v3i=0,

(5)
弹性矩阵的表达式如下
(6)
该矩阵取决于材料的杨氏模量E和泊松比ν,k是考虑剪应力沿厚度方向不均匀分布的影响而引入的修正系数。整理后可得到退化壳的总体刚度阵
K=∑Ke
=∑(∑BTDB|J1||J2|w1iw2iw3i)
(7)
其中,Β为局部坐标系下的应力应变矩阵,w1i,w2i,w3i分别表示3个方向上的权系数,J1,J2为雅可比矩阵,J1用于物理空间与参数空间的转换,J2用于参数空间与母空间之间的转换。J1和J2分别表示如下
(8)
(9)
有关退化壳单元刚度阵与雅可比矩阵的详细推导过程可参考文献[16]。
2 形状-拓扑协同优化
2.1 等几何形状优化
体积约束下,最小应变能为目标函数的形状优化问题可描述为
(10)
C为目标函数,U为结构总位移,F为载荷,V0为结构初始体积,f为规定体积约束。设计变量为控制点坐标xs,xsmin与xsmax分别为自定义的设计变量坐标变化上下限,用于规定设计域的变化边界,因此,采用移动渐近线(MMA)算法更新形状变量。
2.1.1 解析灵敏度
目标函数对设计变量的偏导数为
(11)
(12)
其中,由于矩阵B在不同条件下是不断变化的,因此,∂B/∂xs的计算是一个繁琐的过程。另外,可采用半解析法或有限差分法近似计算形状变量灵敏度,但解析法能得到更准确的灵敏度信息,关于解析解的推导过程可参考文献[16]。
2.1.2 多水平模型
采用多水平模型说明等几何形状优化下的灵敏度传递问题,如图2所示,包括初始模型、分析模型与设计模型。初始模型具有较少控制点,通过细化增加控制点得到设计模型,进一步细化得到分析模型满足数值分析精度。设计变量定义在设计模型中,但目标函数由分析模型求解。在IGA的h细化过程中,原控制点被消除并被新控制点取代,保持结构形状不变的同时确保分析准确性。因此,可以实现灵敏度从设计模型到分析模型之间的传递。NURBS曲面的h细化过程可参考文献[16]。
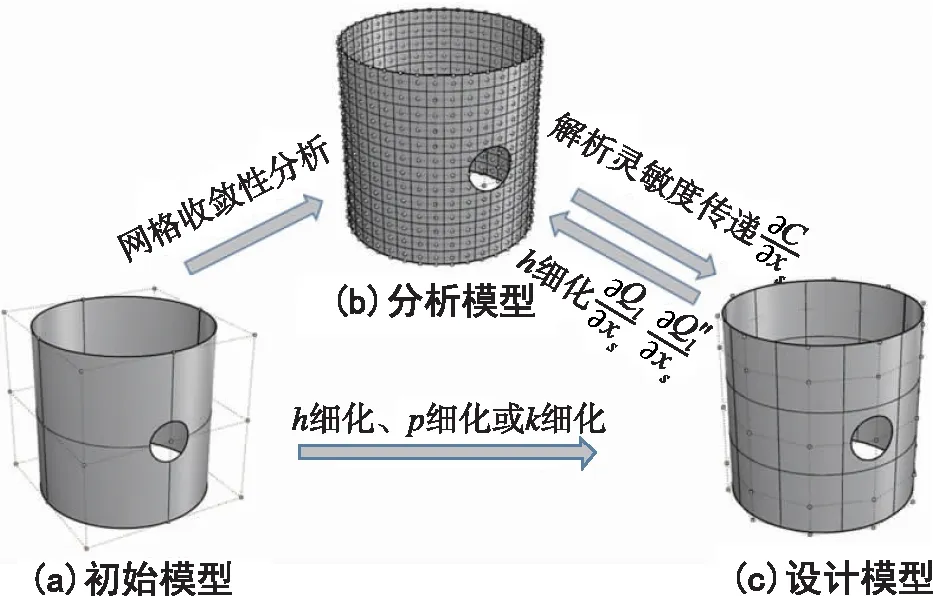
图2 多水平模型的网格与控制点
(13)

wQi=αiwi+(1-αi)wi-1
(14)
新控制点的物理坐标可表示为
(15)
在h细化的过程中,只有控制点发生变化。因此,相对于目标函数的灵敏度传递被转化为控制点坐标的灵敏度传递。相对于设计变量的新控制点灵敏度表示为
(16)
2.2 等几何拓扑优化
在等几何拓扑优化过程中,为获得更加清晰且光滑的边界,消除中间密度,采用3场SIMP方法,即在过滤密度的基础上,通过投影方式实现过滤密度的清晰化。体积约束下,最小应变能为目标函数的拓扑优化问题可描述为
(17)
设计变量为控制点密度xc,构造增广拉格朗日函数,柔顺度可表示为
C=FTU+λT(KU-F)
(18)
(19)
定义伴随方程FT+λTK=0,载荷与结构无关时∂F/∂xc=0,同时考虑刚度阵的对称性Kλ=-F。由KU=F可知λ=-U,故灵敏度可表示为
(20)

密度过滤的表达式如下
(21)
其中,
Hei=max{rmin-Δ(e,i),0}
(22)
式中,rmin为过滤半径,Δ(e,i)为两控制点之间的距离。
为了消除过滤带来的灰度单元,之后通过投影实现清晰的优化构型。本文采用正切型Heavi-side函数,表达式如下
(23)
其中,η为投影阈值,β控制着函数在η附近的陡峭程度。
采用优化准则法(OC)进行迭代求解,设计变量的迭代更新表达式为
(24)
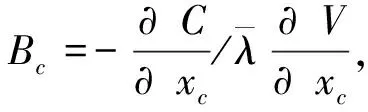
2.3 等几何形状-拓扑协同优化
基于等几何分析的形状-拓扑协同优化流程图如图3所示。采用一种先等几何形状优化,后等几何拓扑优化的协同优化方法,对求得的最佳结构形状进行拓扑优化,求解新结构在体积约束下的最小应变能。
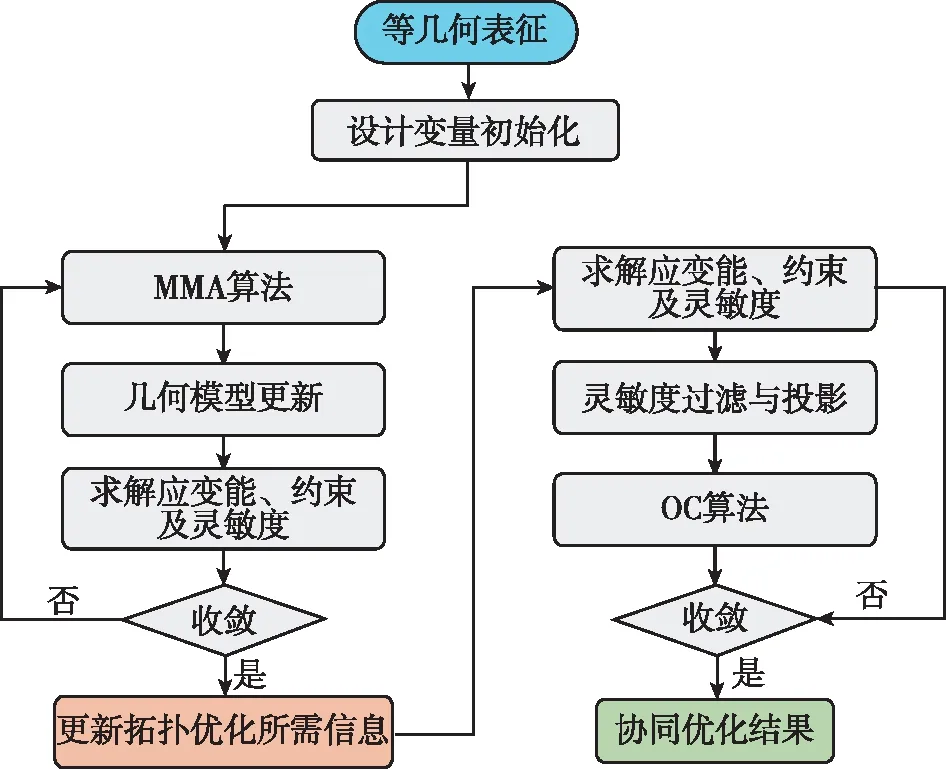
图3 基于等几何分析的形状-拓扑协同优化流程图
3 算例
在本章中,通过3个数值实例验证所提出的方法。第1个是拓扑优化中的常用测试算例,即平面MBB梁问题。第2和第3个例子是具有不同类型载荷条件的曲面问题,以此来验证所提出框架对复杂曲面的适用性。所有NURBS模型均采用3阶,模型参数均是量纲为1,材料属性如下:弹性模量E=1,泊松比ν=0.3。壳体结构的厚度为1,过滤半径为2,Heaviside函数中β=2,η=0.5。目标函数为最小应变能,约束函数为使目标体积小于或等于初始体积与体分比的乘积。为了验证形状-拓扑协同优化框架在结构轻量化设计方面的高效性,3个算例均与经典等几何拓扑优化结果进行对比。
3.1 MBB梁
首先考虑MBB梁,边界与载荷条件如图4所示,边长分别为600与100,模型的初始体积为60 000。形状优化方面:考虑对称性,选取初始模型的1/2为设计域,取其左侧4个控制点的y向坐标作为形状变量,其中上边界的1,2号控制点的y向坐标改变量上下限是[-50,50](初始y向坐标为50,则坐标范围是[0,100]);下边界3,4号控制点的y向坐标改变量的范围是[-230,-50](初始y向坐标为-50,则坐标范围是[-100,-280]);形状优化体积约束为整体体积的2.0倍。拓扑优化方面:分析模型的控制点为100×25,每个控制点的密度设置为设计变量,拓扑优化体积约束为整体体积的0.25倍。因此,形状-拓扑协同优化的总体约束为初始体积的0.5倍。作为对比算例,在经典等几何拓扑优化方法中,保持与形状-拓扑协同优化相同的体积约束,总体积的约束值是初始体积的一半。

图4 集中载荷作用下的MBB梁
所提方法与经典等几何拓扑优化方法下参数域内的密度分布函数(Density Distribution Function,DDF)图在图5中给出,可初步观察到结构构型的变化,所提方法下的结构杆件个数明显减少。迭代曲线及优化过程中的一些中间设计如图6所示。从形状优化的迭代进程中可知,结构设计域向下演化,整体框架逐渐加宽,收敛速度快,稳定性强。结构的体积与应变能均在前4步内急剧变化,在第19步达到最佳形状。在拓扑优化结果中,应变能在前10步内明显减少,之后细微调整直至收敛,最终为桁架状结构。对于类似结构,Rong等[17]使用不同方法获得的优化结果如图7所示,该方法通过增减子域的方式来重塑设计域,之后在自适应设计域中执行拓扑优化。由图7可知,所提方法得到了相似的构型。两种方法下使用的单元类型不一致,因此无法直接比较目标函数值。但值得注意的是,Rong等方法下的设计变量个数为98,优化周期较长,而提出方法的设计变量个数为4,优化迭代次数较少,只采用了极少的形状变量,且收敛速度快,稳定性强。
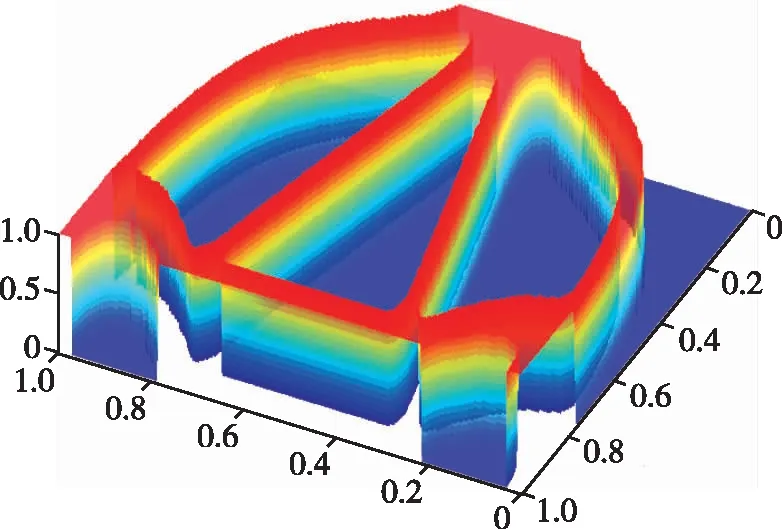
(a)等几何形状-拓扑协同优化方法

(a)形状优化结果C=0.112 8

(a)MBB梁载荷与边界条件
经典等几何拓扑优化方法下的迭代曲线与中间设计如图8所示。与图6协同优化方法下的优化结果对比发现,在体积基本相同的条件下,应变能相对减小了45.89%,得到了更高性能的结构,验证了该方法的高效性。为了更清晰地展示结构形状变化,所提方法下优化前后的控制点y向坐标见表1。可明显地观察到控制点变化的对称性,下边界大幅度下移,结构整体加宽。

表1 MBB梁优化前后控制点坐标

图8 MBB梁的经典等几何拓扑优化结果C=1.110 6
3.2 集中载荷下的自由曲面
中心点受集中载荷的自由曲面问题如图9所示,其投影边长为200,初始体积为40 720,4个端点固支。形状优化方面:根据对称性,选取初始模型的1/8作为设计域,取3个坐标方向为形状变量,1号控制点的z向坐标,改变量范围是[-50,50],2号控制点的z向坐标与x向坐标(根据对称性,正交方向上的形状变量则为y向坐标),改变量范围均是[-30,30],形状优化体积约束为整体体积的1倍。拓扑优化方面:分析模型的控制点为60×60,每个控制点的密度设置为设计变量,拓扑优化体积约束为整体体积的3/10。因此,形状-拓扑协同优化的总体约束为初始体积的3/10。作为对比算例,在经典等几何拓扑优化方法中,保持与形状-拓扑协同优化相同的体积约束,总体积的约束值是初始体积的3/10。

图9 集中载荷作用下的自由曲面
如图10所示,分别得到两种优化方法下参数域内的DDF图,可见二者结构形状差别不大。形状-拓扑协同优化结果如图11所示,形状优化方面:中心控制点z向坐标增大,结构具有更大翘曲度,体分比存在振荡,但并未达到目标约束,这说明获得最佳结构形状时所需材料并不多。拓扑优化方面:应变能与体分比均迅速达到稳定状态,结构中心开孔数量逐渐增多且清晰。

(a)等几何形状-拓扑协同优化方法
经典等几何拓扑优化结果如图12所示,对比两组优化结果发现,形状-拓扑协同优化方法的最终优化结构具有更大的弯曲程度。虽然形状优化中结构体积并未达到目标约束,但应变能相对减少了71.80%,节省材料的同时结构性能进一步提高。形状-拓扑协同优化方法下优化前后的控制点坐标见表2。由表2可知,中心控制点z向坐标已达到最大值,四边中点坐标向内向上移动,结构翘曲度增大。

表2 自由曲面优化前后控制点坐标

图12 自由曲面的经典等几何拓扑优化结果C=769.908 4
3.3 均布载荷下的半圆柱壳
最后考虑半圆柱壳问题,模型尺寸与边界条件在图13中给出,其直径为6,高度为12,初始体积为113,方向向下的均布载荷作用在高度方向边界上,4个端点固支。形状优化方面:考虑对称性,选取初始模型的1/4作为设计域,取其6个控制点的法向坐标作为形状变量,其坐标改变量的上下限均为[-2,2];形状优化体积约束为整体体积的1.3倍。拓扑优化方面:分析模型的控制点为60×84,每个控制点的密度设置为设计变量,拓扑优化体积约束为整体体积的3/10。因此,形状-拓扑协同优化的总体约束为初始体积的39/100。作为对比算例,在经典等几何拓扑优化方法中,保持与形状-拓扑协同优化相同的体积约束,总体积的约束值是初始体积的39/100。

图13 均布载荷作用下的半圆柱壳
所提出方法与经典等几何拓扑优化方法下参数域内的DDF图在图14中给出,各自的迭代曲线与一些中间结构分别如图15与图16所示。从形状-拓扑协同优化结果中可知,形状优化方面:设计域改变的初始阶段存在振荡,之后迅速收敛,结构整体沿控制点法向方向外扩,由圆弧形变为“门”字形。拓扑优化方面:随着迭代进程的推进,两侧弧形结构开孔个数增加。与经典等几何拓扑优化结果对比可发现,结构没有中间连接部分,且两侧弧形开孔结构的倾斜角度减小。同时,对比两种方法下的最终目标函数值可知,在体积基本相同的条件下,等几何形状-拓扑协同优化方法下的应变能相对减小31.87%,提高了优化效率。

(a)等几何形状-拓扑协同优化方法

(a)形状优化结果C=1 037.260 2

图16 半圆柱壳的经典等几何拓扑优化结果C=4 456.149 7
为了更清晰地观察结构形状变化,形状-拓扑协同优化方法下优化前后的控制点坐标在表3中给出。根据对称性可知,上下边界中控制点的x向、y向坐标变化一致,中线控制点的变动较大,结构整体弧度减小,最终演化为“门”形结构。
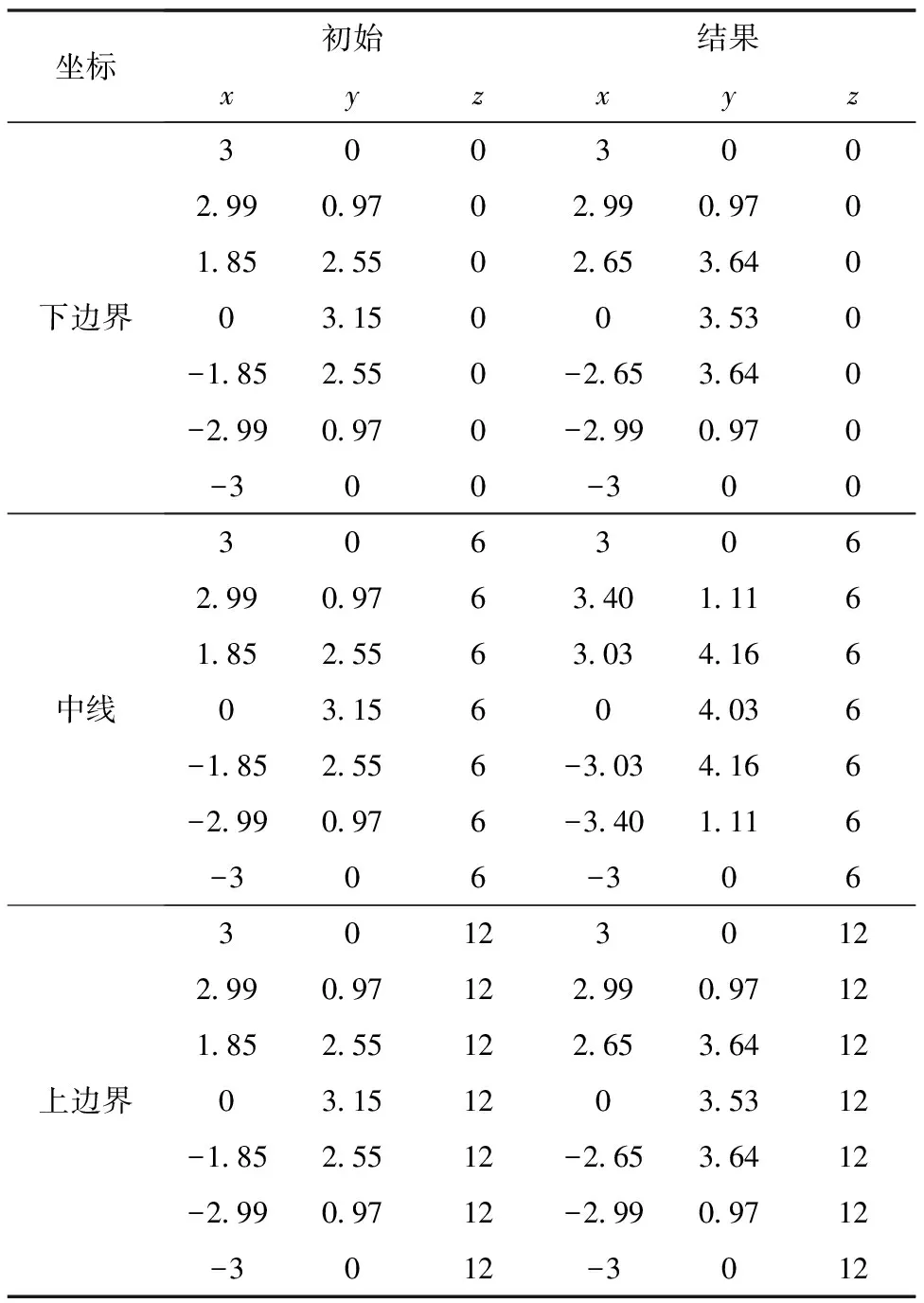
表3 半圆柱壳优化前后控制点坐标
4 结束语
本文提出了基于等几何分析的壳体结构形状-拓扑协同优化框架,可以找到板壳结构的最佳结构形状与最佳材料布局。在该过程中,等几何形状优化方面,推导了解析灵敏度公式,采用多水平模型说明了形状变化过程中的灵敏度传递问题;等几何拓扑优化方面,推导了灵敏度公式,考虑了过滤与投影以防止出现棋盘格与网格依赖性问题。最后,在MBB梁的经典算例中,与前人不同组合优化方法以及与经典等几何拓扑优化方法相比,所提出方法可以实现具有改进性能的优化解决方案;之后在受集中载荷自由曲面与受均布载荷半圆柱壳的数值算例中,通过与经典等几何拓扑优化方法下的结果进行对比,验证了所提出方法的有效性与高效性。

