薄壁加筋壳强度变差系数仿真预估方法研究

徐卫秀，杨 帆，蒋亮亮，吴会强，郝 鹏

(1.北京宇航系统工程研究所，北京 100076；2.大连理工大学工程力学系工业装备结构分析国家重点实验室，大连 116024)

0 引言

强度变差系数是结构可靠性设计与分析的重要参数，是开展可靠性安全系数量化设计、结构可靠性分析评估的重要依据。对运载火箭这类大型结构，受成本限制，通过试验获得整个部段的强度数据很少，一般只有1～3个，很难获得其强度变差系数。现阶段运载火箭结构可靠性设计、评估参考的仍为20世纪六七十年代的数据。半个多世纪以来，随着材料体系、制造加工工艺、产品测量、设计分析等技术的发展，影响运载火箭结构强度散差因素的不确定性和获取能力都发生了相应变化，非常有必要基于运载火箭结构研制设计、制造加工工艺现状应用新技术研究预估强度变差系数新方法。

薄壁结构理论强度由材料强度、刚度性能，结构尺寸参数确定，实际工程中，受制造、加工过程材料性能、结构尺寸、几何形貌随机不确定性影响，同一结构不同产品的强度有一定的散布。材料性能、结构尺寸的不确定性较容易通过真实测量数据统计表征，对金属材料强度、弹性模量数据及加工的结构尺寸一般能较好地符合正态或近似正态分布[1-2]。几何形貌的偏差又常称为初始几何缺陷，是引起受压薄壁结构屈曲失效极限强度分散性的关键因素[3-4]，一直是相关行业研究的热点[5-9]。几何缺陷测量技术最早可追溯到20世纪50年代[10]，经历了从接触式到非接触式测量方法的发展，目前应用广泛的为非接触式光学形貌测量技术[11-13]，表征圆柱壳缺陷应用最广泛的为纵向半波、环向整波双重傅立叶级数分解法[11，14，20]。2007年起，NASA[15-18]历时十余年开展了壳体屈曲折减系数(SBKF)项目研究，基于考虑初始几何缺陷的现代精确仿真分析技术，研究开发了现代运载火箭结构屈曲折减系数和设计分析技术，并以8 in(1 in=25.4 mm)缩比和27.5 in全尺寸贮箱网格加筋结构为例，开展了相关试验验证研究。我国大连理工大学王博教授团队联合北京宇航系统工程研究所也开展了相应技术研究[19-20]，对1 m直径整体机加成形光筒壳的初始几何缺陷进行测量，并引入到理想形貌有限元模型，实现了考虑初始几何缺陷的精确仿真分析技术，取得了很好效果。

在实现结构强度精确仿真基础上，预估强度变差系数的关键，是实现结构极限强度的模拟打靶计算。对存在明显非线性的薄壁结构后屈曲强度问题，直接采用有限元分析方法开展极限强度模拟打靶效率很低。对于复杂系统的不确定性问题，为简化计算，常采用基于概率分析的随机扩展法建立响应和变量不确定性间的代理模型，如混沌多项式展开法(PCE)、Karhumen-Loeve(KL)变换法等[21]，来实现基于代理模型的快速仿真打靶。

本文基于运载火箭结构研制现状和当前设计手段，提出了基于产品数据的强度变差系数仿真预估技术。以当前应用广泛、性能稳定，从材料体系、制造加工工艺、设计分析手段等方面都得到改善的运载火箭金属薄壁网格加筋壳为对象，开展相关实现技术研究。提出了实现技术途径；结合试验产品研制，测量统计材料性能、结构尺寸和几何形貌的不确定性；建立参数化有限元模型，实现考虑初始几何形貌的结构轴压极限强度精确仿真分析方法；采用多项式混沌展开代理模型实现薄壁结构极限强度的快速仿真打靶和强度总体变差系数的预估；并开展了3件1 m直径网格加筋圆筒壳轴压强度破坏试验验证研究。该技术研究旨在利用当前结构精细化设计分析能力，拓展运载火箭结构产品可靠性相关数据获取途径，实现对结构可靠性安全系数的精确量化设计，挖掘结构承载潜力。

1 试验件设计

试验件为图1所示的1 m直径正置正交网格加筋壳。结构设计时，综合考虑蒙皮厚度加工工艺最小尺寸和加工精度保证能力，为避免尺寸过小引入的蒙皮厚度不确定性过大，首先确定蒙皮厚度为2.0 mm；其他网格尺寸参数根据轴压载荷作用下的蒙皮局部屈曲、整体屈曲和材料屈服3种失效模式的等强度优化设计确定。壳体长度在满足中长壳要求的基础上，考虑上下对接需要确定。原材料和成型加工工艺，为2A14T6铝合金环轧锻造成型，五坐标机械铣加工。为实现统计验证，策划了3件产品，分别用SJ1-SJ3表示。

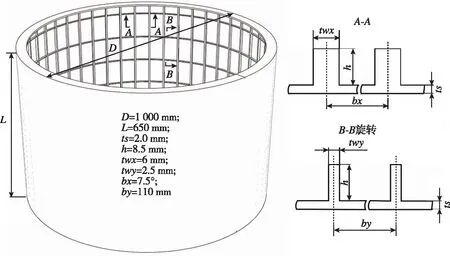
图1 正交网格加筋壳几何尺寸

2 研究内容及实现技术途径

研究内容及实现技术途径如图2所示，主要包括：

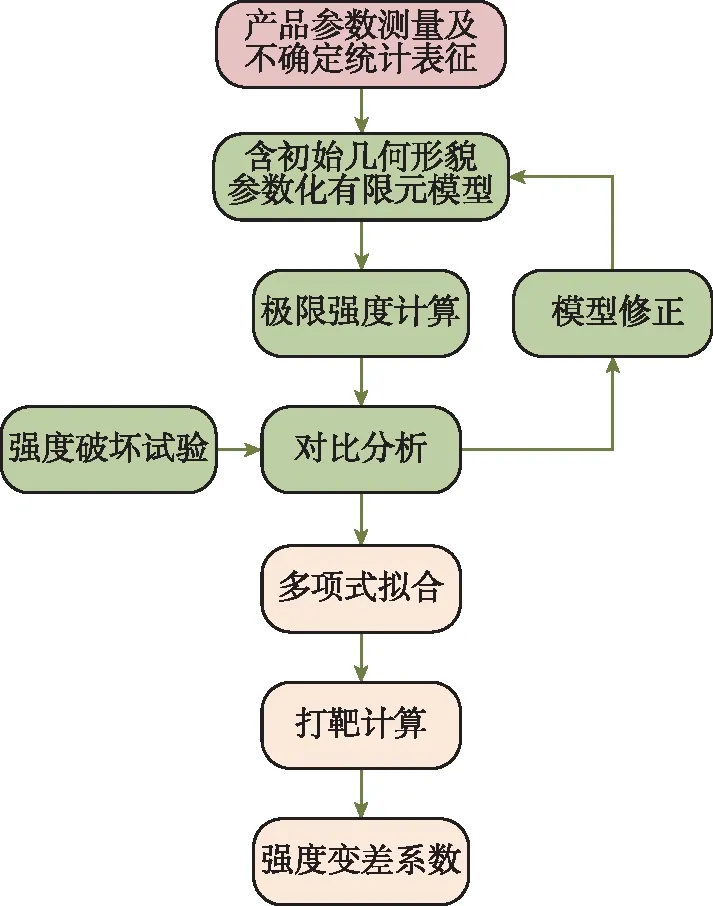
图2 实现技术流程图

1)产品本体材料性能、主要结构尺寸及初始几何形貌测量及不确定统计表征；

2)含初始几何缺陷参数化有限元模型的建立，极限强度仿真及其与试验结果的对比验证；

3)参数敏感性分析，有限元仿真采样，多项式代理模型系数求解及回归拟合；

4)多项式代理模型模拟打靶、强度变差系数预估及相关性分析等。

3 参数测量及不确定性表征

3.1 材料性能、结构尺寸的测量及表征

材料性能方面，考虑到锻件三向性能的不同，测量了轴向极限强度Rm、屈服强度Rp0.2、弹性模量E及延伸率δ等参数；结构尺寸方面，测量了壳体长度L、直径D，网格蒙皮厚度ts、筋条高度h、纵筋和横筋宽度twx和twy。强度和弹性模量的测量精度要求为0.01 MPa，延伸率测量精度为0.01%，尺寸测量精度为0.01 mm。

材料性能和结构尺寸采用正态分布表征，先检验数据是否符合正态分布，将不符合正态分布的数据转换为近似正态分布。统计获得的主要变量分布参数如表1所示，材料性能中屈服强度变差系数最大，为0.049；结构尺寸中蒙皮厚度变差系数最大，为0.025 5。

表1 主要变量分布参数

3.2 几何形貌的测量及表征

几何形貌测量、点云数据处理及表征方案如图3所示。测量采用了机械臂加激光扫描头方案。扫描前需先建立合理坐标系，用于点云数据处理和将几何缺陷正确引入到有限元模型中。扫描获得百万点云数据后，根据有限元模型节点规模适当精简，将坐标转换到有限元模型坐标系；经滤波降噪处理，与理论外形相比获得初始几何缺陷(离面位移)。

图3 几何形貌测量和表征方案

已有研究表明，表征圆柱壳初始几何缺陷最好的方法为轴向采用半波余弦、环向采用整波的双重傅立叶级数方法[11，14，20]，在柱坐标系下可表示为

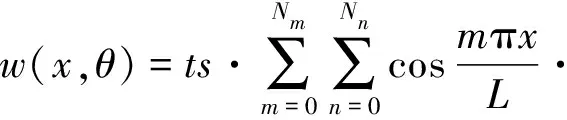
(Amncosnθ+Bmnsinnθ)

(1)

其中，w为离面位移，L为筒壳的名义高度；x为轴向坐标，θ为环向坐标(角度)；Amn和Bmn为傅立叶级数的系数。

图4为测量获得的3件试验产品离面位移云图，方向有凹有凸，大小随空间分布比较随机。SJ1产品偏差最大，最大值为蒙皮厚度的13/50，SJ2、SJ3产品相对较小，最大值不到蒙皮厚度的1/10。

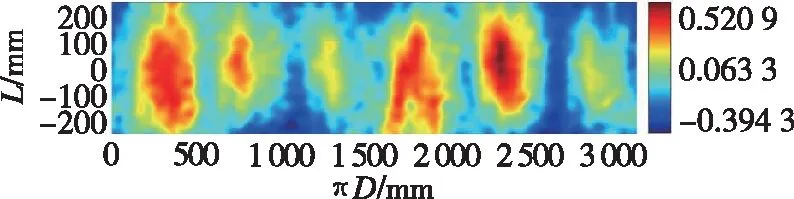
(a)SJ1

4 考虑初始几何缺陷的极限强度精确仿真

4.1 含几何缺陷参数化有限元模型建立

将结构几何简化为壳，应用Python脚本建立参数化有限元模型，采用S4单元模拟。为捕捉到薄壁结构后屈曲失效模式，采用显式动力学非线性方法求解[22]；为保证分析结果的精确性，对网格大小及计算时间进行了收敛性分析。

在Python环境下，利用Abaqus内置函数得到理想形貌有限元模型各节点坐标，按傅立叶级数拟合好的离面位移曲面，对各节点坐标进行偏移，实现形貌偏差的引入。包含初始几何缺陷的有限元模型如图5所示。

图5 含几何缺陷有限元模型(放大60倍)

4.2 结果对比验证

仿真分析了每件试验产品材料性能，结构尺寸取实测数据统计平均值，考虑初始几何缺陷前后的轴压极限强度，用承载能力T表征。

为获得试验件失效过程，试验采用了DIC数字图像测量系统，应用数字图像技术拍摄结构在不同载荷作用下的照片，通过对比照片中像素点灰度值的变化，观测结构形貌。

3件产品均为结构整体失稳破坏。仿真和试验轴压强度结果对比见表2。SJ1、SJ2、SJ3考虑初始几何缺陷(真实形貌)后的仿真与试验偏差分别为8.76%、5.21%、4.12%。用DIC数字图像测量系统对失效后形貌保持相对完整的SJ1、SJ2进行了测量，如图6所示，SJ1存在失稳波形分布不均、部分区域未失稳的情况，这可能是其试验强度低，仿真与试验偏差最大的原因。SJ2、SJ3的偏差接近，图7为SJ2仿真和试验轴压载荷-位移曲线和失效模式对比，曲线斜率和失效模式都吻合。

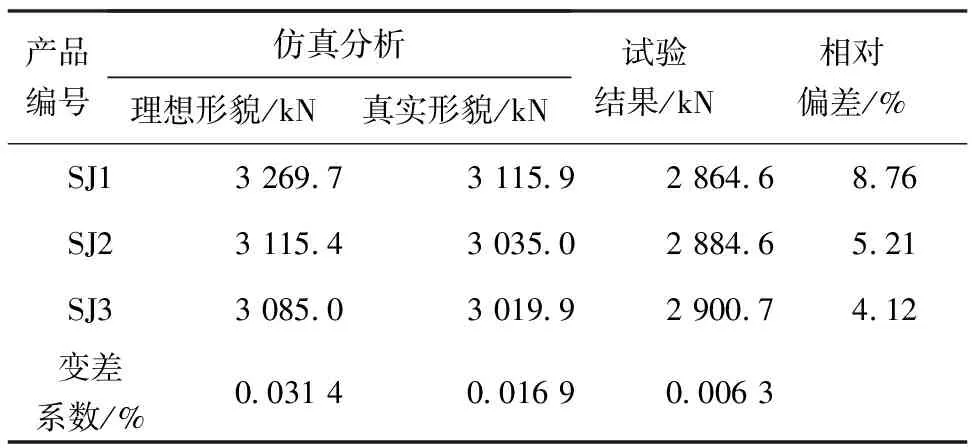
表2 轴压极限强度对比

(a)SJ1

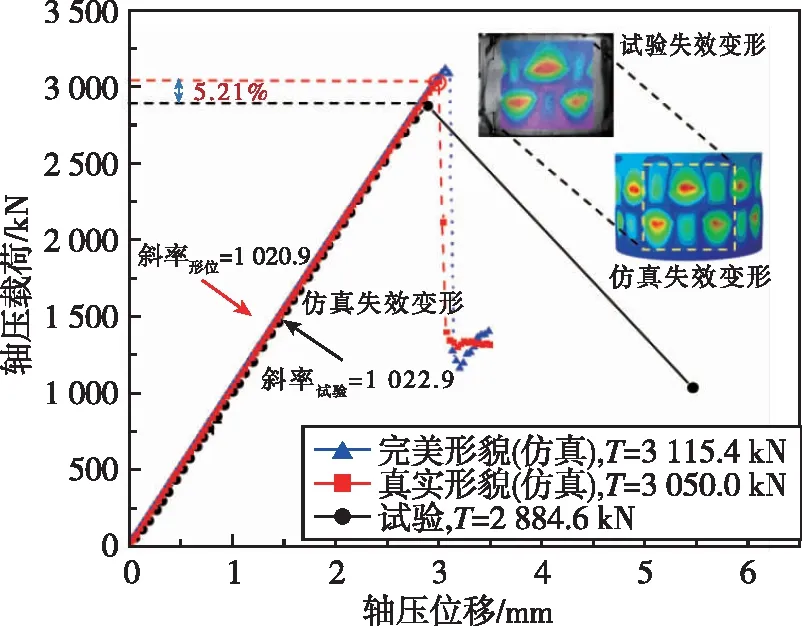
图7 SJ2轴压载荷-位移曲线及失效模式对比图

考虑到还存在有限元模型简化、试验不确定性等因素，未做修正的仿真结果相对试验偏差最大值小于10%，可以认为实现了极限强度的精确仿真。

由3个试验数据获得强度样本变差系数为0.006 3；仿真分析结果预估的强度样本变差系数为0.016 9，覆盖了试验值。同时，根据3个样本考虑真实形貌前后分析结果的折减，预估3件产品形貌不确定性引起的变差系数为0.014 3。

5 多项式打靶及强度总体变差系数预估

总体变差系数可通过逐个产品数据统计仿真积累方式获取，但需要足够的产品数量和相对较长的时间。这里假设结构制造加工工艺比较稳定，探索一种通过相关变量统计数据仿真打靶预估方法，主要考虑材料性能、结构尺寸参数在统计数据范围内的不确定，不考虑其随空间分布的变化，打靶获得材料、尺寸偏差引起的变差系数上限。在此基础上考虑几个样本形貌引起的变差系数，估算强度总体变差系数上限。

因薄壁结构极限强度有限元分析需要考虑材料非线性、几何非线性，仿真计算一次需要的时间较长，直接通过仿真打靶效率很低，提出了应用混沌多项式代理模型快速模拟打靶计算方案。

混沌多项式扩展法(PCE)是工程上应用广泛的不确定性拟合分析方法。与常规的多项式拟合不同，混沌多项式扩展法将随机变量转换为标准正态分布变量，并采用Hermite正交基函数，具有良好的均方收敛特性，能更好地估计不确定系统响应的变差特性[21]。具体实施流程如图8所示。

图8 薄壁结构非线性屈曲强度打靶流程

5.1 变量对强度影响分析

考虑材料弹性模量、屈服极限、极限强度、蒙皮厚度、筋条高度、纵筋和横筋宽度尺寸共7个参数的随机变化特性，为了解各参数对强度的影响关系，分析了承载能力随各参数在均值和正负3倍标准偏差(μ±3σ)范围内的变化情况(其他参数取均值)。分析表明，强度随弹性模量E、屈服强度Rp0.2的变化存在较弱的非线性，其他参数基本为线性关系。

5.2 采样计算

根据影响分析结果，确定弹性模量、屈服强度2个参数采用2阶多项式，其他参数采用线性拟合。

根据n个随机变量，p阶Hermite多项式展开总项数P计算公式[21]

(2)

7个随机变量，2个参数2阶、5个参数1阶的多项式为31项，按2倍样本计算，需要62个采样点。应用拉丁超立方采样方法生成7个参数的62组随机变量，将每组变量代入理想形貌参数化有限元模型中，仿真获得对应的极限强度响应，实现采样。

5.3 多项式拟合及回归分析

将随机变量和对应的强度响应代入公式(3)[21]，即可得拟合多项式系数B*

B*=(XTX)-1XTY

(3)

式中，X为n×P维的回归变量矩阵，Y为n×1维的系统响应矢量。

进而可获得拟合响应Y*和残差e

Y*=XB*

(4)

e=Y-Y*

(5)

从而可对回归方差和残差进行分析，检验代理模型的拟合精确度。

整个过程通过Matlab程序执行，多项式的拟合优度R2达到0.998 2，调整的R2达到0.997 9。

5.4 强度打靶及总体变差系数预估

应用混沌多项式打靶10万次获得的极限强度分布如图9所示，基本仍符合正态分布，说明结构极限强度随材料弹性模量、屈服强度参数的变化无明显非线性。

图9 10万次打靶数据分布

预估的极限强度变差系数及相关性分析结果见表3。材料、尺寸不确定性引起的强度变差系数为0.042 8。其中与材料部分的相关性为77.83%，主要由屈服强度引起；尺寸部分的相关性为22.5%，主要由蒙皮厚度引起。

表3 强度变差与各参数不确定性的相关系数

在考虑材料、尺寸不确定性预估的强度变差系数0.042 8基础上，综合考虑形貌不确定性引起的强度变差系数0.014 3(3个样本预估值)，可得到强度总体变差系数预估值为0.045 1。

5.5 结果分析

与试验样本变差系数相比，仿真预估的总体变差系数达到7倍以上，高于正态分布变差系数上限的放大系数3.12[4]，具有较高的可靠性。但相对历史统计数据0.08～0.12[4]，有较大程度的降低。

仿真预估的强度总体变差系数中，因实际结构产品材料、尺寸的不确定性是随空间分布的场变量，这里简化为参变量，认为产品各处的材料、参数尺寸相同，包含整个结构一个或多个变量参数同时达到上下偏差的极限情况，这比工程实际情况更为恶劣，材料、尺寸不确定性打靶预估部分相对保守；但形貌部分只考虑了3个样本数据，包络不了产品总体情况，需要随产品数量增加逐步积累完善。

6 结论及展望

本文针对运载火箭大型薄壁结构强度变差系数获取困难问题，实现了一种基于产品实测数据仿真预估结构强度变差系数方法。试验结果表明，预估的结构强度变差系数具有较高可靠性的同时，相对历史统计数据，有一定幅度降低，为降低安全系数、减小结构质量提供了有力数据支持。

文中极限强度仿真打靶仅考虑了材料性能、结构尺寸的不确定性，后续可根据同类结构统计的初始几何缺陷幅值及分布特征，开发产品形貌不确定性随机抽样技术，实现考虑材料性能、结构尺寸和几何形貌3大类不确定性打靶，进一步提高强度变差系数仿真预估精度。