面向大型承载结构强度性能的试验系统高精度装配调控方法

周才华，王 博，柯熊钢，郝 鹏，杜凯繁

(大连理工大学工业装备结构分析优化与CAE软件全国重点实验室，大连 116024)

0 引言

大型承载结构作为运载火箭[1]等大型装备结构的主要骨架，其试验技术成为大型装备结构的重大关键技术之一。同时，随着大型装备结构朝着大型化、精细化以及承载能力极端化方向发展[2]，大型承载结构强度试验考核愈发接近结构的承载极限，且更加关注试验的量化结果，试验系统的装配测量和调控精度的要求也随之增高[3]。因此，面向大型承载结构强度性能考核试验开展高精度装配调控方法研究，对提升试验考核精度非常重要。

近年来，传统量化大型承载结构试验装配精度的方法主要依赖于技术人员通过传统测量手段对结构装配位置与误差进行测量，无法精准保证装配位置的同时，也难以量化装配误差[4-5]，导致试验结果无法实现对大型承载结构的精细化考核。在控制装配精度方面，国内外已有大量的方法，其中不可或缺的技术便是坐标精确测量、定位以及装配误差值的获取与降低。如商飞公司采用光学扫描的方法，克服了复杂环境下大型承载结构间装配间隙难以测量的难题[6]，以及利用数字化测量方法量化舱段类大部件在装配中的变形及装配误差[7]。An等[8]针对微小零件提出一种三向正交视觉系统，根据零件特征检测零件的实时位置和姿态，实现装配过程的实时检测。工业上装配测量技术发展较为成熟，但相关方法鲜有在大型试验上得到应用。NASA采用铅锤测量方法对大型筒壳结构试验的装配精度进行测量[9]，此种测量方法虽能定位结构装配位置但无法量化结构装配偏差，影响最终考核试验结果分析。因此，借助工业上现有的成熟测量技术，将高精度测量技术应用于大型承载结构试验，对提高试验考核精度是十分必要的。

此外，提高大型承载试验考核精度不能仅依靠高精度测量方法，还需对试验系统中装配结构位置实现高精度控制。为提高大型承载结构试验考核精度，在大型承载结构试验中应用高精度调控方法，对实现大型承载结构高精度试验考核有重要的启发借鉴作用。如德国航空航天中心[10-11]针对筒壳结构试验采用自动液压夹具调整方法，对试验过程中的加载位置进行自适应调控，降低结构装配间隙误差，提高结构试验考核精度。另外，法国空客公司[12]以及巴西航空工业公司[13]为降低民机承载结构试验的加载误差，分别采用随动调控的方式对承载结构试验的加载位置进行实时调整，获得更为理想精确的试验结果。从上述内容可以看出，基于目前在工业装配领域中已获得成熟应用的调控方法，高精度调控方法也在大型承载结构试验加载过程中得到了进一步发展应用，而针对大型承载结构试验前装配位置的高精度测量调控却鲜有应用。因此，为更进一步提高大型承载结构试验系统装配精度并量化装配误差，亟须开展对大型承载结构试验系统的高精度装配调控方法研究，实现大型承载结构强度性能试验高精度考核。

本文以直径0.6 m开口筒壳为例，分析了相对位移误差、角度误差对仿真结果产生的影响，表明高精度量化试验系统装配方法研究的必要性。提出了装配调控方法框架及原理，开展了直径0.6 m开口、直径1.6 m筒壳装配精度调控试验，对比传统直尺测量方法，验证本文所提出方法的先进性。

1 试验系统装配误差对大型承载结构承载力影响

1.1 试验对象及建模

以直径0.6 m开口筒为例，分别研究装配位移误差、角度误差对结构承载能力影响。具体几何尺寸如图1所示，铝合金材料的弹性模量为70 GPa、泊松比为0.30、屈服强度为320 MPa。

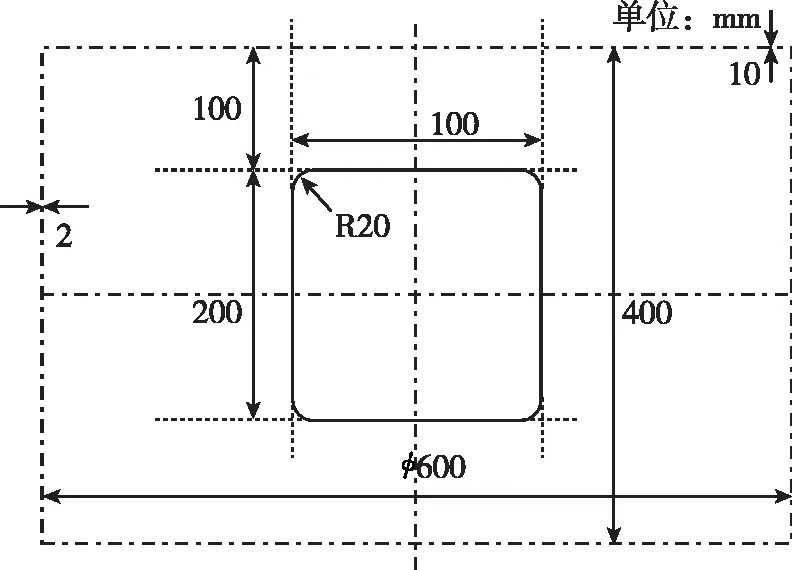
图1 直径0.6 m筒壳具体几何尺寸

建立筒壳承载力数值分析模型，如图2所示。下端框所有自由度固定、上端框耦合至参考点，固定参考点X，Y方向上的位移，放松Z方向的位移以及3个方向的转角，在参考点上施加3 mm位移，加载速度为40 mm/s，采用S4R缩减积分单元，网格数量为23 820个。

图2 开口筒壳承载力数值分析模型

1.2 位移误差对直径0.6 m开口筒壳承载力影响

为模拟装配位移误差对结构承载力影响，基于上述数值分析模型，通过改变参考点位置，从而改变加载点位置，实现不同装配位移误差下结构承载力分析。参考点y坐标依次取-25，-15，-5，0，5，15，25等值，计算得到筒壳承载力值结果如表1所示，y取0为表示装配位移误差为0，此时筒壳承载力为444.9 kN。表中结果显示，承载力误差随相对装配误差的增加而增加，因此，试验系统装配位移误差对结构承载力有一定程度的影响，且随着装配位移误差增加而增加。

表1 装配位移误差对承载力影响

1.3 角度误差对直径0.6 m开口筒壳承载力影响

为模拟装配角度误差对结构承载力影响，在进行轴向加载之前，在端面施加转角位移θ(绕Y轴旋转)，通过改变转角位移大小，实现不同装配角度误差下结构承载力分析。分别设置0°，0.04°，0.08°，0.12°，0.16°，0.20°角度装配误差，计算得到筒壳承载力值结果如表2所示。角度为0.20°时承载力降低了约38.2%，且极限承载力随角度误差增加而降低，表明装配角度误差对筒壳承载能力具有显著影响[14]。

表2 装配角度误差对承载力影响

2 高精度大型承载结构试验系统装配调控方法

2.1 试验系统高精度装配过程

试验系统高精度装配调控过程如图3所示。首先，测量试验平台标识点位置坐标，建立局部坐标系(测量设备)和整体坐标系(试验平台)转换关系。其次，测量装配件标识点坐标，建立装配件理论和实际位置转换关系。进而，基于装配件实际与理论位置坐标系转换关系，计算实际与理论位置的装配误差，若装配误差不满误差要求，则需结合机械推动以及位移测量等设备实现装配位置调控，调控完成后还需再次执行试验件位置测量、转配误差分析、位置调控等步骤，直至满足误差要求，则装配调控结束。

图3 试验系统高精度装配调控

2.1.1 测量试验平台标识点坐标

为统一局部坐标系(测量设备)和整体坐标系(试验平台)，需建立局部坐标系和整体坐标系之间的坐标转换关系。设定试验平台与试验件的整体坐标系，利用标识工具在试验平台上设置3个以上标识点，如图4 (a)所示，计算标识点整体坐标，通过测量设备依次测量标识点坐标，如图4 (b)所示，从而获取试验平台上全部标识点局部坐标。

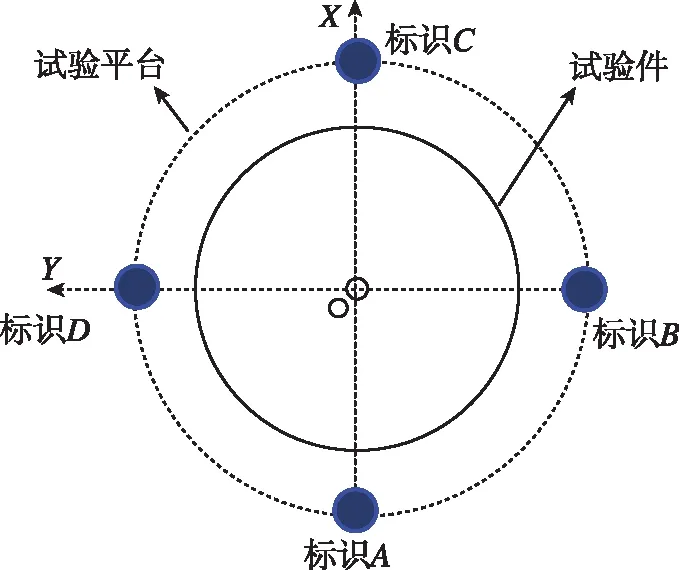
(a)选取试验平台3个以上标识点

2.1.2 建立整体和局部坐标转换关系

根据试验平台的n1个标识点整体坐标Pn1×3和局部坐标Qn1×3，建立两者坐标系之间的转换关系，见公式(1)，即求解旋转矩阵R3×3、平移矩阵T1×3，进而测量设备测量所得局部坐标均可转化为平台上的整体坐标。

Pn1×3=R3×3×Qn1×3+T1×3

(1)

2.1.3 测量装配件标识点坐标

在试验件上设置3个以上标识点，如图5 (a)所示；且其理论坐标已知，如图5 (b)所示；测量设备依次测量标识点坐标，如图5 (c)所示，从而获取试验件上全部标识点实际坐标。

(a)选取试验件标识点

2.1.4 建立理论和实际位置转换关系

根据装配件的n2个标识点理论坐标pn2×3和实际坐标qn2×3，建立两者坐标系之间的转换关系，见公式(2)，即求解旋转矩阵r3×3、平移矩阵t1×3，进而为计算装配件实际与理论位置误差提供数据。

pn2×3=r3×3×qn2×3+t1×3

(2)

2.1.5 装配误差分析

根据装配件理论和实际位置坐标系转换关系，计算装配件实际与理论位置位移误差Δd、角度误差Δθ，如图6 (a)所示。

2.1.6 装配位置调控

根据装配件实际位置与理论位置误差，对装配件进行调控，计算判断装配件的装配误差是否满足要求。若装配误差满足要求，如图6(b)所示，调控结束。若装配误差不满足要求，重复执行上述步骤。如此反复循环，直至装配件实际和理论坐标系之间误差满足要求，调控结束。

2.2 装配件理论与实际位置转换关系

针对三维空间中n个点，全局坐标系下(理论坐标)坐标描述为p1，p2，…，pn，局部坐标系下(实测坐标)坐标描述为q1，q2，…，qn，见式(3)，这两组坐标之间关系表达式是：Q=RP+t。装配件加工误差、测量误差导致R和t存在误差，为了减小R和t的误差，本文通过引入多个位置点，并基于最小二乘方法[15]的思想来求解最优的坐标系位置关系参数R和t，问题描述如式(4)所示。

(3)

(4)

式中，w代表权重系数，且w1+w2+…，+wn=1。

计算平移矩阵t，假设矩阵R不变，构造最小二乘函数F(t)，见式(5)，将F(t)对t变量求导得式(6)，得到t的表达式(8)，将t代入式(5)得式(9)。

(5)

(6)

求导结果为

(7)

(8)

(9)

对点集pi和qi做一个减中心点的预处理得式(10)，代入式(9)，接着寻找矩阵R的最优解。

(10)

(11)

假设R为正交矩阵，I为单位矩阵，即有

RTR=I

(12)

公式(11)简化后旋转矩阵表达式为

(13)

因xi，yi为d维列矢量，RT是d维方阵，有

(14)

(15)

矩阵R的最优解即为求解式(16)最小值

(16)

因此，需求tr(WYTRX)的最大值，作如下变化

tr(WYTRX)=tr((WYT)(RX))=tr(RXWYT)

=tr(RS)=tr(RUΣVT)

=tr(ΣVTRU)

(17)

U，R，V，M=VTRU是正交矩阵，意味着M列矢量为标准正交矢量，则有

(18)

要求值最大，必须使mii的值等于1，而M是正交矩阵，则M是单位矩阵，得到旋转矩阵

I=M=VTRU⟹V=RU⟹R=VUT

(19)

通过判断R行列式值进一步判断R是旋转矩阵还是反射矩阵。当det(VUT)=1时，R是旋转矩阵；当det(VUT)=-1时，R是反射矩阵。因此，R一般表达式为式(20)，带入式(8)得平移矩阵t。

(20)

2.3 装配件理论与实际位置误差

根据计算得到的旋转矩阵R和平移矩阵t，计算装配件位置误差Δd与角度误差Δθ。其位置误差为t，角度误差按照公式(23)进行计算[16]。

(21)

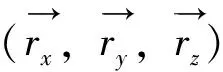
(22)

(23)

2.4 装配件理论与实际位置调控

装配件实际与理论的坐标系位移误差可以通过平移装配件进行消除，根据装配件理论与实际位置坐标系的位置偏差t，分别沿着X，Y，Z这3个轴方向进行平移。

但是角度误差不能用来定量指导装配件的角度调整。基于旋转矩阵R[17]中的9个变量只有3个是独立的，联立式(21)和(24)，求解α，β，γ，从装配件的角度调整步骤示意图如图7所示。

图7 实际与理论坐标系角度调整至重合过程

(24)

(25)

3 大型承载结构装配精度调控试验验证

3.1 强度试验高精度装配软件(Desk.EXP.AB)

对装配精控理论方法进行固化集成，开发强度试验高精度装配软件。该软件主要实现了3大功能。

该软件的第一部分功能为平台坐标系与测量设备坐标系的转换关系建立，作用是将测量设备坐标(局部坐标系)转换为整体平台坐标(整体坐标系)，如图8 (a)所示。

该软件的第二部分功能为装配件实际坐标系与理论位置坐标系的转换关系建立，作用是为装配件误差分析提供实际与理论相对位置关系，如图8 (b)所示。

该软件的第三部分功能为装配件实际与理论位置装配误差分析与调控，用于计算装配件实际与理论位置装配误差，为装配误差调控提供指导数据，如图8 (c)所示。

3.2 装配调控试验硬件设备

除了强度试验高精度装配软件，装配试验所需试验硬件设备如表3所示。其主要试验设备包括机械臂、标准球、热胶枪、千斤顶、激光位移传感器等，如图9所示。

表3 装配试验设备列表

图9 装配试验设备

3.3 直径0.6 m开口筒壳装配调控试验验证

基于装配调控软件与硬件设备，开展直径0.6 m 开口筒壳装配调控试验，该试验主要包括以下5个步骤。

3.3.1 基于传统方法进行试验装配与位置调控

为了对比本方法的精度，采用传统方法进行试验系统的粗装配，以该位置为试验系统初始装配位置。传统方法难以定量测量试验系统装配误差，因此，采用本方法进行初始装配精度测量。

3.3.2 建立机械臂坐标和平台整体坐标的转换关系

固定并明确机械臂坐标系和平台坐标系，并使用标准球在试验平台上建立特定数量的标识点，如图10所示。然后，过机械臂逐一测量标准球球心坐标，获得其在机械臂坐标系下的实测坐标。最后，将标识点平台坐标和实测坐标导入自研软件，建立机械臂坐标系和平台坐标系间的转换关系，如图11所示。

图10 设置标识点与坐标测量

图11 整体-局部坐标系转换关系建立

3.3.3 建立筒壳实际和理论位置转换关系

随后，在筒壳上选取一定数量的标识点，获得其在平台坐标系下的理论坐标，如图12(a)所示。通过机械臂逐一测量筒壳对应位置的标识点，如图12(b)所示。进而，通过上一步获得的转换关系，求得其在平台坐标系下的实际位置坐标。最终，将筒壳的理论坐标与实际位置坐标导入自研软件中进行计算，建立试验件在理论位置和实际位置的转换关系，如图13所示。

(a)设置标识点理论位置 (b)测量标识点实际坐标

图13 装配件实际和理论位置转换关系建立

3.3.4 误差定量分析

通过自研软件计算试验件理论和实际位置的初始装配误差，如图14所示。针对直径0.6 m筒壳试验进行装配误差定量分析，可为后续精度调控提供参考依据。

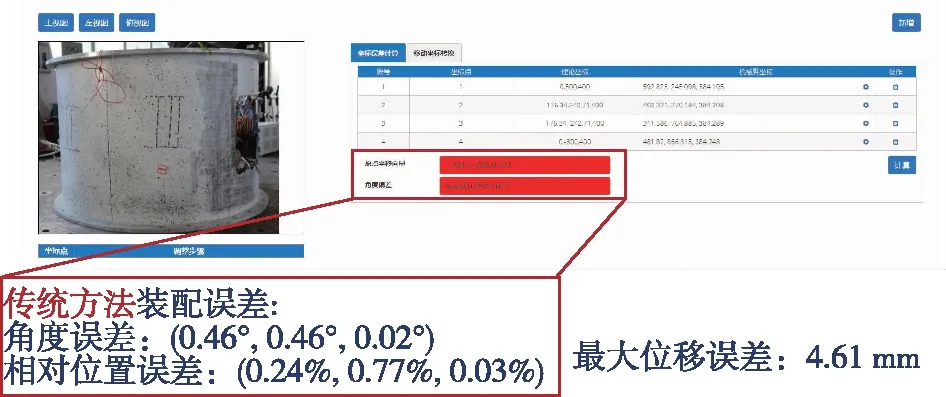
图14 传统方法的装配误差(直径0.6 m筒壳)

3.3.5 高精度位置调控

基于上一流程中计算获得的装配误差，借助辅助工具(千斤顶和激光位移传感器)对试验件进行调控，其调控方式如图15所示。进而，判断误差是否满足装配精度需求。若不满足精度则重复测量试验件位置、计算装配误差、装配位置调控，3次迭代后满足误差要求，调控结束，如图16所示。

图15 借助辅助工具进行位置调控 (直径0.6 m筒壳)

图16 本方法最终装配误差 (直径0.6 m筒壳)

传统方法与本方法装配误差的对比如表4所示。结果显示其最大相对位移误差从0.77%降至0.03%，最大角度误差从0.46°降至0.10°，最大位移从4.61 mm降至0.17 mm。

表4 传统方法与本方法装配误差对比 (直径0.6 m筒壳)

3.4 直径1.6 m筒壳装配调控试验验证

按照0.6 m筒壳相同的试验步骤进行直径1.6 m 筒壳装配调控试验，传统方法(见图17)与本方法(见图18)的装配误差结果对比如表5所示。结果显示其最大相对位移误差从0.94%降至0.05%，最大角度误差从0.93°降至0.04°，最大位移从15.00 mm降到了0.75 mm，实现了装配误差精度从厘米量级到毫米量级的提升。

表5 传统方法与本方法的装配误差对比 (直径1.6 m筒壳)

图17 传统方法的装配误差(直径1.6 m筒壳)

图18 本方法最终装配误差 (直径1.6 m筒壳)

3.5 计算实测装配误差对结构承载力影响

直径0.6，1.6 m圆柱筒壳与试验平台装配的结果见表4、表5，传统方法与本方法的Z轴角度误差均小于0.05°，这是装配件的加工制造缺陷、试验测量设备测量误差、转换关系中最小二乘算法等多种因素造成的。此外，考虑到圆柱筒壳在轴压载荷下，X轴、Y轴的角度误差不会对承载力造成影响，这里不考虑装配角度对结构承载力的影响。接下来，针对直径0.6，1.6 m圆柱筒壳，建立考虑实测装配位移误差的数值分析模型，计算传统方法与本方法装配误差下的结构承载力，如表6所示。传统方法数值分析承载力误差分别为1.67%、1.05%，本方法承载力误差仅为0.04%、0.00%。因此，基于本文提出的装配精度调控方法可以降低试验系统初始装配误差，以及装配误差对结构承载力的影响。

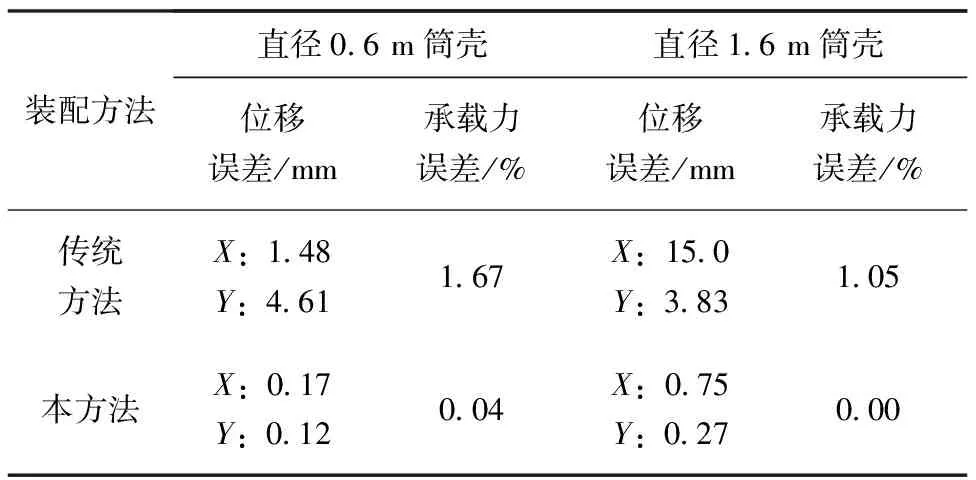
表6 传统方法与本方法装配误差导致的承载力误差对比(直径0.6，1.6 m筒壳)

4 结束语

本文以直径0.6 m开口筒壳为例，分别设置位移、角度误差进行结构承载力分析，分析结果显示，位移、角度误差对结构承载力有影响，且随着误差的增加而增加。为此，本文提出了一种高精度的试验系统装配方法，通过测量装配件实际位置，建立其理论位置与实际位置的坐标转换关系，并定量计算试验件实际与理论位置的位移误差、角度误差。本文提出的方法已经形成对应的强度试验高精度装配软件，可用于实际试验系统装配调控。

本文通过开展直径0.6 m筒壳、直径1.6 m筒壳两个装配调控试验，从定性的角度分析，相比传统直尺测量与位置调控，本方法具有装配误差定量分析的优势，实现了传统方法的装配误差从“不可测”到“定量测量”的转变。从定量的角度分析，直径1.6 m圆柱筒壳最大相对位移误差从0.94%降至0.05%，最大角度误差从0.93°降至0.04°，最大位移误差从15.00 mm降至0.75 mm，实现了装配误差从厘米量级到毫米量级的提升，降低了装配误差对承载力的影响。

随着试验件尺寸从直径0.6 m增加至1.6 m，试验件尺寸增长了近2倍，但其最大相对位移误差均不高于0.05%，最大角度误差不高于0.10°，表明本文所提出方法可以推广应用于未来直径更大的结构试验系统装配调控。