计及CVaR的含光热电站的鲁棒机组组合模型

张玉敏，吴福成，张少梅，吉兴全，钟世民，孙东磊

（1.山东科技大学电气与自动化工程学院，山东青岛 266590；2.山东科技大学电子信息工程学院，山东青岛 266590；3.国网山东青岛供电公司，山东青岛 266000；4.国网山东经济技术研究院，山东济南 250021）

0 引言

以风能为主的可再生能源发电系统大规模并入电网时，虽然可增加环境效益，但同时也增强了系统运行的不确定性与调度决策的难度[1-5]。光热电站（Concentrated Solar Power，CSP）是一种包含大容量储热系统（Thermal Energy Storage System，TESS）的新型发电技术，能够借助TESS 存储太阳能发电场（Solar Field，SF）转换的热能，在负荷高峰时段供电，解决太阳能发电间歇性的问题。该技术虽然增加了系统中光-热-电能量转化运行的复杂性，但由于其可充分挖掘CSP 的存储能力并有效提高能源消纳空间，使得CSP 技术得到了快速的发展[6-9]。

目前，提升电力系统中可再生能源消纳水平的灵活性资源主要包括CSP 的TESS 以及储能系统（Energy Storage System，ESS）。部分学者针对可再生能源并网发电所造成的不确定性问题进行研究，一种以ESS 接入系统提升可再生能源消纳水平为切入点，文献[10-12]搭建的含ESS 的机组组合模型表明，ESS 的接入提升了系统的经济性，为可再生能源提供了消纳空间。文献[13-14]构建的ESS 与可再生能源发电系统的调度模型表明，ESS 提升了系统对可再生能源的消纳能力。另一种以CSP 接入系统促进可再生能源的消纳水平为切入点，文献[15-18]构建含CSP 的机组组合经济调度模型，表明CSP 分担了常规机组的出力，提高了系统运行的灵活性。文献[19]搭建的CSP 机组与火电机组联合出力调度模型表明，CSP 机组促进了可再生能源消纳的能力，具有较好的经济效益和发展潜力。然而，文献[10-19]的研究仅考虑了CSP 和ESS 单独运行时对可再生能源消纳能力与经济水平的促进作用，未考虑CSP 与ESS 协同运行对提升系统经济性与可再生能源消纳水平的影响。因此，亟需提出一种包含CSP 与ESS 的鲁棒调度模型。

近年来，已有研究在调度决策过程中采用条件风险价值[20-23]（Conditional Value at Risk，CVaR）度量系统运行风险，通过提出一种计及CVaR 的发电调度模型，度量系统调度过程中可再生能源产生的风险损失，但其调度过程未考虑CSP 与ESS 协同运行对系统灵活性的影响。据此，本文提出一种计及CVaR 的含CSP 的鲁棒机组组合模型。推导了CSP机组的数学模型，并将其嵌入到计及CVaR 的含CSP 的鲁棒机组组合模型，同时采用分段线性化方法和列与约束生成（Column and Constraint Generation，C&CG）算法进行求解，降低了求解难度。算例分析表明，CSP 可以显著提升系统经济性和可再生能源的利用率。

1 含CSP的电网调度模型

CSP 采用双罐储热方式并以熔融盐作为储热与传热介质，受集热方式、运行方式等因素的影响，各个环节中均会产生能量损失。其中，SF 吸收的太阳能与镜片面积、太阳辐射强度等有关，当光照射到镜面时一部分光会被反射或透过，导致部分光照浪费；热存储过程中熔融盐由冷罐流至热灌，放热过程中熔融盐由热灌流入冷罐，冷热罐交替以及使用会造成热量损失；发电部分在实现热-电能量转化时，由于能量转化器的材料特性会造成一部分热损失。

CSP 主要由SF、TESS 和发电环节（Power Generation Process，PGP）3 部分组成，CSP 的主要结构与能量流动如图1 所示。

图1 CSP的主要结构与能量流动Fig.1 Main structure and energy flow of CSP

由图1 可知，SF 吸收反射太阳能再将其转换为热功率，实现光-热能量转换。所转换的热功率一部分随传热流体输送到PGP，实现热-电能量转换；另一部分随传热流体存储到TESS，依据系统的需求实现能量流动。

CSP 的能量流动指CSP 通过吸收太阳能热功率向系统提供电功率，同时借助TESS 存储热功率的过程，因此CSP 具有能量备用传递的功能。CSP的电网调度模型如式（1）—式（3）所示。

1）CSP 瞬时功率平衡约束为：

2）TESS 充、放热约束为：

2 计及CVaR 的含CSP 的鲁棒机组组合模型

2.1 条件风险价值

若调度周期内风力发电超出可消纳边界，可能产生一定的运行风险。定义风电功率超出系统最大调节范围产生的平均损失为条件风险价值，设风电功率预测误差的概率密度函数服从正态分布，如图2 所示。

图2 风电功率预测误差的概率密度函数Fig.2 Probability density function of wind power prediction error

如果风电场功率超出了系统接纳范围的上、下边界，需要采取弃风或切负荷措施，计算由弃风或切负荷所导致CVaR 的值R为：

由于式（4）中存在非线性积分表达，难以直接对其求解，故采用线性化方法处理式（4），详见文献[24]。

2.2 两阶段鲁棒优化模型

2.2.1 第1阶段鲁棒优化模型

第1 阶段鲁棒优化模型以机组的运行成本、系统运行风险成本以及启停成本之和最小为目标，其目标函数F1为：

第1 阶段鲁棒优化模型约束如式（7）—式（17）所示。

1）火电机组与CSP 机组爬坡速率及输出功率约束为：

2）火电机组与CSP 机组最小开停机时间约束为：

3）节点功率及功率平衡约束为：

式中：Nload为负荷总数；Pt,d为t时段负荷d的功率；Pt,ix,Pt,xi分别为t时段节点i到节点x和节点x到节点i的输送功率；ε(x,·)，ε(·,x)分别为节点x为起始节点的集合以及节点x为终止节点的集合。

4）线路容量约束为：

5）风险约束为：

式中：σda为日前风险目标门槛值。

6）ESS 充、放电约束为：

8）ESS 充、放电调控策略约束为：

2.2.2 第2阶段鲁棒优化模型

第2 阶段鲁棒优化模型目标函数F2是在不确定集合中最坏情况下使弃风与切负荷的成本最小，其表达式为：

第2 阶段鲁棒优化模型约束如式（19）—式（22）所示。

1）风电不确定性集合约束为：

2）节点功率及功率平衡约束为：

3）切负荷量约束为：

4）弃风量约束以及为：

第2 阶段约束还包括CSP 内部约束式（1-3）、电力网约束式（7-8）、式（12）、式（15-17）。

第2 阶段的表达形式是max-min 结构，不能像单层问题一样直接求解。所以本文利用对偶原理将内层最小化问题转换为对偶最大化问题，再与外层最大化问题合并成单层的最大化问题进行求解。通过上述线性转换后，模型变成混合整数线性规化问题，并采用改进的C&CG 算法求解。

3 算例分析

3.1 IEEE 6节点系统算例

本文以6 节点系统为例，分析鲁棒调度模型的有效性。算例中选取时间和空间上的置信水平分别为ϑTI=95%和ϑSP=95%。所以6 节点系统中不确定集合在时间和空间上的不确定度参数分别为ΓTI≈1 和ΓSP≈8。6 节点系统示意图如图3 所示。其中，G1—G3 为火电机组，wf 为风电场，L1—L3为有功负荷设备，Line1—Line7 为线路，模拟调度周期为24 个时段。

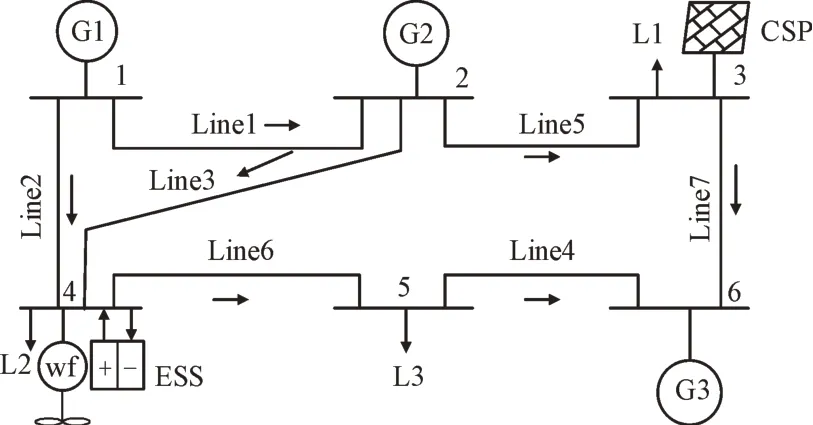
图3 IEEE 6节点系统示意图Fig.3 Schematic diagram of IEEE 6-node system

由图3 可知，在IEEE 6 节点系统中，火电机组、风电场、CSP 机组、ESS 为主要的供电设备，通过实现参与调度的机组出力与负荷的平衡，以实现系统最优经济调度的目标。

为分析CSP 机组对系统的影响，构建3 种鲁棒机组组合模型。模型1：不考虑CSP 和ESS 的鲁棒机组组合；模型2：仅考虑ESS 的鲁棒机组组合；模型3：考虑CSP 和ESS 的鲁棒机组组合。

3.1.1 调度结果分析

为分析CSP 对系统运行经济性的影响，对不同模型进行分析，得到3 种模型的6 节点系统调度成本如表1 所示。

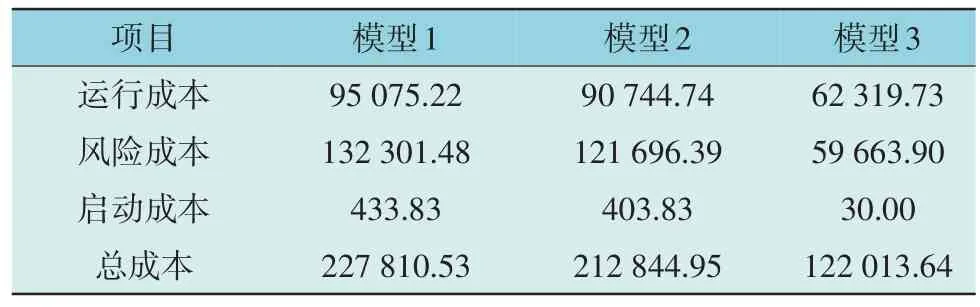
表1 3种模型的6节点系统调度成本Table 1 6-node system scheduling costs of three models $

由表1 可知，模型3 的运行成本较模型1 和模型2 分别降低了34.45%和31.32%，启动成本较模型1 和模型2 分别降低了93.1%和92.5%，表明引入CSP 之后大幅减轻了火电机组的运行压力、启停次数，有效提升了系统的运行经济性。模型3 风险成本较模型1 和模型2 分别降低了54.9%和50.9%，模型3 总成本较模型1 和模型2 降低了46.4%和42.6%，表明CSP 机组与ESS 协同运行有效促进了可再生能源的消纳，提升了系统运行经济性。

3.1.2 CSP参与调度的机组出力及TESS特性

为验证CSP 机组出力提供灵活性的能力，本节通过对模型3 优化结果进行分析，结果如图4 所示。由图4 可知，图4（a）中利用TESS 大量存储SF 转换的光热功率，逐渐减少CSP 机组出力，达到让风电出力，减少弃风量，降低系统调度成本的目的。图4（b）中CSP 初始储存热量较高，在1:00—5:00 时CSP 机组利用初始热量发电，以减轻机组负担。10:00 之后光照充足，SF 转换的热功率一部分用于负荷供电，另一部分存储到TESS 用于夜间发电。17:00 之后光照强度较小且逐渐为0，CSP 释放存储的热能继续出力，一方面保证了TESS 始末热量相等，另一方面满足负荷需求并维持系统平衡。CSP 机组结合TESS 灵活出力，显著地减少了火电机组的运行时间，减轻负荷高峰时段火电机组供电的压力。

图4 模型3优化结果Fig.4 Optimized results of model 3

3.1.3 机组组合结果分析

为分析机组组合受CSP 的影响，对3 种模型进行分析，得到模型机组组合决策结果如表2 所示。其中，1 表示开机，0 表示停机。

表2 机组组合决策结果Table 2 Decision results of UC

由表2 可知，3 种模型中最经济的火电机组G1在调度周期始终保持运行状态。模型1 中，成本较高的火电机组G2 在高峰负荷时段供能，这是由于模型1 不含ESS 与CSP，无功率存储部分，灵活性较差。模型2 中，ESS 参与系统供电，支撑电负荷需求，使得经济性最差的火电机组G2 在9:00—16:00与21:00—22:00 退出运行，仅在高峰负荷17:00—20:00 时段投入运行，从而节省了系统运行成本。相比于模型1 和模型2，模型3 中进一步考虑了CSP 机组，实现了光能、热能与电能的转换，缓解了火电机组的供电压力，使机组G2 在调度周期内始终停机，机组G3 只在负荷高峰18:00—21:00 时处于运行状态。这是由于CSP 可借助TESS 在电负荷高峰转化电能以满足电负荷需求，从而使成本较高的G2 始终保持停机状态，使G3 减少启动时间，通过减少机组运行时间达到缓解机组供电压力的目的，进一步提升了系统经济性。综上，说明同时考虑ESS 与CSP 可减少机组启动次数、缩短火电机组运行时间。

3.1.4 不确定度参数的保守性分析

为分析CSP 参与系统调度对模型保守性的影响，对模型2 和模型3 进行对比分析。通过对ГSP进行调控，可实现模型鲁棒性与保守性的调节，当固定ГTI=1 时，不同ГSP下的调度成本如表3 所示。

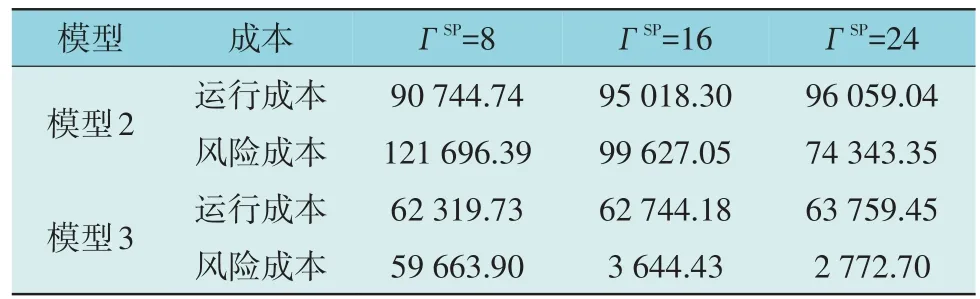
表3 不同ГSP 下的调度成本Table 3 Scheduling costs with different ГSP $

由表3 可知，随着ГSP的增加，模型的风险成本降低、运行成本增加。相比ГSP=8，在ГSP=16 和ГSP=24 时，模型2 的风险成本分别降低了18.13%和38.91%，模型3 的风险成本分别降低了93.89%和95.35%。表明CSP 的加入有效提高了风电消纳水平。

3.1.5 灵活性不确定集和消纳边界

为验证本文所建不确定性集合的边界是通过权衡风险损失与机组成本优化决策后所得，可有效提高对可再生能源的消纳能力，将模型3 决策所得的不确定性集合的消纳边界与文献[25]中传统鲁棒优化方法直接给定不确定性集合的消纳边界进行对比，得到不同模型风电功率的上下边界如图5所示。

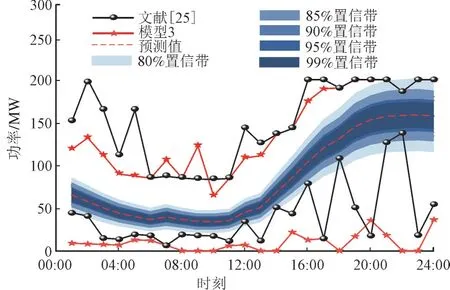
图5 不同模型风电功率的接纳范围Fig.5 Wind power consumption range of different models

由图5 可知，置信带上下2 部分曲线分别代表风电消纳的上下边界，相比文献[25]给定的上下边界，本文所提模型3 在多数时间段内的上下边界变动幅度较小，如在1:00—6:00 和12:00—15:00 等。结果表明，通过灵活调节可再生能源消纳边界可减少系统运行风险。

3.2 IEEE 118节点系统算例

IEEE 118 节点系统有3 个TESS、3 台CSP 机组、3 个风电场、3 个ESS、53 台火电机组，模型1—模型3 在CSP 参与调度的机组出力及TESS 特性、机组组合结果分析、灵活性不确定集和消纳边界的研究与6 节点系统类似，因此不在赘述。选取IEEE 118 节点系统的调度结果与不确定度参数的保守性进行分析，进一步证明CSP 的经济效益与促进可再生能源方面的优势，验证了模型和方法的有效性。

3.2.1 调度结果分析

3 种模型的118 节点系统调度成本如表4 所示。

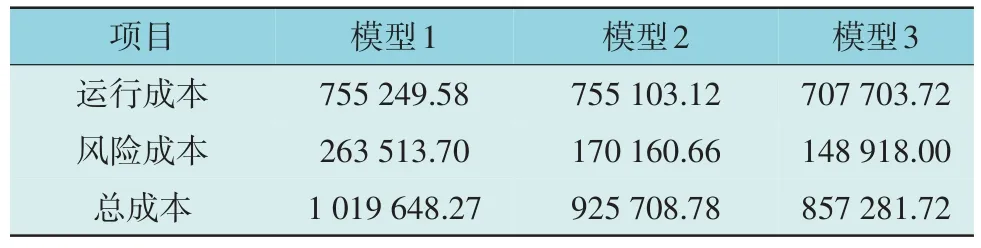
表4 3种模型的118节点系统调度成本Table 4 118-node system scheduling costs of three models $

由表4 可知，模型2 较模型1 的运行成本、风险成本和总成本分别下降了0.02%、35.4%和9.2%。模型3 的运行成本、风险成本和总成本在模型1 的基础上分别下降了6.3%、43.5%和15.9%。这是由于CSP 机组可通过TESS 灵活调整出力，降低系统的运行成本、风险成本与总成本，极大地提高系统经济性。

3.2.2 不确定度参数的保守性分析

为进一步验证不确定度参数对系统保守性的影响，得到不确定度参数组合下的调度成本如表5 所示。

表5 不确定度参数组合下的调度成本Table 5 Scheduling costs under uncertainty parameter combinations $

由表5 可知，在固定不确定度参数ГTI时，随着ГSP的增加，运行成本增加，风险成本和总成本降低；在固定不确定度参数ГSP时，随着不确定度参数ГTI的逐渐增加，运行成本降低，风险成本和总成本趋于增加。相比于模型2，添加CSP 机组的模型3 在不确定度参数ГTI不变时，总成本与风险成本随着不确定参数ГSP的增加而降幅明显增大，表明CSP 借助储热系统的灵活性为电力系统提供了能源优化空间，提升了系统经济性，降低了调度结果的保守性。

4 结论

本文通过分析CSP 的存储特性，提出一种计及CVaR 的含CSP 的鲁棒机组组合模型。通过算例分析证明了模型有效性，并得出如下结论：

1）CSP 结合ESS 可充分挖掘系统的灵活性潜力，缓解火电机组的供电压力以及提高经济性。

2）模型中风电不确定集合的边界是决策所得，通过灵活调整不确定性集合的消纳边界，可避免传统鲁棒调度结果的保守性。

本文所提模型并未考虑CSP 供给灵活性的详细模型，将在后续研究中进一步完善模型。