基于GM估计的电-气-热综合能源系统分解协调鲁棒状态估计方法
张爱军,刘紫玉,邢华栋,慕 腾,杜 翔
(1.国网内蒙古电力科学研究院,内蒙古呼和浩特 010020;2.内蒙古自治区电力系统智能化电网仿真企业重点实验室,内蒙古呼和浩特 010020;3.三峡大学电气与新能源学院,湖北宜昌 443000)
0 引言
众所周知,在电网中由于各个区域电网的技术和行业限制,对专有信息进行壁垒保护,互连电网子系统之间的实时数据很难共享,例如广东电网与香港电网互联,而双方对自身网络参数、完整潮流和拓扑结构等都视为机密,信息并不共享[1-3]。因此,为确保在线电力互联网络安全分析的准确性,一般采用不依赖于外部网络参数数据及其完整潮流信息的非拓扑静态等值方法[4-6]进行分析。
同理,在综合能源系统(Integrated Energy System,IES)中,完备的实时网络数据不能共享。在仅能交换边界耦合元件的数据信息情况下,此时集中式状态估计(State Estimation,SE)明显不再适用,而需采用分布式的SE 算法[7-10],各子系统单独计算,并通过边界条件最终获取系统全局一致解。
在文献[8]中提出用于电-气-热IES 系统的基于正交变换的分布式SE,在该估计模型中,与双线性的加权最小绝对值方法[11-15]类似将非线性方程实现线性化,然后通过交替向乘子法将集中式SE 转化为分布式SE。故而与集中式SE 方法相比,交替向乘子法可解决在缺乏统一数据中心、具有商业壁垒情况下的IES 系统SE。然而,该算法的构造基础是传统加权最小二乘(Weight Least Square,WLS),因而沿袭了WLS 的低抗差性。
统一联合SE,可将电气热联合估计,增加系统量测相关性,获得全局一致解[16-20]。文献[21]同时对电力系统和天然气系统融合考量,对两者构建的耦合系统进行稳态分析,并构建了稳态分析模型。文献[22]建立了热电联产系统模型。文献[23]研究了考虑电力、天然气和区域供热系统为一体的统一能流分析。然而由于商业隐私性和保密性,在缺乏全局网络结构、参数和数据信息情况下,统一联合SE难以实际进行[24-25]。
分解协调SE,可在各电气热系统相对独立、归属不同部门管辖,网络参数保密信息互不通畅情况下,仅需耦合元件的电气热网络边界数据,即可获得精度更高、吻合程度更高的全局一致解,有利于提升数据精度和准确度,且不需要系统参数完全互换,保持商业机密信息的相对独立。
为此,本文提出一种电、气、热相结合的IES 分解协调鲁棒SE 方法。该方法的创新之处在于:(1)考虑耦合元件边界条件约束,通过虚拟测量在电、气、热3 个子系统中的交互,将IES 的SE 分解为3 个独立子部分,实现集中式估计变为分布式估计;(2)通过耦合元件的能量转换计算节点解耦处的虚拟测量值,并加入到原始测量向量中反映子系统间的作用,依次求解电、热、气子系统的分解SE,直到估计结果满足全局收敛条件,实现高效求解。
1 IES量测模型
1.1 电力子系统量测模型
电力系统的量测量包含各节点注入功率(其中包括有功功率P和无功功率Q)、电压模值V和支路功率(支路有功功率为Pb,支路无功功率为Qb)。构建整个量测量为ze=[PQ V PbQb]T,状态量为各节点电压模值为V和相角θ,构建的整个状态量矩阵为xe=[Vθ]T。
量测量与状态量的方程可表示为:
式中:Pi,Qi分别为节点i注入的有功功率和无功功率;Vi和Vk分别为节点i、节点k处的电压模值;δik为节点i,k间的相位差值;Gik为节点i,k间支路的电导;Bik为节点i,k间支路的电纳;Ne为电网节点总数;Pik,Qik分别为节点i,k间支路的有功功率和无功功率。
1.2 天然气子系统量测模型
在气网中,量测量包含气节点压力平方π、管道支路流气量f和各节点流出流气量L,构建的量测量整体状态矩阵为zg=[πf L]T,状态量为各气节点压力平方,由xg=[ ]πT表示。
量测量与状态量的方程可表示为:
式中:fij为节点i,j间流气量;lgi为节点i气体流出量;σgi为与节点i相连的管道集合;πi为节点i压力平方;sij为节点i,j间天然气流向标识;pi,pj为节点压力,当pi>pj,为+1,当pi<pj,为-1;Kij为与管道有关的系数;q为与气体输送压力有关的系数。
1.3 热力子系统量测模型
在热力系统中,其稳态模型主要分为水力模型和热力模型2 类。
在水力模型中,针对节点注水量Ri和管道位置处储存水量mij建立的节点方程如下:
式中:hi,hj为节点压强;Gij为管道参数;pipe为节点集合。
在热力模型中,涉及的相关热负荷方程如下:
式中:ϕi为节点i热负荷;Tsi,Tri为节点i供应温度和返回温度;Cp为水比热容。
在热力系统网络中,包含的量测量为节点处的压强h、注水量R、不同节点间的水流量m、热力模型中热负荷ϕ、供应温度Ts及返回温度Tr,构建的整体量测量矩阵为zh=[hR m ϕ TsTr]T。
状态量则包含h,Ts和Tr,构建的状态量矩阵为xh=[hTsTr]T。
在热力模型中涉及的主要方程为:
2 IES分解协调状态估计模型
2.1 IES状态估计模型
2.2 耦合元件模型
在本文中,仅考虑热电联产机组(Combined Heat and Power Plant,CHP)单元作为耦合元件。CHP 单元的能量形式转换表达式为:
式中:ϕCHP为CHP 产热功率;PCHP为CHP 产电功率;cm为CHP 产热产电功率比;FCHP为天然气消耗量;cgas为天然气热值;η为CHP 效率。
考虑耦合元件边界条件约束,并将其作为虚拟量测,通过虚拟量测在电、气、热3 个子系统中的交互,将IES 的SE 分解为3 个独立子部分。
3 IES分解协调状态估计算法
本文将整个IES 解耦为电力、热力和天然气子系统,通过CHP 耦合节点的能量转换进行互联。因此,IES 的SE 可以分解为3 个相对独立的子系统SE,分别采用基于GM 估计的鲁棒SE 进行计算。
3 个子系统SE 之间的协调主要体现在CHP 节点虚拟测量的交互过程中,如图1 所示。
在各子系统的独立SE 中,根据其他2 个子系统的估计结果,通过CHP 耦合元件的能量转换计算,解耦CHP 节点的虚拟测量值,然后加入到各子系统的原始测量向量中,以反映子系统间的相互作用。
以电力子系统独立SE 为例,分别从热力子系统和天然气子系统获得CHP 节点的有功功率虚拟测量值,用于电力子系统SE。当电力子系统状态估计收敛时,则CHP 的电力输出估计值是已知的。然后,CHP 的热功率输出值和燃气消耗量可由CHP 耦合元件关系得出,并分别传递给热力和天然气子系统作为其SE 的虚拟测量值。
依次求解电、热和天然气子系统的分解协调SE,直至最终估计结果满足全局收敛条件为止,IES 鲁棒估计过程才算结束。全局收敛条件表达式如下所示:
式中:ε为收敛精度,设为10-5。
通过式(1)—式(9)分解协调鲁棒SE,各子系统可实现独立计算,只需交换耦合元件边界信息,即可通过协调获得IES 的全局最优估计。IES 分解协调SE 算法流程如图2 所示,其中y表示迭代次数,Ymax表示最大迭代次数。
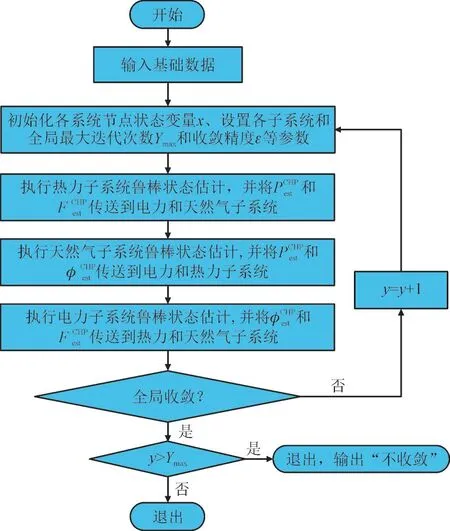
图2 IES分解协调状态估计流程图Fig.2 Calculation flow chart of decomposition and coordination state estimation for IES
4 算例仿真与分析
4.1 基础数据与仿真条件
基于图3 所示的电-气-热IES 系统[24-25],对本文所提电-气-热IES 系统分解协调鲁棒SE 方法的准确性、鲁棒性和计算效率进行验证。图3 中,CHP主要作用是将电、气、热3 个系统进行耦合。Nodee,Nodeg,Nodeh分别为电、气和热子系统中的节点。
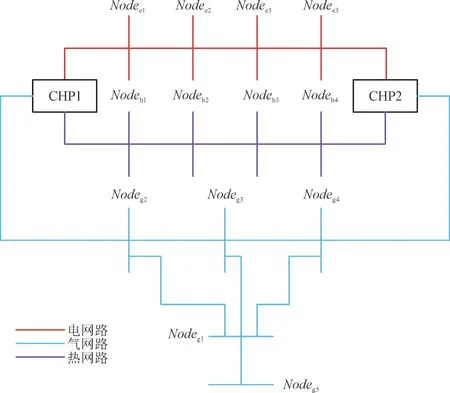
图3 电-气-热综合能源系统网络结构图Fig.3 Network structure diagram of electricity-gas-heat IES
本文采用ERx作为估计结果精度的评价指标:
式中:ERx为状态量x估计值相对真值的总体偏差;T为蒙特卡罗模拟次数;N为整个耦合网络涉及到的节点总数;n为第n个状态量估计值;xn,ture为第n个状态量真实值。
此外,以整个系统中存在的耦合元件建立边界等式约束,同时将S1和S2作为衡量耦合元件边界的指标,建立如下表达式:
式中:NCHP为涉及的CHP 元件总个数;ρ1和ρ2为边界匹配指标;t为第t次蒙特卡罗模拟;为节点i的CHP 产热功率;为节点i的CHP 产电功率;为节点i的天然气消耗量。
S1和S2数值越小,表明设立的边界匹配效果越好,越能反映实际情况。
在该系统中,量测值是完全测量结果,将其作为真值。此外,在量测值基础上叠加高斯噪声,则该叠加值可当实际测量值处理。基于蒙特卡罗模拟多次计算,蒙特卡洛模拟次数为2×103次。将基于WLS 的电、气、热各子系统单独SE 结果、基于GM 估计的集中式SE 结果与本文所提分解协调SE方法的结果进行对比。
4.2 仿真结果与分析
4.2.1 有坏数据时状态估计结果比较
将CHP1 单元的产电功率PCHP1量测设为原来的1.35 倍,产热功率ϕCHP1量测设为原来的1.25 倍,天然气消耗量FCHP1设为原来的1.30 倍,CHP1 的量测视为坏数据,并采用基于WLS 的单独估计、基于GM 的集中估计和本文所提分解协调状态估计方法分别进行计算,结果如表1—表3 所示。其中ERV,ERθ,ERπ,ERh,ERTs,RTr分别为节点电压模值、相角、压力平方、压强、供应温度、返回温度总体偏差,均为标幺值。
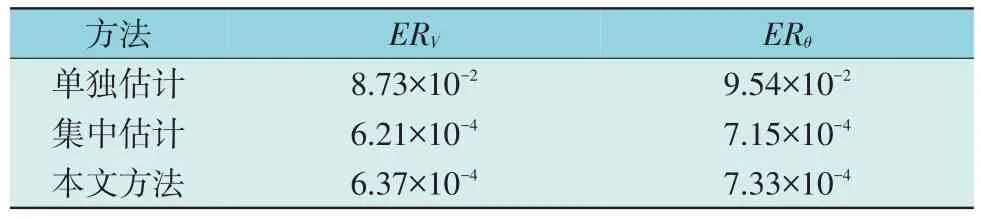
表1 有坏数据时电网状态估计结果Table 1 SE results of electric network with bad data

表2 有坏数据时气网状态估计结果Table 2 SE results of gas network with bad data
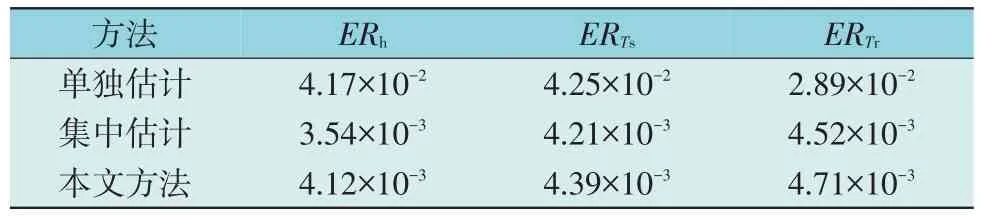
表3 有坏数据时热网状态估计结果Table 3 SE results of heat network with bad data
由表1—表3 结果可知,基于WLS 的单独SE结果ERx指标均较大,而集中式SE 方法和本文所提分解协调SE 方法ERx指标均较小,且均明显小于基于WLS 的单独SE 结果,说明本文所提分解协调SE 方法结果精度高,鲁棒性能好。
4.2.2 边界条件匹配情况比较
在无坏数据和有坏数据情况下,单独估计、集中估计和本文所提分解协调状态估计方法的耦合元件边界匹配指标如表4 和表5 所示,其中max(ρ1)和max(ρ2)为最大边界匹配指标,表中指标均为标幺值。
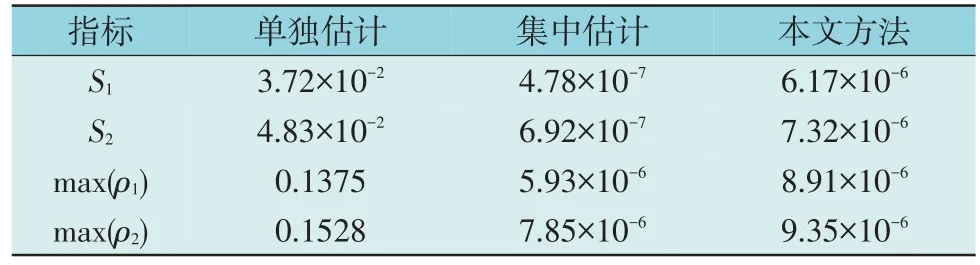
表4 无坏数据时边界匹配指标Table 4 Boundary matching indicator without bad data
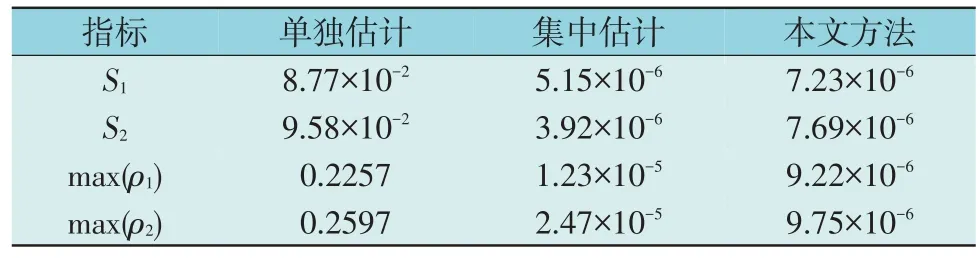
表5 有坏数据时边界匹配指标Table 5 Boundary matching indicator with bad data
由表4 和表5 可知,基于WLS 的单独估计耦合元件边界匹配指标均较大,所得结果不可避免地存在误差。由于集中估计可将耦合元件的边界条件作为等式约束,则该方法可以严格保证结果满足边界约束。本文方法在各子系统的独立SE 中,根据其他2 个子系统的估计结果,通过CHP 耦合元件的能量转换计算,解耦CHP 节点的虚拟测量值,然后加入到各子系统的原始测量向量中,以反映子系统间的相互作用。本文将耦合元件误差收敛阈值设为10-5,每次全局收敛只需满足边界匹配条件比10-5小即可,故而耦合元件的S1和S2和max(ρ1)和max(ρ2)始终小于10-5。
4.2.3 计算效率比较
在图3 电-气-热互联网络中,逐一增加耦合元件数量,从1 个耦合元件逐渐增加到4 个耦合元件。耦合元件数量越多,意味着IES 中的耦合越来越紧密。在每个耦合场景中,测量配置均为全量测,在有坏数据情况下利用基于GM 估计的集中式估计和本文所提分解协调鲁棒SE 方法分别进行计算。随着耦合元件的逐一增加,计算时间对比分别如图4 所示。
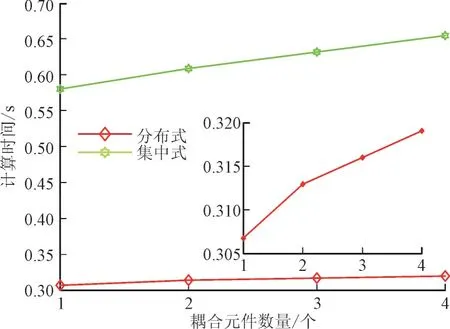
图4 有坏数据时计算时间对比图Fig.4 Comparison of computing time with bad data
由图4 可知,随着耦合元件的增多,网络的互联越来越紧密,对于集中式鲁棒SE 方法而言,耦合元件数量的增加导致雅可比矩阵的维数扩大甚至可能导致数值问题,因而估计时间将显著增加。对于本文所提方法,为了满足所有耦合元件边界约束的全局收敛,因而也需要更多的时间进行协调计算。但显然,在各种耦合条件下,本文所提分布式分解协调SE 方法估计时间更短,在计算效率上更有优势。
5 结语
本文针对IES 系统中电、气、热各子系统完备的实时网络数据不可共享问题,提出基于GM 估计的电-气-热IES 分解协调鲁棒SE 方法。基于电-气-热IES 系统典型结构进行仿真,仿真结果证实了本文所提分解协调SE 方法的有效性,可在电、气、热各个子系统要求商业隐私和保密性情况下,有效地进行各个系统的状态估计,并显著提高计算效率。

