高比例光伏和电动汽车接入配电网的无功优化

佟 曦，侯朗博，孙 昊，陈 衡，刘 涛，刘文毅

（1.华北电力大学，北京 102206；2.北京国电通网络技术有限公司，北京 100086）

0 引言

2020 年9 月，中国明确提出2030 年“碳达峰”和2060 年“碳中和”的目标。在这种背景下，分布式能源（Distributed Generation，DG）、分布式储能（Distributed Energy Storage，DS）和电动汽车（Electric Vehicle，EV）并入配电网逐渐在未来的电力行业占据重要位置，其渗透率也在逐步提高。高比例光伏和数量庞大的电动汽车接入电力网络，势必会对配电网的负荷、控制难度和用电质量等产生影响[1-3]，尤其是对电压和有功网损产生巨大影响。因此，需要对多种负荷接入的含高比例光伏和电动汽车的配电网进行研究和优化。

目前，国内外许多学者对新能源接入配电网后如何协调运行进行了深入的研究。文献[4-5]以无功补偿装置作为优化变量，利用场景分析法、凸松弛技术等进行无功优化研究，最后通过仿真算例验证了模型的精确性和可靠性；文献[6-8]提出了配电网多目标重构的方案，可以有效提高配电网的运行经济性；文献[9]根据分布式电源无功出力和电动汽车充电调度在不同时段相应提出相应的无功电压协调优化方案。

配电网无功优化问题，主要通过智能优化算法来实现。优化算法主要有遗传算法（Genetic Algorithm，GA）、粒子群算法（Particle Swarm Optimization，PSO）、禁忌算法（Tabu Search，TS）等[10]，其中PSO 算法因其寻优能力强，迭代次数少，耗时短而被广泛使用。文献[11]建立了含风电的无功优化模型，有效降低了配电网的网损，同时节点电压也得到了提升；文献[12]和文献[13]分别利用改进的量子粒子群算法以及混合型粒子群算法对含分布式电源的电力系统进行配电网重构研究；文献[14]研究了含分布式能源的配电网无功优化，建立了含DG 的无功优化模型，选取不同的实例进行仿真，结果验证了PSO 算法寻优能力强，收敛速度快。

影响光伏出力的主要因素是光照强度，其次，不同季节光照时间和温度高低也会对光伏出力产生影响[15-16]，因此光伏出力具有不确定性。此外，电动汽车充电也具有时序性，文献[17]研究表明私家电动汽车充电时间都集中在17—19 时之间，并且由于大多数电动汽车用来上下班，一辆车平均每天的行驶路程大致为42 km。

静止无功补偿装置（Static Var Compensator，SVC）由晶闸管控制电抗器和固定电容器组组成，通过调节晶闸管控制电抗器中的触发延迟角来连续调节补偿装置的无功功率；静止无功发生器（Static Var Generator，SVG）由于没有大量使用电容器，而是采用桥式变流电路多电平技术来进行处理，所以不需要使用时对系统中的阻抗进行计算。相较于SVC，SVG 具有体积小、能更加快速的连续动态平滑的调节无功功率的优点。

本文针对光伏出力的不确定性和电动汽车充电的时序性，以最小电压偏差和最小网络有功损耗为目标函数，建立了含光伏发电系统、电动汽车、储能系统和无功补偿装置（SVG）的配电网数学模型进行无功优化研究，并采用粒子群算法进行求解，最后通过IEEE30 节点系统验证了模型的有效性。

1 负荷数学模型

1.1 光伏出力特性

并网光伏发电系统主要由光伏阵列、逆变器和其他并网环节组成[18-19]，光伏阵列由光伏电池串联或并联组成，产生的电能通过逆变器和滤波器输入到电网。

1）太阳能板光照强度

光伏发电具有随机性，对光伏发电系统的输出功率有直接影响的参数有太阳辐射量，光伏发电系统受光面积等[20]。光照强度S的数学模型为：

式中：Sn1为直接辐射量；Sd1为散射辐射量；α为太阳高度角；θ为太阳能板与地面的夹角；n为地表反射率，通常取0.2。

2）光伏电池U-I特性分析

光伏电池的发电原理是光生伏打效应，光伏电池具有类似于二极管的结构，当光照射在电池上，会有电压产生。单独的光伏电池功率很小，所以要将大量的光伏电池串并联，以构成光伏发电系统。简化后的等效的光伏发电系统的U-I模型为：

式中：I和U为光伏发电系统的电流和电压；Idl为短路电流；Ukl为开路电压；Im为最大功率点电流；Um为最大功率点电压。

3）光伏功率特性分析

在实际投入使用中，由于环境因素的改变，实际的电压和电流会产生变化，需要对其进行修正。修正后的电压和电流为：

式中：Ud为修正后的电压；Id为修正后的电流；T为该时刻环境温度；Tst为标准电池温度，其值为25 ℃；Sst为标准光照强度，其值为1 000 MW/m2。

因此，光伏发电系统实际的有功功率为：

无功功率为QPV：

式中：φ为功率因数角。

1.2 电动汽车充电功率

1）行驶里程和荷电状态

电动汽车具有污染小、行驶成本低的特点，但由于电动汽车电池的能量密度相对较小，并且电池的性能易受到环境温度的影响，同时电动汽车的配套基础充电设施不够完善，使估算电动汽车的行驶里程具有不确定性[21-23]。根据数据研究表明，日行驶里程l近似服从正态分布，其概率函数为：

式中：μ为行程距离的期望值；μ=3.68；σ为标准差，拟合后取σ=0.88。

电动汽车的电池荷电状态（State of Charge，SOC）定义为剩余电量和最大电池容量的比值，日行驶里程的分布决定了起始SOC 的分布为：

式中：SOC,EV为电动汽车的电池荷电状态；L为电动汽车的满电状态下可行使的最大里程。

2）起始充电时间

采用对数正态分布来描述电动汽车最后一次出行结束时刻，即电动汽车开始充电时刻tc的概率密度函数：

3）充电功率

电动汽车充电时间的公式为：

式中：tcd为充电时长；Pc为充电功率；Q0为电动汽车电池容量。

充电功率的表达式为:

将电动汽车的耗电量和行驶距离看成线性关系，电动汽车每次充电需要的时间可以描述为：

式中：tm为电动汽车在完全充满电下的最大行驶时间。

在已知电动汽车起始充电时间和日行驶距离的前提下，通过式（14）参数转换后，可以推导出电动汽车每次充电所需时间的概率密度函数为：

式中：σD为标准差（无量纲）；σD=3.2；μD为期望值（无量纲），μD=17.8。

结合式（14）和式（15），可以得出充电功率为：

假设区域内电动汽车的电池特性相同，NEV,i为连接到负荷节点i上的数量，则汽车充电的总功率为：

为了保证电动汽车电池的使用寿命，要保证SOC 满足一定的约束要求，即：

1.3 储能系统充放电功率

储能系统的充放电过程实际上是与电网进行能量交互的过程，当储能电池进行充电时，储能电池通过双向变流器吸收配电网系统中其他元件所释放出的多余的电能；当储能电池进行放电时，通过双向变流器向电网释放多余的电能[24]。

1）剩余电量

蓄电池某一时间段的剩余电量为：

式中：St为t时刻剩余电量；St-1为t-1 时刻的剩余电量；κ为蓄电池自放电率；Uc,t-1，Uf,t-1分别为t-1时刻的充放电电压；Pc,t-1，Pf,t-1分别为t-1 时刻的充放电功率；ηc和ηf分别为充电效率和放电效率；tcn为充放电持续时间；QN为储能系统的容量。

2）电池荷电状态

蓄电池的荷电状态可表示为剩余电量与自身额定电量之比，即：

式中：SN为储能系统自身额定电量。

考虑到储能系统的寿命问题，在储能系统的充放电过程中，储能系统的SOC 状态不能超过设定的上下限，即：

2 无功优化模型

无功优化主要是通过添加或调整无功补偿装置来优化电力系统的运行状态，以达到改善电压质量、降低系统网损的目的[25]。其数学模型包括目标函数和约束函数，一般表达式为：

3 个表达式分别为目标函数、等式约束及不等式约束条件；u和x分别为控制变量和状态变量。

2.1 目标函数

本文从经济性和安全性角度出发，以系统有功网损Ploss和电压偏移量ΔU为目标函数，即：

式中：Gk(i,j)为节点i，j之间的电导；Ui，Uj为节点i，j的电压幅值；θij为节点i，j之间的电压相角差；n为支路总数；Uis为节点i的实际电压；UN为节点i的额定电压；Ui,max，Ui,min分别为节点i的电压上限值和下限值；N为节点总数。

多目标函数为：

式中：μ1，μ2为权重系数，μ1+μ2=1，0 ≤μ1≤1，0 ≤μ2≤1；本文取μ1=μ2=0.5。

2.2 约束函数

1）潮流平衡方程

在配电网系统无功优化中，等式约束也被称为潮流约束方程。光伏发电系统输出功率具有不确定性，储能系统和电动汽车在在不同控制条件下其充放电功率也具有不确定性，在任何状态下都需要满足潮流约束方程。

式中：PGi和PDi分别为节点i处输入和输出的有功功率；QGi和QDi分别为节点i处输入和输出的无功功率；QCi为节点i处的无功补偿量；Bij为支路i-j的电纳。

2）不等式约束

不等式约束条件包括节点电压约束、光伏发电系统的无功功率约束、电动汽车充电功率约束、储能系统的充放电功率约束以及无功补偿装置的无功功率约束，即：

式中：QPVi，PEVi，PDSi，QSVGi分别为节点i的光伏发电系统的有功功率，电动汽车的充电功率，储能装置的充放电功率，无功补偿器的无功功率；下标“min”和“max”分别表示对应参数的下限值和上限值。

3 仿真计算

3.1 算法介绍

PSO 算法是通过模拟鸟群觅食的行为方式创立的一种以群体协作为基础的随机搜索算法。假设算法中由M个粒子组成粒子群，飞行空间维数为D，粒子种群中第k个粒子的空间位置为xk，速度为vk，通过适应度函数计算自己适应度的值。其算法的更新迭代表达式为：

式中：k=1，2，3……，M；d=1，2，3，……，D，D为空间维数；t为迭代次数；ω为惯性权重；c1，c2为学习因子；r1，r2为随机变量，取值在（0，1）之间；v为粒子速度；x为粒子位置；pbt为第k个粒子的最优位置。

基于粒子群算法的无功优化问题流程见图1。

3.2 算例介绍

图2 为IEEE30 节点系统接线图，接入4组光伏发电系统（PV）、1组储能装置（DS）、电动汽车（EV）50 台和2组无功补偿装置（SVG），并网节点和接入节点容量见表1；图3—图5 分别为夏季某一天内的光伏太阳能板光照总强度、电动汽车预测负荷和储能装置充放电功率。

表1 负荷容量和接入节点Table 1 Load capacity and integrating node

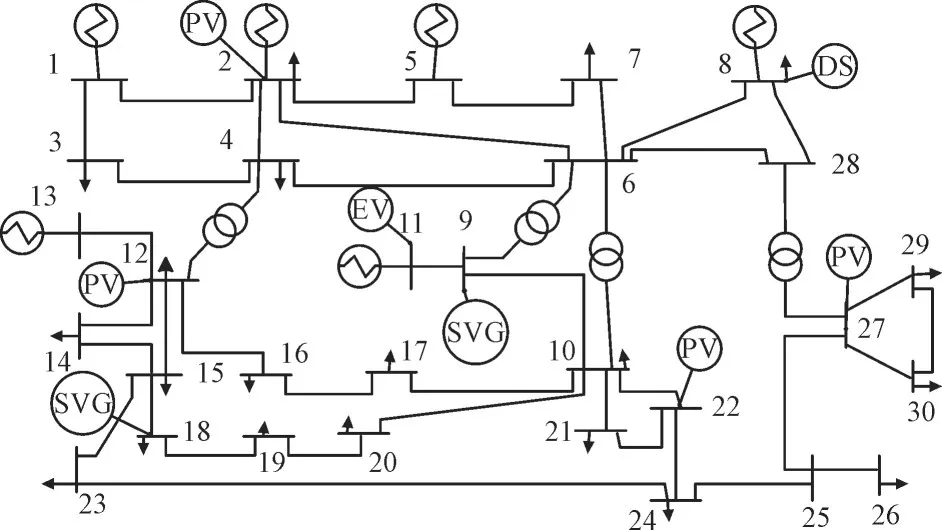
图2 IEEE30节点系统接线图Fig.2 Wiring diagram for IEEE30-node system

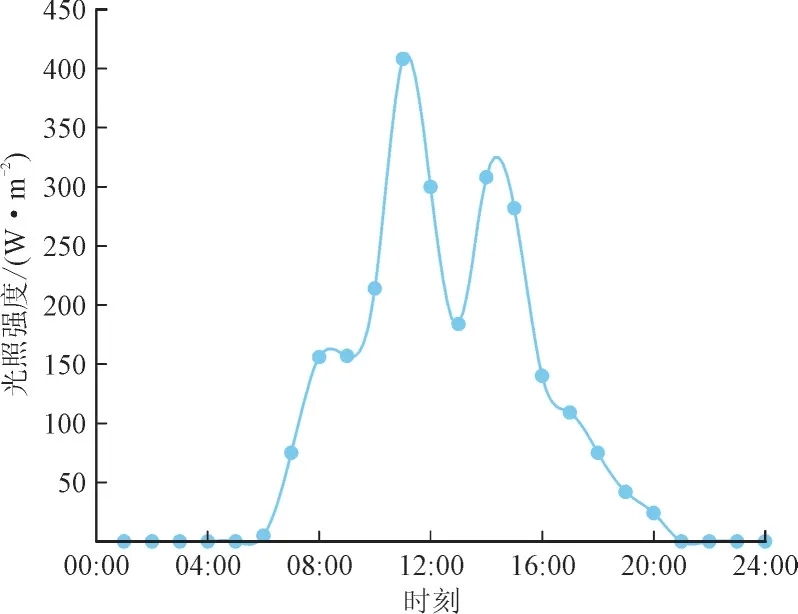
图3 光伏太阳能板光照强度Fig.3 Illumination intensity of photovoltaic solar panel

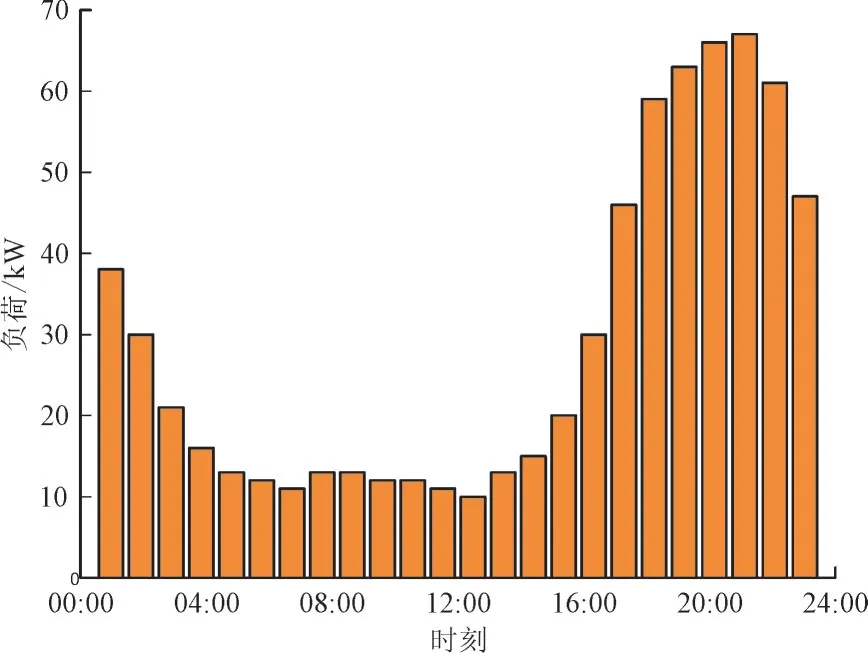
图4 电动汽车预测负荷Fig.4 Predicted load of EV

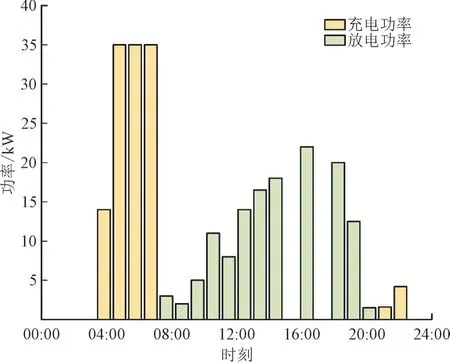
图5 储能装置充放电功率Fig.5 Charging and discharging power of energy storage system

3.3 结果分析

应用PSO 算法对本章问题进行计算寻优，设置种群最大迭代次数为100。结合MATLAB 中的matpower 进行潮流计算，利用粒子群算法进行无功优化运算后得到配电网中无功补偿装置在运行中的投切组数、有功网损和电压的优化情况。各时段投切电容器组数如表2 所示，24 h 内各时刻无功优化前后的网损情况如图6 所示。经计算，优化前总网损为141.91 MW，无功优化后的总网损为122.63 MW，在24 h 的优化时段内，将减少19.28 MW的有功功率的损失，总优化率达到13.58%。

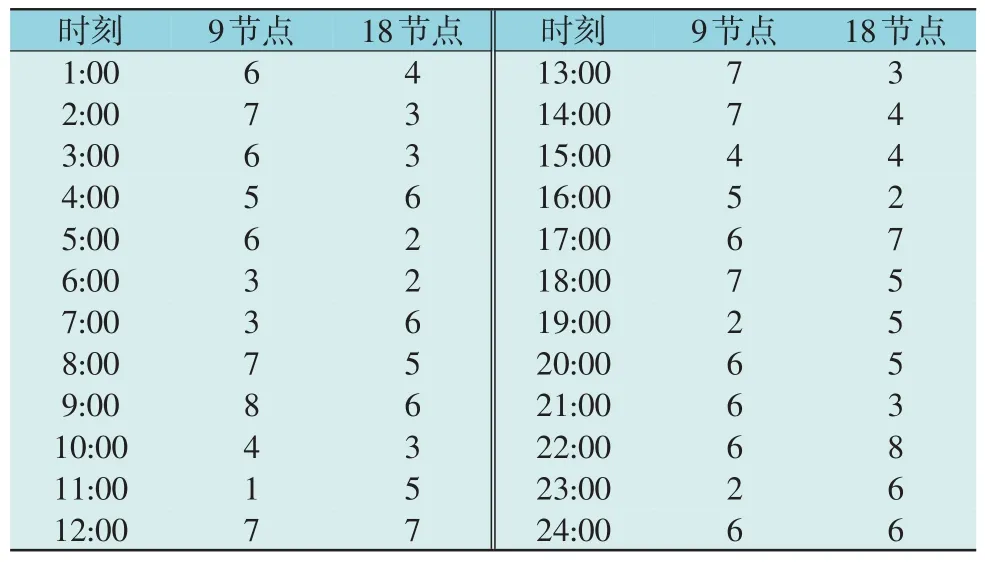
表2 各时刻投切电容器组数Table 2 The number of switching capacitor banks at each time

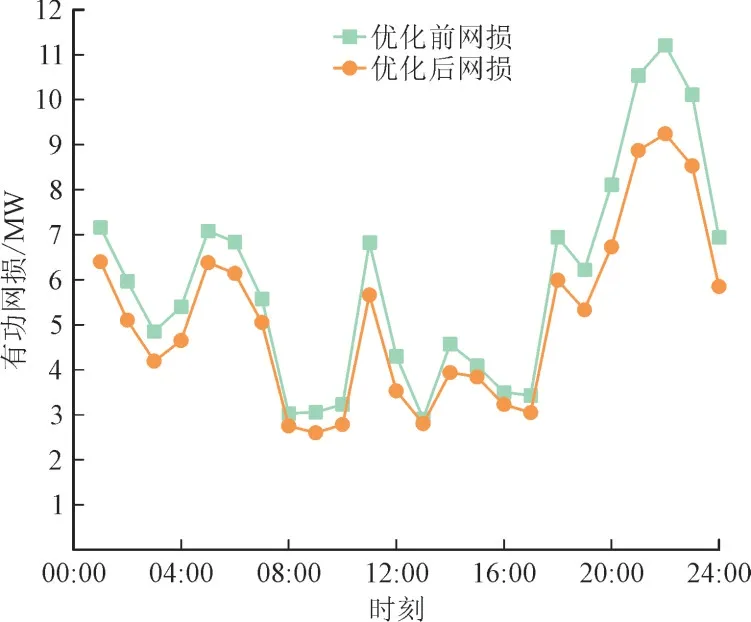
图6 优化前后网损对比图Fig.6 Comparison of network loss before and after optimization

为验证相较于传统SVG 接入方案的优势，同样选取9 节点和18 节点，固定投4 组电容器进行对比，再与所提方法进行比较，系统中分时段优化对比效果如图7。

图7 不同接入方案下网损对比图Fig.7 Comparison of network loss under different integration schemes

图7 中蓝色折线表示固定投入电容器组数优化后24 h 内配电网有功网损情况；橙色曲线表示在利用优化算法计算后的投入电容器组数优化后24 h内配电网有功网损情况。传统接入方案下，其总网损为135.32 MW，相较于不加入无功补偿装置的总网损，降低了6.59 MW，总优化率为4.64%；而使用本文所提出的使用优化算法计算电容器组数的方法，总网损降低了19.28 MW。相较于传统方案，其总网损降低12.69 MW，系统优化率提高了8.94%，验证了本文所提出利用智能算法计算电容器组数从而降低网损的优势。

选取其中网损最大的22 时刻，其优化前后节点电压和优化算法结果如图8 和图9。

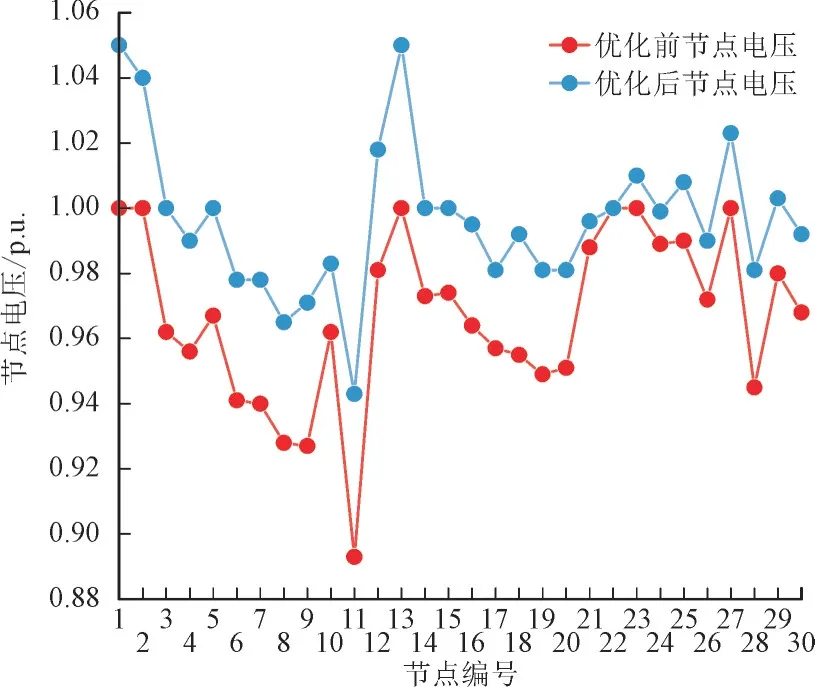
图8 22时优化前后节点电压图Fig.8 Diagram showing node voltage before and after optimization at 22:00

图9 PSO优化算法结果Fig.9 Results of PSO algorithm

通过分析可知，优化前节点电压在0.89 p.u.～1.00 p.u.之间，优化后全时间段电压0.94 p.u.～1.05 p.u.之间，属于正常限度内，电压波动较优化前趋于平缓，减小了用户负载以及生产生活受到光伏发电设备和电动汽车以及储能装置接入配电网带来的功率波动干扰。图9 的PSO 优化算法在迭代43 次后趋于稳定，证明算法寻优能力强，收敛速度快。

4 结论

针对光伏出力的不确定性和电动汽车充电时序性，构建了包含光伏发电系统和电动汽车充电的数学模型，并且根据模型和数据绘制了光照强度以及电动汽车充电功率预测曲线图。将储能装置接入含高比例光伏和电动汽车的IEEE30 节点电力系统中，通过投切无功补偿装置电容器组数来进行系统的无功调节，得出如下结论：

1）高比例光伏和电动汽车接入电网，给电网带巨大影响，接入SVG 补偿器进行无功补偿，能够有效地降低光伏和电动汽车接入后的有功网络损耗。

2）粒子群优化算法求解无功补偿装置SVG 投切电容器组数的方案相较于传统投入固定SVG 投切电容器组数的方案，其网损更小，优化率更高，验证了本文所提出利用智能算法计算电容器组数从而降低网损的优势。

3）本文所提利用粒子群优化算法求解无功补偿装置SVG 投切电容器组数的方案，在优化后全时间段电压均在0.94 p.u.～1.05 p.u.之间，属于正常限度内，电压波动较优化前趋于平缓，证明使用该寻优方法优化后可以保证节点电压的稳定性。