基于功率轨迹预设的双馈风电机组虚拟惯量控制策略

林 旭，李 军，杨德健，王 鑫，王汝田，金朝阳

（1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林吉林 132012；2.电网智能化调度与控制教育部重点实验室（山东大学），山东济南 250061）

0 引言

截至2022 年11 月底，2022 年1—11 月份全国发电装机容量约2.51×109kW，同比增长8.1%，其中风电装机容量约3.5×108kW，同比增长15.1%，为推动达成碳达峰、碳中和战略目标的实现，预计未来几年我国的风电装机容量将会持续快速增长[1]。双馈风力发电机（Doubly-fed Induction Generator，DFIG）是目前风电场的主流机型，其通过变流器实现转子侧与电网侧的功能交换，采用矢量控制技术，具有功率解耦控制、最大风能跟踪（Maximum Power Point Tracking，MPPT）等优点[2]，但不具备惯性响应能力[3]，在风机渗透率不断增加的情况下，电力系统的惯量和频率控制能力会显著下降[4]，恶化系统频率安全特性和制约风电消纳水平，当系统频率偏差过大会触发低频率减载等保护动作[5-7]，从而对整个系统的频率安全稳定性造成危害。

DFIG 参与调频控制策略主要有转子动能控制[8]和功率备用控制[9]，功率备用控制通过变桨控制、超速控制留出备用，支撑系统调频。其中变桨控制通过控制风机桨距角降低有功出力，但频繁切换桨距角会增加风机磨损[10-12]，超速控制受风机转速的制约只适用于风速较低的情况下[13]；转子动能控制利用风机转子释放动能参与系统调频[14]，其主要包括：惯性控制[15]、下垂控制[16]及功率轨迹预设控制策略[17]，惯性控制与下垂控制以测量频率信息为输入，经控制回路调整自身出力，通过释放转子中的动能补偿系统功率缺额[18-19]；功率轨迹预设控制策略在检测到扰动后，瞬时增加风机有功出力，响应速度快，避免因频率测量误差造成的调频不当甚至是失稳问题[20-21]。

功率预设轨迹方法是提供系统频率支撑的设计风机有功出力曲线。然而，如何更好地发挥风机的调频能力仍需深入研究。文献[22]中考虑DFIG转矩极限值设计有功出力曲线，虽减少了二次频率跌落，但转速恢复阶段DFIG 有功输出减小幅度小，且需要较长恢复时间。文献[23]提出短时功率支撑控制策略，DFIG 为调频提供短时功率支撑，具有可控性强的优点，但若恒定功率维持时间预设不当，可能过度释放转子动能导致失速风险，并引起频率二次跌落。文献[24]提出一种基于短时功率支撑控制策略的自适应功率参考函数，其随时间增大而减小，有效减小频率二次跌落，但功率支撑阶段该方法的有功输出快速下降会影响对系统频率最低点的支撑作用。

综上分析，本文提出基于功率轨迹预设的虚拟惯量控制方法，该方法首先提供与传统虚拟惯量控制策略相同的恒定功率支撑，而后基于系统频率最低点产生时间，设定频率支撑时间，旨在维持调频能力的同时释放更少转子动能。转速恢复阶段，通过建立有功出力随时间变化的线性函数，在设定的时间内，有功出力缓慢恢复至最大功率跟踪曲线，实现可控的转速恢复周期及减小频率的二次跌落的目标，最后通过仿真分析验证在不同变风速场景下改进方法的有效性。

1 DFIG的惯性响应机理分析

DFIG 主要由风力机，齿轮箱，双馈感应电机及电力电子装置构成，如图1 所示。DFIG 通过变流器多环路控制决定交流电压相位与幅值，实现最大功率跟踪等高级控制策略。图1 中，vw为风速，β为桨距角，PM为风机捕获机械功率，ωr为转子转速，Vs和Is分别为定子侧电压和电流，Vr和Ir分别为转子侧电压和电流，Vd为直流电压，输入网侧变流器维持Vd值恒定，Qr和Qs分别为转子侧及定子侧无功功率参考值。

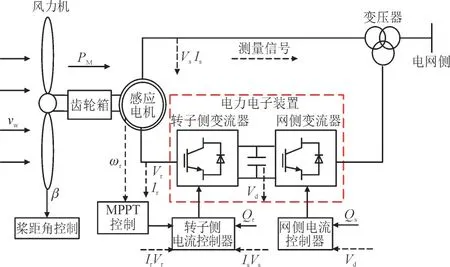
图1 DFIG典型配置及控制系统图Fig.1 Typcial configuration and control system of DFIG

DFIG 捕获机械功率PM如式（1）所示:

式中：ρ为空气密度；rw为风机叶片半径；Cp为风能利用系数，是叶尖速比λ和桨距角β的非线性函数。

叶尖速比λ为风机叶片尖端线速度与风速之比，如式（2）所示：

式中：ωw为风力机叶片角速度。

当β为0，风能利用系数达到最大，DFIG 通过控制转子转速ωr实现最大风能捕获，进而实现MPPT 运行模式如式（3）所示：

式中：PMPPT为最大功率跟踪曲线；CPmax为最大风能利用系数；λ0为最优叶尖速比。

DFIG 的惯性响应表现为系统频率变化的缓冲能力，当系统发生频率扰动时，DFIG 释放转子中储存的动能，增大电磁功率，降低转速，其动态过程如式（4）所示[18]：

式中：HDFIG为DFIG 惯性时间常数；ωpu为转子角速度标幺值；ΔPpu为扰动的标幺值；t为时间。

由于标幺值系统中的系统频率fpu与ωpu相同[22]，对式（4）积分，得出tr至td时刻DFIG 释放动能与频率变化关系如式（5）所示：

式中：tr为扰动初始时刻；td为系统频率跌落最低点时刻；ΔEpu为DFIG 释放动能的标幺值；Δf(td-tr).pu为tr时刻至td时刻的系统频率变化。

进一步化简式（5）可得：

根据式（6）得出，在tr至td时刻DFIG 转子释放动能ΔEpu增大，td时刻的系统频率会随之增加，即当系统频率下降时，DFIG 参与调频释放转子旋转动能增加有功输出，可提高频率最低点，抑制频率波动。

2 DFIG虚拟惯性控制策略

2.1 传统控制策略

文献[23]提出了基于功率轨迹预设的风电机组虚拟惯量控制方法，扰动发生后风电机组切换至惯量控制模式，如图2 所示。其中，ΔP为频率支撑阶段恒定的有功增量，Pref1为传统控制策略的有功出力，P0为扰动前测得的恒定PMPPT值，t0，t1，t2为风机在传统策略下的运行时间点。

图2 传统控制策略框图Fig.2 Diagram showing traditional control strategy

按照有功功率预设轨迹提供调节风机有功输出，有功参考值曲线如图3 所示，包括频率支撑阶段和转速恢复阶段，其中，A，B，C，D，E为风机有功运行点。

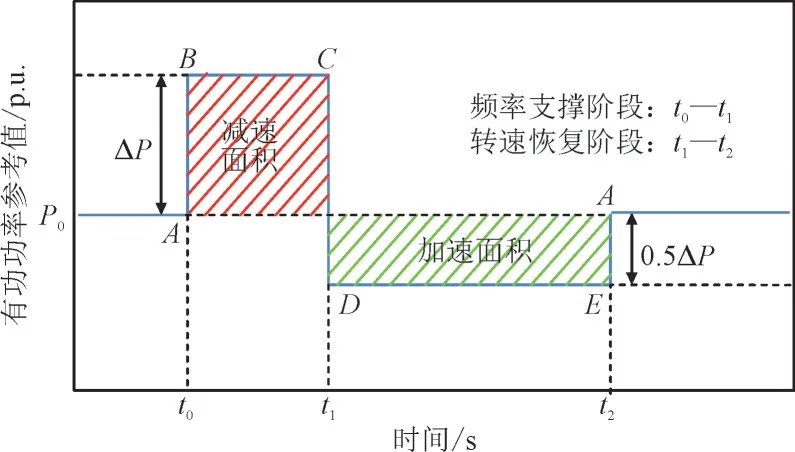
图3 传统控制策略原理图Fig.3 Schematic diagram of traditional control strategy

频率支撑阶段，风机有功出力从P0增加至P0+ΔP，维持t0→t1时段，文中t0→t1时段设为10 s，风机转子释放旋转动能，提升频率最低点。该阶段风机有功运行点由A点垂直升至B点，并维持至C点。转速恢复阶段，风机有功出力瞬间从P0+ΔP的状态切换并维持t1→t2时段的P0-0.5ΔP状态，文中t1→t2时段设置为20 s，此时风机有功运行点由C点垂直下降到D点，并平移至E点，风机输出的电磁功率小于输入的机械功率，风机转子吸收能量，转速逐渐增大，为确保风机转速恢复至初始状态，需要满足加速面积等于减速面积，即频率支撑阶段风机释放转子动能等于转速恢复阶段风机吸收储存的动能。

然而，文献[23]提出的虚拟惯量控制策略存在以下问题：

1）系统受扰动后，频率最低点大约在3～5 s 后产生[25-26]，恒定ΔP维持时间过长，风机转子动能过度释放，可能会造成转速过低而产生失速风险。

2）转速恢复阶段，有功出力瞬间切换状态系统会再次感受到扰动造成二次频率跌落，严重时会低于频率跌落最低点，特别是在变动风速场景下，容易诱发风机失速，进一步恶化系统的频率动态响应特性。

2.2 改进控制策略

针对传统控制策略存在问题，本文提出改进虚拟惯量控制策略，通过设置合理的ΔP维持时间减小转子动能释放，兼顾频率跌落最低点支撑，并优化了频率二次跌落问题，功率预设轨迹如图4 所示，其中ta，tb，tc，td，te为风机在改进策略下的运行时间点，ΔPC为有功运行点C所对应的有功增量。

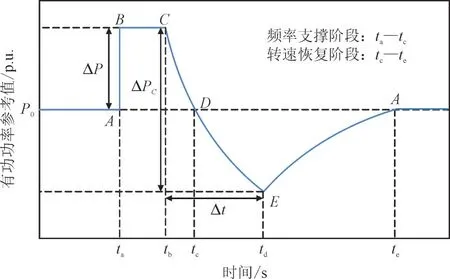
图4 改进控制策略原理图Fig.4 Schematic diagram of improved control strategy

在频率支撑阶段，由于系统频率跌落最低点大约出现在扰动后3～5 s，为保证频率支撑效果并减小转子动能过度释放，减小风机失速的风险，在风机频率支撑阶段有功增量ΔP保持大小不变前提下，将维持时间缩减为ta→tb，文中设置ta→tb时段为5 s。此阶段风机有功运行点由A点垂直上升至B点，并平移到C点，风机有功参考值大小如式（7）所示，其中ΔP的值与传统方法一致：

式中：Pref2为改进控制策略的有功出力。

为使转子恢复转速，风机输入的电磁功率应小于输出的机械功率，传统控制策略瞬时改变有功出力将会造成严重的频率二次跌落。因此，本文在tb→td时段建立Pref2随时间增大而减小的线性函数以减缓跌落速度如式（8）所示。此阶段风机有功运行点由C点运行到E点，有功运行D对应tc时刻为风机转子开始恢复转速。

式中：Pm0为tb时测得的恒定PMPPT值；Δt为tb→td时段时间变化量。

Δt决定了二次频率跌落程度及转速的恢复速度，其值较小会产生显著的二次频率跌落，其值较大会使转速的恢复速度相对较慢。因此，为在系统二次频率控制启动前恢复至MPPT 运行（扰动后20～30 s 启动二次频率跌落），本文设置Δt=15 s。

当ΔPC随时间缩减为0 时，DFIG 的有功出力如式（10）所示：

在td→te时段，风机有功运行点由E点收敛到A点，Pref2恢复至PMPPT状态，风机逐渐恢复到扰动前状态。

针对传统虚拟惯量控制策略存在问题，进行了以下改进：

1）频率支撑阶段，风机缩减恒定有功出力维持时间，减小转子动能释放，兼顾频率跌落最低点支撑，合理调用风机惯性调频潜力，减小产生失速风险。

2）在转速恢复阶段，确立有功参考值随时间增大而减小的线性关系，改进基于有功参考值瞬时减小的控制方式，以有效减小有功出力瞬间跌落引起的频率二次跌落。当ΔPC缩减为0 时，功率轨迹将返回MPPT 曲线，使风机平稳退出调频，避免对系统频率的二次冲击。

3 仿真分析

为验证本文改进策略有效性，基于仿真平台EMTP-RV 建立含风电的IEEE 14 系统，如图5 所示。其中1—14 为母线节点，G1—G5为同步发电机，装机容量分别为615 MW，130 MW，120 MW，120MW，60MW，L2—L14为系统静态负载，总计539MW。

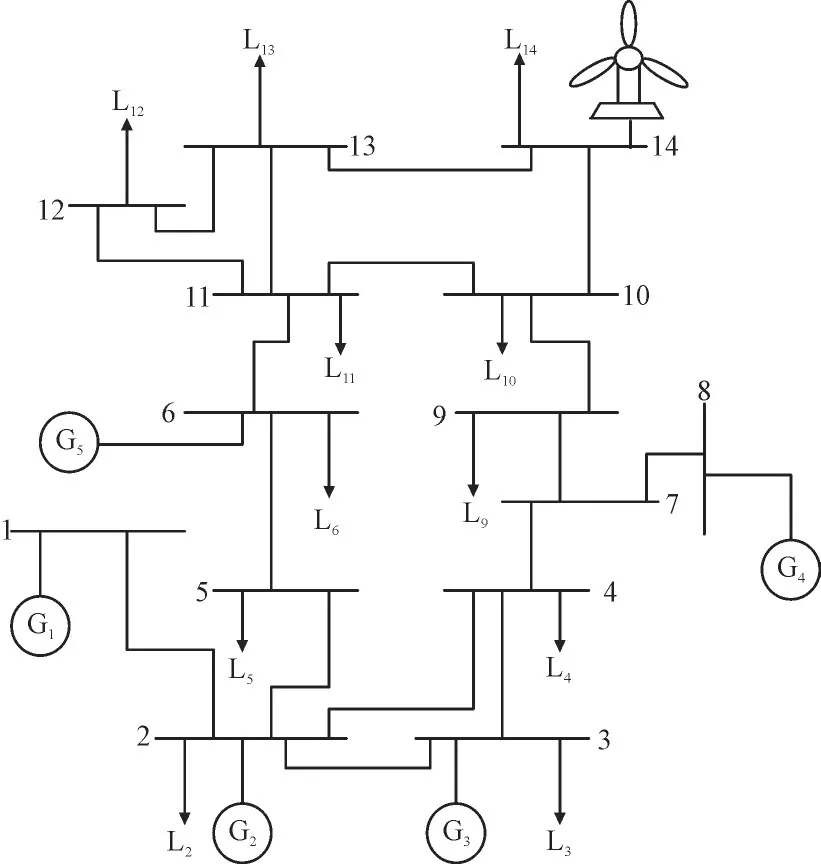
图5 仿真系统模型Fig.5 Model of simulation system

在仿真过程中，参考魁北克电网导则[16]设置ΔP为0.1 p.u.，为更加贴切现实风机运行情况，设置t=50 s 同步机G2脱网产生100 MW 功率缺额后，选取2 种随机波动风速场景（在50 s 扰动前DFIG 进行初始化，风速需保持恒定），如图6 所示。

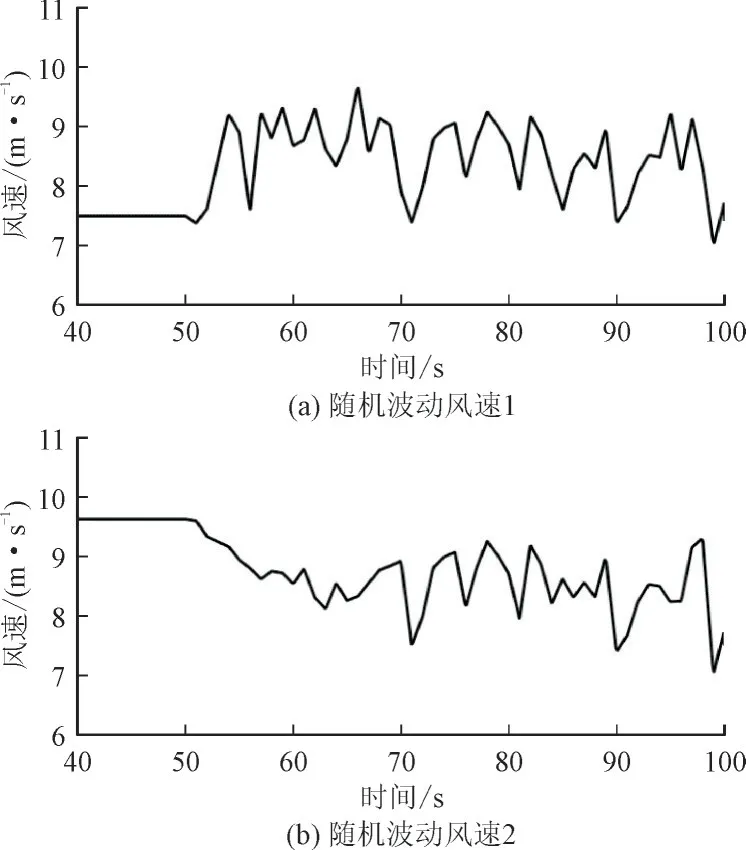
图6 变风速场景Fig.6 Scenario of variable wind speed

由图6 可知，随机波动风速1 与随机波动风速2 初期（频率支撑阶段）相较于初始风速具有整体增加与降低的变化特征。通过对运行在MPPT、传统策略、改进策略下的风机自身稳定性及调频结果，验证改进策略在变风速情况下的有效性。

1）算例1：变风速场景1。算例1 仿真结果如图7 所示。

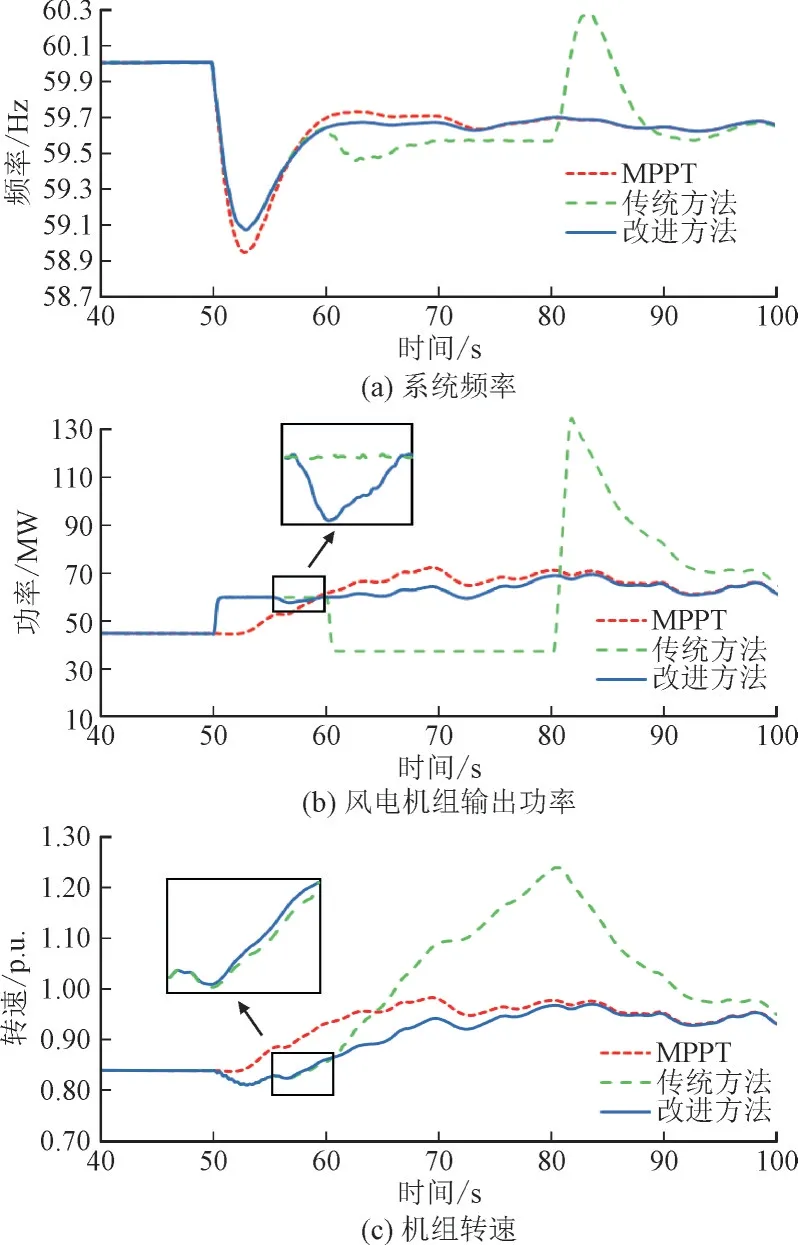
图7 算例1仿真结果Fig.7 Simulation results of case 1

在t=50 s 时同步机G2脱机造成100 MW 扰动，此时系统频率开始下降触发风机参与调频。在频率支撑阶段，当风机在MPPT 运行模式下不参与调频，系统频率最低点下降为58.952 Hz；当DFIG 分别以传统策略和改进策略运行时，采用改进方法和传统方法的风机有功输出迅速增加15 MW，系统频率最低点由58.952 Hz 提升到59.086 Hz，频率最低点提高了0.116 Hz。

在转速恢复阶段，传统策略下有功增量瞬间改变为-0.5ΔP的状态，造成了新的有功冲击，系统出现0.184 Hz 的二次频率跌落，80 s 时控制信号触发风机恢复至MPPT 模式，但此时由于风速的波动导致风机80 s 时的转速值区别于扰动前状态的转速值，经过20 s 暂态过程后风机逐步恢复至初始状态，期间产生超调现象；改进方法通过预设有功出力轨迹随时间逐步改变至MPPT 模式，90 s 左右，风机能够根据风速变化的特点平稳地改变至MPPT 模式后退出调频，消除频率二次跌落。

2）算例2：变风速场景2。算例2 仿真结果如图8 所示。在频率支撑阶段，当发生扰动后采用MPPT控制策略时，系统频率最低点为58.952 Hz。DFIG在传统方法和改进方法控制策略下功率预设轨迹与算例1 相同，频率跌落最低点提升至59.086 Hz。

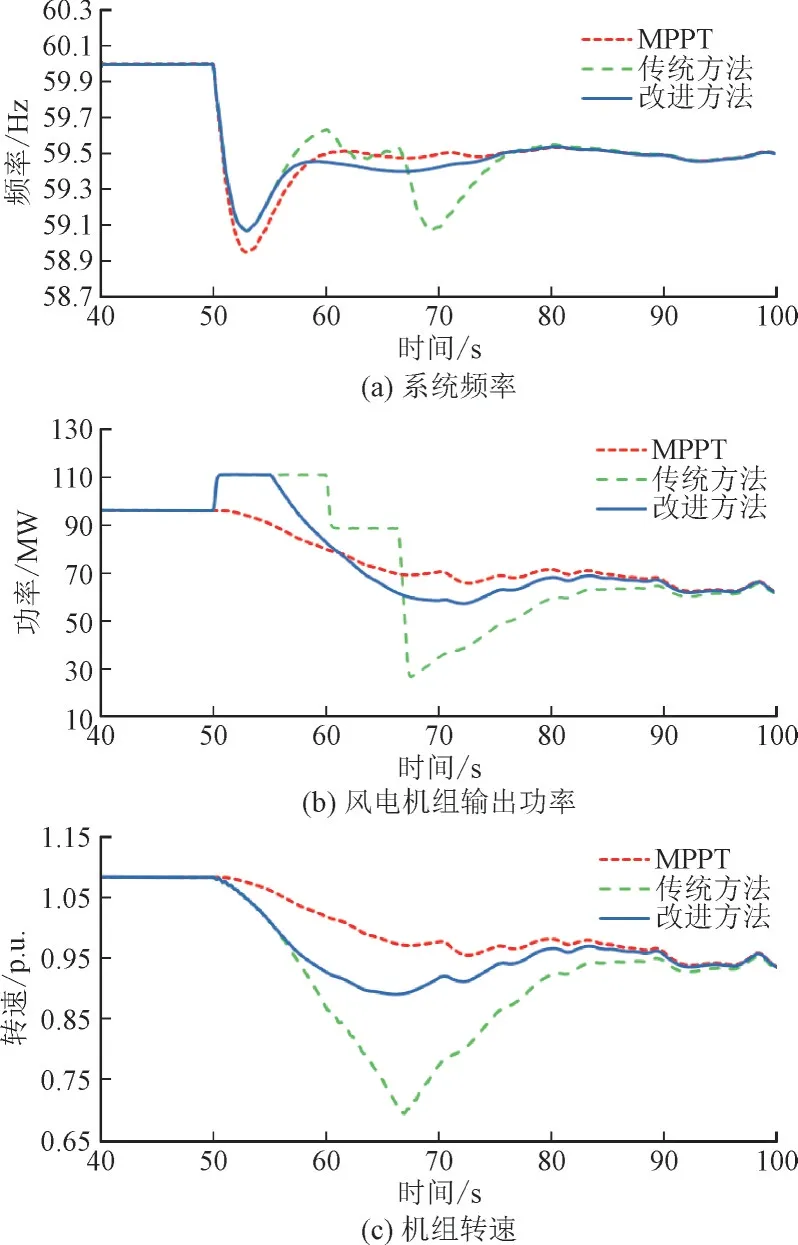
图8 算例2仿真结果Fig.8 Simulation results of case 2

在转速恢复阶段，传统策略下有功预设轨迹为恢复转速瞬间切换状态，引发了0.161 Hz 的二次频率跌落，并且由于风速的急剧下降，此时风机的转速会继续下降，诱发失速风险，严重影响风机自身运行稳定性，70 s 时再次造成了0.461 Hz 的频率跌落；改进策略下机组转速在变风速场景2 的下降程度小于传统策略，如图8（c）所示，验证了改进方法可以减少风机的转子动能释放，避免了在波动风速下转子动能过度释放造成的失速现象，从而削弱由于风机的自身稳定性问题对系统频率的影响。

4 结论

针对传统虚拟惯量控制策略存在问题，本文提出一种改进控制策略，提升DFIG 频率调节能力，有效改善转速失速及二次频率跌落问题。通过仿真分析得到如下结论：

1）频率支撑阶段，改进控制策略在有效满足支撑频率的同时，减少动能释放，充分利用风机调频潜质，避免风机转子动能过度释放，减少不必要的转子动能释放。

2）转速恢复阶段，传统控制策略在有功出力瞬间切换状态，并在波动风速下因转子动能过度释放造成的失速现象，诱发了严重的频率二次跌落，改进策略通过预设功率轨迹随时间逐步改变至MPPT模式，避免了在波动风速下转子动能过度释放造成的失速现象，减小风机因自身稳定性问题对系统频率的冲击。