基于光伏-MGP并网系统的控制参数整定方法

王 岳，李晨阳，黄永章，张馨月，王 童，赵海森

（1.新能源电力系统国家重点实验室（华北电力大学），北京 102206）；2.国网南京市供电公司，江苏南京 210000）

0 引言

近年来，新能源发电在国民经济与生活中发挥日益重要的作用。新能源的大规模接入使电网呈现电力电子化特性，进而引发一系列的稳定性问题，如频率调节能力下降、电压稳定问题突出等[1-2]。

根据控制对象的不同，并网逆变器的控制主要分为电流源模式和电压源模式。电流源模式的并网逆变器主要采用基于锁相环（Phase-Locked Loop，PLL）控制的电压定向方案[3-4]。在强电网下具有较强的稳定性，但在电网阻抗波动时，电流源模式逆变器的稳定裕度会下降[5]。针对此问题，有学者提出了无需使用PLL 的电压源模式并网逆变器控制策略[6-7]，但该控制在系统大扰动时会出现机理更为复杂的同步暂态失稳现象[8]。针对同步暂态失稳问题，有学者从控制环节、参数整定等角度对逆变器控制进行优化[9-13]，但仍然不能从根本上解决高占比电力电子逆变器对电网带来的弱阻尼和低惯量等稳定性问题。

为克服逆变器的不足，有学者提出了一种基于电动机-发电机对（Motor-Generator Pair，MGP）的并网新方式[14]，也称为新能源同步机。相比于传统新能源并网，新能源同步机具有多种优点[15-17]。文献[16]通过实验证明MGP 能显著抑制系统震荡，并能为新能源电力系统提供足够的惯性响应。文献[17]通过仿真研究证明，将MGP 集成到电网可以减小系统的频率变化率（Rate of Change of Frequency，RoCoF）约20%，降低光伏输出直流电流冲击约17%。

新能源采用MGP 并网首先要确保控制的稳定性，即对控制参数进行准确整定。然而目前国内外学者提出的参数整定方法均针对于电力电子变流器[18-22]，由于MGP 在并网环节与常规新能源并网存在较大差异，常规变流器控制参数整定方法无法直接用于新能源-MGP 并网系统，因此亟需研究适用于MGP 系统的控制参数整定方法。

本文将从理论计算的角度对MGP 系统的控制参数进行整定。以光伏-MGP 并网系统为例，通过分析光伏采用直流电压反馈控制驱动MGP 的控制原理，建立适用于描述该系统动态特性的简化传递函数；基于频域内系统的幅值和相位裕度，以及系统单位阶跃响应中的超调量、峰值时间为衡量标准，确定控制系统的最优控制参数，最终形成用于光伏-MGP 并网控制参数整定的通用性方法。

1 光伏经MGP 并网的直流电压反馈控制

1.1 MGP并网结构

新能源采用MGP 并网的结构如图1 所示。光伏、风机等新能源电力通过变流器逆变为交流电，驱动同步电动机旋转，电动机拖动同步发电机并网。

图1 MGP系统结构图Fig.1 MGP system structure diagram

关于光伏经MGP 并网系统的效率、成本等方面，已有学者进行了研究[23-25]。文献[24]通过搭建新能源经MGP 并网实验平台，计算出MGP 并网系统运行效率约为90%。虽然该效率略低于光伏经逆变器并网，但MGP 并网系统具有更好的经济效益。文献[25]通过理论计算与仿真分析，得出50 MW 的新能源经MGP 并网系统的投资成本，是同容量、提供相同惯性的光伏经逆变器并网系统的1/10。因此将MGP 应用于光伏等新能源并网系统，较传统新能源并网方式具有更多优势。

1.2 MGP的功角特性及运动方程

MGP 系统由2 台同步机组成，MGP 的相位和电压矢量关系如图2 所示。

图2 MGP系统的电压矢量图Fig.2 Voltage vector diagram of MGP system

图2 中，UM和EM为电动机的端电压和内电势；U′M和E′M为变化后的电动机端电压和内电势；U0和E0为发电机的端电压和内电势，U0也代表并网点的电网电压；δM和δG为电动机与发电机的功角；δC为电动机和发电机内电势的夹角；Δθ为电动机和发电机端电压的夹角，称为MGP 系统的功角；Δθ′为电动机和发电机端电压相位变化后的夹角。

基于图2 的电压矢量关系，MGP 系统的功率传输方程可以表示为式（1）和式（2），功角关系可以表示为式（3）：

式中：PM为同步电动机的有功功率；PG为同步发电机的有功功率；XM为电动机定子同步电抗；XG为发电机定子同步电抗；Δδ为MGP 的功角变化量。

根据图2 并结合式（1）—式（3）可知，当以U0为电压相位参考时，UM相位的变化可以造成MGP 系统功角的变化，从而改变MGP 系统的功率传输，这就是MGP 系统的功角特性。由于MGP 系统由2台同步电机组成，根据单台同步电机的转子运动方程，可以得到MGP 系统的运动方程，如式（4）和式（5）所示：

式中：HM与HG为同步电动机和同步发电机的惯性时间常数；TeM与TeG为同步电动机和同步发电机的电磁转矩；KDM与KDG为同步电动机和同步发电机的阻尼系数；ω0为额定转速；Δωr为MGP 转子轴转速偏差量。

1.3 MGP的直流电压反馈控制

改变MGP 输出有功功率的关键，是改变图1中MGP 的源-网相位差Δθ，而控制Δθ的关键是改变UM的相位。为此，有学者提出了基于调频的MGP 功率反馈控制[22]。当MGP 并网时，U0的频率为50 Hz，通过控制逆变器调制波的频率，调节UM的相位，最终实现对MGP 输出有功功率的控制。

MGP 功率反馈控制的控制环节简单，但在光照强度、环境温度变化时，光伏端电压将会发生波动，MGP 将无法以恒定功率输出运行。为解决此问题，有学者提出了MGP 的直流电压反馈控制，简称MGP电压反馈控制。电压反馈控制的控制框图如图3 所示。

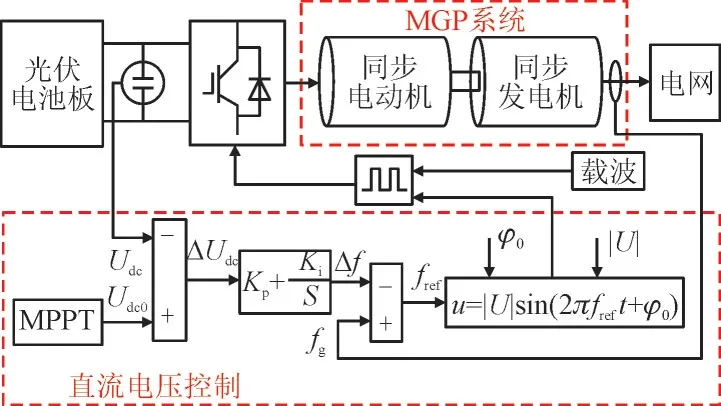
图3 MGP直流电压反馈控制Fig.3 DC voltage feedback control for MGP

图3 中，光伏最大功率点跟踪控制（Maximum Power Point Tracking，MPPT）提供光伏最大输出功率点对应的参考电压Udc0。根据光伏端电压与变频器传输功率的变化特性，可以制定MGP 直流电压反馈控制策略：对比光伏端电压Udc与Udc0，将偏差值ΔUdc乘比例系数Kp与积分系数Ki后，转化为频率修正量Δf，并对电网电压频率fg进行修正，得到变频器调制波的频率参考值fref，最终改变电动机端电压频率。调制波的电压幅值|U|与初始相位φ0为定值。由于发电机端电压的频率被电网钳位并稳定在额定值，电动机与发电机端电压的相位差会出现改变，可以实现对MGP 有功功率输出的控制，进而调节直流电容电压，改变光伏输出功率与Udc，实现Udc对Udc0的跟踪效果。

2 电压反馈并网控制系统参数整定方法

2.1 控制系统建模

为了进行控制系统的稳定性分析及参数整定，首先建立基于电压反馈的控制框图如图4 所示。

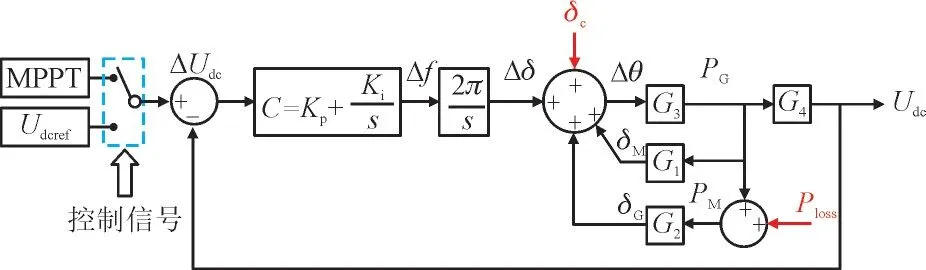
图4 MGP系统电压反馈控制系统框图Fig.4 Block diagram of voltage feedback control for MGP system

图4 中，G1，G2为发电机和电动机的功角-功率传递函数；G3为MGP 系统的功角-功率传递函数；G4为MGP 输出功率与光伏板端电压的传递函数；C为PI 控制器的传递函数；Ploss为MGP 系统的损耗；Udc为光伏端电压；Udcref为光伏端电压设定值；Kp为比例系数；Ki为积分系数；控制信号用来切换直流电压参考值的设定方式，由控制装置给出或手动选择。

2.1.1 传递函数G1，G2，G3

根据式（1）与式（2）可知，同步电机发出或吸收的有功功率P与功角δ呈正弦函数的关系，不易直接得出传递函数。由于功角曲线上局部功率与功角近似呈线性化关系，因此采用线性化与仿真/实验测量相结合的方式，近似构造出功率-功角的传递函数：

式中：kδ-G，kδ-M为同步电机功率-功角近似的线性关系系数；TG，TM分别为同步电动机和发电机的时间常数。

因为MGP 系统是由2 台参数相同的同步电机组成，故MGP 系统的特性可认为是2 台同步机特性的叠加。对于MGP 系统的功角-功率传递函数G3，其形式仍满足于：

式中：kδ-MGP为MGP 系统功率与功角近似的线性关系系数；TMGP为MGP 系统的时间常数。

2.1.2 传递函数G4

本文通过一种线性化的实用性等效方法，对该传递函数进行构造。MGP 系统在稳定运行时，光伏运行在最大功率点，输出的有功功率PMGP为定值，且光伏端电压Udc一般变化不大。因此在短时间尺度内PMGP与Udc的比值可近似计算为定值，即认为传递函数G4为常数。

2.1.3 传递函数CPI 控制器的传递函数为:

式中：Kp与Ki为比例系数与积分系数。

PI 控制器将光伏端电压偏差转化为对逆变器调制波的修正量，是直流电压反馈控制的关键环节。Kp与Ki参数的选取，将直接影响控制系统的控制效果与MGP 系统的动态响应性能。Kp与Ki的整定，是本文研究的重点。

2.2 控制系统参数的整定方法

完成直流电压反馈控制中控制环节与传递函数的构建后，将对各个传递函数中涉及的参数进行整定计算。

2.2.1 传递函数G1～G4中参数的整定

根据式（6）可知，传递函数G1中涉及同步发电机线性关系系数kδ-G和时间常数TG。

线性关系系数kδ-G可以通过线性化同步发电机功角-功率曲线进行整定：通过运行MGP 系统的仿真模型或样机平台，绘制出同步发电机的功率-功角曲线，将该曲线进行局部线性化并计算斜率，即可得到同步发电机的功率-功角线性关系系数kδ-G；时间常数TG即为同步发电机的惯性时间常数。

由于MGP 系统中电动机与发电机的参数完全相同，故传递函数G2中涉及的kδ-M，TM与同步发电机完全相同，即kδ-G=kδ-M，TG=TM。

由于MGP 系统的功角为发电机与电动机功角之和，同时其输出功率与发电机相同，故有：kδ-MGP=（kδ-M+kδ-G）/2。根据式（4）与式（5）中MGP 系统的运动方程可知：TMGP=TM+TG。

根据光伏输出有功功率与端电压的关系可知，当光伏端电压的设定值为Udc=Udc0时，光伏输出的有功功率为Pdc=Pdc0。由于MGP 系统的功率损耗为定值，设为P0。故此时G4可近似表示为：G4=Udc0/（Pdc0-P0）。

2.2.2 比例系数Kp的选取

在分析比例系数Kp的选取前，先确定能使系统稳定运行的Kp的范围。首先忽略积分系数Ki，即令Ki=0，C=Kp。由于初始转子角和功率损耗基本固定，在分析Kp对系统的影响时，可以先忽略δC与Ploss对系统稳定性的影响。据图4 的系统框图，可以得到：

根据式（9）、式（10），可以将MGP 电压反馈控制进行进一步化简，得到系统的开环增益为：

通过分析系统的开环增益，可以得到系统关于比例系数Kp的闭环根轨迹与极点在虚轴左半平面的运动情况，最终可确定出能使系统稳定的kp的范围。

在能保证系统稳定的Kp范围内，选取使控制系统的阻尼比接近于0.707 的多组Kp参数，作出对应的系统Bode 图与单位阶跃响应曲线，综合考虑相位裕度、幅值裕度、峰值时间与超调量等性能指标，选取控制效果最优的Kp参数，作为最终的参数整定结果。

2.2.3 积分系数Ki的选取

为分析积分系数对系统稳定性的影响，将传递函数转换为以Ki为增益的广义传递函数，由于控制器C的传递函数为式（8），此时控制系统开环传递函数为：

将2.2.2 小节中选取的Kp参数代入式（12）并化简为Ki·GKp=-1 的形式，即可得到关于Ki的等效开环传递函数GKi。系统的广义开环增益如式（13）所示：

根据系统的广义开环增益，可以绘制出控制系统关于Ki的广义根轨迹图。通过观察根轨迹中极点在虚轴左半平面的运动情况，即可确定Ki的合适范围。

在能保证系统稳定的Ki范围内，选取多组Ki参数，作出系统Bode 图与单位阶跃响应曲线，对比控制系统的性能指标，最终选取最优Ki参数。

3 MGP控制参数整定的仿真实验

本节通过在仿真软件PSCAD/EMTDC 中搭建光伏经MGP 并网的仿真模型，对直流电压反馈控制中涉及的控制参数进行整定，并将整定结果应用于同容量的MGP 实验平台，对控制参数的准确性进行验证。

3.1 控制参数整定

在PSCAD/EMTDC 中搭建5 kW 光伏经MGP并网的电磁暂态仿真模型，主电路如图5 所示。仿真所用的实验系统和同步机的参数如表1 所示，控制环节根据图3 进行搭建。

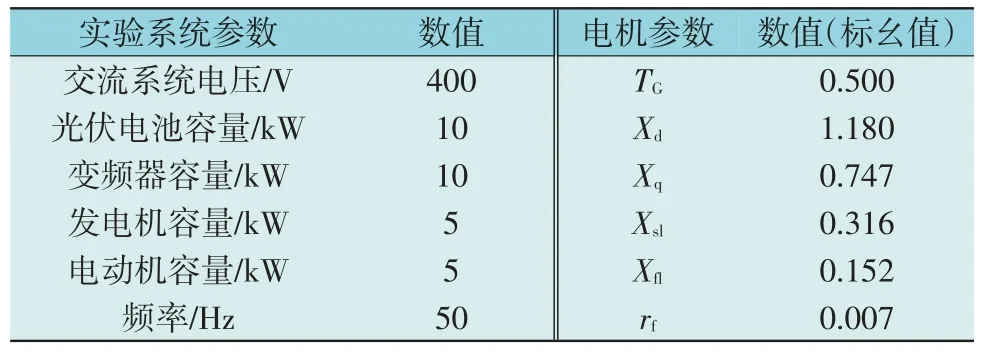
表1 实验系统与5 kW同步电机参数Table 1 Parameters of experimental system and 5 kW synchronous motor

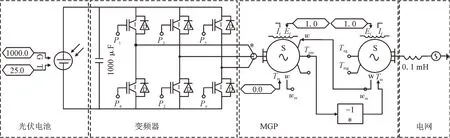
图5 光伏经MGP并网的PSCAD模型主电路Fig.5 Main circuit in electromagnetic transient simulation model of photovoltaic grid connection using MGP in PSCAD

图5 中，G，T 分别为光伏电池元件的光照强度与温度；P1-P6为晶闸管的触发脉冲；Tm，ω为输入同步机的机械转矩与转子转速；ωm为同步机输出的转子转速；Ef为输入同步机的励磁电压，If为同步机输出的励磁电流；Tem为同步电动机输出的电磁转矩；Teg，Tmg为同步发电机输出的电磁转矩与机械转矩。

首先根据发电机的功率-功角曲线，计算出系数kδ-G=kδ-M=0.01，时间常数TG=TM=0.5 s，MGP 系统的比例系数kδ-MGP=0.01，时间常数为TMGP=1。因此传递函数G1～G3可表示为：

本仿真设置的光伏PV 曲线为：端电压为560 V时，光伏输出有功功率为5 kW。故根据2.2.1 所述，MGP 输出有功功率与光伏端电压间的传递函数G4=70。下面整定PI 控制器中的Kp与Ki参数。

3.1.1Kp的参数整定

先令PI 传递函数中Ki=0，将得到的G1～G4代入式（9）与式（10），即可得到控制系统的开环传递函数GKp，如式（16）所示。系统的根轨迹如图6 所示。

图6 控制系统关于kp的闭环根轨迹图Fig.6 Diagram showing closed loop root locus of kp for control system

由图6 可知，不论Kp取何值，特征方程的根都在左半平面，系统都可以稳定运行。当Kp=0.11 时，控制系统的阻尼比接近于0.707。这里取Kp=0.11，0.20，0.30，0.40 作Bode 图，如图7 所示，并研究控制系统的范围阶跃响应，对比不同Kp的值对系统稳定性的影响。

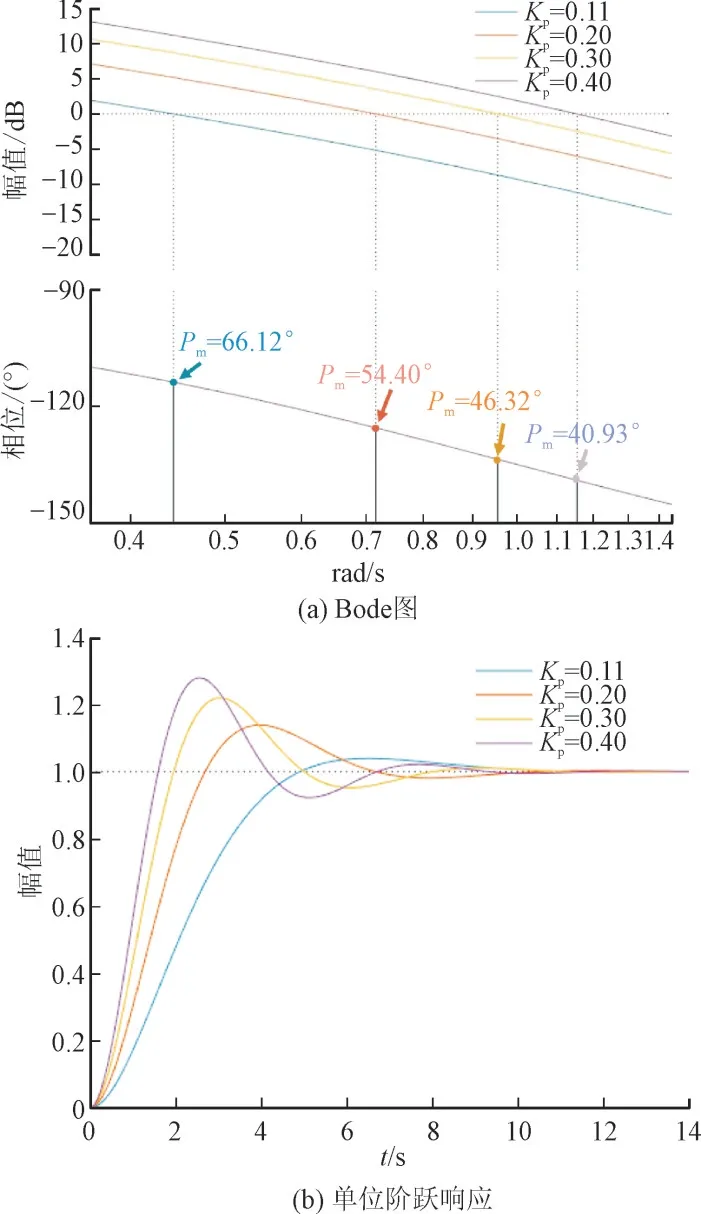
图7 不同Kp取值时控制系统的Bode图与单位阶跃响应Fig.7 Bode diagram and unit step response of control system with different values of Kp

根据图7 可知，当Kp=0.11 时，控制系统的相位裕度最大，超调量最小，阻尼比更加接近于0.707，故选为最终参数。

3.1.2Ki的参数整定

将Kp=0.11 代入式（17）—式（20），可得系统关于Ki的等效开环传递函数Gki，如式（17）所示：

将式（17）代入式（13）所示的系统广义开环增益，可以绘制出控制系统关于Ki的广义根轨迹图，如图8 所示。

图8 控制系统关于Ki的广义根轨迹图Fig.8 Generalized root locus of Ki for control system

根据图8 可知，当Ki=0.107 时，特征方程的极点穿过虚轴，进入非稳定运行区。当Ki=0.01 时，系统的阻尼比接近于0.707。取Ki=0.01，0.02，0.03，0.04，作控制系统的Bode 图与单位阶跃响应曲线，对比不同Ki的值对系统稳定性的影响。

根据图9 可看出，随着Ki的减小，控制系统的相位裕度减小，单位阶跃响应的超调量增大，峰值时间减小。从保证系统稳定性的角度考虑，本文取Bode 图中幅值裕度最大时对应的Ki，即Ki=0.01。

3.2 仿真验证

取Kp=0.11，分别取Ki为0.01，0.02，0.03，0.04，输入至PSCAD 光伏经MGP 并网仿真模型的PI 控制器中，设置光伏端电压参考值为560 V；仿真运行到5 s时，将光伏端电压参考值改变至590 V。光伏端电压波形、MGP 输出有功功率分别如图10（a）和10（b）所示。

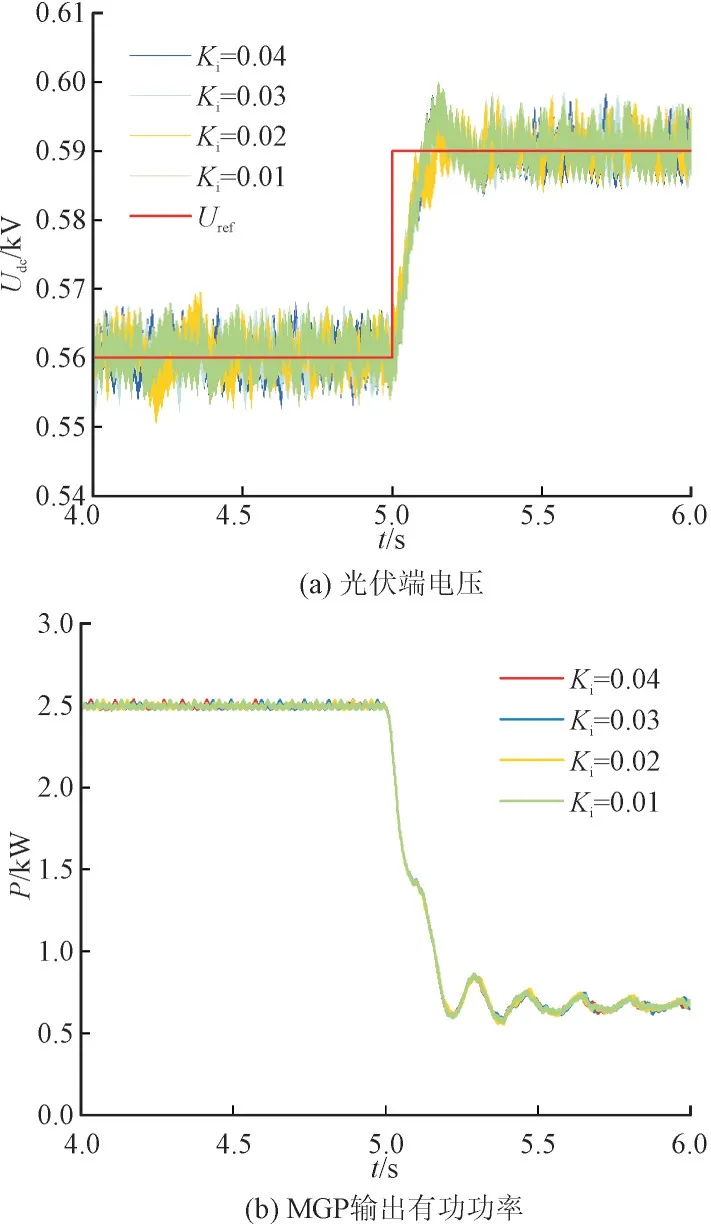
图10 光伏端电压与MGP输出有功功率Fig.10 Photovoltaic terminal voltage and MGP output active power

根据图10 可知，当Ki取值不同时，光伏端电压Udc都能跟随设定值变化，但Ki=0.01 时，Udc的波动最小、进入稳态的时间最短；MGP 输出有功功率略有波动，但基本能维持稳定。仿真结果说明，MGP电压反馈控制的控制参数整定结果准确，整定方法合理，系统可以稳定运行，且具有较高的稳定性。

4 MGP控制参数整定的实验

通过搭建5 kW 光伏经MGP 系统并网实验平台，对第3 章整定的控制参数进行验证。实验平台如图11 所示。

图11 光伏经MGP并网的实验平台Fig.11 Experiment platform of photovoltaic grid connection using MGP

图11 中，PLC 为可编程逻辑控制器，用于输出控制信号。设置光伏模拟器的PV 曲线与PSCAD仿真一致，在PLC 中分别设置两组控制参数：（1）采用工程经验法得到的控制参数，即通过工程运行经验与尝试后得到的能让MGP 稳定运行的控制参数；（2）采用本文所提理论计算法整定出的控制参数，即4.1 节中整定的控制参数Kp与Ki。设置光伏端电压参考值进行如下变化：（1）从560 V 增加至590 V；（2）从580 V 降低至545 V。通过录波仪记录光伏端电压、MGP 输出电压与电流波形，最终得到光伏端电压与MGP 输出有功功率变化波形，如图12 所示。

图12 光伏经MGP并网的实验结果Fig.12 Experimental results of photovoltaic grid connection using MGP

根据图12（a）可知，当光伏端电压参考值改变时，PLC 采用工程经验法与理论计算法得到的控制参数，都能实现光伏端电压对设定值的跟踪，但采用理论计算法对应的端电压波形，稳态时对于端电压参考值的跟踪效果有大幅提升，将稳态时的电压波动从±8 V 降为±1 V，波动减小约87.5%。端电压参考值变化时，理论计算法得到的控制参数下对于端电压的跟踪速度也大幅提升，重新到达稳态的时间从8 s 缩短为2 s，时间缩短约75%。根据图12（b）可知，理论计算法下端电压波形更为稳定，对应MGP输出的有功功率波形也更加稳定，暂态过渡过程更加短暂。

第三章的仿真实验与第四章的实物实验说明，本文提出的MGP 控制参数理论计算方法可以有效提升光伏经MGP 并网系统运行的稳定性，即减小直流侧电压与MGP 输出有功功率的波动，增强直流侧电压对于参考值的跟踪能力。

5 结论

本文通过分析新能源同步机系统的控制特性，研究了光伏经MGP 并网系统控制参数的整定方法，并取得了以下的研究成果和结论：

1）以MGP 的功角特性与功率反馈控制为基础，推导并建立了MGP 系统直流电压反馈控制的频域模型，并通过揭示传递函数中参数对MGP 系统稳定性的影响，制定了用于光伏并网的控制系统参数整定方法。

2）以5 kW 光伏经MGP 并网系统为例，搭建了仿真模型与实验平台，验证了本文提出的控制参数整定方法，相较于传统的工程经验法，可以减小光伏端电压稳态波动约87.5%，减小端电压对参考值的跟踪时间约75%。结果证明本文提出的控制参数整定方法提升了MGP 系统的动态响应性能，为推进MGP 系统的工程应用奠定了基础。