巧用函数的凹凸性，妙解一类曲线切线题

文/深圳市龙岗区龙城高级中学 郭朋贵

近几年高考全国卷中，曲线的切线是高考的高频考点。笔者所在学校的最近一次数学测试中，有如下题目（多选题）：

D.当a=2，b＞0 时，有且只有一条切线

此题如果用常规解法设切线再去求解，无异于做一道解答题，耗时颇多，可不可以小题小做呢？笔者不禁联想到之前研究三次函数切线条数问题，希望从中得到启发.

一、解法探究

关于三次函数的切线条数问题，有如下结论：点P（x0，y0）为三次函数f（x）=ax3+bx2+cx+d（a≠0）所在平面上一点.设函数f（x）的图像在拐点处的切线为l.则有：

如图1，若点P 位于区域I 和区域II 内可作1 条切线；若点P 位于区域III 和区域IV 内可作3 条切线；过拐点N 可作一条切线；若点P 在曲线y=f（x）和切线拐点N 处切线l（点N除外）上，可作2 条切线.此结论省略证明，有兴趣的读者可自行证之.

图1

由可以看出，三次函数图象和其拐点处的切线将平面划分为4 个区域，各区域内的切线条数、曲线和拐点处的切线上切线条数均可以由数形结合直接得出结果. 题目1 会不会也有类似的结果呢？

设过点（a，b）且与曲线y=f（x）相切于点（x0，f（x0））的切线方程为y= f'（x0）（x－x0）+ f（x0），则b =，则过点（a，b）可做切线条数问题等价于函数y=b 与y=g（x）图象交点问题。，且x→－∞，f（x）→+∞;x→+∞，f（x）→0.x 轴为g（x）的渐近线，g（2）=.则有：①a≤0 时，g（x）在（-∞，a），（2，+∞）上单调递减，在（a，2）上调递增＞0.若b＜g（a），0 条切线；若b=g（a）或b＞h（a），1 条切线；若g（a）＜b≤0，2 条切线；若0＜b＜h（a），3 条切线.

②0＜a＜2 时，g（x）在（-∞，a），（2，+∞）上单调递减，在（a，2）上调递增。＞0，g（2）=h（a）=＞0.若b≤0，0 条切线；若0＜b＜g（a）或b＞h（a），1 条切线；若b=g（a）或b=h（a），2 条切线；若g（a）＜b＜h（a），3 条切线.

③a=2 时，g（x）在（-∞，+∞）上单调递减，g（a）=g（2）=h（a）.若b≤0，0 条切线；若b＞0，1 条切线；

④2＜a≤4 时，g（x）在（-∞，2），（a，+∞）上单调递减，在（2，a）上调递增.g＞0，g（2）=h（a）=若b≤0，0 条切线；若0＜b＜h（a）或b＞g（a），1 条切线；若b=g（a）或b=h（a），2 条切线；若h（a）＜b＜g（a），3 条切线.

⑤a＞4 时，g（x）在（-∞，2），（a，+∞）上单调递减，在（2，a）上调递增＜0.若b≤h（a），0 条切线；若b=h（a）或b＞g（a），1 条切线；若h（a）＜b ≤0 或b=g （a），2 条切线；若0＜b＜g（a），3 条切线.

根据以上结论，我们可得出如下结论：

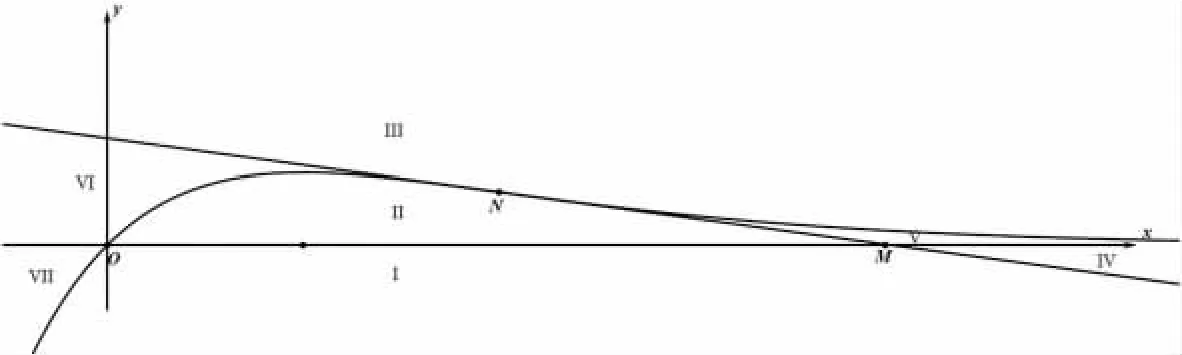
图2

题目1 所得结论与三次函数结论既有相似之处又有不同，三次函数没有渐近线，而题目1 中的函数有一条渐近线，这使得区域划分更加复杂，也为我们数形结合快速解题指明了方向.

二、数形结合图解切线条数问题

例1：已知函数f（x）=x3-3x，a＞0，如果过点A（a，2）可作曲线y=f（x）的三条切线，则a 的取值范围为____.

图解：f'（x）=3x2-3，f''（x）=6x，f（x）有唯一拐点（0，0），在拐点处的切线方程为：y=-3x，且在（-∞，0）为凹函数，（0，+∞）为凸函数.如图3 所示，由图可得答案：a＞2.

图3