浅析长度估测的影响因素——以小学位置估测问题为例

文/北京师范大学南山附属学校 郭国林

测量估计简称估测，是不使用一般的测量工具，以一定的方法推算测量结果的一种心理加工过程。在北师大版数学教材中，位置估测问题通常就是长度估测的问题，往往结合整数的大小比较、生活中的大数、整数的运算、认识方向、行程问题等不同的问题情境，训练学生的长度感知和长度估测能力。从内容安排上看，二年级到六年级都有长度估测的相关内容，是小学阶段重要的数学活动之一。

一、理解能力的影响

小学的数学问题往往是图文并茂的，位置估测的问题也不例外。学生需要认真读题，重视题目中的重要信息，还要重视数形结合。所以阅读理解能力是顺利完成任务的重要前提。

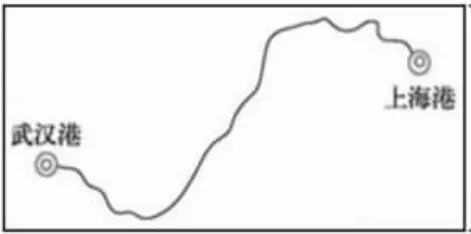
图1

又比如，“春节时张叔叔乘火车从北京途经天津、济南，回青岛老家。 火车平均每小时行驶152 千米，从北京出发，3 小时候大约行驶到什么位置？（如图2）”里程表中3个路程信息不是同一个起点，如果学生没有注重“数形结合”去理解各个数据所对应的起点和终点，就会影响到接下来的长度估测。图3 中，学生把122 和426 进行相加，没有注意到这两个数字相加，部分路程会重复计算，从而误判火车没有驶过济南。

图2

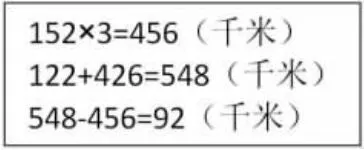
图3

二、长度感知能力的影响

每个人的学习经历、认知发展、社会经验、成长经历是不一样，这会导致个体对长度的感知能力存在差异。学生在估测线段长短时，需要通过自己的观察、分析、比较和判断，建立起一个数值与一段长度之间的联系，数感和长度的感知就显得尤为重要。在图2 中，有的学生计算出火车3 小时行驶了456 千米，从而判断火车驶过了济南30 千米。济南到青岛的这段距离是393 千米，那30 千米应该占这段距离的多少呢？由于学生无法感知“30 千米”和“393 千米”这两个长度，不能很好地进行两者之间的长度比较，导致了长度估测的不精确。

三、估测方法的影响

1.刻画“长度单位”。 长度估测的问题经常会在情境图中出现一个作为参考的测量单位。有的学生没有用笔标出记号，只是通过眼睛观察，在脑海里进行单位长度的分解、叠加；而有的学生会把每一次单位长度的叠加用笔刻画在纸上。由于个体认知的特点，用笔刻画单位长度比在心里叠加长度单位要更加容易，也会让长度的估测更精确一些。

2.寻找分界线索。 这个策略在解答位置估测问题时经常会被用到。有的学生能够很好地进行计算，但是不能有效地在题目信息中找到分界的线索，计算的数据不知道和哪一条线段，哪一个分界点进行比较。如果和不恰当的线段进行对比，往往事倍功半，有时还会出错。

3.利用中心点进行长度估测。 由于人们对“对称”这个感知比较敏感，学生要找到线段的中心点是相对容易的，但是有的学生不会很好地利用这个特殊的位置。

4.恰当使用“化曲为直”的方法。 估测曲线段的长度相对是比较难的，学生潜意识里也会使用化曲为直的策略。

四、估测态度的影响

在心理上，小学生对计算出来的数字会更加地“信服”，而对估算、估测这一类的活动比较随意，这一观点在采访学生时也得到了印证，比如有的学生会说“我感觉大概就是这么长”。尽管直觉、经验也能够帮助学生进行长度估测，但我们在与学生交谈中发现，学生在估测时并未很好地顾及“精确度”，以为估测位置只需“大概”即可，对数据信息与图示长度的关系也没有进行很仔细的对比，答题过于随意，对估测的准确率造成了较大的影响。