宏/细观一体化多尺度数值分析的进展与应用

谭志勇 阎君 宁蕙 吴凡 王淑玉

（1 中国运载火箭技术研究院，北京 100076；2 空间物理重点实验室，北京 100076；3 东南大学机械工程学院，南京 211189）

0 引言

自20 世纪末复合材料热结构在高速飞行器大量应用以来，对复合材料的破坏分析方法得到了广泛重视和快速发展。尽管如此，目前在工程实际中处理热结构强度问题还普遍采用设计-制造-试验同步开展的“积木式”方法，并且留有相当的强度储备。这一方面是由于材料性能的散差，另一方面也表明对于复合材料热结构的力学分析方法还不是十分成熟，并不足以用来支撑工程结构的可靠性评价。这两方面的主要原因都是因为复合材料内部构造的复杂性，由此带来众多交织耦合的非线性破坏形式，传统的宏观唯象强度判据以及基于连续介质理论假设的宏观数值模拟计算方法只能从宏观层面构造材料的本构性能、表征其力学行为。这类方法从Jenkins 在1920 年提出针对各向异性材料的最大应力判据算起[1]，发展至今已有上百年的历史，目前仍有许多难点尚未解决。由于对涉及复合材料性能的内在本质特征、行为控制因素等难点的认识和把控不足，国内外在处理重要的飞行器结构时，仍然十分谨慎甚至很保守地留有相当的强度储备[2]，并常常采用边制造边试验的方法。

在此背景下，采用细观模型模拟材料内部的真实构造、并建立材料细节与宏观结构之间联系的宏细观多尺度建模方法得到迅速发展[3]。经过本世纪20 多年的不断探索、尤其是伴随着计算机硬件能力的快速发展，采用细观力学进行复合材料数值建模和强度分析的方法已获得了长足的进步。尽管它目前还存在着在计算规模和难度大、精度还不太理想、需要的分析参数实际获取困难等不足，但已经取得了公认的成果，成为学术与工程界有希望取得突破的方向。

复合材料热结构力学性能的高精度模拟对多尺度数值分析方法具有迫切的需求，而不同的多尺度数值分析方法具有各自的特点、也有着自身发展面临的问题。本文首先对目前学术界主流的多尺度数值方法进行了分类概述；结合自身的研究探索对宏/细观一体化多尺度方法进行了分析总结、并指出其研究难点和今后的技术发展趋势。随后，以组合连接热结构中最常用的C/SiC 螺栓为对象，给出了采用多尺度宏/细观组合模型的计算结果，结合与试验实测的分析对比，探讨了C/SiC 螺栓的力学特点并提出了相应的优化设计建议。

1 多尺度数值分析策略的特点及分类

以C/SiC 为代表的纤维增强陶瓷基复合材料在尺度上一般按照微观、细观和宏观进行区分，其强度破坏、损伤累积具有明显的结构和尺度依赖性，因此，采用多尺度分析方法将微观-细观-宏观各个尺度的几何特征、应力/应变场状态和损伤信息联系起来是非常必要的。

微观-细观层级的多尺度分析主要是用于构建“纤维尺度”和“单胞尺度”之间的力学性能关系，图1 以C/SiC 材料为例进行了说明[4]。可知这种方法是在材料的碳纤维丝、热解碳界面层等材料尺度考虑问题，主要用于解决材料级的细致模拟，获得某类材料性能参数[5]。由于这类数值模型的单元尺度(µm 量级)与结构产品尺度的巨大差异，使用这种规模尺度的多尺度模型更偏重于分析材料本身的损伤机理、力学行为，从而间接地指导大型热结构的工艺设计。为评价热结构在复杂载荷条件下的强度承载性能、解决热结构的实际应用难点，工程界更多采用了细观-宏观层级的多尺度分析。此处的宏观模型既包括复杂产品(m 量级)、同时还有代表性的典型连接等局部构件(mm 量级)。

图1 连接微观尺度和细观尺度的多尺度方法示意图Fig.1 Sketch of multi-scale numerical method connecting micro-scale and meso-scale objects

多尺度数值分析方法大体可分为几何建模、力学分析模型（应力分析、强度判据以及损伤和性能退化等）、多尺度分析策略3 个不同方面，这里主要对目前国际国内代表性的多尺度分析策略进行探讨：

从分析策略上，多尺度数值分析一般可区分为顺序多尺度方法和并行多尺度方法两大类。其中顺序多尺度方法是最为常用、也是发展最为成熟的方法，它的特点是采用不同尺度模型之间的计算结果传递来建立跨尺度关联。在微观模型中它基于纤维、基体和界面性能参数，计算微观尺度纱线束的力学性能，然后将均匀化后的结果传递给细观模型的代表性体积单元(单胞)；而在细观模型尺度上，则是计算周期性单胞的力学性能，将其作为结构性能参数传递给宏观尺度模型。因此，这种顺序多尺度方法也被认为是基于均匀化方法的多尺度，其基本的技术途径如图2 所示。

图2 顺序多尺度方法的分析策略示意图Fig.2 Schematic diagram of analysis strategy of sequential multi-scale numerical method

从顺序多尺度方法的分析策略可以看出，其特点是操作相对简单、便于实现，比较适用于编织复合材料结构内部细观特征周期性强的情况。因此这种方法在目前的宏/细观数值建模中被普遍采用、发展得相对成熟，并成功解决了许多实际问题[6-9]。一些新的进展包括采用这种多尺度方法建立的三维编织复合材料弹塑性损伤耦合多尺度模型、以及对应构建的三维编织复合材料高温力学行为多尺度分析框架[10]。但是，这种方法存在着较明显的局限性，即它具有代表性体积单元的周期性、对宏/细观尺度的突变和局部缺陷等非周期性特点难以准确描述；同时，强度非线性行为采用参数传递方式的表征较差。

另一种是并行多尺度方法，其特点是针对不同尺度模型同时求解。它形成一种宏/细观不同尺度的统一架构模型，因此也常称为宏/细观一体化多尺度方法。图3 为一个复合材料开孔拉伸的宏/细观一体化多尺度模型[11]。由于它在各个尺度之间是几何、物理强耦合，相邻尺度之间可以互相传递有效参数，有效避免了顺序多尺度方法的不足，适用于材料内部的局部周期性被显著改变的结构，也具有直接应用于热结构产品级的计算优势。这种方法虽然也经过了多年的发展，但目前还存在求解难度大、跨尺度界面上应力集中显著等难点问题。

图3 开孔拉伸多尺度模型的示意图(细观尺度仅显示纤维束单元)Fig.3 Multi-scale model description of tensile specimen with an open-hole (Only fiber-bundle elements are displayed at the meso-scale level)

2 宏/细观一体化多尺度方法的研究进展

2.1 学术界的研究分类与进展情况

较早发展的并行多尺度是基于并行计算策略的有限元方法[12]（FE2method），在该方法中将宏观模型的每一个积分点都分配一个细观单胞模型，宏观模型的计算结果则作为细观单胞的边界条件，再由单胞计算出的力和应力的体积均值作为宏观的力和应力。由于该计算过程需要在两个尺度上分别组装刚度矩阵，因而，这种方法计算量非常巨大。这种思路后续也获得了一些改进，如将其与快速傅里叶变换结合起来，从而避免在细观尺度上复杂的网格划分和刚度矩阵组装，由此提升了计算效率。

Global-Local 是目前并行多尺度的热点方法，具备了宏/细观一体化多尺度的实际物理意义。其基本思想是在全局区域采用网格粗糙的均匀模型，而在局部关键区域采用精细模型，从而实现对结构级产品采用不同尺度的模型直接耦合，将大部分计算成本集中在局部精细结构上。这种方法与全尺寸细观模型和FE2方法相比，计算量无疑将大大减少。然而，由于模型的精细程度不同，不同尺度模型必然存在分界面上的节点不匹配和应力集中的问题，对该问题的解决是宏/细观一体化多尺度计算方法的技术瓶颈和关注焦点。

一些学者[13]采用迭代的方法在两种尺度模型边界上添加位移和应力协调条件，采用映射函数将边界上细观尺度的力和位移与宏观参数联系起来，对其基本分析计算策略可总结如图4 所示。

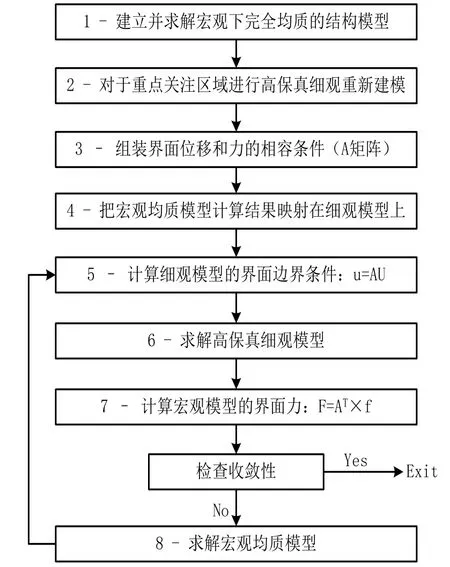
图4 采用Global-Local 宏/细观一体化多尺度方法的迭代分析策略Fig.4 Iterative analysis strategy using Global-Local integrated multi-scale numerical method

从图4 可以看出，这种计算策略具有两个特点：一是虽然建立一个统一的多尺度模型，但宏观尺度区域和细观尺度区域是分别求解的，通过边界条件的不断迭代，来满足计算结果的精度和平滑过渡要求；二是在求解计算时，对于细观模型，迭代的时候是更新界面位移；而对于宏观模型，迭代的时候是更新界面力。

采用力和位移协调条件虽然解决了边界处节点不匹配的问题，但往往并未消除边界处的应力集中。图5 为参考文献[11]对C/SiC 的V 型试验件算例，采用Global-Local 宏/细观一体化多尺度模型的计算结果，看出在宏观模型和细观模型的边界位置仍存在较明显的应力集中。而该应力集中是非真实的，会造成计算结果与真实危险位置、损伤发展趋势不符的情况。而本项目组复验了文献[11]的计算方法，通过使用迭代过程来解决宏/细观不同尺度界面的耦合问题，迭代过程采用位移和力的协调条件来连接不同子域，且通过限制细观尺度上的位移允许解范围来满足宏观尺度在界面处的基函数集合。但得到的结果还劣于图5的算例，这表明当需要考虑复合材料随载荷的非线性特征时，采用这种迭代方法往往达不到理想的效果。

图5 采用Global-Local 直接界面耦合的宏/细观一体化多尺度模型剪切应变计算结果[11]Fig.5 The shear strain results of macro-meso integrated multi-scale model in reference coupled directly with Global-Local interface[11]

与上述方法的思路类似，还有采用Arlequin方法等来进行研究的新文献[14]，在这些方法中，问题域被分解成多个不相连的子域。然后，使用一组Lagrange 乘子重新连接子域，引入这些乘子也是为了加强界面处的兼容性条件。Lagrange 方程和子域有限元问题可以迭代求解，直到子域在Lagrange 力下达到平衡。此外，每个子域可以分别用不同的非共形网格进行网格划分，从而进一步减少运行时间。然而在这些方法中，子域的解耦是基于子域刚度矩阵的分解。因此，这些方法虽然可以处理线性和几何非线性问题，但对于解决复合材料力学非线性问题仍然效果不理想。

其它宏/细观一体化分析方面的研究[15]还有基于扰动理论的渐进展开均匀化方法（asymptotic expansion homogenization），方法的基本思想是将结构位移和应力场按小参数渐近展开，通过摄动方法建立控制方程，从而将细观尺度的材料力学参数表示为宏观尺度全场平均值与局部周期性波动的叠加。虽然渐进展开均匀化方法具有严格的数学理论依据，容易控制求解精度，但是对模拟结构的周期性要求非常严格，因此，多适用于理想周期条件的复合材料性能模拟。

为解决宏/细观一体化多尺度模型的界面应力集中和不连续这一瓶颈难点问题，以北京航空航天大学[16]和本项目组为代表，在总结了上述方法存在不足的前提下，共同研究并提出了一种通过在宏细观模型之间添加过渡区域的多尺度建模方法，建立了由细观区、过渡区和宏观均质区组成的有限元模型，如图6 所示。基本思想是在过渡区域采用均质化宏观单元，两端的尺度大小分别与细观模型和宏观模型平滑衔接，并且调节过渡区域的模型刚度参数与之匹配，由此实现对界面处应力集中的有效缓解。在保证过渡区域的等效刚度连续的前提下，使得纤维和基体的力学性能从细观模型边界到宏观模型边界实现了平滑过渡。

2.2 项目组的宏/细观一体化多尺度建模研究进展

项目组采用2.1 节所述的过渡区域宏/细观一体化多尺度建模方法应用于二维编织C/SiC 开孔板拉伸试件模拟，如图7 所示。过渡区域是起到传递载荷和位移的作用，过渡区域一段材料属性与细观模型相同，将材料性能沿拉伸方向进行过渡，使得另一端材料属性与宏观模型相同，从而缓解界面应力集中和节点位移不连续问题。试件拉伸刚度性能主要取决于沿拉伸方向的弹性模量，其他方向的弹性模量影响较小。因此，主要是保证过渡区域沿拉伸方向的等效刚度与细观模型中单胞在该方向的刚度相等。

图7 C/SiC 开孔拉伸试验件的宏/细观一体化多尺度模型及应力计算结果Fig.7 Macro-meso integrated multi-scale model and stress calculation result of C/SiC tensile specimen example with an open-hole

因此，过渡区的弹性模量可以按照线性插值计算得到

式中，E代表各弹性模量参数，下标int代表过渡区，meso代表细观模型，macro代表宏观模型，x为过渡区单元的坐标，f(x)为与坐标有关的过渡函数。过渡区模型与宏观模型直接进行单元节点的tie 耦合。其中对于细观模型的等效弹性模量Emeso是由碳纤维束和SiC 基体各自模量按照混合率公式计算[17]得到。计算时利用ABAQUS 软件中的UMAT 子程序实现了过渡区域材料属性的线性连续过渡。图7 的计算结果表明，在宏观模型、细观模型与过渡区域界面处的应力集中得到了有效缓解，具有很好的应力连续性。表明了该方法在缓解界面应力集中方面的有效性。

进一步采用这种增加过渡区域的宏/细观一体化建模方法进行了典型连接单元的计算，建立的模型如图8 所示。

图8 对C/SiC典型连接试验件采用过渡区的宏/细观一体化多尺度模型Fig.8 The macro-meso integrated multi-scale model by adding transition regions for typical C/SiC connection specimen

对于搭接板在远离开孔高应力敏感区域采用宏观均质模型；在开孔位置则按照2D 平纹编织C/SiC 材料建立细观模型；而过渡区在与细观模型的界面上两者共节点，在与宏观模型的界面上采用tie 绑定，过渡区域的材料属性按照公式(1)~公式(2)计算、并采用Abaqus 的用户子程序UMAT 进行单元赋值。对于螺栓、螺母紧固件采用宏观均质模型。组装的模型中将螺栓头-搭接板、搭接板-搭接板、螺母-搭接板设置为接触平面，摩擦系数0.15，螺母内表面与螺杆绑定并对螺栓施加轴向100N 预紧力。模型计算在边界条件确定和载荷施加时将下搭接板一端固定、对上搭接板沿板长方向单轴拉伸0.1mm。

获得的应力计算云图如图9 所示，其图9(a)为整体模型的加载方向主应力，图9(b)为仅显示细观模型的纤维束单元。可看出应力计算具有很好的连续性和协调性，在跨界面位置不存在应力集中。图9(a)表明，由于连接单元存在厚度方向的局部弯矩，整体应力集中发生在螺栓头根部以及螺母根部位置；而图9(b)表明，C/SiC 搭接板主要由纤维束承受拉伸载荷、纤维束在开孔周边沿着与加载垂直的截面上也会产生明显的应力集中、且应力集中在厚度方向不均匀。典型连接模型计算结果表现出的这些很好的合理性和规律性，是采用直接界面耦合的多尺度建模、将出现明显应力集中条件下无法实现的。可以认为采用过渡区域的宏/细观一体化多尺度模型获得了满意的结果。

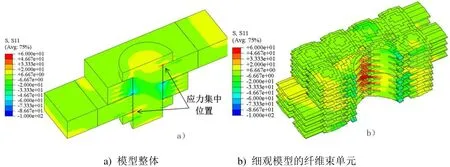
图9 C/SiC 典型连接单元的计算结果Fig.9 Calculation results of typical C/SiC connection specimen

2.3 采用过渡区域宏/细观一体化多尺度建模的强度准则

采用过渡区域的宏/细观一体化多尺度建模目前在强度准则的选用方面仍存在一定的不足。对于参考文献中Global-Local 直接界面耦合的宏/细观一体化多尺度模型，细观尺度模型和宏观尺度模型分别采用了面向均匀化单元、以及纤维束/基体不同组份单元的不同强度准则。这些准则也同样适用于采用过渡区域的宏/细观一体化的宏观模型部分以及细观模型部分。

以图7 算例的宏观区域模型为例，对模型耦合应力状态下的宏观唯象强度准则[18]进行总结。对于轴向受拉σ1＞0 ，σ2=0 的情况，在（1σ ，τ12）坐标平面内采用Tsai-Hill 准则的表达式为

式中，X t是试验件在1 方向的材料宏观拉伸强度，S是剪切强度。但由于该判据没有考虑C/SiC 复合材料拉压强度的不一致，一般情况下与试验值的吻合不好。

若试件存在拉压强度不一致的情况，则一般可选择宏观Hoffman 强度判据，其的相应条件下表达式为

式中，Xc是试验件在1 方向的压缩强度，S是剪切强度。而Tsai-Wu 准则和Hoffman 准则具有相同形式，其效果也相同。

进一步考虑到脆性材料的微裂纹闭合可以使C/SiC 材料的强度和刚度有所增加，则给方程(4)的椭圆包络引入正应力偏移量0σ ，得到修正的Hoffman 准则表示

式中，系数A、B、0σ与试验件在该方向的拉伸、压缩及剪切性能相关，表达式分别为

将式(5)推广到C/SiC 材料的双向复杂平面应力状态，有

上述，式(3)～式(7)的总结说明了对于宏观均质模型采用唯象强度准则是较为完备和成熟的。而对于细观区域模型也可采用应力型或应变型的强度准则[19]。以图8 算例中的细观区域模型为例，若采用应用最广泛的Hashin 准则，它按照纤维拉伸、压缩破坏和基体拉伸、压缩破坏4 种损伤形式，其简化后的三维应力条件下表达形式为纤维拉伸模式（σ11≥0 ）

纤维压缩模式（σ11＜0）

基体拉伸模式（σ22+σ33＞ 0）

基体压缩模式（σ22+σ33＜0）

由式(8)～式(11)看出，对于模拟不同材料组分的细观模型同样可实现完整的强度准则。

对上述强度准则基础上的单元损伤衰减和性能退化方法在本文中不再详细叙述，具体可参阅相关文献[20]。进一步分析这种采用过渡区域的宏/细观一体化多尺度模型，认识到目前存在的技术瓶颈在于：尽管图7 和图8 算例的过渡区域具有满意的应力计算分布，但它是以宏/细观两端各自材料性能为输入、采用拟合过渡的数学算法确定的。因而求得的过渡区域单元的材料性能不具备真实物理含义，也就无法直接采用上述的宏观或细观强度准则。进一步，也难以对过渡区域单元进行以强度判据为基础的损伤衰减分析。这就意味着，对于这种采用过渡区域的宏/细观一体化多尺度建模方法，尽管实现了宏观-细观之间跨尺度的应力计算，但强度分析仍局限于各自的尺度范围内，无疑这是限制其进一步发展提升的难点。

因此，可总结这种采用过渡区域的宏/细观一体化多尺度模型有其适用的场景：即对于需要关注和求解的高应力局部位置采用细观模型、并使得强度分析可包络在此空间内；而对于复杂外形和复杂受力条件的整体部段结构则采用宏观模型。通过宏/细观之间的过渡区域，保证宏/细观模型在整个加载历程的应力传递正确性。在不同的加载步中，宏观模型、细观模型分别按照各自需满足的准则进行强度破坏判别和损伤衰减计算；而过渡区域只承担应力传递功能，不考虑强度破坏和损伤衰减。相应的计算分析流程如图10 所示。

图10 采用过渡区域的宏/细观一体化多尺度模型计算流程Fig.10 Calculation process of macro-meso integrated multi-scale model by adding transition regions

3 对C/SiC 典型元件采用一体化多尺度计算的适用性分析及设计优化

C/SiC 盒型件是采用组装集成设计工艺的大型薄壁加筋热结构的重要基本单元[21]，以此典型元件为例进行了分析。实际的试验件如图11(a)所示，为西北工业大学超高温复合材料实验室采用化学气相沉积（CVI）制备，它采用1K 规格的T300二维正交（0o/90o）平纹碳布叠压成型预制体，最终密度约为1.92g/cm3。对应开展的强度试验评估是对盒型件一端施加拉伸载荷直至破坏，另一端采用挤压夹紧的方式固定，如图11(b)所示。

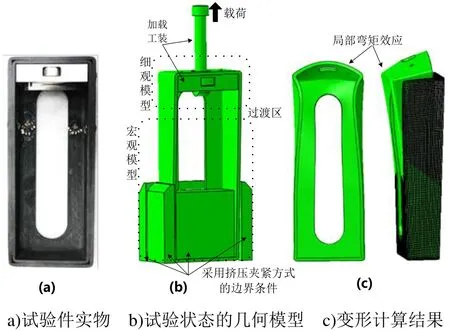
图11 C/SiC 典型盒型件分析Fig.11 Analysis of typical C/SiC box-shaped component

该盒型件有两个重要的结构不连续特征需在体现在数值模型上：一是在细观层面上，盒型件半封闭外形的预制体制备由平面碳布铺成，碳布裁剪使得预制体在四个角边附近具有不连续的情况、在三维高应力情况下将产生耦合复杂的破坏模式；二是在宏观层面上，为协调结构设计厚度与CVI 最佳工艺厚度，盒型件采用了双层嵌套的方式，不连续的双层之间采用SiC 沉积+厚度方向同种材料铆钉加强。

由于均匀化宏观单元难以模拟盒型件的上述复杂特征，在靠近加载点的高应力重点区域适宜采用细观模型进行更详细的模拟；另一方面，盒型件在受载时由于局部弯矩效应使得其变形和应变分布复杂，如图11(c)所示，采用并行多尺度的方法难以按照边界条件信息来准确给出不同尺度模型之间的响应传递。因此，对于该典型单元，最为理想即是采用本文提出的过渡区域连接的宏/细观一体化多尺度建模分析方法。

完成的试验情况如图12 所示，看出盒型件在加载位置附近具有复杂的破坏形貌，结合分析表明不同方向的剪应力组合是强度破坏的主因，且在盒角边附近具有明显的应力集中，双层嵌套间也产生了明显分开。这些同时存在的多种强度破坏模式、涉及不同尺度的非连续性损伤以及不同破坏模式之间的耦合竞争机制，更显现了对结构重点关注区域采用细观方法进行深入描述的必要性。

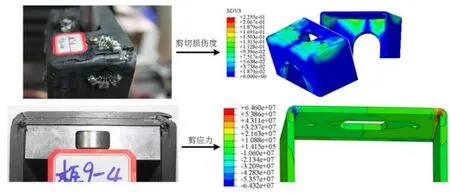
图12 C/SiC 盒型件实际破坏形貌及数值计算对比Fig.12 Actual failure morphology and calculation comparison of C/SiC box-shaped component

试验结果表明，存在多种强度破坏模式一般会导致低应力破坏，而空间结构/载荷的局部弯矩效应是产生复杂应力和多种强度破坏模式的主因。因此对于这种盒型件单元合理的设计优化是改变其受力模式，采用金属辅助垫片使得外载荷跨越通过盒件拐角、再通过盒件侧面板的开孔连接方式产生的钉孔挤压应力尽量与外载荷平衡，保证盒型件主要由各面板承受面内载荷。

4 结论

本文从分析策略角度对复合材料多尺度建模计算方法进行了总结分类。目前的技术现状及实际应用表明：采用顺序多尺度数值分析方法只能在不同尺度模型之间传递等效计算结果，而应力场、应变场以及单元损伤等详细信息还是在各自尺度模型中单独进行分析，难以实现各尺度模型之间所有信息的双向传递，因而宏观结构的应力状态与细观模型的损伤破坏之间的关联性仍不理想。但是由于其具有建模简单方便、计算效率较高的优点，仍是目前多尺度计算的主要方法。

并行多尺度方法通过强耦合着力于解决不同尺度模型之间结果信息的高品质完善传递，目前虽取得了较明显进展但仍存在着技术瓶颈和难点。其中基于并行计算策略的FE2方法计算量过于庞大难以实际应用，渐进展开均匀化方法难以应用于具有非周期特征对象的建模分析。而作为发展热点的Global-Local 宏/细观一体化多尺度方法对于不同尺度模型边界节点不匹配导致的应力集中问题尚未取得满意的计算效果。

本文在分析目前多尺度计算方法特点的基础上，研究提出了一种采用过渡区域的宏/细观一体化多尺度建模方法。分析了这种多尺度建模方法存在的难点是过渡区域内难以给出适用的强度准则判据和损伤衰减计算，并对此提出了合理的应用场景，给出了相应的计算分析流程。

采用这种过渡区域的宏/细观一体化多尺度建模方法进行了C/SiC 开孔拉伸平板和典型连接单元的算例计算，表明不同尺度模型之间应力结果具有很好的连续性和协调性，在有效解决界面应力集中的情况下仍可保持整体模型规模和计算量可控。进一步，以C/SiC 典型盒型件为对象并结合实际试验，通过探讨其力学特点给出了采用这种宏/细观一体化多尺度建模的必要性，并基于已完成的试验和分析结果提出了优化设计建议。

数值模拟是解决复合材料热结构力学性能预测难点、实现其可靠应用和设计优化的必要手段。在后续研究中还需要深入思考如何开发和使用可兼顾模型精度、建模计算效率的数值仿真技术，实现两者的合理平衡，解决现有建模计算方法的局限性并实现满意的工程应用。而以热结构中关键的盒型元件为例说明，采用宏/细观一体化多尺度建模，是在能够建立制备工艺参数、材料细观特征、热结构力学性能三者之间有效关联基础上的有希望途径和分析方法。