基于双树复小波域主成分分析的地震面波压制方法
袁 力
(芜湖职业技术学院 基础部, 安徽 芜湖 241003)
面波是地震信号中一种主要的规则干扰,降低了信噪比,影响信号处理质量.地震记录中的面波一般呈扇形,有能量高、频率低等特点.传统面波压制方法(如F-K滤波[1]、τ-p变换[2]等)主要利用面波与有效信号在频带和视速度方面的不同特征,但压制面波的同时有效信息也会被压制.进一步,根据面波特征在地震记录中估计面波,再在地震记录中减去估计面波,方法有维纳滤波[3]、K-L变换[4]等.2012年Freire等利用奇异值分解(singular value decomposition,SVD)分离地震记录剖面的上行波和下行波[5].
20世纪80年代以来,基于小波变换的面波压制方法不断发展.1996年罗国安等利用面波能量高等特点,在小波域中根据面波的视速度特点作线性时移使面波逐道相干,再作K-L分解估计面波[6].2004年詹毅等将小波包与SVD结合,在小波包处理后联合自动追踪同相轴与SVD进行波场分离[7].2013年Boustani等在曲波域利用自适应SVD压制面波,将曲波域按面波能量比例分为不同区域,不同区域采用不同面波压制方法[8].2020年路鹏飞等将含面波地震信号变换到曲波域,对曲波域系数作傅里叶变换,在此进行面波压制,最后作傅里叶逆变换、曲波逆变换得到压制面波后的地震信号[9].2021年孟娟等利用小波谱能量曲线、经验小波变换等方法压制面波,首先对信号作连续小波变换,根据小波谱得到能量曲线,结合极大值点频率和邻域法确定分割边界,再作经验小波变换得到各固有模态分量,对根据各子频带的频率能量确定的面波模态分量作滤波,从而分离面波和有效波[10].
1998年Kingsbury提出双树复小波变换,增强了传统小波变换,广泛应用于特征提取和数据分析等领域[11].地震信号有多尺度性,有效信号之间有较强相关性,在面波干扰下,反射波能量相对较弱,影响反射波的连续性.双树复小波变换能有效提取和表征地震信号的变化和高维奇异特点.作为常用数据降维方法,主成分分析(principal component analysis,PCA)对协方差阵作特征分解,所得特征向量对应数据的各个主成分,特征值对应数据在各个主成分的权重.PCA变换后各主成分彼此不相关,编号越大的主成分所含信息越少.鉴于此,本文采用二维双树复小波变换与主成分分析进行面波压制.仿真和实际实验处理结果表明本文方法能有效压制面波,保留较多的有效信号信息.
1 双树复小波域主成分分析面波压制方法
1.1 双树复小波变换
可分离小波信号表示其细节特征不好,方向选择少,双树复小波变换(dual-tree complex wavelet transform,DTCWT)解决了此问题.双树复小波具有近似平移不变性,其系数的模有旋转不变性[11].双树复小波分解含两个平行分解树,用两个独立的实小波分别计算实部和虚部系数.实部和虚部滤波器满足希尔伯特变换,实际分解变换中采用双树算法.
图1为一维双树复小波分解变换示意图,其中h0(n)和h1(n),g0(n)和g1(n)分别是树A、树B分解过程的低通和高通滤波器,分别产生低频和高频的实部、虚部小波系数,↓2为下采样.
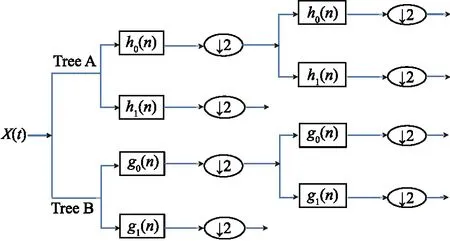
图1 一维双树复小波分解变换示意图
对一维双树复小波作张量积得二维双树复小波变换,即对行和列分别进行一维双树复小波变换.一维双树复小波变换产生2∶1冗余度,而对n维信号,产生2n∶1冗余度.二维双树复小波分解时,各尺度产生2个低频子带和方向分别为±15°、±45°和±75°的6个不同高频子带,均有实部和虚部两部分,对上一尺度的低频子带再进行分解可得多尺度分解,产生不同尺度、不同方向的小波系数[12].对含面波的仿真地震信号作二维双树复小波变换,分解层数为1.分解得到的所有子带系数见图2.
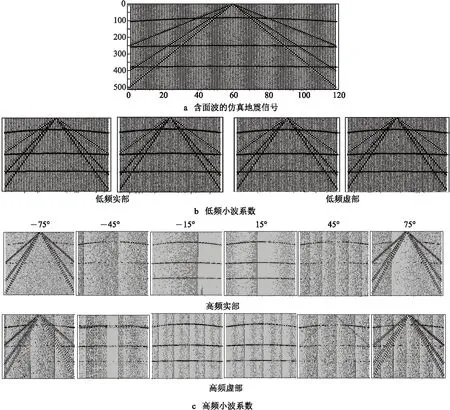
图2 双树复小波变换后仿真信号的各子带系数
图2a为含面波的仿真地震信号,图2b为经双树复小波变换后仿真地震信号的低频子带实、虚部小波系数,图2c为±15°、±45°、±75°各方向高频实、虚部子带小波系数.
图2b显示低频子带中含大量的反射波信息,但同时也含大量的面波信息,因此在该子带应采用合适的方法进行面波压制.在图2c中,±75°实、虚部子带中反射波信息少,而面波成分多,考虑在该子带应用阈值方法压制面波;±45°实、虚部子带中同时含有反射波和面波信息,信息量均较弱,为了更好地压制面波,在该子带考虑进行面波压制;±15°实、虚部子带主要包含反射波信息,面波信息很弱,所以在这一子带考虑保持不变.
1.2 主成分分析(PCA)
主成分分析是一种常用的统计分析方法[13],是对标准化后数据的协方差阵作特征分解,分解后的特征向量即为数据的主成分,各主成分分量之间不相关,特征值越大的主成分所含信息越多,选取特征值较大的几个特征向量,其余元素置零,并取该矩阵的转置作为一个乘法因子,将该乘法因子乘以标准化后数据矩阵就可以得到重构后的新数据.
对地震信号进行双树复小波变换后的小波系数作PCA,由于其中编号大的主成分中含反射波的大部分特征,反射波信息主要包含在前几个主成分分量中,其余主成分主要含噪声信息,利用PCA压制其他信号能量,较好地保留了有效信号信息.
为了说明PCA应用于压制小波系数面波成分的有效性,我们对低频子带系数进行PCA处理,利用PCA处理前、后经双树复小波域变换后合成地震信号的低频子带系数和经双树复小波域变换后反射波的低频子带系数计算信噪比,且选择保留的主成分个数分别为2,6,10,12,16,结果见表1.
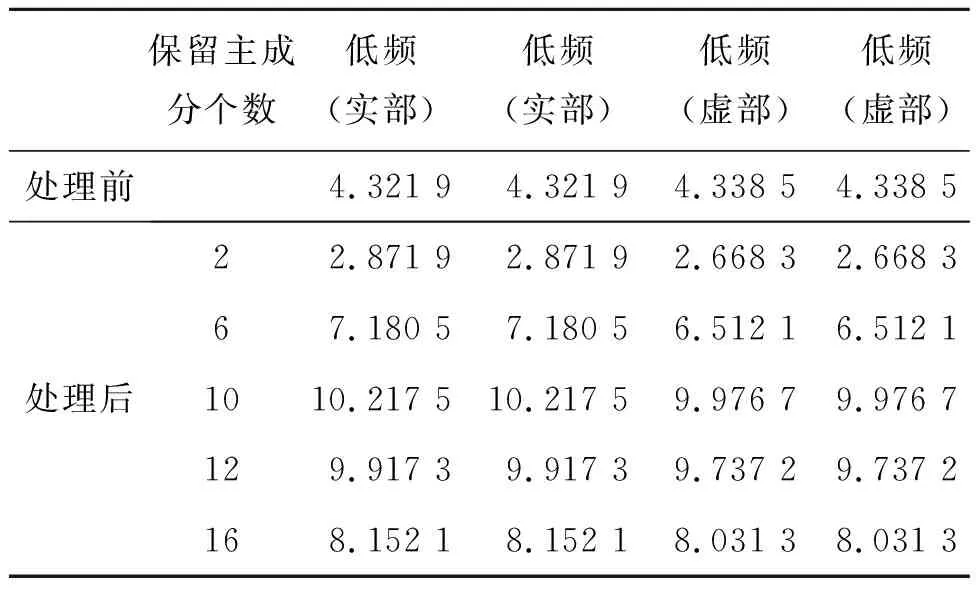
表1 低频子带系数PCA处理前、后的信噪比 dB
观察表1数据可知,经PCA处理后双树复小波域低频子带系数信噪比大多情况下得到大幅提升.PCA处理时,后面的成分仍含有用信息,为了减少重构后的信息损失,选择合适的主成分个数不可忽视.根据实验结果我们发现保留主成分个数为10左右时,信噪比有峰值产生.
为了更直观地显示,我们将图2中低频子带系数和高频±45°实、虚部子带系数进行PCA处理,选择前10个主成分重构,结果见图3.
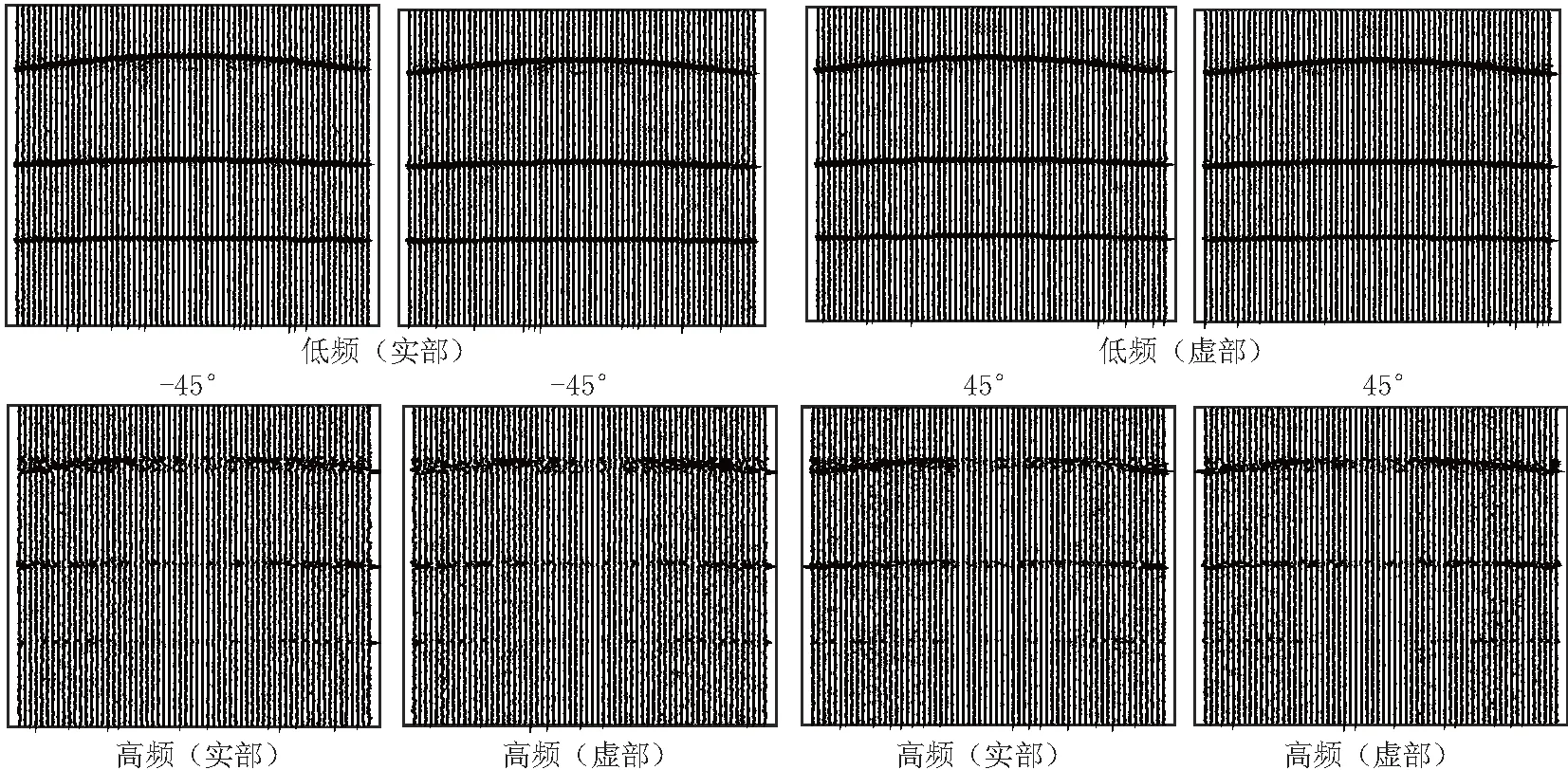
图3 低频和高频±45°实虚部子带系数PCA处理结果图
从图3可以看出,经PCA处理后、小波子带系数中的面波成分得到较好的压制,反射波信息得以保留.本文主要利用PCA变换消除小波系数间的相关性,去除冗余信息,保留有效信息.
1.3 双树复小波域PCA面波压制方法
双树复小波变换具有表示信号高维奇异特征的PCA能力,而PCA是一种较好的特征提取方法,所以本文将两者结合,基于双树复小波,对不同子带区域采用不同方法压制面波.首先对含面波信号作双树复小波变换.由图2知,面波信号主要集中于低频子带和±45°、±75°方向的高频子带中.因此,对低频和±45°高频子带实、虚部系数作PCA处理压制其中的面波成分;对±75°高频子带实、虚部系数作阈值处理;对±15°高频子带实、虚部系数不作处理,旨在压制面波的同时较多地保留有效信号.
阈值方法是经典降噪方法,阈值函数各有优、缺点[14].基于分位数的阈值公式[15]如下:

P(x≤T)=α,
其中:P(·)表示概率,α的取值范围为[0.1,0.3].
基于双树复小波PCA的面波压制方法步骤如下:
步骤1 对含面波的地震信号进行二维双树复小波变换,得到低频和不同尺度方向的高频实、虚部小波系数;
步骤2 对分解得到的低频实、虚部系数均作PCA处理,对各尺度±45°高频实、虚部系数作PCA、±75°高频实、虚部系数作基于分位数的阈值处理,±15°高频实、虚部系数保持不变,得到压制面波后的小波系数;
步骤3 对处理后的小波系数作二维双树复小波逆变换,得到面波压制后的地震信号.
2 实验
2.1 仿真实验
为了测试本文方法的效果,用Ricker子波模拟二维地震信号,在理想地震信号中加入面波信号,得到含面波的合成仿真地震信号.因实际地震信号往往含随机噪声,故仿真实验中的模拟地震信号含面波、反射波和随机噪声.用零均值加性高斯白噪声模拟随机噪声.本文实验均采用MATLAB软件进行编程处理.
为了验证本文方法(DTCWT_PCA_TH)的有效性,将本文方法与PCA、DWT_PCA、DTCWT_SVD_TH、DTCWT_PCA方法进行对比实验:
(ⅰ)将对合成地震信号直接进行主成分分析的面波压制方法记为PCA.
(ⅱ)将对低频和水平方向高频子带作PCA,其余系数不变的普通小波面波压制方法记为DWT_PCA.
(ⅲ)将低频系数均用奇异值分解(SVD),各尺度分解得到的±45°高频实、虚部系数作SVD,±75°高频实、虚部系数作基于分位数的阈值处理,±15°方向的高频实、虚部系数保持不变的面波压制方法记为DTCWT_SVD_TH.
(ⅳ)将低频系数均作PCA,各尺度分解得到的±45°和±75°高频实、虚部系数作PCA,±15°高频实、虚部系数保持不变的面波压制方法记为DTCWT_PCA.
仿真实验中,普通小波基函数为Symlets小波,分解层数为2,双树复小波分解层数为1.利用信噪比(SNR,dB)衡量各面波压制方法的效果,实验结果见图4.

a 压制面波前SNR=-0.801 6 dB

b 压制面波前SNR=0.556 4 dB图4 保留不同成分个数时各方法压制面波后信噪比对比
图4a、图4b分别为加入标准差为15和10的高斯白噪声的各类方法压制面波后的信噪比折线图.横坐标为PCA和SVD重构时保留的主成分个数,纵坐标为信噪比,其中图4a中压制面波前信噪比为-0.801 6 dB,阈值公式中α=0.1.图4b中压制面波前信噪比为0.556 4 dB,阈值公式中α=0.2.由图4可知:
(ⅰ)无阈值的DTCWT_PCA方法和本文方法在两种不同的随机噪声强度下,在一定程度上优于直接对原始数据进行处理的PCA方法和普通小波域PCA方法.
(ⅱ)本文方法和直接对原始数据进行处理的PCA方法其保留主成分个数需取合适大小,实验中保留个数取为[8,12].
(ⅲ)无阈值的DTCWT_PCA方法保留主成分个数过多信噪比反而下降,原因应在于面波压制过少.
(ⅳ)本文方法优于DTCWT_SVD_TH方法,说明双树复小波域的主成分分析阈值方法优于双树复小波域的奇异值分解阈值方法.
地震学里常采用频率波数(FK)方法提取频散曲线,将信号从时间空间域变换到频率波数域,本文采用二维傅里叶变换.再将低频部分移到中心,与频率和波数对应起来,由于离散傅里叶变换谱的对称性,只需取其一半图像,再将负的波数轴取绝对值,得到FK谱.为了更好地显示本文方法的有效性,将PCA、DWT_ PCA、DTCWT_SVD_TH、DTCWT_PCA方法与本文方法压制含面波的合成地震信号的效果进行展示(图5),其中降噪前信噪比为-0.801 6 dB,PCA与SVD重构中保留的主成分均为前10个.
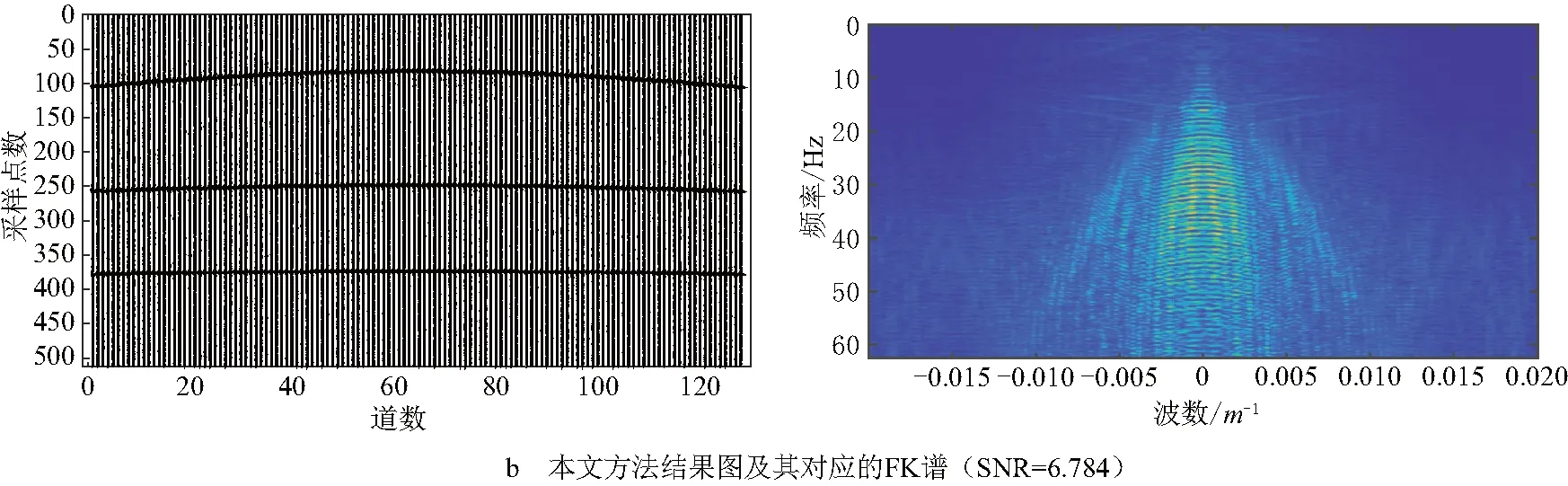


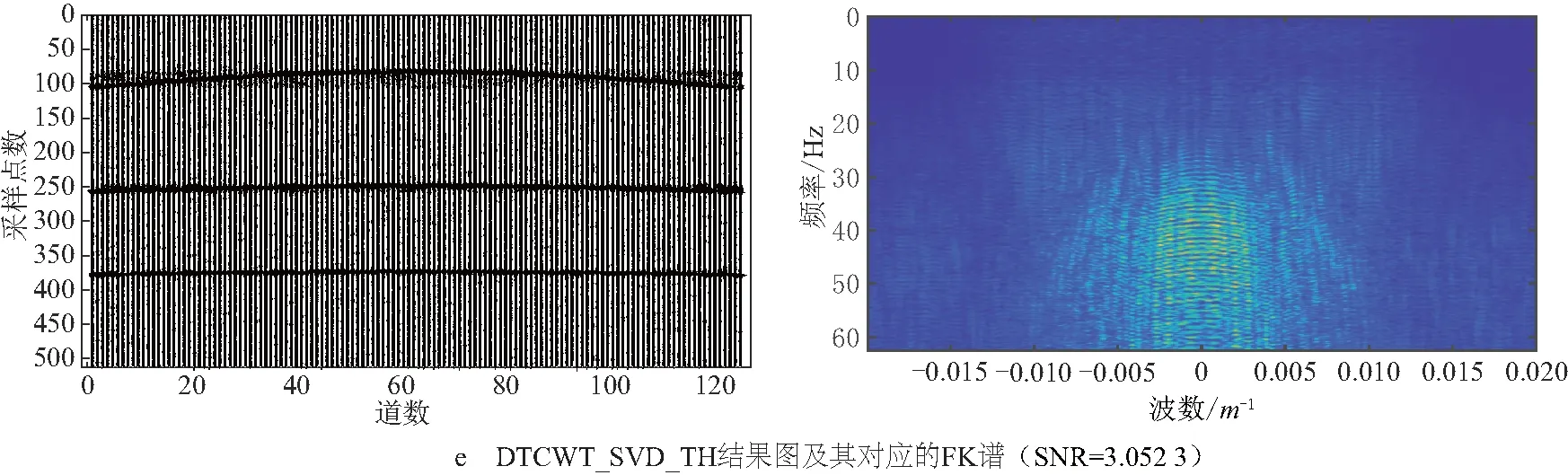

图5 合成地震信号面波压制结果图及对应FK谱图
图5为各方法对合成地震信号的面波压制效果及对应FK谱,其中图5a为含随机噪声的合成地震信号及对应FK谱,图5b为用本文方法压制面波的效果及其对应FK谱图,图5c~图5f分别为用DWT_PCA,DTCWT_PCA,DTCWT_SVD_TH和PCA方法压制面波的效果及其对应FK谱图.从图5c、图5d可以看出DWT_PCA,DTCWT_PCA两种方法的面波压制效果不明显,仍有大量面波信息被保留.从图5e、图5f可以看出DTCWT_SVD_TH,PCA两种方法的面波压制效果明显,但反射波也被压制,有效信号损失过多.从图5b可以看出本文方法较好地压制了面波,且反射波较完整清晰.综合图4、图5,说明本文方法能有效压制面波,保留有效信号的较多能量和特征.
2.2 实际地震信号面波压制实验
在实际地震信号中,面波具有低频率、低视速度、高振幅等特征和频散特性.为了进一步说明本文方法压制面波的性能较好,用DWT_PCA,DTCWT_SVD_TH和本文方法对含面波的实际地震信号压制面波,压制面波后的效果见图6.

图6 实际地震信号面波压制效果图
图6a为原始实际地震信号,图6b为用DWT_PCA方法压制面波的效果,图6c为用DTCWT_SVD_TH方法压制面波的效果,图6d为用本文方法压制面波的效果.图6d信号比图6b、图6c更清晰,面波压制效果更好,说明本文方法面波压制效果较好,大多数面波被滤除,面波压制后有效信号的能量与质量增强,波形变得清晰,该方法在压制面波的同时还去除了较多的随机噪声.
3 结论
双树复小波域的主成分分析方法可以有效压制面波,而阈值方法作为经典降噪方法虽在阈值选取上有其局限性,但本文采用分位数作为阈值选取标准,取得了一定效果.本文在双树复小波域,结合主成分分析方法,基于分位数的阈值降噪方法,有针对性地在不同子带运用两种方法,压制面波信号的同时较好地保留了有效信号.本文还有待改进之处,例如,在双树复小波域可以考虑采用一些更有效的估计有效信号数学模型的方法,如拟合方法等,以期更好地压制面波,恢复有效信号.

