六盘山地区大气加权平均温度本地化模型研究
舒志亮, 桑建人, 刘士军, 林 彤
(1.宁夏气象防灾减灾重点实验室,宁夏 银川 750002; 2.宁夏气象灾害防御技术中心,宁夏 银川 750002;3.成都信息工程大学 电子工程学院,四川 成都 610225; 4.内蒙古乌海市气象局 内蒙古 乌海 016000;5.宁夏人工影响天气中心,宁夏 银川 750002)
六盘山地区位于中国地势第二级阶梯的西部,紧邻第一、二级阶梯的分界线,西南部为四川盆地,东南部为秦岭,处在西风带的中低层和季风区的边缘[1—2],是胡焕庸线经过的地区.六盘山地区属于暖温带森林边界区和半湿润区到半干旱区的过渡带.因青藏高原阻挡而形成的南北气流在此交汇.六盘山地区也是西北内陆地区空中水汽输送的主要通道之一[3—4],在涵养水源、调节气候和保持生态平衡等方面有重要作用.夏季暖湿气流从云贵高原东部两侧沿四川盆地向北行进[5],经常在六盘山地区海拔3 000 m附近形成西南暖湿气流.六盘山是中国为数不多的近南北(与南北方向夹角不足30°)走向的狭长山地,主峰海拔2 942 m,山地东坡陡峭(26°~60°),西坡和缓(20°~35°).六盘山地区的水汽、对流、扩散和催化环境条件得天独厚,是研究空中云水资源开发潜力、实施人工影响天气实验的天然实验室.
根据卫星导航数据在湿空气中传播的延时信息反演大气中的水汽含量(PWV)是计算高精度PWV的方法,于20世纪90年代提出[6].1993年,美国卫星导航系统与地壳形变观测研究大学联合体(UNAVCO)和南加州大学联合进行较大规模的GPS-STORM试验[7],以评估地基GPS 测量PWV的精度.1994年,美国国家海洋和大气管理局(NOAA)与UNAVCO进行GPS-WIS94实验,证明利用GPS可以连续监测大气降水量,其时间分辨率优于1 h,精度达到毫米[8]. 1993年,毛节泰等对地基GPS反演PWV技术进行详细的介绍[9].1997—2017年,陈小雷等在多地开展了卫星导航数据监测、反演PWV实验[10—11],得出影响误差的各种因素以及消除办法,并总结根据卫星导航数据计算整层大气PWV的方法.
根据卫星导航数据计算PWV的原理是卫星发出信号到被地面接收站接收的实际时长.与理论计算的相比,时长有一定的延迟,而造成延迟的介质是大气及其中的水汽.从总的延迟信息中剔除大气延迟信息,得到由大气中的水汽造成的延迟,即大气湿延迟(ZWD).1987年,美国的Askne等推导出电磁信号的湿延迟(ZWD)、水汽含量(PWV)之间转换公式[12]:
PWV=Π×ZWD,
(1)
(1)式中,Π是水汽转化系数,为无量纲系数,计算公式[13]:
(2)
式中:ρw为水汽密度;Rv为水汽气体常数;Mv为水汽分子的摩尔质量;Md为干空气分子的摩尔质量;k1,k2,k′2,k3均为统计或经验常数,分别为77.689,71.295 2,22.974 4 K/hPa,375 463 K2/hPa;Tm为大气加权平均温度(某地大气柱中水汽压权重垂直积分的平均温度[14]).Tm是变量,其他参数均为常数,故无量纲Π与Tm直接相关.
根据卫星导航数据计算某地的PWV,首先根据大气中的水汽压强和温度计算Tm.由于水汽压强和温度的时空差异大,Tm也具有时空差异大的特点.薛琪等基于四川等地的探空站资料[15—16],通过回归分析方法建立本地化加权平均温度模型,并实验证明本地化模型比全球通用的Bevis模型的误差小、精度高.因此提高卫星导航数据反演PWV的精度,要建立本地化的加权平均温度模型.2018年,常倬林等基于卫星导航资料对宁夏云水资源的分布特征进行分析[17],但在反演PWV时使用全球通用的Bevis模型,未建立加权平均温度的本地化模型.有关宁夏通过探空站和微波辐射计资料建立加权平均温度的本地化模型研究较少.笔者基于六盘山地区安装的地基微波辐射计和平凉国家级气象探空站资料,分别建立六盘山地区加权平均温度模型,并对这2个模型进行精度验证.
1 资料与方法
1.1 资料
六盘山地区有微波辐射计1部(隆德)、国家标准气象探空站1个(平凉),两站相距50 km左右.每天08时和20时各观测1次(1 s返回1个数据).根据返回数据的情况,高度变化和分层数不固定.由每次的观测数据形成温湿廓线资料1份,2 a共收集可用资料1 446份.微波辐射计为德国产RPG-HATPRO多通道微波辐射计,每3个月进行1次液氮标定,观测最大高度为10 000 m,固定分93层,1 min返回温湿廓线资料1份,2 a共收集可用资料655 036份(2019-01-01至2020-08-09).为比较基于探空站和微波辐射计资料计算的结果,笔者根据2019-01-01至2020-07-31的观测数据,建立加权平均温度本地化模型,共计645 337个;基于2020-08-01至2020-12-31的9 699个数据对建立的模型进行精度验证.
1.2 Tm的计算方法
Tm的计算方法有5种:(1)常数法.取水汽转化系数Π约为1 /6.5[18],计算得到Tm=269.7 K(有些文献中Tm=281 K[19—20]).该方法计算的Tm精度较低,反演得到的大气中的水汽含量不精确.(2)近似积分法.假设在理想大气中,垂直方向上温度的递减率为常数,且满足大气静力学方程,即根据地面温度、气体常数及重力加速度计算Tm.(3)通过数值预报模式计算Tm.由于数值预报产品的应用不广泛,计算结果存在一定的误差.(4)通过回归分析经验公式计算.根据Bevis等提出的经验公式Tm=70.2+0.72×Ts计算Tm.(5)数值积分法.根据气象探空站或微波辐射计资料得到的气温和相对湿度,再通过数值积分法计算Tm.
基于2019—2020年六盘山地区探空站和微波辐射计资料得到的温度和湿度,利用Goff-Gratch公式((3)式)计算每一高度层的饱和水汽压强[21—23]:
0.786 14.
(3)
式中:ew为饱和水汽压强(hPa);T1为水的三相点温度(273.16 K);T为绝对温度(K);t为摄氏温度(℃).其中,T=273.15+t,t=-49.9~49.9 ℃.
根据ew(hPa)和相对湿度H(%)计算实际水汽压强e(hPa):
e=ew×H.
(4)
然后根据(5)式计算加权平均温度Tm(K):
(5)
由于要沿着整个大气垂直路径,探空站和微波辐射计的高度变化不均匀,(5)式可推导:
(6)
式中:h2,h1分别为两层大气(上层和下层)的高度,因为使用的是两层高度差,这里用海拔高度或者绝对高度,只要全文保持一致即可;ei为两层大气的平均水汽压强(hPa);Ti为两层大气的平均绝对温度(K).
2 加权平均温度本地化模型的建立
根据(6)式分别计算基于微波辐射计和探空资料的Tms,Tmw(图1).由图1可知,根据探空站与微波辐射计资料计算得到的Tms,Tmw变化趋势基本一致,均呈现冬季低、夏季高的特征;受降水影响明显,且在有连续性降水条件下,Tms,Tmw变化剧烈.根据探空站资料计算得到的Tms最大值为291.5 K,最小值为254.7 K,平均值为272.9 K;根据微波辐射计资料计算得到的Tmw最大值为271.5 K,最小值为229.9 K,平均值为249.5 K,二者最大值、最小值和平均值分别相差20,24.8 ,23.4 K.Tms,Tmw是大气柱中水汽压权重垂直积分的平均温度.探空站资料是由探空气球携带探测仪器升空探测得到的,其探测高度约为30 000 m,而微波辐射计的探测高度固定在10 000 m内.对于探测高度在10 000~30 000 m,计算得到的水汽压权重是导致二者差别的最主要原因,这也为根据二者的Tms,Tmw研究高空(万米左右)的水汽变化特征提供了参考.
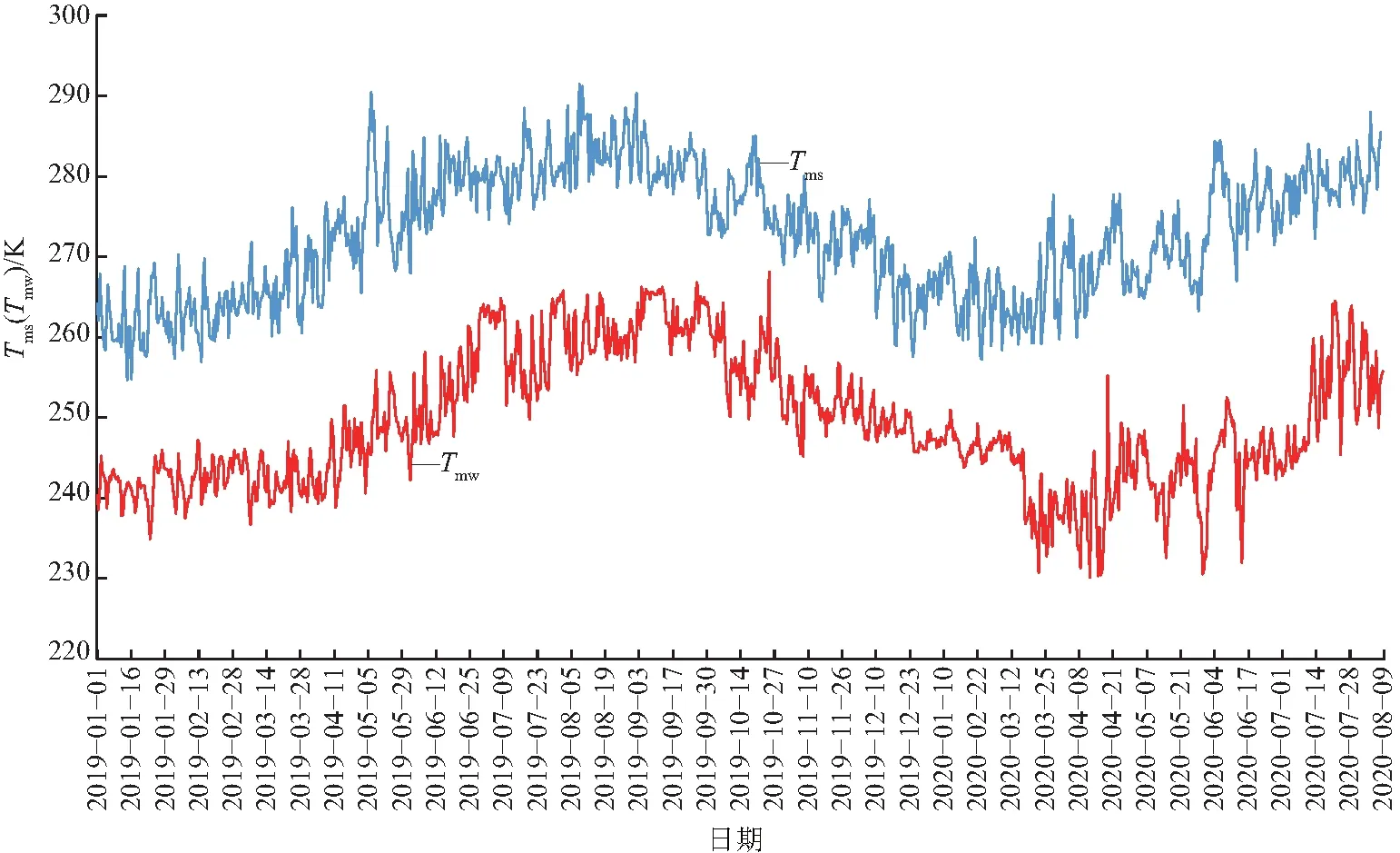
图1 根据微波辐射计(探测高度为10 000 m)和探空站资料(探空高度约为30 000 m)计算得到的Tm
通过最小二乘法,建立加权平均温度Tm和地面温度Ts的模型:
Tms=0.726×Ts+68.545,
(7)
Tmw=0.643×Ts+69.383,
(8)
Tm=0.720×Ts+70.200.
(9)
(7)式为基于探空站资料建立的加权平均温度模型(探空模型);(8)式为基于微波辐射计资料建立的加权平均温度模型(辐射计模型);(9)式为基于Bevis模型建立的全球通用加权平均温度模型(通用模型).
为进一步提高模型的精度,尝试通过最小二乘法,将2019年探空站和微波辐射计资料按月、季、年分别建立加权平均温度模型(表1).由表1可知,基于探空站和微波辐射计资料建立的模型,月、季资料的差异较大,相关性也差,年资料的相关性最好,其次是季,最差的是月.

表1 2019年月、季、年的加权平均温度模型
3 验证模型的精度
根据3个模型计算2020-08-01至2020-12-31的Tm.与根据探空站资料计算得到的Tms(1 d两次,共305个样本)进行对比,与根据微波辐射计资料计算8月1日至10日的Tmw(1 min 1次,共11 371个样本)进行对比,分别验证模型的精度.
3.1 加权平均温度的拟合验证
根据探空站资料计算得到的Tms=250~285 K(图2a),呈散点状分布在探空模型和通用模型的周围.也就是说,基于探空模型和通用模型的计算结果更接近Tms,Tms随着Ts的升高而升高,3个模型的计算结果均呈现该趋势.基于探空模型与通用模型的计算结果几乎重叠,说明两个模型的精度差别较小.而基于辐射计模型的计算结果比其他两个模型的计算结果小22.4 K左右.根据微波辐射计资料计算得到的Tmw=253~268 K(图2b),接近基于辐射计模型得到的计算结果,最大值与最小值之差比根据探空站资料计算得到的差值小得多;Tmw未呈现出随Ts升高而升高的特征,而是呈现片状分布,高值区出现在Ts=285~295 K区域.3个模型的计算结果虽然也呈现出随Ts升高而升高的趋势,但是升高的幅度比图2a小得多.分析其原因,一方面,在根据微波辐射计资料计算Tmw时,除了与10 000~30 000 m的水汽压权重会造成误差有关,还与二者的观测方式、时间、分辨率以及观测期间的天气条件有一定的关系.另一方面,探空模型和通用模型适合模拟探空数据的加权平均温度,辐射计模型适合模拟微波辐射计数据的加权平均温度(10 000 m以下).由于自然界绝大部分的降水是由10 000 m内的水汽转化形成的,辐射计模型更适用于水汽-降水转换效率的研究.
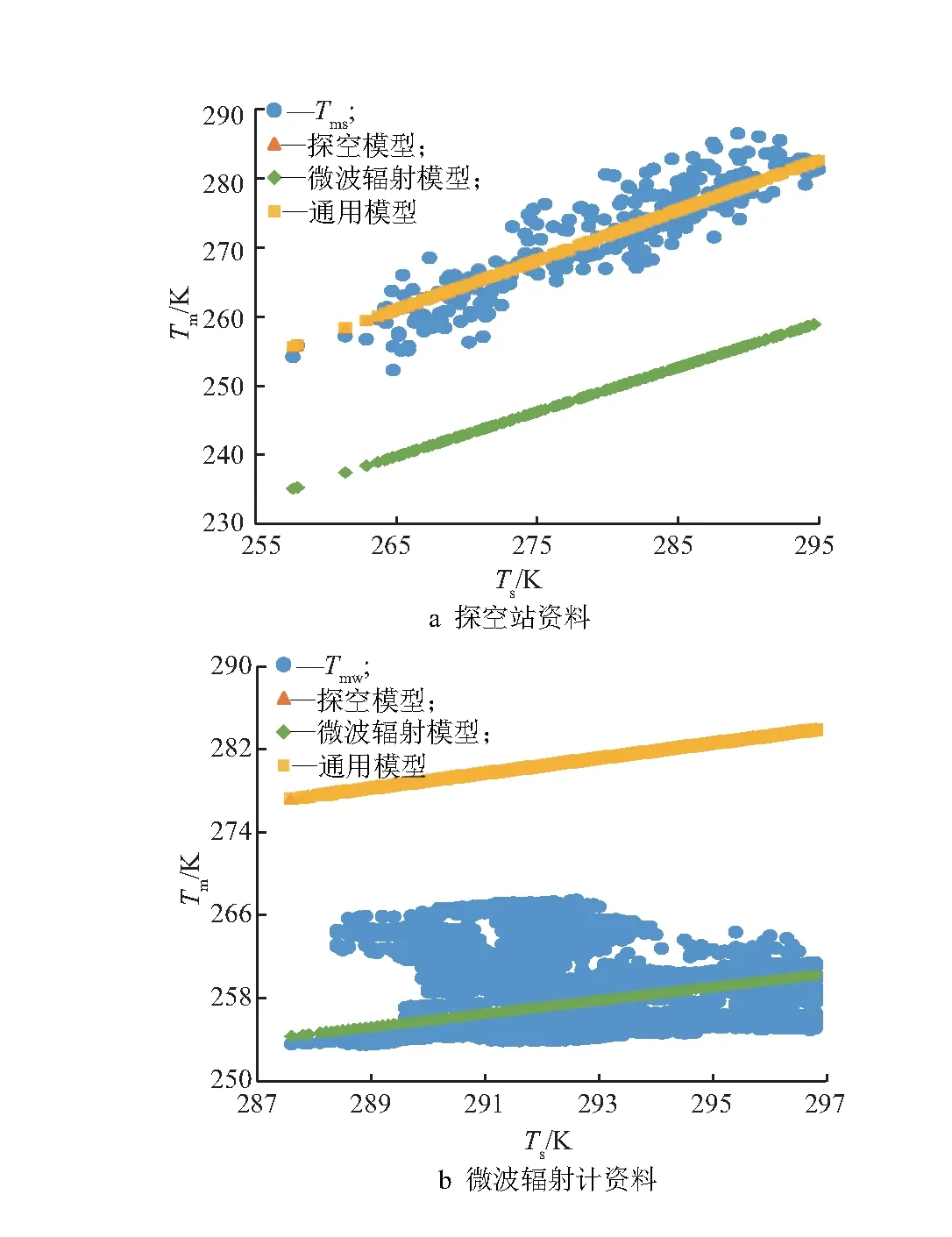
图2 基于不同资料计算加权平均温度的拟合模型
3.2 差值验证
分别对基于3个模型计算得到的结果与基于探空站和微波辐射计资料计算得到的Tms,Tmw,进行差值验证(表2).基于探空模型和通用模型的计算结果总偏差(平均偏差)分别为1.913(0.006),10.36(0.034),表明基于探空模型计算的结果偏差比通用模型的小.基于探空模型和通用模型的计算结果偏离度差别很小,但是基于探空模型的计算结果正负偏离度比通用模型的分别小0.03,0.07.基于辐射计模型计算结果的方差和均方差比探空模型和通用模型的小得多.说明辐射计模型较稳定,但基于探空模型和通用模型的计算结果更接近Tms的方差和均方差(64.48,8.03).对比基于微波辐射计模型计算的结果,探空模型和通用模型的偏差、偏离度、方差以及均方差等均相差不大.但总体上,通用模型要略精确一点,辐射计模型则精确得多,方差和均方差也更接近Tmw(0.55,0.74).因此,在计算整个大气中的水汽含量时,探空模型和通用模型比辐射计模型更精确,而探空模型比通用模型更精确;计算10 000 m内大气水汽含量时,辐射计模型更准确且稳定.

表2 3个模型计算结果的差值
4 结论
1) 根据探空站和微波辐射计资料计算得到的Tms变化趋势基本一致,呈现冬季低、夏季高,受降水影响比较明显的特征.由于探空站气球的探测高度约为30 000 m,而微波辐射计探测高度固定在10 000 m内,受水汽压权重影响,基于二者资料计算得到的加权平均温度的最大值、最小值和平均值分别出现20.0,24.8,23.4 K的差值.
2) 通过最小二乘法,分别建立基于探空站和微波辐射计资料的加权平均温度Tm与地面温度Ts关系的本地化模型:Tms=0.726×Ts+68.545,Tmw=0.643×Ts+69.383. 分析得到的Tm,Ts,发现年资料的相关性最好,其次是季,最差的是月.
3) 精度验证结果显示,基于探空模型与全球通用模型的计算结果差别不大.分析差值,基于探空模型的计算结果的偏差、偏离度、方差以及均方差均比通用模型的精度略高,说明探空模型的实用性较强.
4)在计算整个大气水汽含量时,探空模型更精确;在计算10 000 m内大气水汽含量时,微波辐射计模型更适用.由于自然界绝大部分的降水是由10 000 m内的水汽转化形成,辐射计模型更适用于水汽-降水转换效率的研究.
需要指出的是,该研究只针对六盘山地区1台微波辐射计的资料和平凉站探空资料进行分析,结论是初步的,今后需通过更精确、多源资料进行进一步的分析论证.

