圆柱凸台阵列壁面对液膜强化换热特性影响研究

张皓男，王国峰，赵巧男，徐有宁，张文瀚，郭雨威

（沈阳工程学院a.能源与动力学院；b.工程技术研究院，辽宁 沈阳 110136）

随着工业和农业的迅速发展，能源短缺问题愈发凸显，关于能源高效利用和强化换热的研究得到了多方重视［1］。液膜换热作为一种高效的强化换热方式，不仅可以强化流体的换热效果，还因流量小、热流密度高、传热介质方便易得等优势受到广泛关注［2-5］。当液体在固体壁面上缓慢流动时，液体因受到液滴流动、相间表面张力及壁面粘滞力作用产生厚度量级为100 μm 的液体薄膜（thin film）［5-6］，液膜中液滴出现粘着、反弹、扩散、溅射等不同运动趋势，进而影响水的强化换热［7-9］。近些年，对液膜强化换热的研究已崭露头角［10-13］：文献［14］以多相流VOF 模型作为研究基础，提出相应的数学理论公式，通过数值模拟的方式对气水两相流模型进行了分析；刘梅等［15-16］发现液膜强化换热与模型基底结构密切相关。本文尝试将圆柱凸台阵列应用于基于液膜作用的液膜强化换热研究中，通过改变基底结构与水流初速度提升水幕单位时间内的换热量，以达到增加总换热量的目的。

1 模型及计算方法

1.1 物理模型

为分析液膜理论对强化换热过程的影响，以温室水幕为研究对象并进行简化。假设水幕由两层玻璃板构成，上层玻璃板为平整玻璃板，下层玻璃板上有圆柱凸台阵列，水流从两层玻璃板的夹层中间流过，阳光直射在模型上层的玻璃板表面，下层玻璃板为温室顶盖，与温室内部环境直接接触。假设太阳辐射均匀，水流温度在垂直于流动方向上分布均匀，选取包含5 列凸台的1 个长为1 000 mm，宽为400 mm 的计算域进行研究，所得水幕模型如图1所示。

图1 基于液膜理论的圆柱凸台阵列水幕的物理模型

将该物理模型沿水流方向分成3 个区域：①圆柱凸台阵列上游区，L1=200 mm；②圆柱凸台阵列区，L2=500 mm；③圆柱凸台阵列下游区，L3=300 mm。模型纵向总厚度δ为10 mm，分为5 mm 空气层δa与5 mm 水层δw，水层又分为3 mm 无阻碍区及位于其下方的2 mm 圆柱绕流区。圆柱底圆圆心横向间距P为80 mm，纵向间距S为100 mm，圆柱底圆直径D分别为30 mm、35 mm、40 mm、45 mm和50 mm。

1.2 计算模型

水流在玻璃板间流动时会发生气液分离现象，本文将这种气液分离的水流换热模型定义为气水域流体换热模型，可利用VOF 体积力模型对其换热特性和流动特性进行求解。求解时，既要分析水层和玻璃层的热传导关系，又要分析空气层、水层与玻璃层的对流作用，以得到该模型在不同边界条件下的温度、热流量等参数。控制方程如下：

式中，ρw为水层密度；αw为混合流体中水的体积分数；∇为表面梯度算子；为水层速度向量为质量源项；wg为从水层向水蒸气层输运的质量gw为从水蒸气层向水层输运的质量；p为水的压力；μ为水的黏度为重力加速度；为所受外力；h0为水的导热系数；T0为初始水温。

当水流的速度很小时，液滴受到自身流动、相间表面张力及壁面粘滞力的共同作用，在固体表面形成液体薄膜（thin film）并出现附着、反弹、溅射等现象，进而强化水流换热作用。为了描述液膜对强化换热的影响，以气水域强化换热模型为基础，定义了一种基于液膜理论的强化换热模型。该模型适用于低流速流体换热，将其运用到气水域强化换热相关研究中，能够增强水幕单位面积的换热能力，进而增大水幕的换热量。在气水域换热模型基础上，增加求解液膜厚度的源项方程，以求解液膜厚度对传热的影响，分析基于液膜作用的气水域出现的换热值变化趋势。液膜厚度源项方程如下：

式中，H为水层的液膜厚度；为水层的速度向量；Ts为水蒸气与水层交界面的温度；Tf为平均液膜温度；T3为玻璃板下表面的温度imp为液滴撞击壁面所引起的源项；CP为定压比热容。

1.3 边界条件和计算方法

为比较基于液膜理论的圆柱凸台阵列壁面与平整壁面水幕模型的换热效果，探究圆柱凸台阵列水幕强化换热作用的大小与水流入口速度及圆柱凸台底圆直径之间的关系。通过分析两个物理模型算例来研究换热的影响因素，共计19 组数据（不同初速度下，基于液膜理论的圆柱凸台阵列水幕模型的换热值的算例7 组；与圆柱凸台阵列水幕模型相对应的平整壁面水幕模型7 组；换热与圆柱凸台底圆直径的关系算例5组）。

边界条件：

1）初始条件：水流上方的空气是静止的，需将VOF 两相流模型的气相和液相流体分别设置为空气和水；

2）气相入口边界条件：压力入口；

3）液相入口边界条件：速度入口；

4）太阳辐射条件：时间为6 月21 日13 时，地理位置为北纬48°、东经123°，天气晴。

对模型进行数值模拟时，计算域内为定常流动且没有网格畸变。因此，压强-速度求解器选择SIMPLE格式。在空间离散化设置中，梯度为Least Squares Cel based，压力差值为PRESTO，体积分数选用Compressive，能量方程和动量方程选择精度较高的二阶迎风格式，其余方程选用一阶迎风格式，亚松弛因子选用默认值即可满足迭代要求。

2 结果分析

2.1 圆柱凸台阵列对换热的影响

图2 为圆柱凸台阵列水幕模型与平整壁面水幕模型的水流初速度和出口水流温度的关系，横坐标表示入口水流初速度，左侧纵坐标表示出口水流温度，右侧纵坐标表示圆柱凸台阵列水幕模型的出口水温与平整壁面水幕模型的出口水温之差。

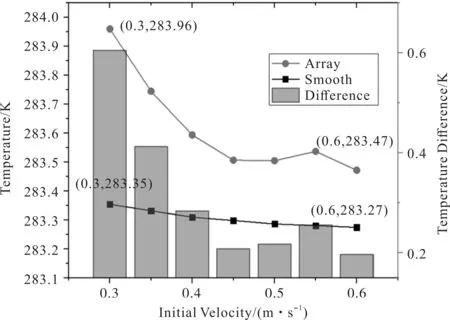
图2 圆柱凸台阵列对出口温度的影响

由图2 可知：水流的出口温度均随入口速度增大而降低，但两种模型受初速度改变的影响程度不同，平整壁面水幕模型的出口温度受初速度增大缓慢减小，圆柱凸台阵列水幕模型的出口温度在低入口初速度范围内（V0<0.45 m/s）受入口初速度增大影响较大，在高入口初速度范围内（V0≥0.45 m/s）受入口初速度增大影响较小。通过比较模型的出口水温的温差发现：圆柱凸台阵列水幕模型出口水流温度要高于平整水幕模型，当V0=0.3 m/s 时，温差最大，为0.605 K；当V0=0.4 m/s 时，温差值降低较多，为0.284 K；当V0≥0.45 m/s时，温差在0.021 K处上下波动。这种现象的出现是由于水流在低流速范围内有较强的液膜作用，水流与水幕内圆柱凸台壁面间由于液膜作用产生粘性剪切力，减小水层向下的速度，而当入口初速度较大时，液膜作用减小，温差趋于平稳。当水流初速度较小（V0=0.3 m/s）时，在1 m 的计算域内，两者温差为0.605 ℃，温室顶盖长为7～8 m，单次循环水流的温升可达4.235～4.840 ℃，其数值相当可观。

图3为入口速度与底面水的体积分数关系云图。

图3 入口速度与底面水的体积分数关系

由图3 可知：当V0=0.3 m/s 时，圆柱凸台下游受圆柱绕流影响，产生明显的扰动现象，在局部出现水流不能完全覆盖玻璃表面的情况；当V0=0.45 m/s 时，圆柱凸台下游受圆柱绕流影响明显减少，扰动现象明显减弱，水流完全覆盖玻璃表面；当V0=0.6 m/s 时，圆柱凸台下游流动较为均匀，几乎不受圆柱绕流影响，扰动现象几乎消失。

图4为入口速度与底面温度关系示意图。

图4 入口速度与底面温度关系

由图4 可知：温度在圆柱凸台阵列上游区的大多数位置保持一致，提升不明显；当水流进入圆柱阵列区后，各初速度下的温度开始不同；V0=0.3 m/s组的算例由于水的流动速度小，水流受到的阳光辐射作用时间较长，液膜作用导致的强化换热影响较大，温升较其余两组大；V0=0.6 m/s 组的算例由于水的流动速度大，液膜作用弱，受到的辐射作用时间短，温升较其余两组小。

2.2 圆柱凸台底圆直径D对换热的影响

图5 为圆柱凸台底圆直径D对模型换热的影响，实线表示圆柱凸台阵列底圆直径D与出口温度的关系，虚线表示圆柱凸台阵列底圆直径D与通过计算域的热流量的关系。

图5 圆柱凸台底圆直径D对换热的影响

由图5 可知：出口温度在总体趋势上随圆柱凸台底圆直径D的增大而增大；当圆柱底圆直径D=30 mm 时，出口温度值最小，为283.484 K；当D=50 mm 时，出口水温最大；除去D=30 mm 和D=50 mm两组数据，其余各组的出口温度随圆柱底圆直径D的增加而缓慢增加。热流量也随圆柱底圆直径D的增大而增大，当D=30 mm 时，通过模型的热流量最小，为1 721.397 W；当D=50 mm 时，热流量最大，为2 273.81 W；除去D=35 mm 和D=40 mm 两组数据，其余各组的热流量随圆柱底圆直径D的增加而缓慢增加。两条曲线的大体趋势是一致的，出口温度和热流量均随圆柱凸台底圆直径D增大而增大，后3 组的热流量和温度数值远远大于前2 组。所以，在此边界条件下，应选直径D>40 mm的圆柱凸台阵列底圆。

图6 为圆柱凸台底圆直径D分别为30 mm、40 mm和50 mm时，模型底面上水的体积分数云图。

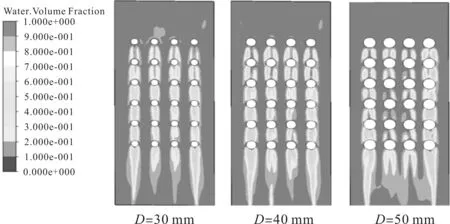
图6 圆柱凸台底圆直径D与水的体积分数的关系

由图6 可知：在圆柱凸台的下游区域，圆柱绕流现象明显，下游出现非对称的气水交替混合区；D越大，圆柱凸台下游受圆柱绕流影响越明显，气水混合区的面积越大；D越小，圆柱凸台下游受圆柱绕流影响越不明显，气水混合区的面积越小。当D分别为30 mm 和40 mm 时，各列凸台下游的气水混合区都是相对独立的；当D为50 mm 时，各列凸台下游的气水混合区连成一片并相互影响。

图7 为圆柱凸台底圆直径D分别为30 mm、40 mm和50 mm时，模型内底面上水的温度云图。

图7 圆柱凸台底圆直径D与底圆温度的关系

由图7 可知：圆柱凸台阵列上游区水层的温度受底圆直径D的变化影响较小，圆柱凸台阵列区和圆柱凸台阵列下游区受底圆直径D的变化影响较大。在下游位置，随着圆柱凸台底圆直径D增大，温度值明显提升；当D=30 mm 时，温度受圆柱绕流影响较小，水层加热较均匀；当D为40 mm 和50 mm 时，温度受圆柱绕流影响较大，水层加热不均匀；当D=50 mm时，温升最大。

3 结论

1）通过对比加入圆柱凸台阵列的水幕模型及平整壁面水幕模型的换热值可知：加入圆柱凸台阵列结构能够显著提升模型的强化换热效果，当入口速度为0.3 m/s 时，仅在1 m 的计算域内，两者单次温差为0.605 ℃。

2）在不同初速度下，基于液膜理论的圆柱凸台阵列水幕模型的入口速度越小，圆柱凸台下游受圆柱绕流影响越明显，液膜作用越强，温升越大；入口速度越大，圆柱凸台下游流动越均匀，受圆柱绕流影响越不明显，液膜作用越小，温升越小。

3）在基于液膜理论的圆柱凸台阵列水幕模型中，圆柱凸台直径越大，受圆柱绕流影响较大，水流加热越不均匀，温升越大；圆柱凸台直径越小，受圆柱绕流影响较小，水流加热越均匀，温升越小。