防烟水幕发生及收缩效应理论与实验

龚红卫,蒋军成,2

(1.南京工业大学 安全科学与工程学院 江苏省城市与工业安全重点实验室,江苏 南京 211800; 2.常州大学 环境与安全工程学院,江苏 常州 213164)

建筑发生火灾时,大量有毒有害烟气在湍流的作用下填满整个疏散空间,降低了能见度[1]并使逃生人员吸入过量颗粒和有毒有害气体甚至导致人员死亡[2-3]。烟气扩散过程中火头温度主要由烟气产生量决定[4]。高层建筑火灾烟气的温度、速度与浓度在横向疏散通道内的变化与建筑楼层有关,发生火灾的楼层离中性层越远,变化越大越快[5-6]。

为了阻挡烟气扩散,常用挡烟垂壁、机械排烟系统、加压送风系统和空气幕等方式来实现[7],火灾初期时挡烟垂壁对延缓烟气扩散有明显效果,随着时间延长,需要采用正压送风等防排烟方式来阻断烟气[8]。正压送风抑制了烟气扩散,但是大量空气进入了火场,降低了排烟效率,而机械排烟量依赖于排烟口的数量[9]。空气幕可以有效地阻止烟气,但烟气控制时间相对较短[10],现有的喷雾式消防水幕主要用于防火与阻隔热辐射[11-13],虽然能在一定程度上减缓烟气的扩散[14-16],但喷射的喷雾颗粒间的孔隙会使部分烟气通过并可能加速烟气的扩散[16-18]。本课题组提出了一种新型溢流水幕[19-20],即以水为介质的连续封闭液膜来控制烟气扩散的水幕防烟系统,该水幕防烟系统是新型的防排烟系统[21],应用于建筑防排烟中可有效地实现对烟气扩散的控制[22]。水幕是由发生装置产生的,水幕发生过程受到水气表面张力、重力和空气阻力等诸多因素的影响,探索防烟水幕水流体流动规律和流动特性具有重要意义。

笔者将通过理论推导和实验分析对防烟水幕发生机制和收缩效应展开研究。在XOZ坐标系下通过对防烟水幕水流体进行受力分析,建立水幕水流体横向运动微分方程,推导水幕水流体横向轨迹方程。分析水幕水流体的横向运动规律,探讨水幕横向运动的收缩效应,并对防烟水幕发生与收缩效应进行实验验证。

1 防烟水幕发生机制

1.1 模型建立

沿水幕边界建立正交曲线坐标系l-s,l为沿水流曲线方向,s为曲线垂直的方向。在沿流线l方向任取一水幕边界微元体,其长度为dl,运动速度为u,初始运动速度为u0,初始水幕水流体取单位宽度,单位宽度流量为qδ。同时，建立沿水平和竖直方向的XOZ坐标系。

X轴正方向为水幕的宽度(横向)向右方向,Z轴正方向为水幕生成垂直或水幕长度(高度)向下方向。θ为水幕水流体横向侧边收缩角(沿水流曲线切线方向与X轴正方向夹角)，水幕边界微元体的XOZ坐标系(x和z为水幕边界微元体在X和Z轴上的取值)如图1所示。

图1 XOZ坐标系Fig.1 XOZ coordinate system

1.2 水幕边界微元体受力分析

水幕边界微元体受力分析见图2。

1)水幕水流体的重力(G)见式(1)。

G=ρgδxdl

(1)

式中:δx为x处水幕边界处厚度,m;ρ为水流密度,kg/m3;g为重力加速度,m/s2。

2)水幕水流体表面张力(Fσ)与表面张力系数成正比,见式(2)。

(2)

图2 水幕边界微元体受力分析Fig.2 Force analysis of micro-cell at the boundary of water curtain

式中:σ为表面张力系数,N/m;R为水幕水流体的曲率半径,通过实验可得边界曲线近似为直线,因此,取R≈1.0。

3)空气阻力(Fτa)与水幕水流体运动速度的平方成正比,见式(3)。

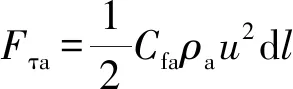
(3)

式中:Cfa为空气阻力系数;ρa为空气的密度,kg/m3。

4)空气对水幕水流体的浮力(Fa)见式(4)。

Fa=ρagδxdl

(4)

5)边界微元体左右两侧面的压力差(Fp)见式(5)。

Fp=ρgξxdb

(5)

式中:ξx为水幕水流体曲率对压力的影响系数;db为水流体宽度在dl中的变化量。

6)剪切力(Fτ)见式(6)。

Fτ=τdl

(6)

式中τ为单位面积剪切力,N/m2。

7)水幕边界微元体X和Z方向的受力分量见表1。

表1 受力分量分析

由表1计算沿X和Z方向的合力Fx和Fz,分别为式(7)和(8)。

(7)

τdlsinθ

(8)

水幕水流体运动时,空气阻力、剪切力、压力差和浮力影响忽略不计,因而式(7)和(8)简化为式(9)和(10)。

Fx≈2σdlsinθ

(9)

Fz≈ρgδxdl-2σdlcosθ

(10)

1.3 水幕运动微分方程和轨迹方程

根据牛顿定律,结合式(9)和(10),运动微分方程见式(11)。

(11)

整理后得式(12)。

(12)

计算水幕边界微元体运动距离,见式(13)。

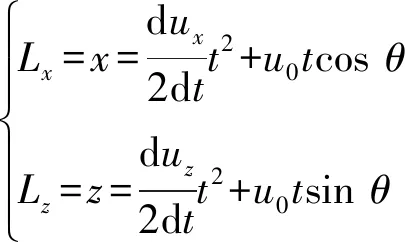
(13)

式中:Lx为水平运动距离,m;Lz为垂直运动距离,m;t为水流体自出射后的运动时间。

为了简化计算,仅在距离推算时,忽略初始运动速度,得式(14)。

(14)

结合式(12)整理得式(15)。

(15)

根据流量(Q)的计算式(16)得式(17)。

Q=ρgδxu=ρgδ0u0x

(16)

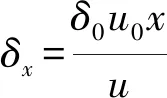
(17)

式中:δ0为水幕初始厚度,m。水幕边界微元体运动速度可以表达为式(18)。

(18)

式中a为加速度,m/s2，计算式见式(19)。

(19)

求解得式(20)和(21)。

(20)

(21)

以上计算过程较为复杂,为了简化计算过程,对水幕边界微元体运动速度进行简化,假定

(22)

将式(22)代入式(21)得式(23)。

(23)

因此，式(15)可以表达为式(24)。

(24)

(25)

z3+x2z=N2x4

(26)

求解整理后,得到水幕运动轨迹方程为式(27)。

(27)

2 水幕收缩效应

2.1 横向收缩系数

为了得到水幕长度方向上宽度的收缩变化,设定X方向水幕初始宽度为b0,z处的水幕宽度为b,其比值为收缩系数α,因此,收缩系数表达式见式(28)。

(28)

由于b=b0-2x,根据式(25)求解得到横向收缩系数表达式,见式(29)。

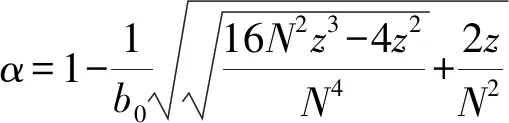
(29)

2.2 横向收缩效应

水幕水流运动随流量的变化有不同形式,当流量较小时,水幕水流的厚度很薄,水流体向下流动时有明显的横向(水平方向)收缩现象,见图3。理论推倒的结果显示水幕运动状态主要取决于表面张力和重力等因素。水幕水流厚度较薄,表面张力的作用显著,水幕横向收缩速度快,水幕断面卷曲变形,并在一定距离处收缩为一点。水幕水流厚度较大,重力作用加速了水幕向下流动的速度,使得表面张力的作用表现相对变小,水幕横向收缩速度相对慢些,但横向收缩不变,水幕断面卷曲变形看上去得到延缓,水幕向下流动到某处收缩为一点。

图3 水幕轮廓形状Fig.3 Outline shape of water curtain

图4(a)为宽度较小的水幕轮廓,水幕水流体出现收缩现象,较快收缩为一点,水流聚在一起后分散下流。图4(b)为宽度增大了的水幕轮廓,水幕水流体依然出现收缩现象,较慢收缩为一点,此时的交点为纵向最远点。图4(c)为宽度较大的水幕轮廓,水幕水流体依然出现收缩现象,但收缩程度较小,在横向保持一定宽度时,水幕出现了破碎现象。

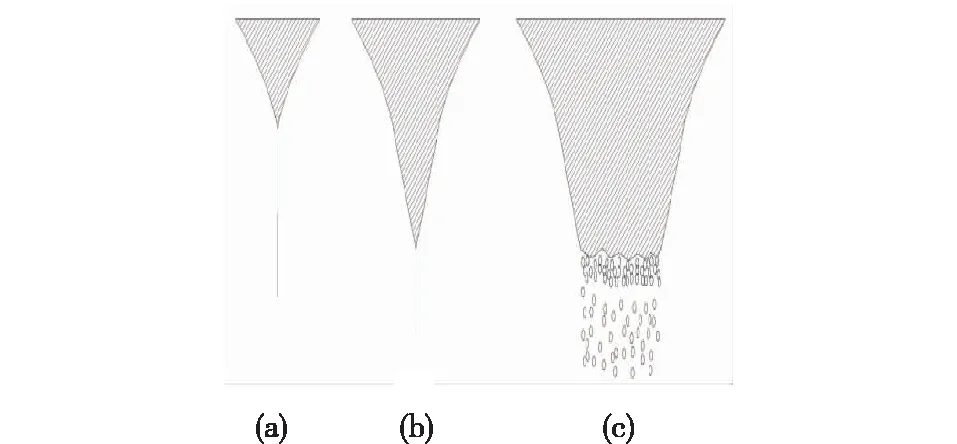
图4 水幕横向运动轨迹Fig.4 Lateral trajectory of water curtain

3 防烟水幕实验

3.1 实验目的

为了验证防烟水幕横向运动理论推导的水幕轨迹方程表达式和收缩系数表达式的合理性以及防烟水幕横向运动时的收缩效应。设置4个工况对不同初始水流厚度的水幕横向运动进行实验。实验所采用的装置为防烟水幕发生实验装置,本实验装置主要包括防烟水幕发生装置(宽480 cm)及测量仪器,利用防烟水幕发生实验装置产生不同初始厚度的连续密闭水幕,在连续水幕形成稳定后,建立XOZ坐标系,测量水幕边界曲线的坐标数据,计算初始厚度及水流量,结果见表2。

表2 各实验工况初始厚度与初始流量

3.2 实验结果与分析

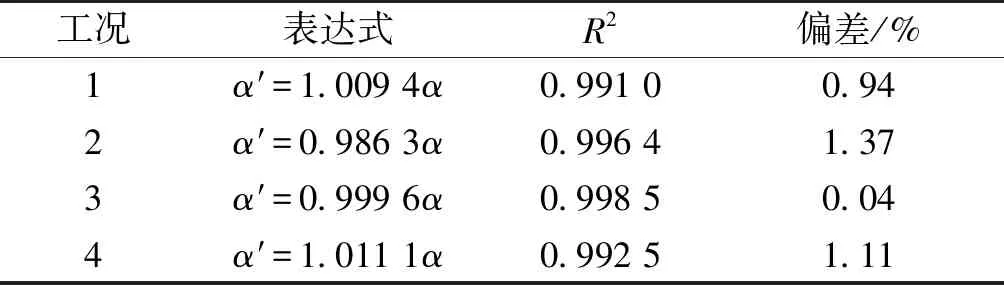
为了记录实验数据,建立XOZ坐标系,间隔取10个测量点对实验结果进行分析。水幕实验图形(图5)皆是沿水幕中心点竖直方向呈对称的图形。初始条件:当x=0、z=0时,水幕长度为0,水幕宽度为480 mm。由于水幕图形的对称性(以x=240 mm的直线为对称轴),当x≤240 mm时,随着x值的增加,水幕长度z值也在增加;240 mm

图5 工况1—4实验图形Fig.5 Experimental graphs of 1-4 working conditions

通过测量图5的实验结果可得:工况1,水幕长度达258.2 mm,水幕底部收缩破碎,然后扩散;工况2,水幕长度达480.8 mm,水幕横向收缩接近一点后水幕底部破碎;工况3,水幕长度达720.4 mm,水幕横向收缩为一点;工况4,水幕长度达922.6 mm,水幕横向收缩为一点。

水幕长度变化以x=150 mm为例进行分析,工况1的水幕长度为177.3 mm,工况2的水幕长度为281.8 mm,比工况1的延长了58.94%;工况3的水幕长度为393.0 mm,比工况2的延长了39.46%；工况4的水幕长度为475.4 mm,比工况3的延长了20.97%。

水幕宽度变化以z=200 mm为例进行分析,工况1的水幕宽度为143.2 mm,相比初始宽度减小了70.17%;工况2的水幕宽度为247.1 mm,比初始宽度减小了48.52%,但比工况1的增加了72.56%。工况3的宽度为306.4 mm,比初始宽度减小了36.17%,但比工况2的增加了24.00%;工况4的宽度为323.2 mm,比初始宽度减小了32.67%,但比工况3的增加了5.48%。

水幕面积变化,工况1—4的水幕面积约为6.53×10-2、10.45×10-2、15.20×10-2和18.82×10-2m2。工况2的水幕面积比工况1的增大约60%,工况3的水幕面积比工况2的增大约45%,工况4的水幕面积比工况3的增大约24%。

分析工况1—4的实验结果,水幕轮廓边界线为两条对称曲线组成,沿Z轴方向,起始端曲率比较大,随着水幕长度的增加,曲率逐渐变小;初始水流厚度对边界轨迹曲线会产生影响,初始厚度越大,曲率变化越大;水幕长度随着z值的增加而增加,水幕宽度则变小。

初始水流厚度或流量增加,水幕破碎或收缩为一点的位置在Z轴方向上也增加;初始水流厚度或流量增加,水幕长度增加,宽度增加,水幕面积增加。

初始水流厚度或流量增加,水幕长度增加,工况3的比工况2的增速减缓了25.54%,工况4的比工况3的增速减缓了52.22%。增加的幅度减缓,直到破碎处。

初始水流厚度或流量增加,宽度增加,工况3的比工况2的增速放缓了66.97%,工况4的比工况2的增速放缓了77.05%,增加的幅度减缓,直到破碎处。

初始水流厚度或流量增加,水幕面积增大,水幕面积增加幅度变小。

实验发现水幕横向边界运动出现收缩现象,水流量越小收缩现象越明显。

3.3 实验与理论比对

实验结果与理论推导公式计算结果进行对比，结果见图6。

图6 工况1—4实验与理论对比图形Fig.6 Comparison of experimental and theoretical graphs of 1-4 working conditions

根据图6对各工况各点的水幕长度实验数据与理论计算数据进行相关性分析,以z表示实验数据,z′表示理论计算数据,相关性分析结果见表3。

表3 水幕长度实验与理论结果相关性分析

由图6和表3工况1—4的水幕长度的实验数据与理论计算数据对比可以看出：实验水幕边界轨迹曲线图形与理论水幕边界轨迹曲线图形基本一致,理论计算数据与实验数据的最低偏差为0.39%,最高偏差为4.22%。随着水幕长度的增大,水幕宽度减小。实验数据与理论计算数据整体变化趋势一致。

根据图6,对各工况各点的收缩系数实验数据与理论计算数据进行相关性分析,以α表示实验数据,α′表示理论计算数据,相关性分析结果见表4。

表4 收缩系数实验与理论结果相关性分析

由表4工况1—4收缩系数的实验与理论数据对比可以看出：理论计算数据与实验数据的最低偏差为0.04%,最高偏差为1.37%。

4 结论

1) 通过防烟水幕横向运动过程的受力分析,建立了防烟水幕流动运动微分方程,推导了水幕水流体轨迹方程式,得到了水幕水流体横向运动收缩系数的数学表达式。

2) 分析了水幕横向运动规律,揭示了防烟水幕发生机制,防烟水幕运动为水气两相流在重力、表面张力作用下的俯射运动。

3) 解析水幕横向运动的轨迹,发现了水幕发生过程中的收缩效应,收缩效应主要原因是横向运动时表面张力作用的结果,收缩效应对成型水幕的宽度维持有破坏作用。

4) 防烟水幕实验表明水幕轮廓边界曲线近似一条抛物线,在初始段运动轨迹曲线曲率半径较小,随着水幕长度的增加,曲率半径变大。

5) 初始水流厚度逐渐变小,防烟水幕收缩效应则愈强烈,初始厚度越小,收缩效应越大。

6) 实验与理论计算结果比较可得,水幕边界实验轮廓曲线图形与水幕边界理论轮廓曲线图形一致,理论计算数据与实验数据的最低偏差为0.39%,最高偏差为4.22%。

7) 收缩系数实验与理论的结果比较可得,理论计算数据与实验数据的最低偏差为0.04%,最高偏差为1.37%。