考虑行人避障行为的元胞自动机模型
徐福顺,丁赛喆,侯亚楠,,翟 越,屈 璐,薄 杰
(1.长安大学 地质工程与测绘学院,陕西 西安 710054; 2.中国科学技术大学 火灾科学国家重点实验室,安徽 合肥 230026)
随着城市人口的不断增长,各类封闭式建筑场所内的人员聚集众多,交通设施、人行道、体育馆、办公楼大厅、市场和商场等公共场合无论是正常使用或高峰期,还是在紧急情况(如火灾、地震等)下都有大量的行人往来。但建筑物的平面大小及形状、出口尺寸和安全标识的分布仅仅为了达到标准规范所制定的要求,缺乏整体性与系统性的考虑。因此,由于密集人群的活动而引起的各种事故屡见不鲜,造成人员伤亡、经济损失以及社会影响十分巨大,例如2014年发生的上海外滩踩踏事件,造成36人死亡,49人受伤[1]。
为了探究行人运动的原理,解决室内建筑布局和出口位置布置的合理分配问题,缩短人员疏散时间,减少人员伤亡和财产损失,国内外学者进行了一系列的研究。Helbing等[2-4]建议将行人的运动描述为受社会力的影响,提出了社会力模型。Henderson等[5-6]将气体动力学和流体动力学模型与步行人群的经验数据比较,利用传统的流体力学理论模拟人体运动。宋卫国等[7]在元胞自动机中引入社会力模型中的排斥力和摩擦力,使行人下一步的移动概率受周围行人和障碍物的影响,并且其排斥概率、摩擦概率与人员的移动速度有关。胥旋等[8]在元胞自动机中引入行人的绕行效应,使得在出口堵塞时,行人能够选择周围相同距离的空元胞进行移动,从而选择更为合理的路径。魏成杰[9]根据马尔可夫模型的特点,认为行人下一时刻的速度大小主要根据行人当前状态和状态转移矩阵结合一个截断高斯函数选取,而与上一时刻的状态无关,使得疏散模型既实现了行人与周围环境的信息交互,又能很好地体现移动过程中的随机性。
近年来,贾晓璐[10]发现,若在室内布置空间障碍物,那么行人就会在行走过程中出现躲避障碍物的行为,而在躲避过程中,空间障碍物的前方会存在一个未被行人进入的区域,称之为“避让三角区”,该区域是行人提前避让障碍物所形成的,在行人经过障碍物后,由于其偏向内侧靠拢,因此会形成一个“收束三角区”。
此外,Adrian等[11]认为,即使房间内不存在空间障碍物,在特殊情况下,也有可能会出现“避让三角区”的现象。在行人离开出口积极性(即希望尽快离开出口的强烈程度)不同的情况下,初始人数、出口宽度等一系列因素保持不变,在行人离开房间的积极性较低时,在出口两侧出现了“避让三角区”,这是由于行人将墙壁视为了障碍物,因此会在触碰到墙壁前提前转向;而在较为紧急的情况下,行人则希望尽快离开出口,此时不会出现“避让三角区”。
目前,没有可靠的离散模型能够还原上文所述的有关现象。因此,在文献[11-13]中的经典场域模型基础之上,笔者提出了考虑决策点的改进场域模型,从而实现行人的绕行行为。
1 仿真模型建立
传统的场域模型通过引入静态场和动态场的概念,将社会力模型的理念引用到离散模型中,不仅大大缩短了计算机的仿真时间,同时也能够模拟出与社会力模型相似的行人个体之间的相互作用行为[14]。但是传统的场域模型对于行人整体宏观行为的模拟存在不足,主要存在如下缺点:① 场域模型无法模拟出当行人避让障碍时出现的“避让三角区”以及穿过障碍后形成的“收束三角区”;② 场域模型的静态场规定取元胞到出口的欧式距离进行计算,使得离出口越近的元胞的静态场值越大,这会导致行人可能会近似直线地向前行走,在触碰到障碍物后才会沿着墙壁向出口进行移动,这种现象是不符合实际的;③ 场域模型的更新规则中规定行人在选择下一时刻的位置时,如果行人的Moore领域内的目标点存在障碍物或者行人,则该目标点的转移概率为0。但实际上,若该目标点存在的其他行人在下一时刻离开该位置,那么进行决策的行人是可以选择该点作为下一时刻目标的。
因此,在考虑上述问题的情况下,本文提出了一种改进的场域模型。
1.1 模型环境设置
假设行人流疏散场景为(W+2)×(L+2)(W为宽,L为长)的二维离散网格系统,W×L为行人可以活动的范围,在系统的边界上有一宽度为B的出口[15]。同时,假定疏散场景能见度很高,不存在任何烟雾,无论行人处于系统中的任何一个位置都能够清楚地看到出口且始终朝着出口所在方向行走,不存在后退行为,每个元胞的大小为40 cm×40 cm[16]。
在设置好房间环境后,需要对房间内所有被墙壁和障碍物占据的元胞进行赋值,其步骤如下:
步骤1确定房间出口所在位置,为出口两侧由墙壁占据的元胞赋值。出口两侧第一个被占据的单元格赋值为1,沿出口延伸方向的值逐渐增加。
步骤2由出口侧所在的列(或行)开始,对相邻的列(或行)进行扫描,墙壁单元格(图1中由实线包围的单元格)赋值为1,障碍物单元格(图1中由虚线包围的单元格)首尾两端赋值为1。
步骤3为所有障碍物内部元胞赋值。从障碍物首尾两端开始,越往内部的单元格的值越大。
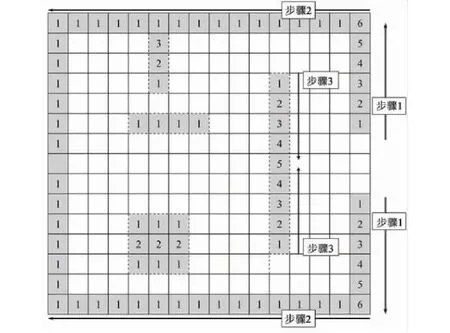
图1 地图扫描赋值流程Fig.1 Map scan assignment process
1.2 决策点运行规则
为了实现行人在障碍物前一段距离提前绕行的行为,现定义决策点的概念。决策点是处在行人正前方一段距离的一个虚拟的点,该段距离规定为dlim,在该点未触碰到障碍物时,行人会朝着出口方向进行直线行走,且决策点会一直和行人保持固定的距离,如图2中的行人从位置1移动到位置2的过程;当决策点触碰到障碍物后,该点就会引导行人提前进行侧向移动,如图2中的行人从位置2移动到位置3的过程,此时行人会选择左侧或右侧进行偏向,决策点与行人距离越近,则行人的转向意愿越强烈,而行人的偏向方向选择取决于决策点左前方和右前方墙壁格点的元胞值,当左侧墙壁元胞值>右侧墙壁元胞值时,行人向右进行偏向行走(图3(a)和3(c)),反之行人向左进行偏向行走。如在图3(a)中,当决策点触碰到障碍物后,读取到左前方的障碍物赋值为4,右前方障碍物赋值为2,那么下一时刻行人将会向右进行偏向行走;而当两侧赋值均相等时,行人则会等概率选择一个方向,例如在图3(b)中,当决策点触碰到障碍物后,读取到左前方的障碍物赋值为2,右前方障碍物赋值也为2,则行人下一时刻选择向左行走和选择向右行走的规划概率比为1∶1。
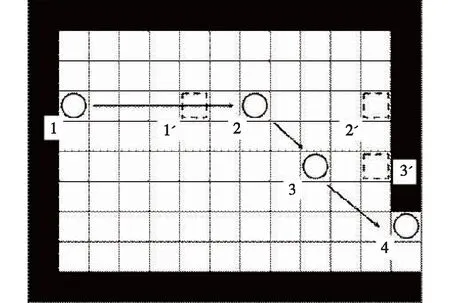
图2 受决策点影响的行人移动轨迹Fig.2 Trajectory of pedestrians affected by decision points
此外,需要注意的是,虽然决策点前方存在墙壁导致行人不能继续前进,但当行人向斜侧移动时,决策点必须紧贴墙壁或障碍物向行人移动方向进行移动,以确保行人与决策点保持在一条直线上(如图2中的位置2′—3′过程)。而当行人成功绕行障碍物时,则决策点和行人之间的距离恢复至临界距离dlim,当行人由位置(i,j)移动到(x,y)时,决策点也会由(iD,jD)移动到(xD,yD)(图3(a))。
1.3 计算公式
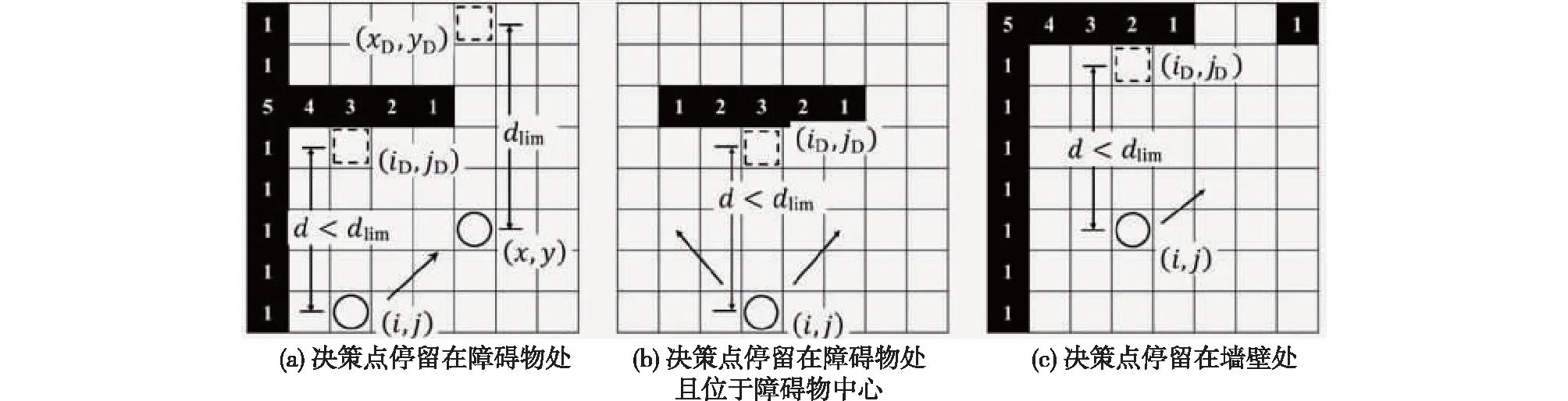
图3 行人在不同位置时决策点的变化情况Fig.3 Changes of decision points of pedestrians in different positions
由经典场域模型可知,行人在每一时刻的位置依据Moore领域的转移概率进行选择,其每个目标格子的转移概率由房间内的静态场和动态场共同决定[17],在本文提出的引入决策点的场域模型下,这一基本规则将发生改变。首先,本文不再考虑为房间整体设置静态场,而是为每个行人设置独立的3×3局部静态场,每个行人之间的静态场值互不影响,其值只由决策点和行人之间的距离来决定;其次,每个行人的3×3局部动态场依然取自房间内的整体动态场值,当有行人移动时,则原位置的动态场值增加,并随时间扩散和衰减。
1.3.1 局部静态场
对于局部静态场来说,其值的计算规律遵循以下两种情况。
① 当d=dlim时,决策点与行人之间无斥力,两者之间始终保持着临界距离,此时行人只向着出口方向直线行走(图4),则在该情况下局部静态场Sij[18]计算式见式(1)。
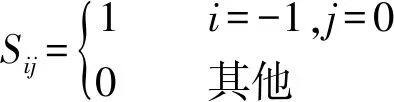
(1)
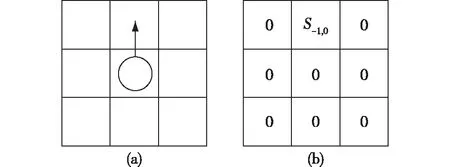
图4 决策点对行人无斥力Fig.4 No repulsion force to pedestrians caused by decision points
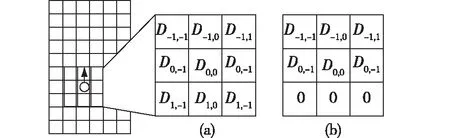
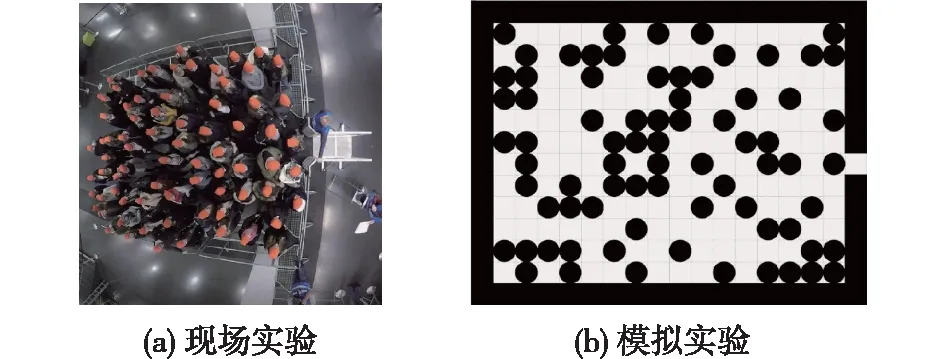
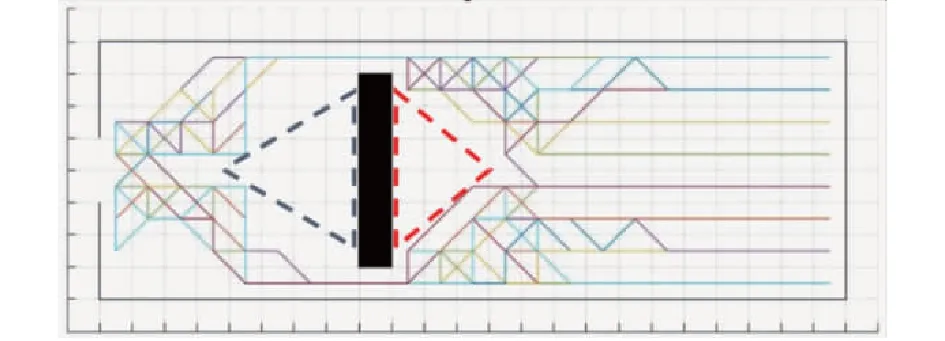
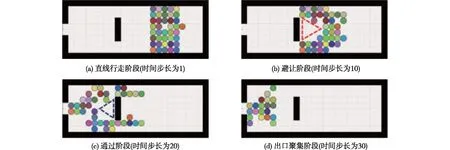
② 当d 图5 决策点对行人产生斥力Fig.5 Repulsive forces to pedestrians caused by decision points (2) (3) (4) 式中:w′Tn用于判断出口位于行人的右侧还是左侧,如果出口位于行人左侧,则行人偏向左侧行走,此时有w′Tn=1;如果出口位于行人右侧,则行人偏向右侧行走,此时有w′Tn=0;Δd为临界距离与行人或决策点实际距离的差值(dlim-d);m为强度系数,用于决定Δd改变对决策点斥力变化的影响,具体表现为对行人移动概率的影响程度;h为距离影响因子,用于决定Δd对γ变化的影响程度;a、β和γ均为偏向系数,分别决定行人偏向正前、左前(或右前)、左(或右)方向元胞的强烈程度,a和β为定值,γ由a、β和Δd共同决定;Ns为局部静态场的归一化因子。 1.3.2 局部动态场 对于局部动态场来说,其值取自以行人在全局动态场中所处位置为中心的3×3矩阵值。而对于动态场来说,其更新规则与传统场域模型保持一致。当处在(i,j)的元胞有行人经过时,则下一步长该元胞的动态场值Dij=Dij+1,其衰减比例系数δ=0.2,扩散比例系数μ=0.1;当某一时刻元胞的动态场值Dij≤0.1,则令Dij=0。 如图6所示,局部动态场值取自以行人在全局动态场中所处位置为中心的3×3矩阵,并且根据前文所进行的假设,为了保证模拟结果符合实际,模型不考虑行人后退行走(后退元胞均为0),因此在该情况下局部动态场值[19]计算式见式(5)。 (5) 式中:(x,y)为矩阵(i,j)在全局动态场中所对应的位置;ND为局部动态场的归一化因子,其计算式见式(6)。 (6) 根据前文所得局部静态场和局部动态场,可以得到行人的3×3移动概率矩阵(Pij)计算式(式(7))。 Pij=N((kDDij)+(kSSij))ξij (7) 式中:kD为动态场敏感度参数;kS为静态场敏感度参数;ξij判断元胞是否被行人占据,有行人取值为0,没有行人取值为1;N为归一化因子,用于确保3×3偏好矩阵的概率之和为1,其计算式见式(8)。 (8) 图6 局部动态场取值过程Fig.6 Taking process of local static field value 考虑绕行行为的决策点场域模型通过计算由局部静态场和局部动态场相互耦合而成的行人Moore领域转移概率矩阵,得到每个行人下一步可能移动的位置,从而实现模拟行人从房间撤离的过程,其具体的求解步骤如下。 步骤1初始化室内环境。给定建筑物的长和宽(W+2)×(L+2)、出口坐标集合、室内空间障碍物集合、行人的数量(n)和编号。 步骤2根据1.1节所述方法遍历整个房间,给所有的墙壁和障碍物赋值。 步骤3.1计算所有行人的决策点位置,通过判断决策点与行人的距离是否小于临界距离,从而利用1.3节中的计算式得到每个行人的局部静态场Sij和局部动态场Dij,代入式(7)得到每个行人的转移概率矩阵Pij。 步骤3.2行人根据转移概率矩阵选择下一时刻希望移动的格点,找到房间内所有存在冲突的行人,比较存在冲突行人的优先度,优先度最高的行人将会在下一步长移动到该格点,而其他行人根据下述情况进行处理:若行人在该步长下为第一次进行选择,则返回至步骤3.1重新进行选择,且未能成功选择的目标元胞概率重置为0,停留在原地的概率增加;若该行人在该步长下为第二次进行选择,则下一步长将停留在原地。 步骤4判断是否有行人到达出口,若有行人到达,则房间内总人数n=n-1。 步骤5判断房间内是否存在行人,若仍有行人停留在房间内,则返回步骤3.1;若所有行人均从房间撤离,则输出模型最终结果。 为验证上述所提出的考虑决策点的改进场域模型的可行性,本节利用Matlab软件构建了与现实环境设置相同的实验场景,观察在此情况下的行人运动以及分布情况是否与真人实验现象相符合。 本节设置了与文献[11]所设置的实验编号030和040相同的疏散场景,为保证环境的一致性,现设置仿真环境如图7所示,环境中房间长为18格(约为7.2 m),宽为14格(约为5.6 m),出口宽度设置为1格(约为0.4 m),室内无任何障碍物。实验开始前在室内随机安置75名行人,当行人移动时即开始计时,所有行人无后退地向出口移动,到达出口后从场景内删除且不再返回。 图7 房间初始设置情况对比Fig.7 Comparison of the initial settings of rooms 分别取行人与决策点临界距离(dlim)为3和7的情况进行仿真模拟,为避免动态场对实验现象的扰动,两次仿真实验均取动态场敏感度参数kD=0.1,静态场敏感度参数ks=0.9。两次仿真实验的模拟结果如图8和9所示。 图8 编号030实验情况下不同时间步长的人员疏散示意图Fig.8 No. 030 evacuation diagram of people with different time steps under experimental conditions 图9 编号040实验情况下不同时间步长的人员疏散示意图Fig.9 No. 040 evacuation diagram of people with different time steps under experimental conditions 通过对比不难发现,在最初始的行人聚集阶段(图8(b)和9(b)),行人从初始位置刚开始移动,故在不同的决策点临界距离设置情况下并无太大变化,但随着时间的进一步推移(图8(c)和9(c)),在dlim=3的情况下,房间内所有未疏散行人聚集在出口附近,形成了一个拱形,即行人自组织行为中最经典的成拱效应,而与之对应的是在dlim=7的情况下,此时房间内人群出现了和前者不同的分布情况,在出口两侧形成了较为明显的“避让三角区”,而由于“避让三角区”的出现,人群呈梯形而非拱形。两种情况下的仿真模拟再现了文献[11]中编号030与040中所出现的两种不同实验现象。 为检验模型的模拟效果,现将模型场景构建在与文献[10]相似的环境中,如图10所示,模型中设置一长25格(相当于10 m)、宽10格(相当于4 m)的走廊,在中央设置一条形障碍物(宽度设置为4格),并设置有无障碍物的走廊作为对比。模拟开始前,在走廊的最右侧会安置5×8=40位行人,模型开始运行后,模拟行人会从最右侧向左侧宽2格的出口进行移动,行人位置每进行一次更新,时间步长就会增加一次,在运动过程中,行人不会越过通道两侧的墙壁,当所有的行人通过最左侧设置的出口后,运行结束。 图10 疏散场景初始化状态Fig.10 Initial state of the evacuation scenario 模型运行后所得到的行人轨迹和行人分布情况如图11所示。由图11行人轨迹图证明,考虑绕行现象的决策点场域模型能够重现人群在室内存在空间障碍物时产生的提前绕行障碍物行为,并且在障碍物前后分别形成了前文所提到的“避让三角区”和“收束三角区”。 图11 行人移动轨迹图Fig.11 Pedestrian movement trajectory map 图12展示的是在不同步长下的人员分布情况。不难发现行人通过障碍物的过程大致可分为4个阶段:① 直线行走阶段。走廊中的行人开始向出口方向进行运动,距离前方的障碍物还有一定距离,此时行人几乎保持直线进行行走,队列较为整齐(图12(a));② 避让阶段。处在该阶段的行人需要避开前方存在的障碍物,因此在该阶段的行人大多聚集在障碍物与走廊形成的瓶颈处,而后方的行人由于提前采取绕行策略,会出现排队等候通过瓶颈的现象,而障碍物前方会形成无人的“避让三角区”(图12(b));③ 通过阶段。通过障碍物后的行人会看到出口所在位置,此时他们会向出口所在位置进行偏向移动,在障碍物后方形成一个向内靠拢的“收束三角区”(图12(c));④ 出口聚集阶段。所有行人通过障碍物后,在出口附近开始聚集,此时人群的整体形状趋向于倒梯形,在该阶段的行人将以稳定的出口通过率离开走廊,直至全部行人离开,运行结束(图12(d))。 图12 不同步长下的人员分布情况Fig.12 Distribution of people under different time stops 基于决策点的改进场域模型通过事先对环境内的墙壁和障碍物赋值,制定决策点与行人的规定临界距离,并利用决策点读取其墙壁或障碍物场域值的方法,实现了行人对障碍物的避障,重现了真实行人在行走过程中可能表现出的各类现象。其结论如下: 1)改进的场域模型引入了决策点的概念,该决策点在遇到障碍物时能够引导行人进行转向,从而实现个体在障碍物前一定距离就采取绕行行为,从而还原出真人在躲避障碍物时产生的“避让三角区”和“收束三角区”现象。 2)在房间内不存在障碍物的情况下,行人与决策点之间不同的临界距离设置会导致虚拟人群在出口附近产生不同的形状,当临界距离赋值较低时,会在出口处产生成拱效应,而当赋值较高时,则会产生梯形现象。 3)通过设置一存在条形障碍物的走廊,行人通过障碍大致分为4个阶段:直线行走阶段、避让阶段、通过阶段和出口聚集阶段。在直线行走阶段人群组成的队列较为整齐,而在避让阶段行人采取绕行障碍行为,随后在出口处以相对固定的速度通过出口。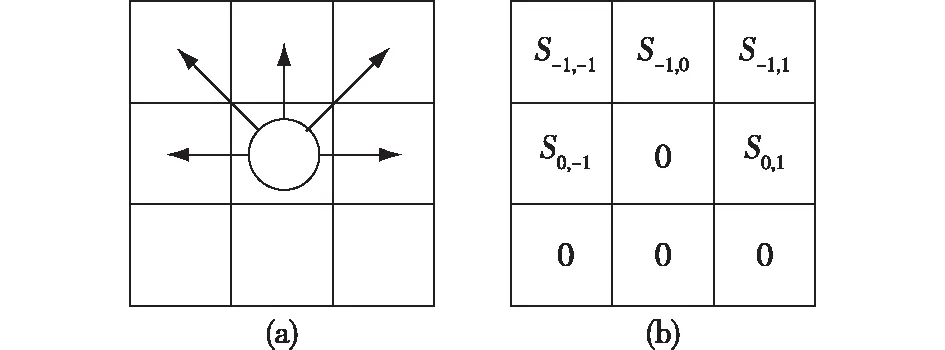
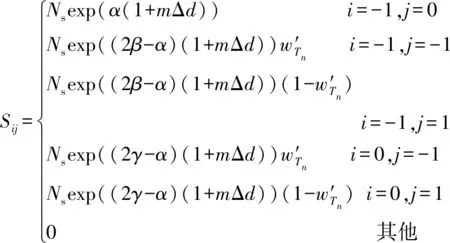
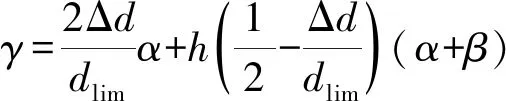
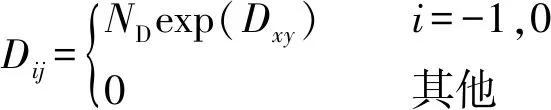
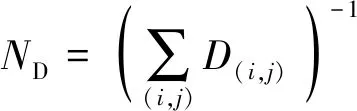
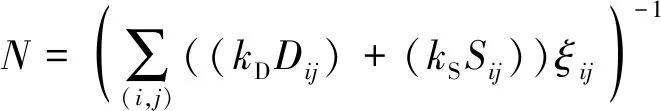
1.4 算法步骤
2 模型仿真
2.1 房间内不存在障碍物时的模拟仿真


2.2 房间内存在障碍物时的模拟仿真

2.3 模型运行结果
3 结论

