超长联高墩大跨矮塔斜拉桥主梁抗震性能研究

柯亮亮, 刘 亚, 苗建宝, 冯 威

(1.西安公路研究院有限公司, 西安 710065; 2.湖南大学, 长沙 410082)

中国地震频发,有接近一半的国土面积位于Ⅶ度以上的高烈度地区,其中大部分高烈度区位于中国西部山区[1]。高烈度地震严重威胁着桥梁运营安全和震后救灾的枢纽功能,因此,在桥梁设计过程必须考虑地震的影响。但目前我国桥梁抗震设计规范多侧重于中等高度桥墩的桥梁设计,而对高墩桥梁抗震规定较少。同时受限于地形地貌,高墩大跨桥梁的建设数量在西部高烈度山区占比越来越高,部分墩高达到200 m以上。已有研究表明,在强震作用下高墩大跨桥梁除了会出现传统中低墩桥梁常见的桥墩和主梁移位、落梁等震害外[2],在地震作用下主梁顶、底板和腹板也易出现开裂等病害[3-4]。因此,需进一步深化高墩大跨桥梁抗震性能研究。

目前,国内外学者多侧重于从桥墩出发对高墩大跨桥梁的抗震性能、破坏形态及设计方法[5-7]进行深入研究,而对主梁在地震作用下的响应规律研究较少[8]。胡思聪、吴少峰等[9-10]采用易损性的分析方法分别对高墩多塔斜拉桥和墩、梁固结的斜拉桥的抗震性能进行评估,指出主梁的失效概率较大,不能在高墩桥梁抗震设计中忽略主梁的损伤特性。童磊、岩下義弘等[3,5,11]分别对汶川地震中庙子坪大桥和熊本地震中阿苏长阳大桥的震害情况进行调研并指出,主梁开裂是高墩大跨刚构桥一大典型的震害形式。因此,探究高墩大跨桥梁主梁的地震响应规律非常重要。

另外,高墩大跨结构在地震作用下存在显著的P-Δ效应,若盲目忽视P-Δ效应的影响,则会导致结构抗震计算结果出现偏差,使得结构偏于不安全。各国学者对此进行了深入研究,但尚未达成共识。李睿等[12]基于高墩的反应谱分析结果,建议当墩高在20 m以上应考虑P-Δ效应的影响。魏斌等[13]建议,当稳定指标θΔ≤0.025即可忽略P-Δ效应的影响。Silva等[14]指出,当θΔ≤0.28时才可不计P-Δ效应的影响。以上研究侧重探讨了桥梁结构在抗震计算中是否考虑P-Δ效应的前提条件,但未将高墩P-Δ效应与高墩大跨桥梁易开裂的震害现象联系起来,即未探讨P-Δ效应对主梁地震响应的影响规律。与此同时,既有研究表明[15],行波效应对高墩大跨桥梁结构的内力影响也较为显著,应予以重视。

基于此,本文依托某高墩5跨矮塔斜拉桥实体工程,对比分析地震和活载作用下主梁的动力响应,并通过改变墩高,对比分析P-Δ效应对主梁地震响应的规律,在此基础上,引入行波效应,分析其对主梁地震动响应的影响。

1 依托工程及有限元建模

1.1 工程概况

依托工程为一座125 m+(4×230) m+125 m跨径的5塔6跨预应力混凝土刚构体系矮塔斜拉桥,联长达1 170 m,双向6车道,如图1所示。汽车活载采用公路-Ⅰ级,Ⅰ1类场地,特征周期为0.45 s,A类抗震设防,基本地震动峰值加速度为0.2g。

单位:m

1.2 建模及动力特性分析

采用Midas Civil建立依托工程的动力分析有限元模型,如图2所示。梁、塔、墩均采用空间梁单元模拟,斜拉索采用桁架单元模拟,墩、塔、梁固结,主梁在端部支座上仅可纵向滑动,墩底固结。进行动力分析时,改用脊梁模式对主梁进行仿真,并考虑相应质量惯性矩。

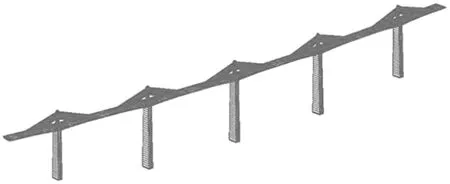
图2 有限元模型(阻尼比3%)

基于多重Ritz向量法对依托工程动力特性进行分析,其中,结构第1阶振型为纵飘,周期为6.84 s;结构第2阶振型为横向振动,周期为4.15 s,如图3所示。

(a) 1阶振型(f=0.146 Hz 纵向)

2 地震作用对主梁的影响

2.1 地震波的选取及移动荷载的考虑

对于地震作用,本文考虑地震波的纵、横、竖三向输入[16],选取依托工程场地地震安评报告中所给出的重现期为475年的3条地震波进行计算,如图4所示,并采用计算所得的最大值进行分析。另外,为了对比分析,结合依托工程场地特征,选取常用的Taft波和EI Centro波,并将其NS向、EW向和UP向分别调幅至0.2g、0.2g和0.14g后输入模型,进行非线性时程分析。

对于车辆移动荷载,根据规范[16]规定与依托工程实际的车道数、计算跨径采用活载综合系数进行考虑。横、纵向折减系数分别取0.55和0.97,横向偏载系数取1.15,计算得到活载综合系数为3.68。

2.2 主梁内力对比

主梁分别在地震和活载作用下的内力包络图如图5所示。部分典型截面中(即图1中截面A、B、C、D)安评波与活载峰值响应结果如表1所示。

(a) 纵向弯矩

从表1结果可见,总的来说,大跨高墩桥梁主梁在地震作用下内力响应基本都大于活载效应,其中主梁在安评波作用下,边墩梁结合处的纵向弯矩和剪力响应值远大于活载效应值,分别为后者的12.46倍和4.61倍。

另外,由于地震波的不确定性,主梁在不同地震波的作用下峰值响应会有所差别,但趋势一致,其中主梁纵向弯矩和剪力表现为在墩梁结合处最大,跨中最小,而主梁横向弯矩表现为在中间墩(12#墩)的墩梁结合处最大,故在高烈度区的大跨高墩刚构或矮塔斜拉桥的设计过程中,应重点关注墩梁结合处的受力情况。

2.3 主梁应力对比

主梁分别在安评波和活载作用下的应力值对比情况如图6和表2所示。

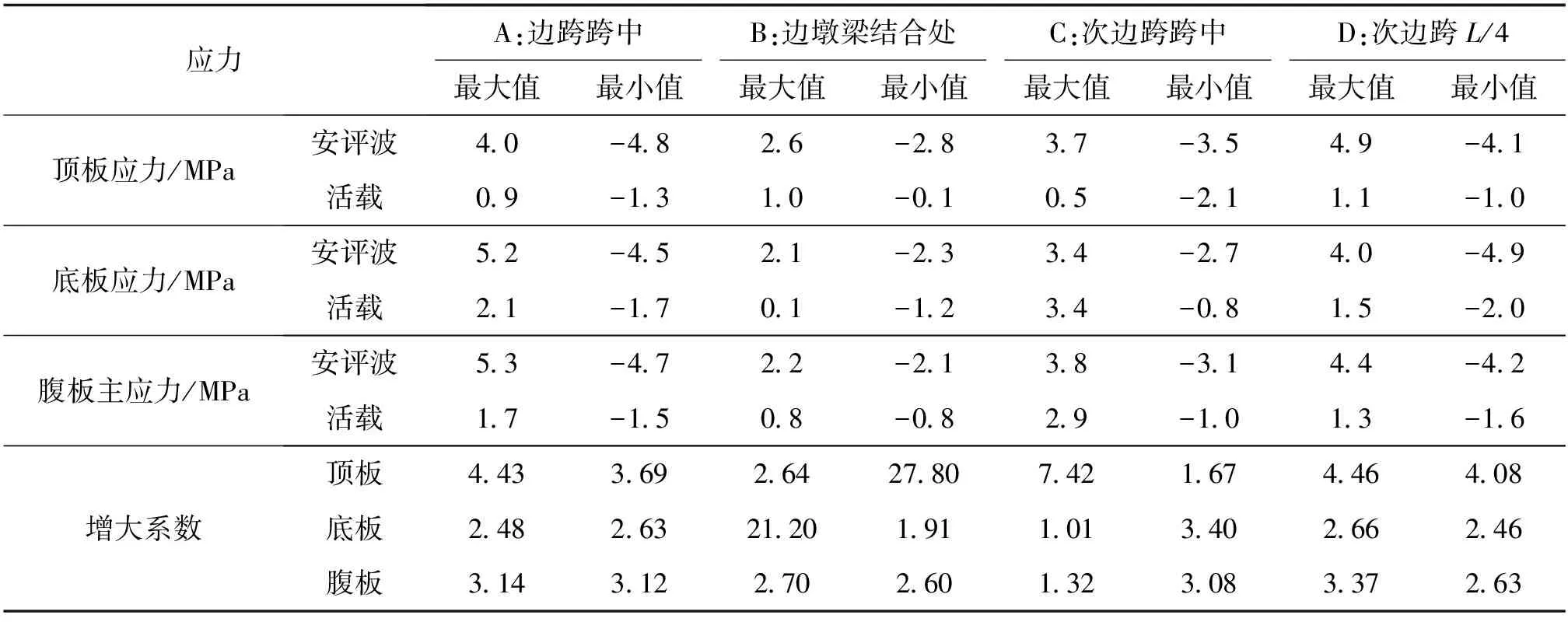
表2 主梁应力峰值

(a) 顶板

由图6和表2可知,与前述分析结果相似,相较活载作用,地震作用对主梁截面各部分应力的影响更大,主梁各部分应力的活载效应包络基本都位于地震响应包络之内。

值得注意的是,在地震激励下,主梁边跨1/3～1/2、次边跨和中跨1/4～3/4区域主拉应力较,且箱梁腹板和底板应力响应大于顶板,其中,腹板和底板的最大主拉应力值分别达到了6.6 MPa和6.5 MPa,且最小主拉应力为2.0 MPa,远超活载效应。这也表明,在地震作用下,大跨高墩桥梁主梁腹板和底板存在较大的开裂风险,与庙子坪特大桥在汶川地震中的主梁实际裂缝震害情况相吻合[3]。

既有研究表明,常规桥梁的主梁在地震作用下基本处于弹性阶段,通常以车辆荷载作为主要可变作用控制主梁设计,而综合大跨高墩桥梁主梁分别在地震作用和活载作用的内力及应力特点可以发现,与常规桥梁不同,地震作用对大跨高墩桥梁结构的影响显著且大于活载效应。因此,主梁设计时,应考虑地震作用。

3 高墩P-Δ效应

高墩结构由于长细比、轴压比较大,P-Δ效应显著,在地震作用下会加剧主梁的开裂风险。为此,需分析静力及动力P-Δ效应的影响,如图7所示。

(a) 静力二阶效应

3.1 静力P-Δ效应

静力二阶效应如图7(a)所示。线弹性单自由度体系在静力作用下不考虑P-Δ效应时,动力方程可表示为:

F=KΔ

(1)

考虑P-Δ效应时,静力方程可表示为:

(2)

(3)

式中:F为墩顶水平力;K为墩柱抗推刚度;P为墩顶竖向力;H为墩高;Δ为不考虑P-Δ效应时墩顶的侧向位移;Δ1为考虑P-Δ效应时墩顶的侧向位移;θ为衡量P-Δ效应指标的静力稳定系数。

式(2)可改写为:

(4)

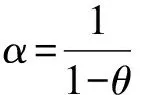
静力作用下,P-Δ效应会增大结构的弯矩和位移,且P-Δ效应的影响随静力稳定系数的增大而增大。

3.2 动力P-Δ效应

动力二阶效应如图7(b)所示。线弹性单自由度体系在地震作用下考虑P-Δ效应后,动力方程可表示为:

(5)

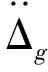
由式(5)可知,单自由度体系考虑P-Δ效应后的地震响应相当于期刚度折减为K/α后的一阶响应。假设不考虑P-Δ效应时,结构周期为T0,则考虑P-Δ效应后结构周期为:

(6)

若Sd0和Sdi分别为位移谱上周期T0和Ti对应的幅值,则地震作用下考虑P-Δ效应后结构水平位移增大系数为:

(7)

考虑P-Δ效应使结构刚度降低,也会改变结构周期,使其地震响应也随之变化。当结构周期由T0变为T1时,结构位移响应增大,此时αe>1;当结构周期由T0变为T2时,相应地降低了地震能量输入,考虑P-Δ效应使得结构位移减小,此时αe<1,如图7(b)所示。因此,可初步判断P-Δ效应由结构动力特性和地震波频谱特性综合决定。

3.3 P-Δ效应对主梁地震响应的影响

在上述动力有限元分析模型的基础上,通过将桥墩高度调整为60 m、80 m、100 m、120 m及140 m,旨在研究水平地震作用下不同P-Δ效应对高墩大跨桥梁的影响,同时考虑到地震的不确定性,选取5条代表性地震波,如表3所示,统一调幅至0.2g后沿纵桥向输入有限元模型中进行非线性时程分析。

表3 地震波

本文从结构基本周期、位移和内力3个角度探讨P-Δ效应的影响。其中,各条地震波位移谱与不同墩高下依托工程基本周期的对应关系如图8所示。不同地震波下P-Δ效应对梁端位移的影响和相同地震波下P-Δ效应对主梁关键截面纵向弯矩的影响如图9、图10所示。

图8 不同地震波下位移反应谱

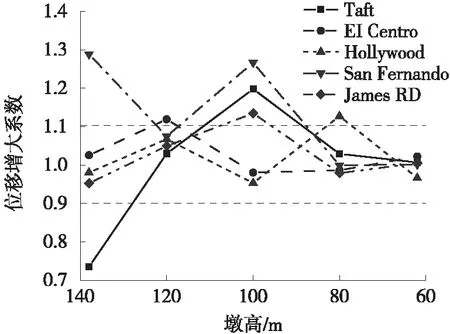
图9 梁端纵向位移增大系数

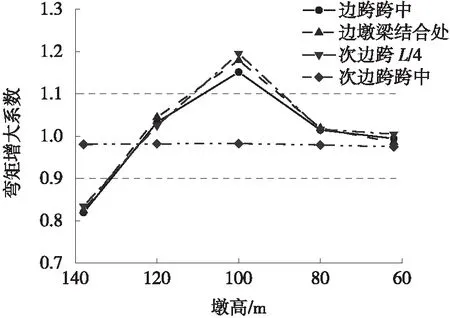
图10 Taft波作用下主梁纵向弯矩增大系数

由图8可知,考虑P-Δ效应会使得结构基本周期增加。由图9可知,在同一地震波下,P-Δ效应对不同墩高桥梁的梁端位移影响各不相同,如在Taft波作用下,140 m墩高桥梁在考虑P-Δ效应后,梁端位移减少了26%,但当墩高在100 m时,反而增加了20%。其次,在不同地震波下,P-Δ效应对相同墩高桥梁的梁端位移影响也不尽相同,墩高为140 m时,San Fernando波作用下的P-Δ效应使得梁端位移增加了29%。当墩高在80 m及以下时,考虑P-Δ效应后对梁端位移影响较小,基本处于10%以内。

由图10可知,在相同地震波作用下,主梁次边跨跨中截面的纵向弯矩对P-Δ效应较为不敏感,而边跨跨中、边墩梁结合处及次边跨L/4处纵向弯矩对P-Δ效应相对更为敏感,且随着墩高的降低,弯矩的变化规律与梁端位移的变化规律相似。

综合图8～图10可知,出现以上现象的原因,由于墩高越高,P-Δ效应也越明显,对结构基本周期的影响也越大,因此也就造成了当墩高在80 m及以下时,对结构地震动响应影响较低,考虑P-Δ效应的影响基本位于±10%以内,此时结构基本周期变化小于2%。另外,当考虑P-Δ效应后,使得结构基本周期的变化位于地震波位移谱增长阶段时(如桥墩采用80 m时的Hollywood波中),P-Δ效应表现为放大结构地震动响应的作用,反之,当结构基本周期变化位于地震波位移谱下降阶段时(如桥墩采用140 m时的Taft波中),P-Δ效应对结构地震动响应具有减小作用。

综上所述,P-Δ效应通过影响结构的动力特性影响其地震动响应,此类影响对结构是否有利与地震波的频谱特性密切相关。因此,建议当同时满足以下2个条件时,需考虑P-Δ效应对主梁的不利影响:1) 当考虑P-Δ效应使得结构基本周期变化超过2%,即结构静力稳定系数大于0.04;2) 考虑P-Δ效应时结构基本周期变化位于地震波位移谱剧烈增长阶段或卓越周期内。

4 行波效应对主梁的影响

地震波时空运动过程差异显著,在中小跨径桥梁抗震分析中,一般仅计入到达时间的差异,未计入空间的变化特性。即假设各支点的运动相同,但因地震波到达地面观测点的时间不同,导致观测点地震波有相位差,从而引起其地震响应完全不同或差异很大。因此,在对大跨径桥梁开展时程分析时需考虑行波效应。

4.1 关键截面及行波效应的考虑

在考虑行波效应影响下,对高墩大跨斜拉桥主梁地震响应分析时,须重点关注行波效应对主梁各跨跨中竖向位移、主梁各跨跨中及各墩梁结合处内力响应的影响。因此,选取主梁各跨跨中及墩梁结合处截面为关键截面。

地震波运动方向由9#墩向15#墩运动。视波速v根据我国对场地类别剪切波速的规定,分别取为100 m/s、200 m/s、400 m/s、800 m/s、1 600 m/s和无穷大(即一致激励)时高墩大跨斜拉桥模型的地震响应。根据本文方案桥跨径布置,得到底地震波到达各个墩的时间,如表4所示。

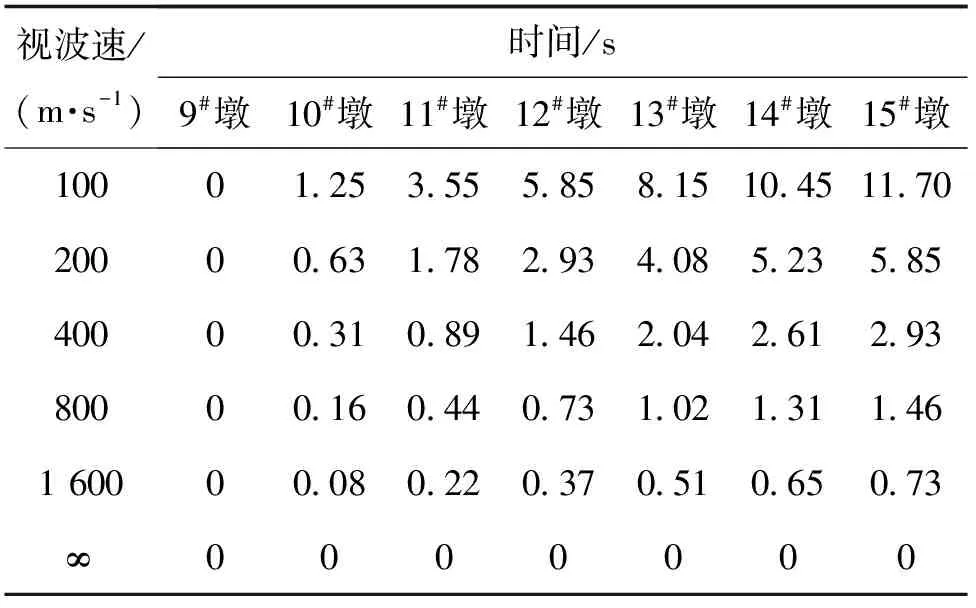
表4 地震波到达各个墩底时间

4.2 分析结果

基于大量非线性有限元分析及考虑行波效应后,不同视波速下主梁跨中竖向位移峰值结果如图11所示,跨中和各墩梁结合处内力峰值结果如图12所示。

(a) 位移

(a) 剪力

由图11(a)可知,考虑行波效应后,主梁次边跨和中跨跨中竖向位移随视波速的减小呈增大趋势。当视波速为100 m/s时,中跨跨中竖向位移达160 mm,与一致激励相比,主梁各跨跨中竖向位移分别增大了0.6、2.8、1.9、2.9、3.1、1.3倍,原因在于行波效应引起了结构对称振型的参与。因此,需特别关注计入行波效应影响下主梁跨中竖向位移的变化情况。

由图12(a)可知,当视波速大于800 m/s时,行波效应对梁墩结合处主梁剪力响应影响较小,且随着视波速的增大,该处剪力趋于一致激励作用下的响应。当视波速小于800 m/s时,墩梁结合处主梁剪力随视波速的减小先减小后增大,且当视波速为200 m/s时,12#中墩梁结合处剪力减小程度最明显,减幅达60%,但随着视波速进一步减少至100 m/s时,其剪力又呈增大趋势。因此,当视波速大于200 m/s时,可忽略行波效应引起的墩梁结合处主梁剪力变化,但当视波速进一步减少时,墩梁结合处主梁剪力反而会随之增大。

由图11(b)和图12(b)可知,随着地震波视波速的减小,主梁跨中弯矩可能增大也可能减小,其中边跨跨中弯矩先减小后增大,且均小于一致激励响应。次边跨及中跨弯矩可能大于一致激励响应,如视波速为800 m/s和100 m/s时,次边跨跨中弯矩均比一致激励下增大了1.2倍;同样,墩梁结合处主梁弯矩随视波速的减小可能增大也可能减少,如当视波速为800 m/s时,10#、11#及14#墩梁结合处主梁弯矩比一致激励作用下均增大了1.1倍。因此,需关注行波效应引起的主梁弯矩响应的变化。

综上所述,行波效应作用可能会导致高墩大跨桥梁主梁地震动响应结果的改变,且随视波速的减小,其影响越大,可致使部分截面处于偏不安全的状态。

5 结论

1) 与常规桥梁不同,地震作用对大跨高墩桥梁结构主梁的影响显著大于活载效应,应考虑地震作用组合效应控制主梁设计。

2)P-Δ效应通过影响结构的动力特性来影响其地震动响应,此类影响对结构是否有利,与地震波的频谱特性密切相关。建议当考虑P-Δ效应使得结构基本周期变化超过2%,且变化位于地震波位移谱剧烈增长阶段或卓越周期内,需在该类桥梁抗震设计中考虑P-Δ效应的影响。

3) 计入行波效应作用可能会显著增大主梁跨中竖向位移弯矩,且视波速越小影响越大,忽略行波效应的影响可能导致主梁处于危险状态,主梁抗震设计时需注意其影响。