利用“微柱元法”处理流体问题的常见困惑探讨
石 睿
(福州第一中学 福建 福州 350000)
在动量定理的应用中,流体问题是常见的一类问题,而在讲解这类问题时,教师多选择“微柱元法”来帮助学生将流体转化为熟悉的质点模型(图1):在源源不断的流体中截取一小段柱体作为研究对象,先表示出该柱元的质量Δm,再利用动量定理将速度变化量Δv与力F联系起来.

图1 微柱元法
1 “微柱元法”的常规解法
【例1】(多选)如图2所示,直-20武装直升机的旋翼桨盘面积(桨叶旋转形成的圆面面积)为S,空气密度为ρ,直升机质量为m,重力加速度为g.当直升机悬停在空中时,空气浮力不计,风力的影响也不计,下列说法正确的是( )

图2 例1题图
A.直升机悬停时受到的升力大小为mg
答案:A、C.
解析:对直升机进行受力分析,如图3所示.
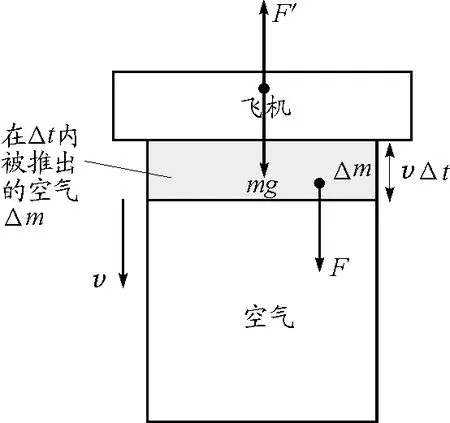
图3 “微柱元法”分析
由平衡条件得
F′=mg
对极短时间Δt内被推出的空气Δm有
F=F′=mg
Δm=ρV=ρSvΔt
FΔt=Δm(v-0)
因此
1 s内被推动的空气质量
1 s内发动机做的功,即发动机的功率为
2 “微柱元法”常见困惑探讨
但在细究之下,水平较高的学生又产生如下一些疑惑.
困惑1:在Δt内被推出的空气Δm由零加速至v,为何可以用vΔt表示这块空气在Δt内通过的距离?
这可以从理想流体的定常流动上理解.理想流体的流动可看作定常流动,即流体中任一点的流速、通过任意截面的流量不随时间变化.
在Δt内通过截面S1、S2的空气质量相同(图4),即在Δt内从飞机被加速至v的空气Δm与以稳定速度v在Δt内通过S2的空气质量Δm′相等.即

图4 理想流体的定常流动分析
Δm=Δm′=ρV=ρSvΔt
困惑2:1 s内发动机做的功,即发动机提供推力的功率,为何从P=Fv的角度得到的结果与正确答案不同?
错解
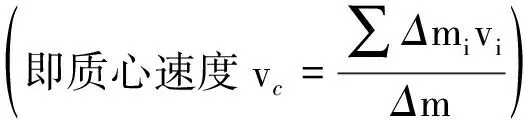
即
解析中
这两种解法的区别还在于研究过程的不同,前者是对直升机悬停时的任一个瞬间分析,而后者是对单位时间内喷射出的气体m1的加速过程分析.
困惑3:时间间隔Δt不取极短可以吗?即一定要使用微柱元法吗?
在本题的解析中,是否Δt→0,并没有影响.但在非连续流体及较重流体问题中利用微柱元法可以辨别清楚流体与固体的相互作用过程.
【例2】为估算池中睡莲叶面承受雨滴撞击产生的平均压强,小明在雨天将一圆柱形水杯置于露台,测得1 h内杯中水上升了45 mm.查询得知,当时雨滴竖直下落速度约为12 m/s.据此估算该压强约为(设雨滴撞击睡莲后无反弹,不计雨滴重力,雨水的密度为1×103kg/m3)( )
A.0.15 Pa B.0.54 Pa
C.1.5 Pa D.5.4 Pa
答案:A.
解析:对极短时间Δt到达莲叶上的雨水Δm为
(1)
(注意由于是非连续流体Δm≠ρSvΔt)
-FΔt=Δm(0-v)
(2)
(3)
由式(1)~(3),得
为何在式(2)中不用考虑雨水重力的冲量?由于Δt→0,IG=ΔmgΔt为二阶小量,IG=ΔmgΔt≪|Δp|=Δm(v-0),可以忽略不计.
若研究过程选取t=1 h,会有什么区别?在时间t内到达莲叶的雨水质量:m=ρSh.在时间t内作用在m上的重力冲量IG与m撞击莲叶的动量变化量大小|Δp|之比为
即IG≫|Δp|,那么IG不可忽略?即
-Ft+mgt=m(0-v)
仔细辨别一下这个研究过程会发现:虽然在t=1 h内,共有质量为m的雨滴掉落在莲叶上,但m并不是同时掉落在莲叶上,IG=mgt中的m应为每个瞬间Δt掉落的Δm(Δt→0,Δm→0),故
IG=Δmgt≪|Δp|
可以忽略.即
-Ft=m(0-v)
(4)
由于在每个瞬间Δt内只有一小段雨水微元Δm与莲叶相接触,故即使对全过程t=1 h列式(4),其实是对各个Δt中式(2)叠加的结果,也用到了微柱元法的思想.微柱元法相较于全程法,更加贴近流体问题中相互作用的本质,更容易避开误区.
3 总结
在处理流体问题时,先通过“微柱元法”建立起熟悉的质点模型,再通过对相互作用过程的理解与分析选择正确的定理定律解决问题.以上3个思维困惑的探讨,虽然解答各不相同,但其实都围绕着一个主题:研究对象和研究过程的选择.准确清晰地选好研究对象与研究过程是物理问题探讨的基础,也是学生基本物理素养的体现.

